图论--最短路问题
图论–最短路问题
邻接表
/*
e[idx]:存储点的编号
w[idx]:存储边的距离(权重)
*/
void add(int a, int b, int c) {e[idx] = b;ne[idx] = h[a];w[idx] = ch[a] = idx ++;
}
1.拓扑排序
给定一个 n 个点 m 条边的有向图,点的编号是 11 到 n,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 −1−1。
若一个由图中所有点构成的序列 A 满足:对于图中的每条边 (x,y),x在 A中都出现在 y 之前,则称 A是该图的一个拓扑序列。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 x 和 y,表示存在一条从点 x 到点 y的有向边 (x,y)。
输出格式
共一行,如果存在拓扑序列,则输出任意一个合法的拓扑序列即可。
否则输出 −1−1。
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>using namespace std;const int N = 1e5 + 10;int n, m;// 队列
int q[N], hh, tt = -1;// 邻接表
int e[N], idx, ne[N], h[N];// 入度
int d[N];void add(int a, int b) {e[idx] = b;ne[idx] = h[a];h[a] = idx ++;
}bool topsort() {for (int i = 1; i <= n; i ++)if (!d[i])q[++ tt] = i;while (hh <= tt) {int tmp = q[hh ++];for (int i = h[tmp]; i != -1; i = ne[i]) {int j = e[i];d[j] --;if (!d[j])q[++ tt] = j;}}if (tt == n-1) return true;return false;
}int main() {memset(h, -1, sizeof h);cin >> n >> m;while (m --) {int a, b;cin >> a >> b;add(a, b);d[b] ++;}if (topsort()) for (int i = 0; i < n; i ++)cout << q[i] << ' ';else cout << -1;return 0;
}
2.Dijkstra求最短路
稠密图(边很多)——邻接矩阵
所有边权都是正数,单源最短路
-
初始化到每个节点距离为无穷inf,初识节点距离dist[1] = 0
-
迭代n轮
-
每次从未标记的节点中选择距离出发点最近的节点,标记,收录到最优路径集合中
-
计算刚加入节点A的临近节点B的距离(不包含标记的节点)。若节点A的距离加节点A到B的距离小于节点B的距离,则更新节点B的距离。
给定一个 n 个点 m条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>using namespace std;const int N = 505;int n, m;// 标记
int st[N];
// 距离
int dist[N];
// 邻接矩阵
int g[N][N];int dijkstra() {memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < n; i ++) {int t = -1;// 选择距离出发点最近的节点for (int j = 1; j <= n; j ++) if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;st[t] = 1;for (int j = 1; j <= n; j ++) dist[j] = min(dist[j], dist[t] + g[t][j]);}if (dist[n] == 0x3f3f3f3f)return -1;return dist[n];
}int main() {memset(g, 0x3f, sizeof g);scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++)g[i][i] = 0;while (m --) {int x, y, z;scanf("%d%d%d", &x, &y, &z);g[x][y] = min(g[x][y], z);}int ans = dijkstra();printf("%d", ans);return 0;
}
堆优化
稀疏图(点很多)——邻接表
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cstdio>using namespace std;typedef pair<int, int> pii;const int N = 1e6 + 10;int n, m;// 标记,避免自环
int st[N]; // 邻接表
int e[N], h[N], ne[N], w[N], idx;void add(int a, int b, int c) {e[idx] = b;ne[idx] = h[a];w[idx] = c;h[a] = idx ++;
}int dist[N];int dijkstra() {memset(dist, 0x3f, sizeof dist);dist[1] = 0;// 小根堆 {边权(距离),编号}priority_queue<pii, vector<pii>, greater<pii>> heap;heap.push({0, 1});while (!heap.empty()) {int v = heap.top().second, distance = heap.top().first;heap.pop();if (st[v]) continue;st[v] = 1;for (int i = h[v]; i != -1; i = ne[i]) if (dist[e[i]] > dist[v] + w[i]){dist[e[i]] = dist[v] + w[i];heap.push({dist[e[i]], e[i]});}}if (dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}int main() {memset(h, -1, sizeof h);scanf("%d%d", &n, &m);while (m --) {int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}int t = dijkstra();printf("%d", t);return 0;
}3.Bellman-Ford算法(存在负权边,有边数限制最短路)
有负权回路,最短路不一定存在
for k 次
for 所有边 a, b, w
松弛操作:dist[b] =min(dist[b,dist[a]+w)
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出从 1号点到 n 号点的最多经过 k 条边的最短距离,如果无法从 1 号点走到 n 号点,输出
impossible。注意:图中可能 存在负权回路 。
#include <cstdio>
#include <cstring>
#include <iostream>using namespace std;int dist[505], backup[505];
int n, m, k;struct edge {int a, b, w;
} edges[10010];void bellman_ford() {memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < k; i ++) {memcpy(backup, dist, sizeof dist);for (int i = 0; i < m; i ++) {int a = edges[i].a, b = edges[i].b, w = edges[i].w;dist[b] = min(dist[b], w + backup[a]);}}}int main() {scanf("%d%d%d", &n, &m, &k);for (int i = 0; i < m; i ++) {int a, b, c;scanf("%d%d%d", &a, &b, &c);edges[i] = {a, b, c};}bellman_ford();if (dist[n] > 0x3f3f3f3f / 2) puts("impossible");else printf("%d", dist[n]);return 0;
}
4.SPFA算法(与负权边,无负权回路)
给定一个 n个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出 1号点到 n 号点的最短距离,如果无法从 11 号点走到 n 号点,则输出
impossible。数据保证不存在负权回路。
#include <iostream>
#include <cstring>
#include <queue>using namespace std;const int N = 1e5 + 10;int idx, h[N], ne[N], e[N], w[N];int n, m;// 判断该点是否在队列
bool st[N];
int dist[N];void add(int a, int b, int c) {e[idx] = b;ne[idx] = h[a];w[idx] = c;h[a] = idx ++;
}int spfa() {memset(dist, 0x3f, sizeof dist);dist[1] = 0;queue<int> q;q.emplace(1);st[1] = 1;while (!q.empty()) {int t = q.front();q.pop();st[t] = 0;for (int i = h[t]; i != -1; i = ne[i]) {if (dist[e[i]] > dist[t] + w[i]) {dist[e[i]] = dist[t] + w[i];if (!st[e[i]]) {q.emplace(e[i]);st[e[i]] = 1;}}}}return dist[n];
}int main() {ios::sync_with_stdio(false);memset(h, -1, sizeof h);cin >> n >> m;while (m--) {int a, b, c;cin >> a >> b >> c;add(a, b, c);}int t = spfa();if (t == 0x3f3f3f3f) cout << "impossible" << endl;else cout << t;return 0;}
5.Floyd求在求最短路(多源)
给定一个 n 个点 m条边的有向图,图中可能存在重边和自环,边权可能为负数。
再给定 k 个询问,每个询问包含两个整数 x 和 y,表示查询从点 x 到点 y 的最短距离,如果路径不存在,则输出
impossible。数据保证图中不存在负权回路。
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 210, inf = 1e9;int d[N][N];int n;void floyd() {for (int k = 1; k <= n; ++k) {for (int i = 1; i <= n; ++i)for (int j = 1; j <= n; ++j) d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}
}int main() {int m, k;cin >> n >> m >> k;for (int i = 1; i <= n; ++i)for (int j = 1; j <= n; ++j) {if (i == j) d[i][j] = 0;else d[i][j] = inf;}while (m--) {int a, b, c;cin >> a >> b >> c;d[a][b] = min(d[a][b], c);}floyd();while (k--) {int a, b;cin >> a >> b;if (d[a][b] > inf / 2) puts("impossible");else cout << d[a][b]<<endl;}return 0;
}
相关文章:

图论--最短路问题
图论–最短路问题 邻接表 /* e[idx]:存储点的编号 w[idx]:存储边的距离(权重) */ void add(int a, int b, int c) {e[idx] b;ne[idx] h[a];w[idx] ch[a] idx ; }1.拓扑排序 给定一个 n 个点 m 条边的有向图,点的编号是 11 到 n…...
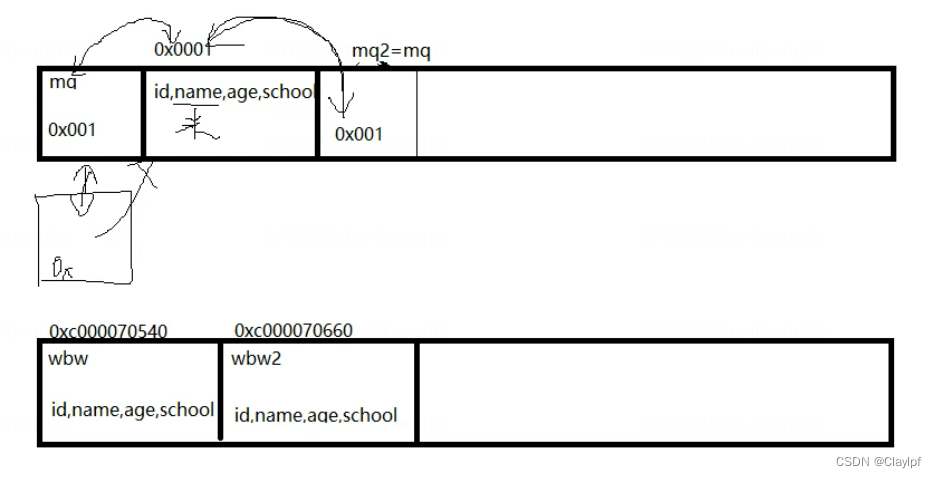
go 结构体 - 值类型、引用类型 - 结构体转json类型 - 指针类型的种类 - 结构体方法 - 继承 - 多态(interface接口) - 练习
目录 一、结构体 1、python 与 go面向对象的实现: 2、初用GO中的结构体:(实例化一个值类型的数据(结构体)) 输出结果不同的三种方式 3、实例化一个引用类型的数据(结构体) 4、…...

盘点16个.Net开源项目
今天一起盘点下,16个.Net开源项目,有博客、商城、WPF和WinForm控件、企业框架等。(点击标题,查看详情) 一、一套包含16个开源WPF组件的套件 项目简介 这是基于WPF开发的,为开发人员提供了一组方便使用自…...
记录对 require.js 的理解
目录 一、使用 require.js 主要是为了解决这两个问题二、require.js 的加载三、main.js 一、使用 require.js 主要是为了解决这两个问题 实现 js 文件的异步加载,避免网页失去响应;管理模块之间的依赖性,便于代码的编写和维护。 二、require.…...
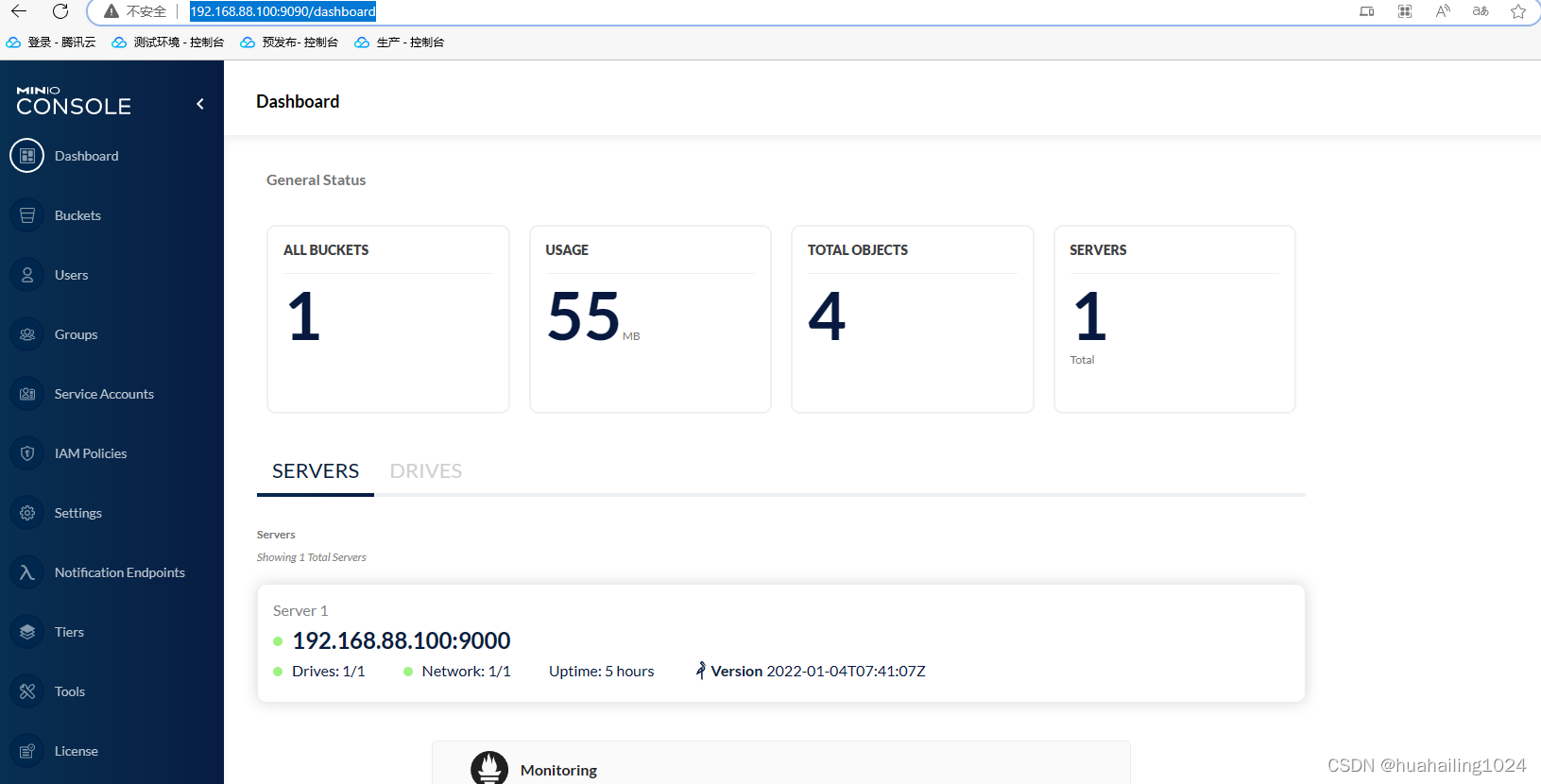
minio-分布式文件存储系统
minio-分布式文件存储系统 minio的简介 MinIO基于Apache License v2.0开源协议的对象存储服务,可以做为云存储的解决方案用来保存海量的图片,视频,文档。由于采用Golang实现,服务端可以工作在Windows,Linux, OS X和FreeBSD上。配置…...
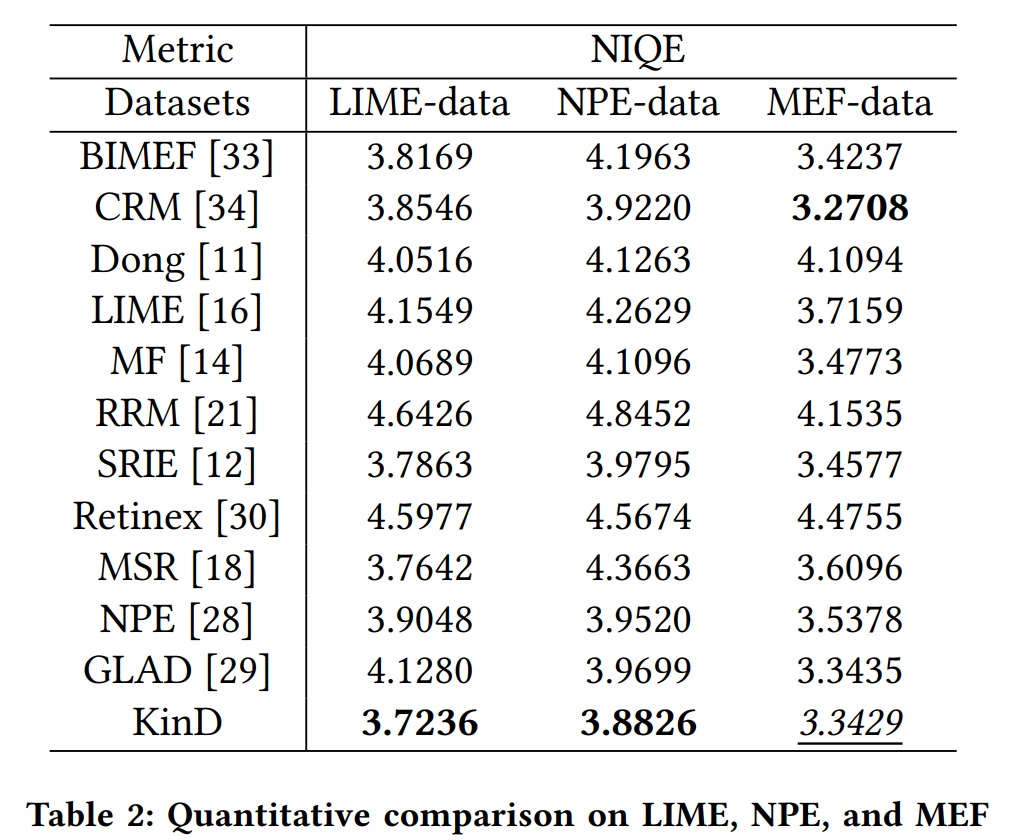
Kindling the Darkness: A Practical Low-light Image Enhancer论文阅读笔记
这是ACMMM2019的一篇有监督暗图增强的论文,KinD其网络结构如下图所示: 首先是一个分解网络分解出R和L分量,然后有Restoration-Net和Adjustment-Net分别去对R分量和L分量进一步处理,最终将处理好的R分量和L分量融合回去。这倒是很常…...

AcWing 4575. Bi数和Phi数
文章目录 题意:思路:代码 题意: 就是给你n个数,对于每一个数y你都需要找到一个最小x使得 ϕ ( x ) ≥ y \phi(x) \ge y ϕ(x)≥y,然后再求一个最小平和。 思路: 其实最开始以来的思路就是二分,我先进行线性筛求出每个数的欧拉函数…...
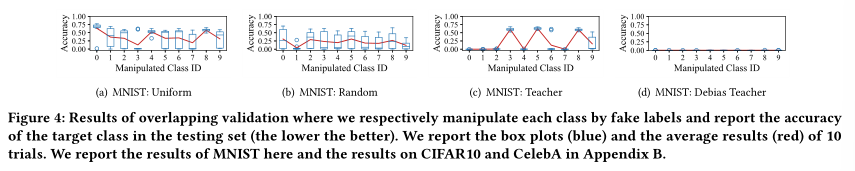
《Federated Unlearning via Active Forgetting》论文精读
文章目录 1、概述2、方法实验主要贡献框架概述 3、实验结果比较方法实验结果忘却完整性忘却效率模型实用性 4、总结 原文链接: Federated Unlearning via Active Forgetting 1、概述 对机器学习模型隐私的⽇益关注催化了对机器学习的探索,即消除训练数…...
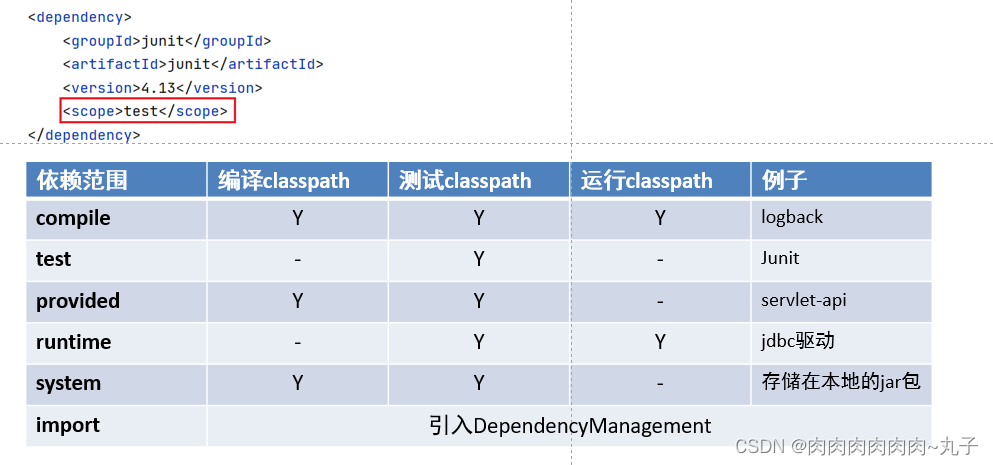
Java课题笔记~Maven基础知识
一、什么是Maven? Maven是专门用于管理和构建Java项目的工具。 它的主要功能有: 提供了一套标准化的项目结构提供了一套标准化的构建流程(编译,测试,打包,发布……)提供了一套依赖管理机制 …...
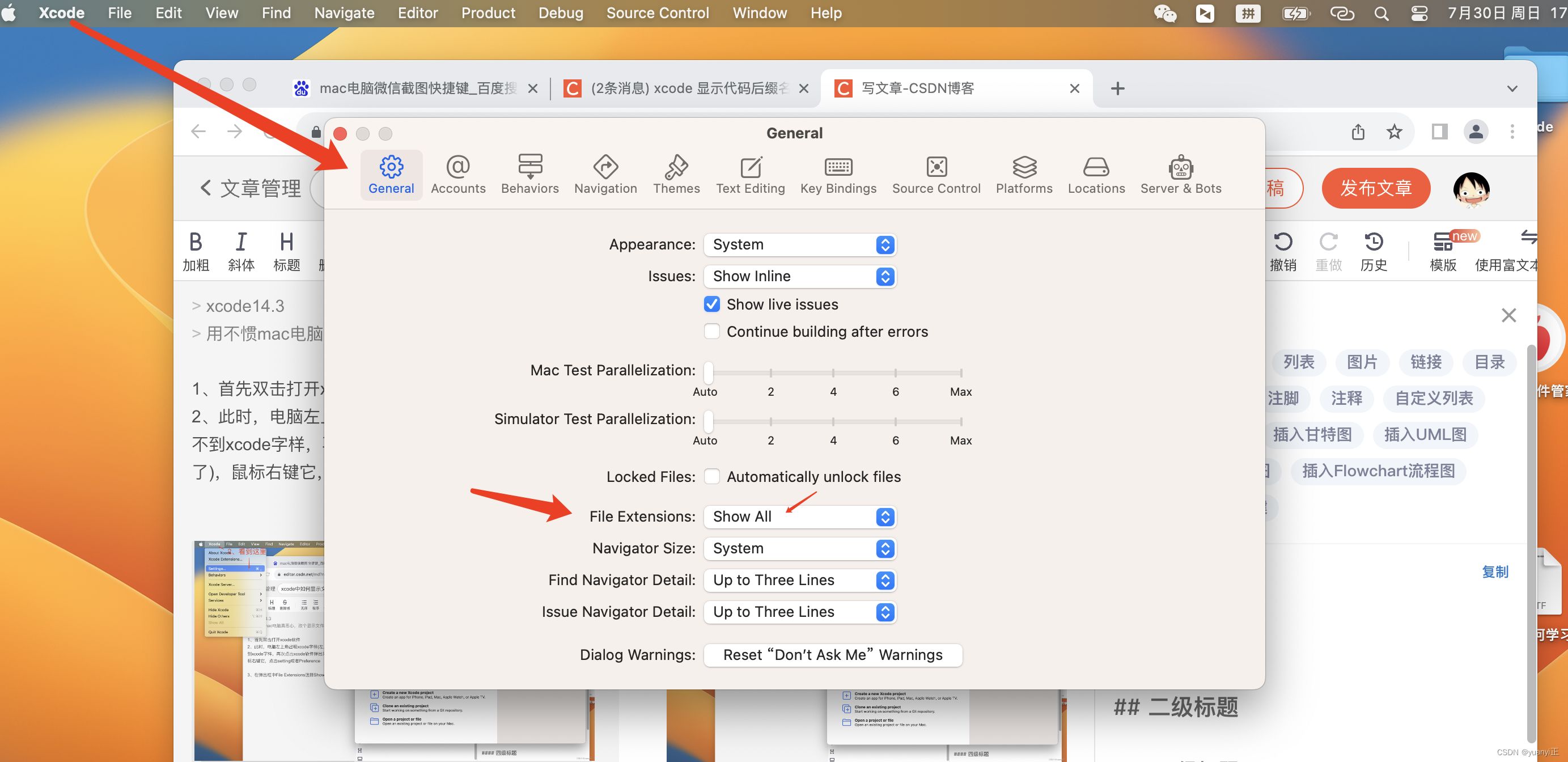
xcode中如何显示文件后缀
xcode14.3 用不惯mac电脑真恶心,改个显示文件后缀找半天 1、首先双击打开xcode软件 2、此时,电脑左上角出现xcode字样(左上角如果看不到xcode字样,再次点击xcode软件弹出来就有了),鼠标右键它,点击setting或者Prefere…...

SpringBoot使用JKS或PKCS12证书实现https
SpringBoot使用JKS或PKCS12证书实现https 生成JKS类型的证书 可以利用jdk自带的keytool工具来生成证书文件, 默认生成的是JKS证书 cmd命令如下: 执行如下命令,并按提示填写证书内容,最后会生成server.keystore文件 keytool -genkey tomcat…...
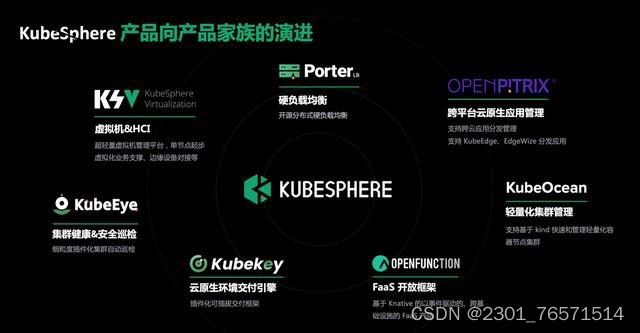
云原生势不可挡,如何跳离云原生深水区?
云原生是云计算领域一大热词,伴随云原生概念而来的是数字产业迎来井喷、数字变革来临、数字化得以破局以及新一波的技术红利等等。云原生即“云”原生,顾名思义是让“应用”最大程度地利用云的能力,发挥云价值的最佳路径。具体来说࿰…...
python的decimal或者叫Decimal,BigDecimal
前言 在python中进行小数计算时,很容易发生精度错误问题!!!!一定要注意!!!或者说,只要进行小数的运算都要用decimal。如:银企对账;工程计算等等在…...

Mac环境变量问题
查询环境变量 echo $PATH 查询当前使用的Shell,这里注意SHELL需要大写 echo $SHELL >>>如果输出的是/bin/zsh,说明使用的是zsh。zsh读取的个人配置文件是~/.zshrc (mac10.15.x 后对应的是~/.zprofile) >>>如果输出的是/bin/bash&…...

Shell脚本学习-Web服务监控
参考我的博客文章《Centos安装nginx》,先来安装下nginx。我按照该文档操作了一遍,还是很快就能安装好nginx的。 确认可以安装成功: [rootvm1 sbin]# netstat -atunlp |grep 80 tcp 0 0 0.0.0.0:80 0.0.0.0:* …...
【ChatGPT】基于WSL+Docker的ChatGPT PLUS共享服务部署
最近买了ChatGPT PLUS服务,想通过web服务将它共享给其他人使用,搜了一下目前GitHub上比较热门的服务有 ChatGPT-Next-Webchatgpt-web-share 其中chatgpt-web-share支持API和PLUS账号分享两种方式,且架构为PythonJSDocker,相对比…...
【论文阅读24】Better Few-Shot Text Classification with Pre-trained Language Model
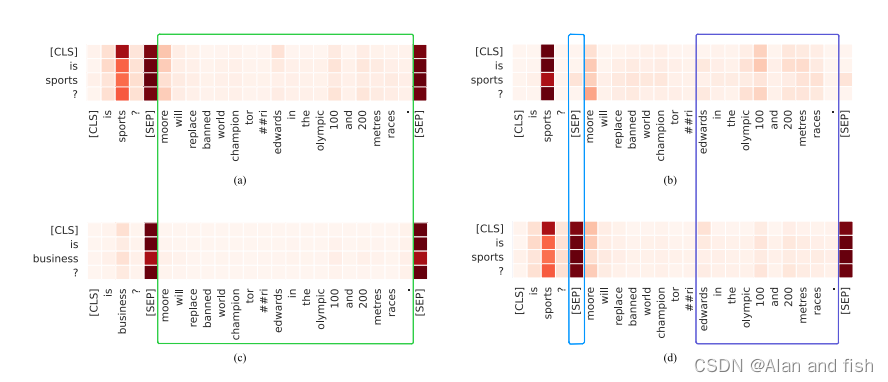
论文相关 论文标题:Label prompt for multi-label text classification(基于预训练模型对少样本进行文本分类) 发表时间:2021 领域:多标签文本分类 发表期刊:ICANN(顶级会议) 相关代…...
)
119、Spring容器启动流程是怎样的(配有Spring启动完整流程图)
Spring容器启动流程是怎样的 在创建Spring容器,也就是启动Spring时:首先会进行扫描,扫描得到所有的BeanDefinition对象,并存在一个Map中然后筛选出非懒加载的单例BeanDefinition进行创建Bean,对于多例Bean不需要在启动…...
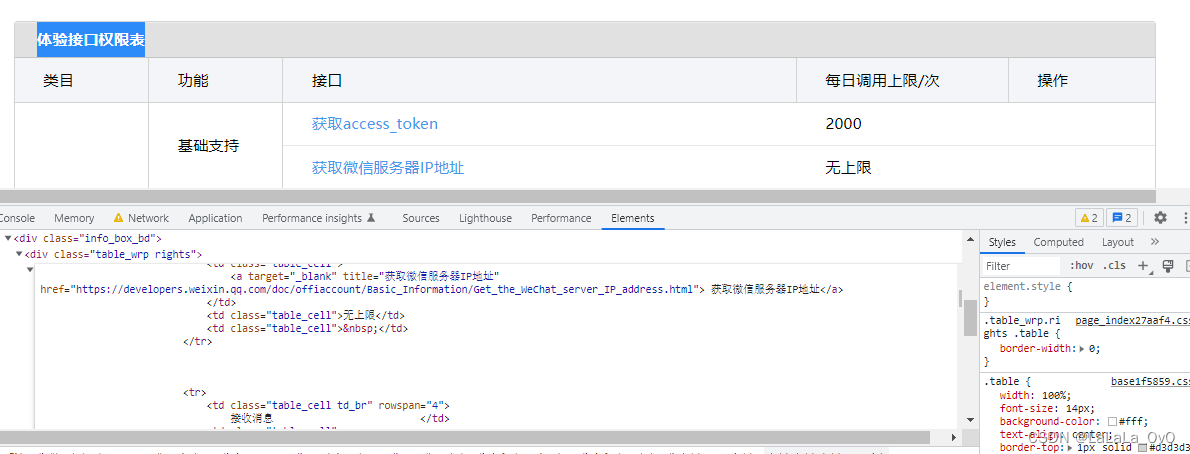
微信公众号开发学习
申请测试号 地址 通过F12抓取体验接口权限表的HTML 解析HTML 引入pom <dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><optional>true</optional></dependency><dependency><…...

【LeetCode】221.最大正方形
题目 在一个由 ‘0 和 ‘1 组成的二维矩阵内,找到只包含 ‘1 的最大正方形,并返回其面积。 示例 1: 输入:matrix [["1","0","1","0","0"],["1","0",&q…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
