动手学深度学习(一)预备知识

目录
一、数据操作
1. N维数组样例
2. 访问元素
3. 基础函数
(1) 创建一个行向量
(2)通过张量的shape属性来访问张量的形状和元素总数
(3)reshape()函数
(4)创建全0、全1、其他常量或从特定分布中随机采样的数字组成的张量
(5)标准运算(张量间的标准运算,都是按元素运算)
(6)拼接函数cat
(7)求和函数sum
(8)矩阵的转置
(9)复制张量
(10)点积,矩阵-向量积和矩阵乘法
(11)范数
4.广播机制
5.转化为Numpy张量
课程推荐:跟李沐学AI的个人空间-跟李沐学AI个人主页-哔哩哔哩视频
一、数据操作
1. N维数组样例
(1)0-d 标量
1.0(2)1-d 向量
[1.0, 2.7, 3.4](3)2-d 矩阵
[[1.0, 2.7, 3.4][5.0, 0.2, 4.6][4.3, 8.5, 0.2]](4)3-d RGB图片(CxHxW)
[[[1.0,2.7,3.4][5.0,0.2,4.6][4.3,8.5,0.2]][[3.2, 5.7, 3.4][5.4, 6.2, 3.2][4.1, 3.5, 6.2]]](5)4-d 一个RGB图片批量(BxCxHxW)
(6)5-d 一个视频批量(TxBxCxHxW)
2. 访问元素
切片规则:[start : end : step]
start : 起始索引,从0开始,-1表示结束。
end:结束索引,不包含。
step:步长,即范围内每次取值的间隔;步长为正时,从左向右取值。步长为负时,反向取值。
(1)访问一个元素
[1, 2]
>>> x = torch.arange(1, 17).reshape(4, 4)
>>> x[1, 2]
tensor(7)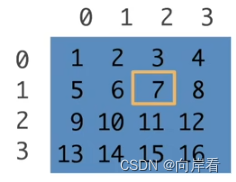
(2)访问一行
[1,:]
>>> x[1,:]
tensor([5, 6, 7, 8])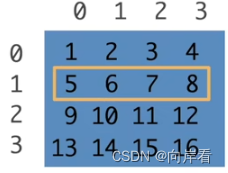
(3)访问一列
[:,1]
>>> x[:,1]
tensor([ 2, 6, 10, 14])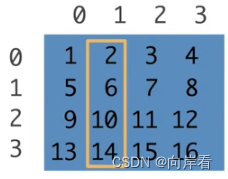
(4)子区域
[1:3,1:]
>>> x[1:3,1:]
tensor([[ 6, 7, 8],[10, 11, 12]])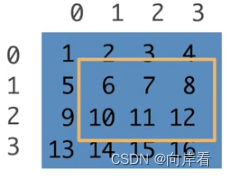
[::3,::2]
>>> x[::3,::2]
tensor([[ 1, 3],[13, 15]])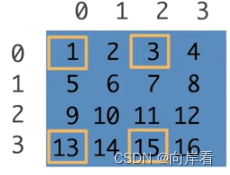
3. 基础函数
(1) 创建一个行向量
x = torch.arange(12)
x #tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])(2)通过张量的shape属性来访问张量的形状和元素总数
x.shape # torch.Size([12])
x.size() # torch.Size([12])(3)reshape()函数
改变一个张量的形状 。
X = x.reshape(3,4)
X
# tensor([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]])(4)创建全0、全1、其他常量或从特定分布中随机采样的数字组成的张量
全0: 第一个参数为张量的shape。
torch.zeros((2,3,4))
# tensor([[[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]],# [[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]]])
全1:
torch.ones((1,3,4))
# tensor([[[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]]])
其他常量(指定值):
torch.tensor([[1,2],[2,1]])
# tensor([[1, 2],
# [2, 1]])(5)标准运算(张量间的标准运算,都是按元素运算)
x = torch.tensor([1.0, 2, 3, 4])
y = torch.tensor([5, 6, 7, 8])
x+y,x-y,x*y,x/y,x**y
# (tensor([ 6., 8., 10., 12.]), tensor([-4., -4., -4., -4.]), tensor([ 5., 12., 21., 32.]), tensor([0.2000, 0.3333, 0.4286, 0.5000]), tensor([1.0000e+00, 6.4000e+01, 2.1870e+03, 6.5536e+04]))
比较运算符,按位比较
x == y
# tensor([False, False, False, False]) * 按位相乘,称为哈达玛乘(数学符号)。
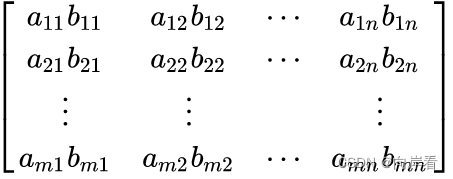
>>> A = torch.arange(9).reshape(3,3)
>>> A
tensor([[0, 1, 2],[3, 4, 5],[6, 7, 8]])
>>> B = torch.arange(9,18).reshape(3,3)
>>> B
tensor([[ 9, 10, 11],[12, 13, 14],[15, 16, 17]])
>>> A * B
tensor([[ 0, 10, 22],[ 36, 52, 70],[ 90, 112, 136]])(6)拼接函数cat
torch.cat(inputs, dim=?)
- inputs : 待连接的张量序列,可以是任意相同
Tensor类型的python 序列- dim : 选择的扩维, 必须在
0到len(inputs[0])之间,沿着此维连接张量序列。
dim=0,表示按第0维方向拼接,即按行方向拼接;dim=1,表示按第0维方向拼接,即按列方向拼接;dim=3……
y = torch.tensor(([[4, 1],[3, 5]]))
x = torch.arange(4, dtype=torch.float32).reshape(2, 2)
torch.cat((x, y), dim=0)
# tensor([[0., 1.],
# [2., 3.],
# [4., 1.],
# [3., 5.]])torch.cat((x, y), dim=1)
# tensor([[0., 1., 4., 1.],
# [2., 3., 3., 5.]])
(7)求和函数sum
参数1,axis:指定求和维度,张量按该维度求和,并将该维度消去。
如,张量形状为[2, 5, 4],axis=0时,求和后,张量形状为[5, 4]。
参数2,keepdims:默认为False,是否保留axis要消去的维度。keepdims=True时,将要消去的维度长度置为1。
如,张量形状为[2, 5, 4],axis=0,keepdims=True时,求和后,张量形状为[1,5, 4]。
1)张量中的所有元素求和:
x = torch.tensor([1.0, 2, 3, 4])
x.sum()
# tensor(10.)2)按行(第0维)求和:
>>> A = torch.arange(9).reshape(3,3)
>>> A
tensor([[0, 1, 2],[3, 4, 5],[6, 7, 8]])>>> A.sum(axis=0)
tensor([ 9, 12, 15])3)按列(第1维)求和:
>>> A.sum(axis=1)
tensor([ 3, 12, 21])2维求和,3维……
4)keepdims(保留维度):
按某一维度求和时,保留该维度,该维度长度置为1。
>>> A
tensor([[0, 1, 2],[3, 4, 5],[6, 7, 8]])>>> A.sum(axis=1).size()
torch.Size([3])>>> A.sum(axis=1,keepdims=True).size()
torch.Size([3, 1])>>> A.sum(axis=1,keepdims=True)
tensor([[ 3],[12],[21]])
# 按列求均值
>>> A/A.sum(axis=1,keepdims=True)
tensor([[0.0000, 0.3333, 0.6667],[0.2500, 0.3333, 0.4167],[0.2857, 0.3333, 0.3810]])5)指定多维度求和
A.sum(axis=[n, m]),按n和m维度求和,求和结果中其他维度不变,将n,m维度消去。
>>> A = torch.arange(8).reshape(2,2,2)
>>> A
tensor([[[0, 1],[2, 3]],[[4, 5],[6, 7]]])# 保留第1维度
>>> A.sum(axis=[0,2]).size()
torch.Size([2])# 使用keepdims保留要消去的维度,将维度长度置为1
>>> A.sum(axis=[0,2],keepdims=True).size()
torch.Size([1, 2, 1])# 输出
>>> A.sum(axis=[0,2])
tensor([10, 18])(8)矩阵的转置
>>> import torch
>>> B = torch.tensor(([1,2,3],[4,5,6],[7,8,9]))
>>> B
tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
>>> B.T
tensor([[1, 4, 7],[2, 5, 8],[3, 6, 9]])(9)复制张量
“=”,复制之后的两个张量共用一个内存地址。
>>> A = B
>>> id(B)
1950198475976
>>> id(A)
1950198475976
>>> B[0]=10
>>> B
tensor([10, 2, 3, 4, 5, 6, 7, 8, 9])
>>> A
tensor([10, 2, 3, 4, 5, 6, 7, 8, 9])clone(),重新分配内存地址。
>>> A=B.clone()
>>> id(A)
1950198519512
>>> id(B)
1950198475976(10)点积,矩阵-向量积和矩阵乘法
向量点积—dot函数(1维):
>>> A = torch.arange(4)
>>> A
tensor([0, 1, 2, 3])
>>> B
tensor([[1., 1., 1.],[1., 1., 1.],[1., 1., 1.]])
>>> B = torch.arange(4, 8)
>>> B
tensor([4, 5, 6, 7])
>>> torch.dot(A, B)
tensor(38)矩阵点积(2维):
按位相乘求和。
>>> A = torch.arange(9).reshape(3,3)
>>> B = torch.arange(9,18).reshape(3,3)>>> torch.sum(A * B)
tensor(528)矩阵-向量积(mv函数):
>>> B = torch.arange(9,18).reshape(3,3)
>>> C = torch.arange(3)>>> torch.mv(B, C)
tensor([32, 41, 50])矩阵乘法(mm函数):
>>> torch.mm(A, B)
tensor([[ 42, 45, 48],[150, 162, 174],[258, 279, 300]])(11)范数
L1范数:
向量元素的绝对值之和。
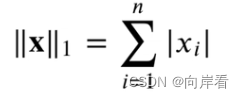
>>> u = torch.tensor([3.0, -4.0])
>>> torch.abs(u).sum()
tensor(7.)L2范数:
向量元素平方和的平方根。

>>> u = torch.tensor([3.0, -4.0])
>>> torch.norm(u)
tensor(5.)弗罗贝尼乌斯-范数(F-范数):
矩阵元素的平方和的平方根。
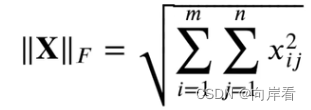
>>> torch.norm(torch.ones(4, 9))
tensor(6.)4.广播机制
1.通过适当复制元素来扩展一个或两个数组,以便在转换之后,两个张量具有相同的形状。
2.对于生成的数组执行按元素操作。
y = torch.arange(12).reshape(3,2,2)
y
# tensor([[[ 0, 1],
# [ 2, 3]],
#
# [[ 4, 5],
# [ 6, 7]],# [[ 8, 9],
# [10, 11]]])x = torch.tensor([[1,2],[3,4]])
x# tensor([[1, 2],
# [3, 4]])x + y# tensor([[[ 1, 3],
# [ 3, 5]],# [[ 5, 7],
# [ 7, 9]],# [[ 9, 11],
# [11, 13]]])5.转化为Numpy张量
A = x.numpy()
type(A)
# <class 'numpy.ndarray'>相关文章:
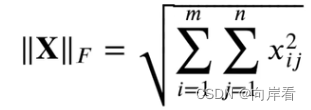
动手学深度学习(一)预备知识
目录 一、数据操作 1. N维数组样例 2. 访问元素 3. 基础函数 (1) 创建一个行向量 (2)通过张量的shape属性来访问张量的形状和元素总数 (3)reshape()函数 (4)创建全0、全1、…...
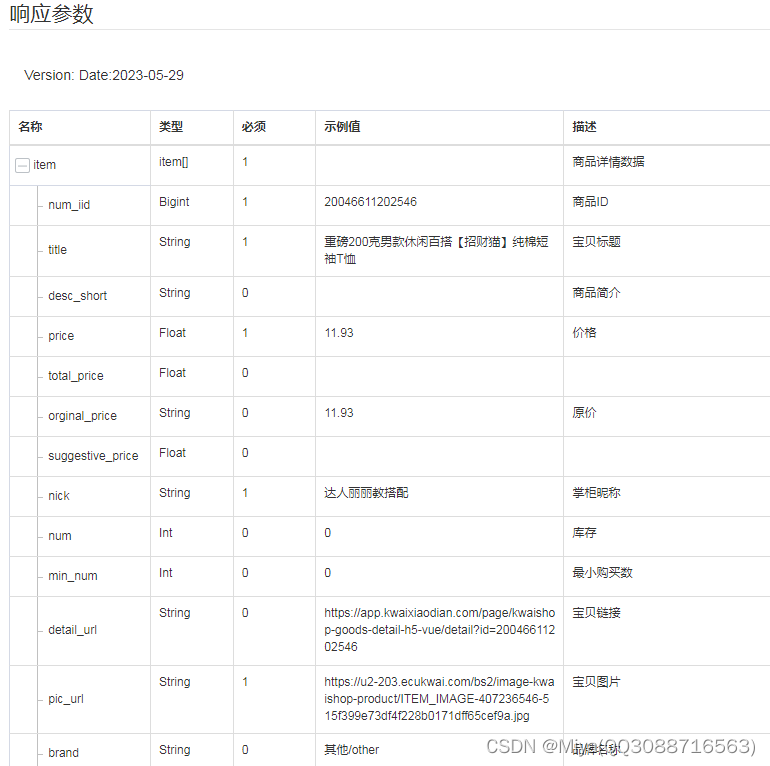
item_get-KS-获取商品详情
一、接口参数说明: item_get-根据ID取商品详情 ,点击更多API调试,请移步注册API账号点击获取测试key和secret 公共参数 请求地址: https://api-gw.onebound.cn/ks/item_get 名称类型必须描述keyString是调用key(http://o0b.cn/…...
)
[华为OD] 最小传输时延(dijkstra算法)
明天就要面试了我也太紧张了吧 但是终于找到了一个比较好理解的dijkstra的python解法,让我快点把它背下来!!!! 文章目录 题目dijkstra算法的python实现python解答dfs解法dijkstra解法 题目 先把题目放出来 某通信网络…...

问道管理:总资产大于总市值好吗?
在财政领域,总财物和总市值是两个非常重要的指标。总财物是指公司所有的财物,包括固定财物、流动财物、无形财物等,而总市值则是指公司股票在商场上的总价值。当总财物大于总市值时,这是否是一个好的信号呢?咱们将从多…...
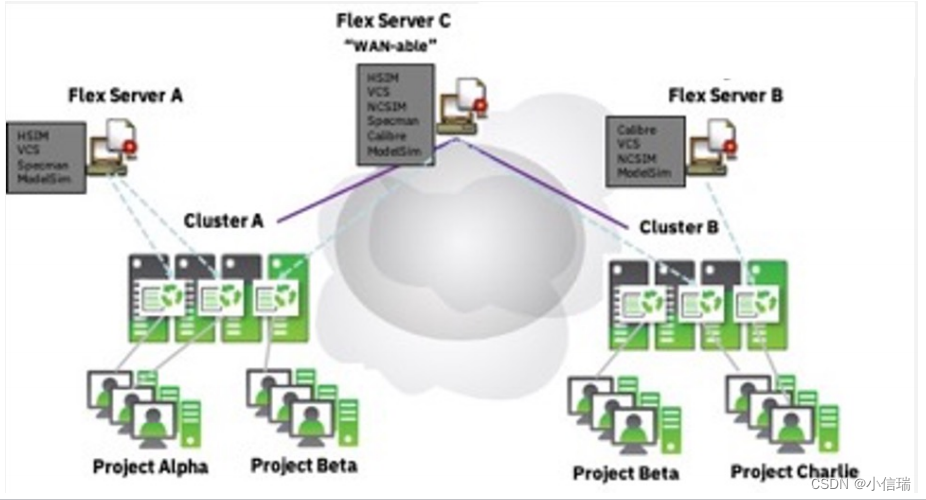
IBM Spectrum LSF (“LSF“ ,简称为负载共享设施) 用户案例
IBM Spectrum LSF (“LSF” ,简称为负载共享设施) 用户案例 IBM Spectrum LSF (“LSF” ,简称为负载共享设施) 软件是业界领先的企业级软件。 LSF 在现有异构 IT 资源之间分配工作,以创建共享,可扩展且容错的基础架构,…...
Pytorch深度学习-----神经网络之非线性激活的使用(ReLu、Sigmoid)
系列文章目录 PyTorch深度学习——Anaconda和PyTorch安装 Pytorch深度学习-----数据模块Dataset类 Pytorch深度学习------TensorBoard的使用 Pytorch深度学习------Torchvision中Transforms的使用(ToTensor,Normalize,Resize ,Co…...
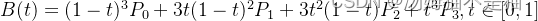
Gis入门,使用起止点和两个控制点生成三阶贝塞尔曲线(共四个控制点,线段转曲线)
前言 本章讲解如何在gis地图中使用起止点和两个控制点(总共四个控制点)生成三阶贝塞尔曲线。 二阶贝塞尔曲线请参考上一章《Gis入门,如何根据起止点和一个控制点计算二阶贝塞尔曲线(共三个控制点)》 贝塞尔曲线(Bezier curve)介绍 贝塞尔曲线(Bezier curve)是一种…...
Web-7-深入理解Cookie与Session:实现用户跟踪和数据存储
深入理解Cookie与Session:实现用户跟踪和数据存储 今日目标 1.掌握客户端会话跟踪技术Cookie 2.掌握服务端会话跟踪技术Sesssion 1.会话跟踪技术介绍 会话:用户打开浏览器,访问web服务器的资源,会话建立,直到有一方断…...

Springboot设置Https
1、修改配置文件application.yml,并将*.jks放到resource目录下。 server:port: 8080ssl:key-store: classpath:*.jkskey-store-password: *key-store-type: JKSenabled: truekey-alias: boe.com.cn2、添加http转https的配置 Configuration public class TomcatCon…...
Windows 使用 Linux 子系统,轻轻松松安装多个linux
Windows Subsystem for Linux WSL 简称WSL,是一个在Windows 10\11上能够运行原生Linux二进制可执行文件(ELF格式)的兼容层。它是由微软与Canonical公司合作开发,其目标是使纯正的Ubuntu、Debian等映像能下载和解压到用户的本地计算机&#…...
中级课程——弱口令(认证崩溃)
文章目录 什么是弱口令密码生成器分类暴力破解万能密码测试环境工具 什么是弱口令 密码生成器 分类 暴力破解 万能密码 or true --测试环境 工具 九头蛇,超级弱口令爆破工具,bp,...

web自动化测试进阶篇05 ——— 界面交互场景测试
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:【Austin_zhai】 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能,分享行业相关最新信息。…...

NICE-SLAM: Neural Implicit Scalable Encoding for SLAM论文阅读
论文信息 标题:NICE-SLAM: Neural Implicit Scalable Encoding for SLAM 作者:Zihan Zhu, Songyou Peng,Viktor Larsson — Zhejiang University 来源:CVPR 代码:https://pengsongyou.github.io/nice-slam…...
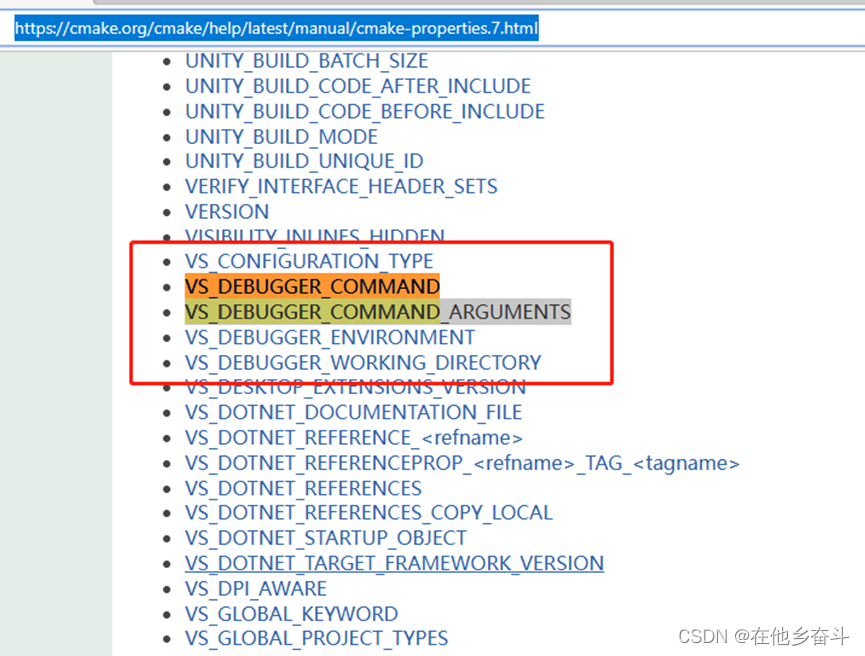
cmake 配置Visual studio的调试命令
配置代码如截图: set_property(TARGET ${TARGET_NAME} PROPERTY VS_DEBUGGER_COMMAND "./consoleTest.exe") set_property(TARGET ${TARGET_NAME} PROPERTY VS_DEBUGGER_COMMAND_ARGUMENTS "./config/labelDriver.cfg") set_propert…...
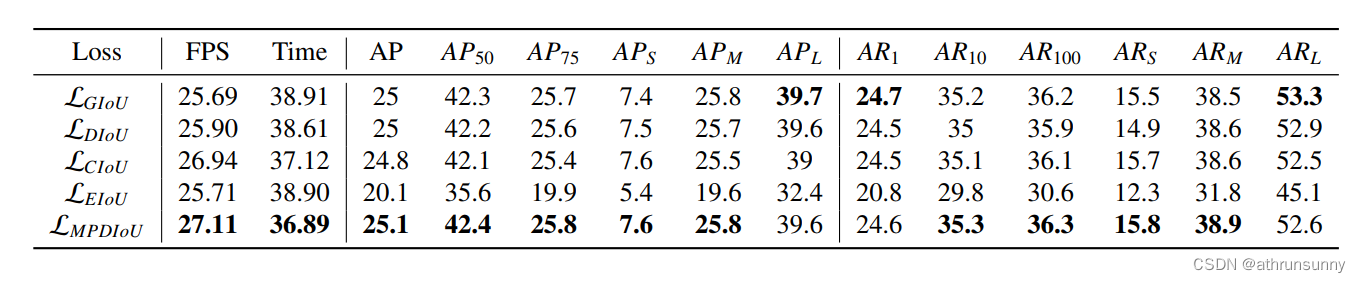
MPDIoU: A Loss for Efficient and Accurate Bounding BoxRegression--论文学习笔记
超越GIoU/DIoU/CIoU/EIoU MPDIoU让YOLOv7和YOLACT双双涨点 目标检测上的指标对比: 论文地址: [2307.07662] MPDIoU: A Loss for Efficient and Accurate Bounding Box Regression (arxiv.org) 摘要 边界框回归(Bounding Box Regression&am…...
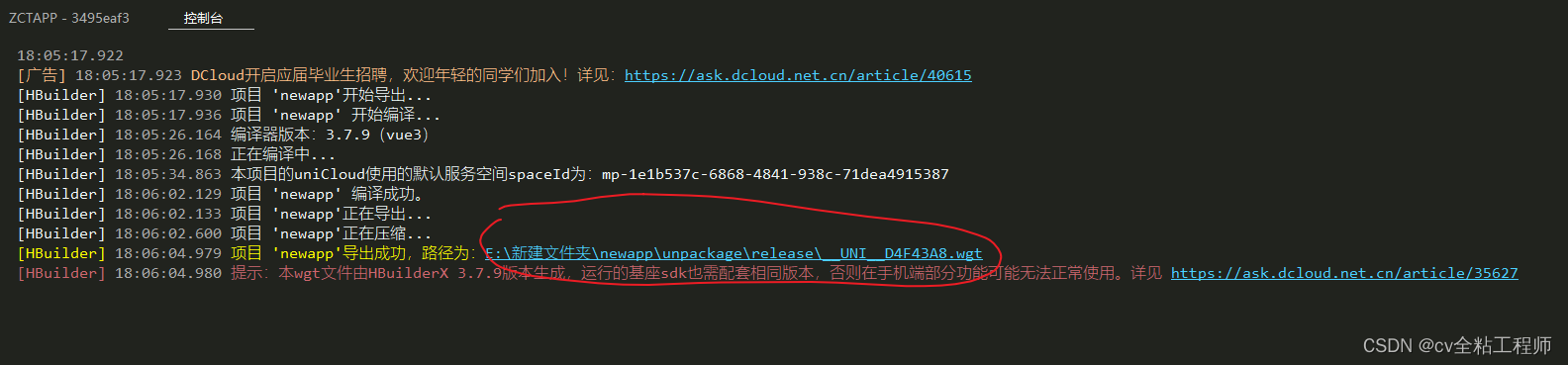
【Uniapp 的APP热更新】
Uniapp 的APP热更新功能依赖于其打包工具 HBuilder,具体步骤如下: 1. 在 HBuilder 中构建并打包出应用程序 具体步骤: 1.点击发行,点击制作wgt包 2.根据需求修改文件储存路径和其他配置,点击确定 3.等待打包完成&a…...

MySQL主从复制配置
Mysql的主从复制至少是需要两个Mysql的服务,当然Mysql的服务是可以分布在不同的服务器上,也可以在一台服务器上启动多个服务。 (1)首先确保主从服务器上的Mysql版本相同 (2)在主服务器上,创建一个充许从数据库来访问的用户slave,密码为:123456 ,然后使用REPLICATION SLAV…...

Linux - 添加普通用户为信任用户
1.添加用户 在Linux系统中,可以使用以下步骤添加用户: 打开终端并以root用户身份登录 输入以下命令以创建新用户(请将username替换为您想要创建的用户名): adduser username 设置该用户的密码,使用以下命…...

flask----路由系统
# 1 flask路由系统是基于装饰器的:参数如下 # 2 转换器: # 3 路由系统本质 # 4 endpoint 不传会怎么样,不传会以视图函数的名字作为值,但是如果加了装饰器,所有视图函数名字都是inner,就会出错,使用wrapp…...

驶向专业:嵌入式开发在自动驾驶中的学习之道
导语: 自动驾驶技术在汽车行业中的快速发展为嵌入式开发领域带来了巨大的机遇。作为自动驾驶的核心组成部分,嵌入式开发在驱动汽车的智能化和自主性方面发挥着至关重要的作用。本文将探讨嵌入式开发的学习方向、途径以及未来在自动驾驶领域中的展望。 一、学习方向:…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
