当前位置： 首页 > news >正文

go程序使用tcp短连接报：only one usage of each socket address

news 2026/2/11 6:10:19

环境及现象

  • Win10
  • 上位机（C#,WPF）
  • 后台使用go作为服务。

连接情况

C#连接大概60个TCP长连接（设备）。
后台go服务连接60个UDP短连接（设备附属硬件），
10个TCP短连接（PLC,modbus通讯），
经常每隔两三天，电脑就什么都连接不上，手动使用modbus 助手调试，报如下错误，需要重启才能解决。
如下图所示：
在这里插入图片描述

解决方法：

参考文章：https://blog.csdn.net/MBuger/article/details/83088894
在这里插入图片描述
待观察是否还会出现连接不上的情况。

相关文章：

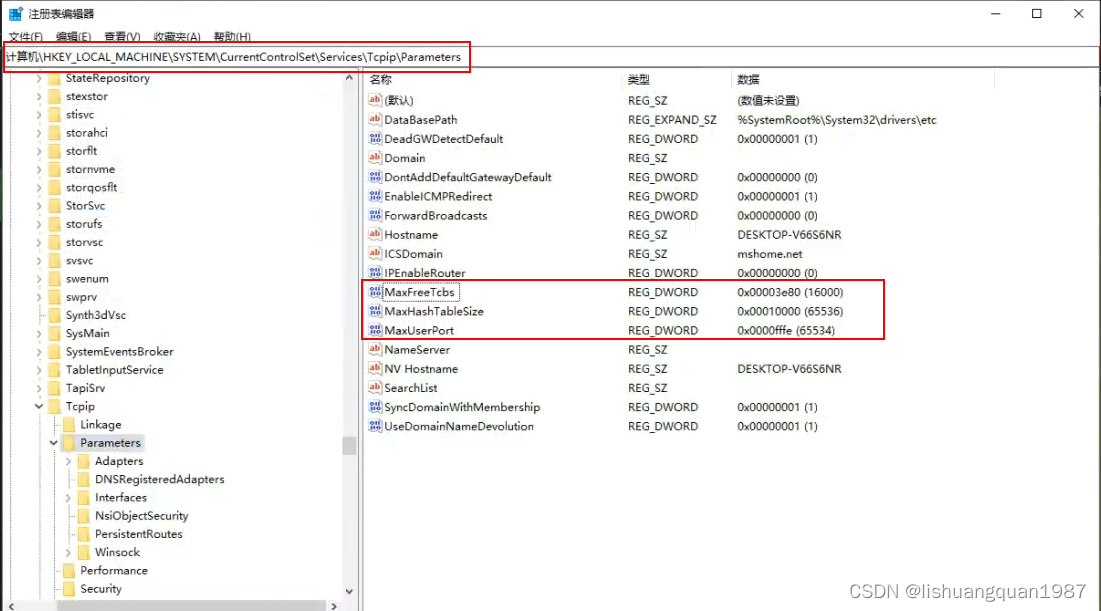
go程序使用tcp短连接报：only one usage of each socket address

环境及现象 Win10上位机（C#,WPF）后台使用go作为服务。 连接情况 C#连接大概60个TCP长连接（设备）。 后台go服务连接60个UDP短连接（设备附属硬件）， 10个TCP短连接（PLC,modbus通讯&a…...

编程日记 2023/8/2 12:31:11

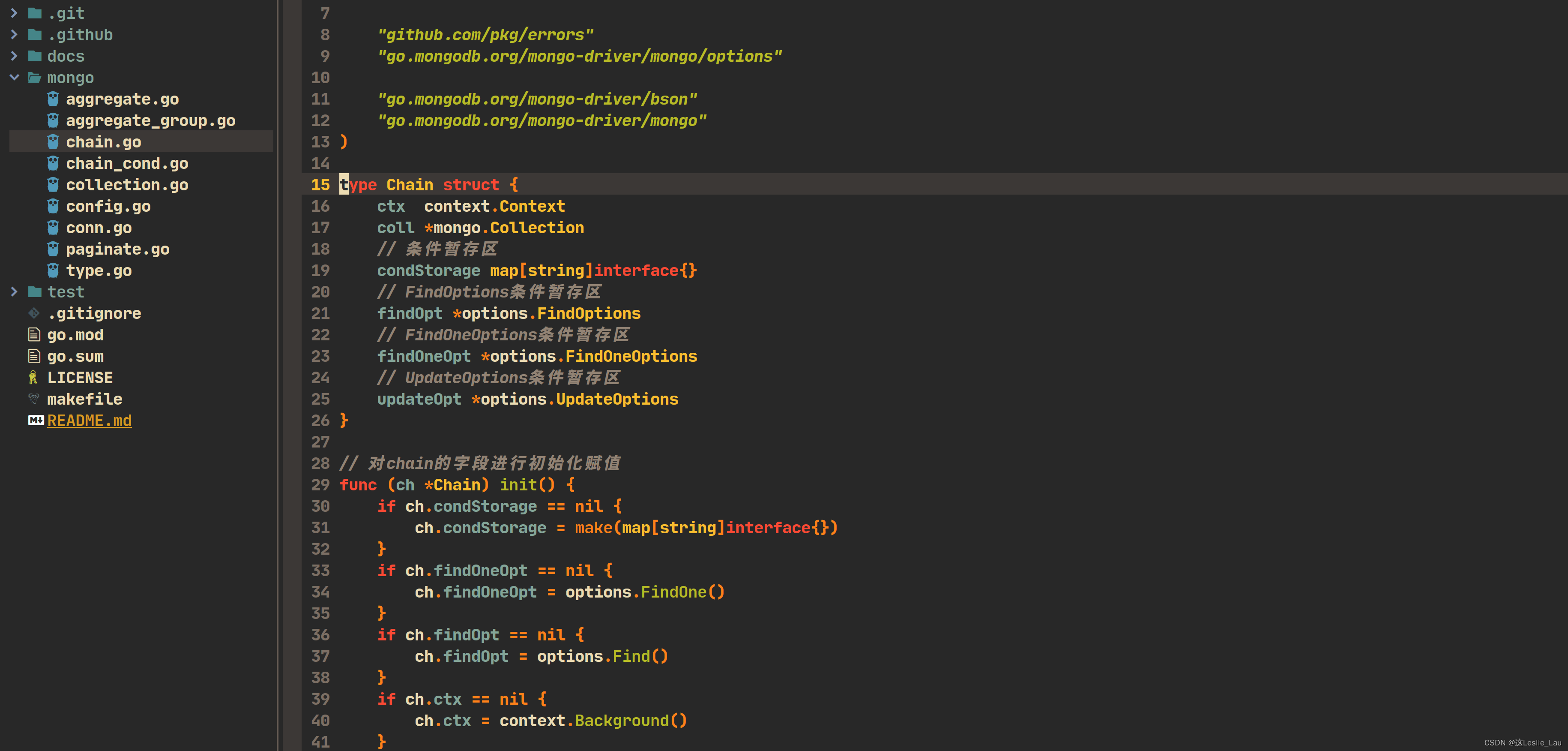
十分钟配置好Neovim go开发环境（其他语言一样）

文章目录 前言仓库地址用法快捷键问题反馈 前言 这篇文章的目的是为了分享下我自己的Neovim配置。 本人是Golang程序员，最开始使用的IDE是JetBrains Goland。有一说一这个ide适配度很高，认识的很多人都使用这个。但是它也有几个对我来说的缺点&#xf…...

编程日记 2023/8/2 12:29:10

Linux第八章之进程概念

一、冯诺依曼体系结构 关于冯诺依曼，必须强调几点： 这里的存储器指的是内存不考虑缓存情况，这里的CPU能且只能对内存进行读写，不能访问外设(输入或输出设备)外设(输入或输出设备)要输入或者输出数据，也只能写入内存或…...

编程日记 2023/8/2 12:28:09

怎么学习Java并发编程相关技术？ - 易智编译EaseEditing

学习Java并发编程可以通过多种方式进行，包括但不限于以下几种： 在线教程和学习平台： 网上有许多免费和付费的Java并发编程教程和学习平台，如Coursera、Udemy、edX、Codecademy等。这些平台提供结构化的课程和练习，适…...

编程日记 2023/8/2 12:27:07

vue3 +element动态表单实现

可以直接复制&#xff0c;接口看后端 父页面 <schedulesref"schedulesRef":dxbz"props.dxbz":jdlx"props.jdlx":woId"myWoId":addendumList"formInline.addendumList"v-if"addendumShow"addendum"addendu…...

编程日记 2023/8/2 12:26:05

Linux部署jar包，隐藏命令行参数

Linux部署jar包&#xff0c;隐藏命令行参数 一、背景需求二、查阅资料三、实现隐藏库3.1、测试test.c3.2、设置隐藏库3.3、验证 四、应用jar启动命令五、直接应用结果 最新项目安全检测&#xff0c;发现配置文件中数据库密码&#xff0c;redis密码仍处理明文状态 于是整理了一篇…...

编程日记 2023/8/2 12:25:04

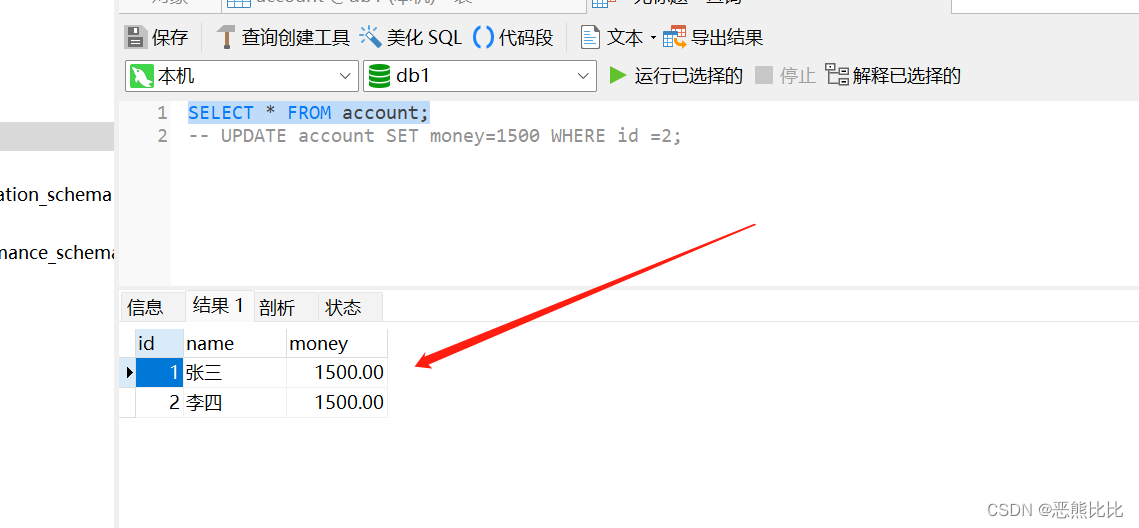
JDBC-笔记

JDBC 1. JDBC介绍 JDBC&#xff08;Java Database Connectivity&#xff09;是一种用于连接和操作数据库的 Java API。 通过Java操作数据库的流程 第一步&#xff1a;编写Java代码 第二步&#xff1a;Java代码将SQL发送到MySQL服务端 第三步&#xff1a;MySQL服务端接收到SQ…...

编程日记 2023/8/2 12:24:03

Rust的入门篇(中)

Rust的入门篇(中) 这是接上面一篇rust入门篇(上)文章 22. 包管理一 mod nation {pub mod government {pub fn govern() {}}mod congress {pub fn legislate() {}}mod court {fn judicial() {super::congress::legislate();}} }fn main() {nation::government::govern(); }23.…...

编程日记 2023/8/2 12:23:02

手机设置全局代理ip步骤

在互联网时代&#xff0c;隐私和安全问题备受关注。使用全局代理能够帮助我们保护个人信息&#xff0c;突破地理限制&#xff0c;并提高网络速度。但是&#xff0c;你是否对全局代理的安全性存有疑虑&#xff1f;而且&#xff0c;如何在手机上设置全局代理呢&#xff1f;今天就…...

编程日记 2023/8/2 12:21:59

spring boot+thymeleaf+semantic ui 分页

参考&#xff1a; https://my.oschina.net/ayyao/blog/898041 后端 springboot 使用&#xff1a; com.github.pagehelper.PageInfo&#xff0c;作为分页对象 <!--引入分页插件--> <dependency><groupId>com.github.pagehelper</groupId><artifa…...

编程日记 2023/8/2 12:20:57

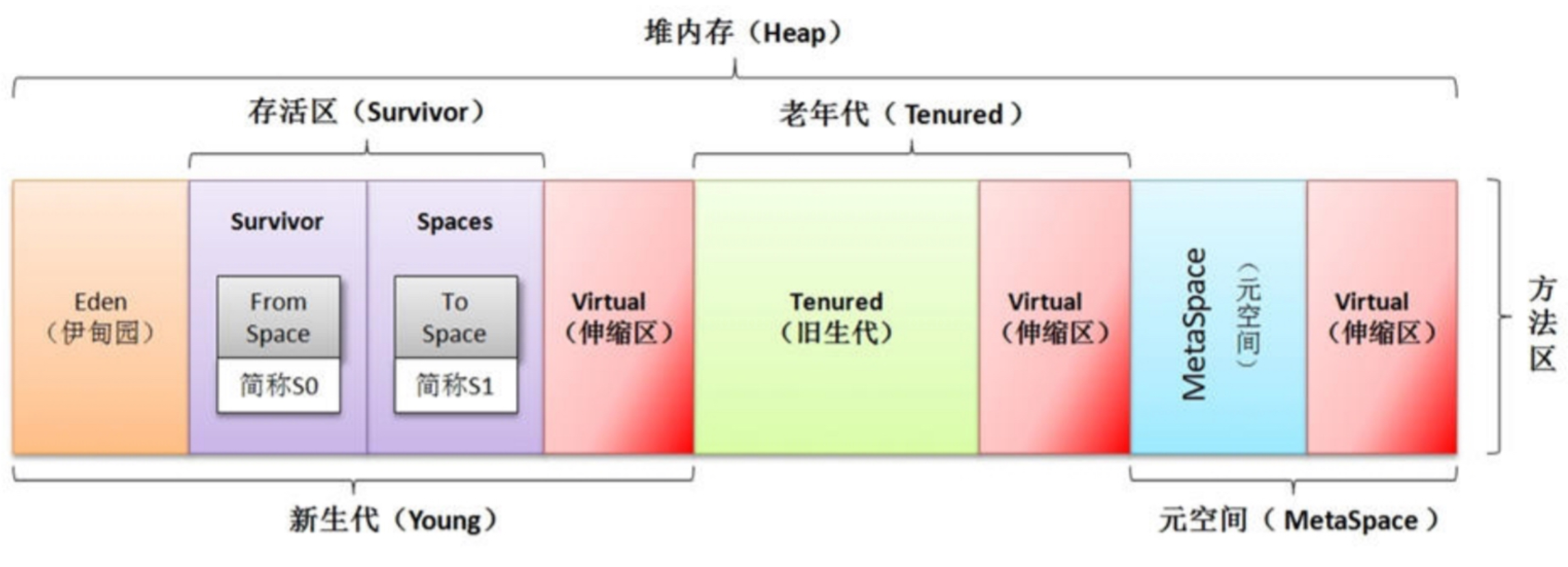
【JVM】（一）深入理解JVM运行时数据区

文章目录 一、JVM 运行流程二、虚拟机栈&#xff08;线程私有&#xff09;三、本地方法栈 &#xff08;线程私有&#xff09;四、方法区&#xff08;元数据区&#xff09;五、堆&#xff08;线程共享&#xff09;六、程序计数器&#xff08;线程私有&#xff09; 一、JVM 运行流…...

编程日记 2023/8/2 12:19:57

C++ QRegExpValidator

//正在表达式限制输入 QString str "\\b(?:(?:25[0-5]|2[0-4][0-9]|[01]?[0-9][0-9]?)\\.){3}(?:25[0-5]|2[0-4][0-9]|[01]?[0-9][0-9]?)\\b"; ui->lineEdit->setValidator(new QRegExpValidator(QRegExp(str))); //用于占位 ui->lineEdit->setI…...

编程日记 2023/8/2 12:18:55

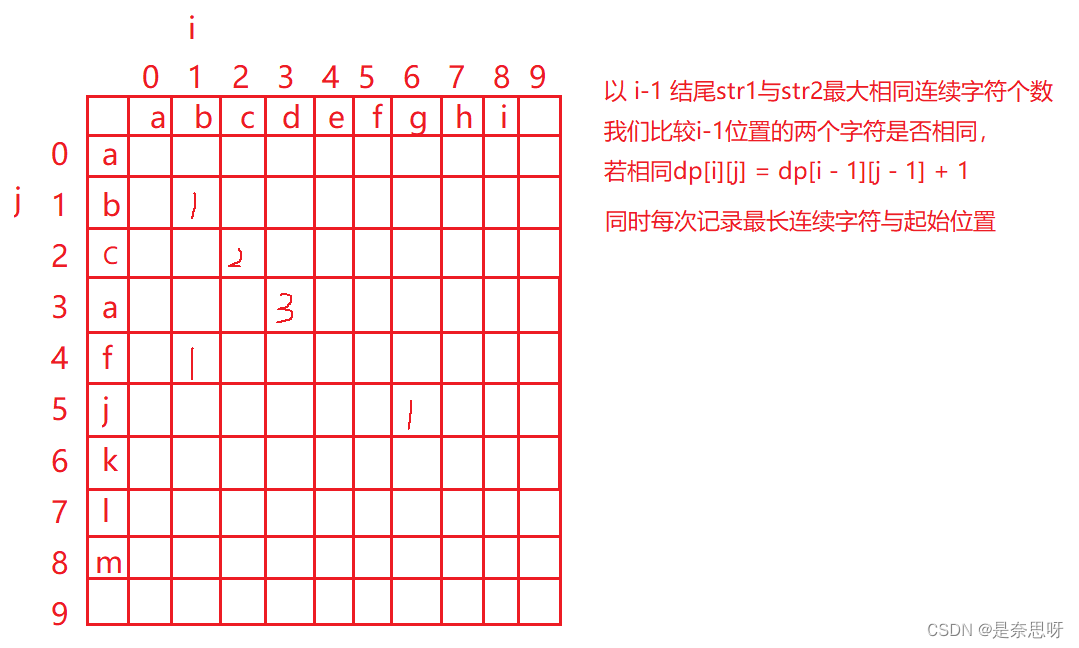
备战秋招 | 笔试强训19

目录 一、选择题 二、编程题 三、选择题题解 四、编程题题解 一、选择题 1、二分查找的时间复杂度&#xff08;&#xff09; A. O(N*log(N)) B. O(N) C. O(log(N)) D. O(N^2) 2、有一个单向链表中有一个A、B两个相邻元素&#xff0c;有一个指针p指向元素A&#xff0c;现将…...

编程日记 2023/8/2 12:17:54

第一章 计算机网络概述

第一章 计算机网络概述 1.1 计算机网络在信息时代的作用 1.2 因特网概述 网络分类&#xff1a; 网络&#xff1a;许多计算机连接在一起的的局域网&#xff1b; 互联网&#xff1a;internet许多网络连接在一起&#xff1b; 因特网&#xff1a;Internet 全球最大的互联网&…...

编程日记 2023/8/2 12:16:53

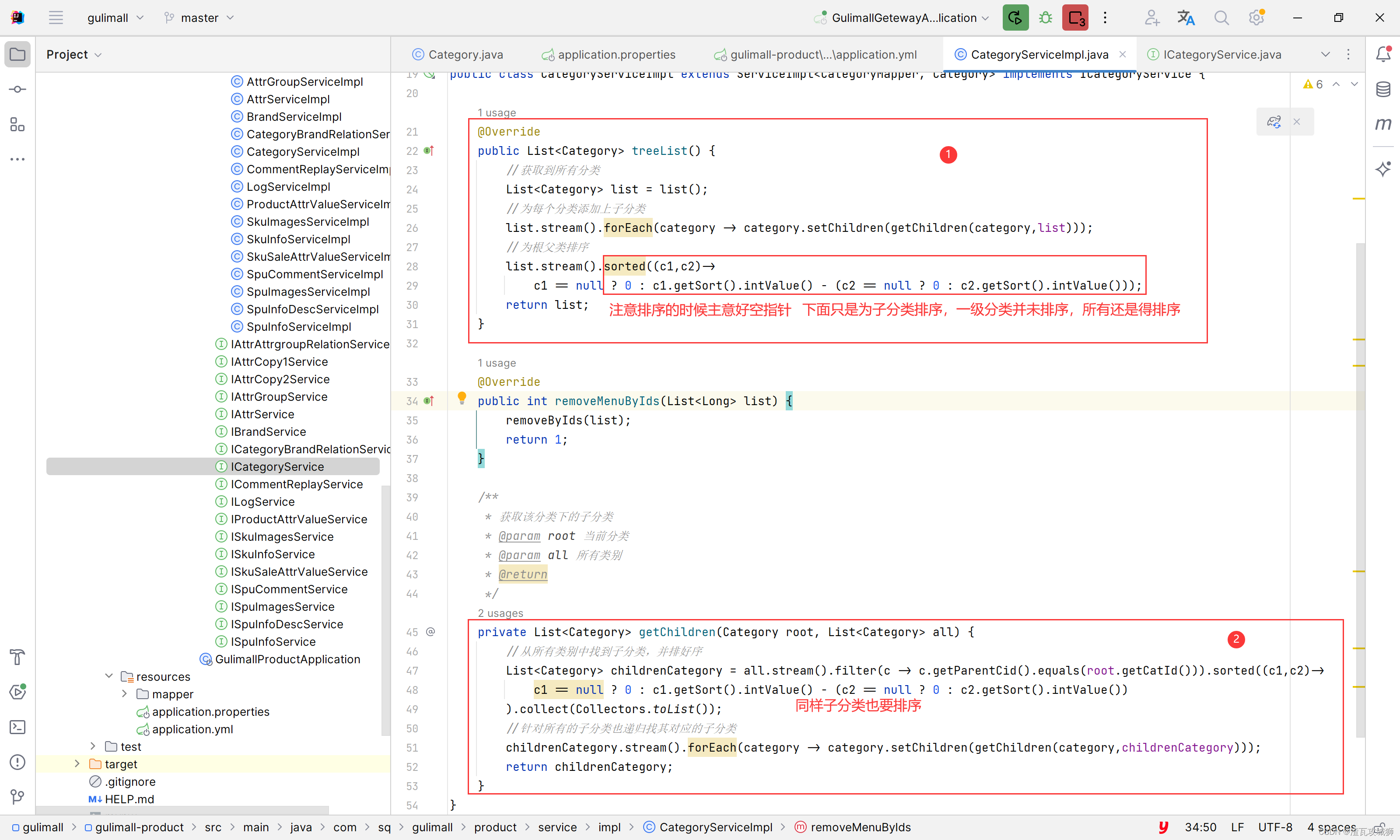
谷粒商城第六天-商品服务之分类管理下的获取三级分类树形列表

目录 一、总述 1.1 前端思路 1.2 后端思路 二、前端部分 2.1 在网页中建好目录及菜单 2.1.1 建好商品目录 2.1.2 建好分类管理菜单 ​编辑 2.2 编写组件 2.2.1 先完成组件文件的创建 2.2.2 编写组件 2.2.2.1 显示三级分类树形列表 三、后端部分 3.1 编写商品分类…...

编程日记 2023/8/2 12:15:52

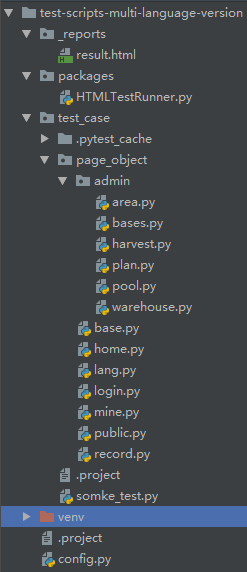
【UI自动化测试】Appium+Python+Unittest+HTMLRunner

简介 获取AppPackage和AppActivity 定位UI控件的工具 脚本结构 PageObject分层管理 HTMLTestRunner生成测试报告 启动appium server服务 以python文件模式执行脚本生成测试报告 【B站最通俗易懂】Python接口自动化测试从入门到精通&#xff0c;超详细的进阶教程&#xff0c;看完…...

编程日记 2023/8/2 12:14:50

【限时优惠】红帽openstack管理课程(CL210) 即将开课

课程介绍 通过实验室操作练习&#xff0c;学员将能够深入学习红帽企业 Linux OpenStack 平台各服务的手动安装方法&#xff0c;还将了解 OpenStack 开发社区的未来发展计划。 培训地点&#xff1a; 线下面授&#xff1a;苏州市姑苏区干将东路666号401室&#xff1b; 远程…...

编程日记 2023/8/2 12:13:49

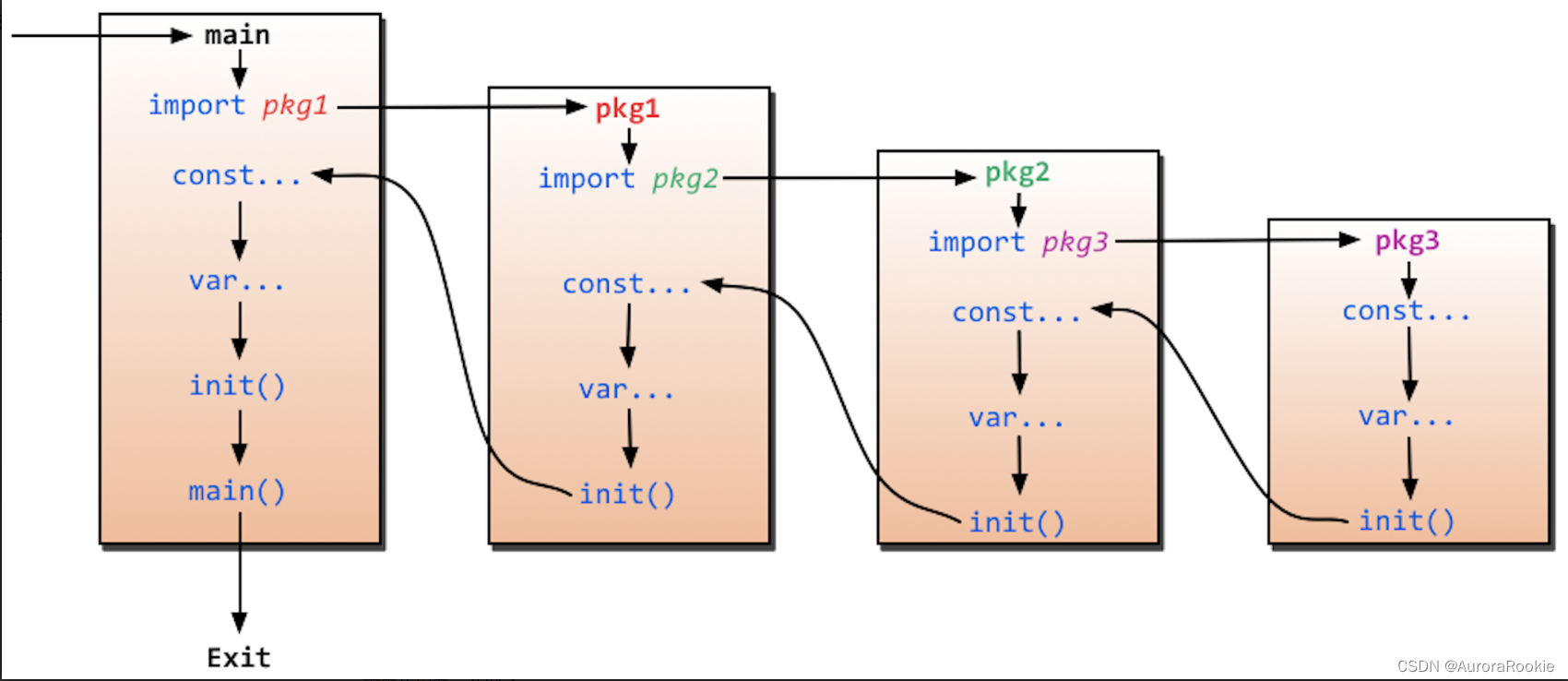
Golang之路---02 基础语法——函数

函数 函数定义 func function_name( [parameter list] ) [return_types] {函数体 }参数解释&#xff1a; func&#xff1a;函数由 func 开始声明function_name&#xff1a;函数名称&#xff0c;函数名和参数列表一起构成了函数签名。[parameter list]&#xff1a;参数列表&a…...

编程日记 2023/8/2 12:12:47

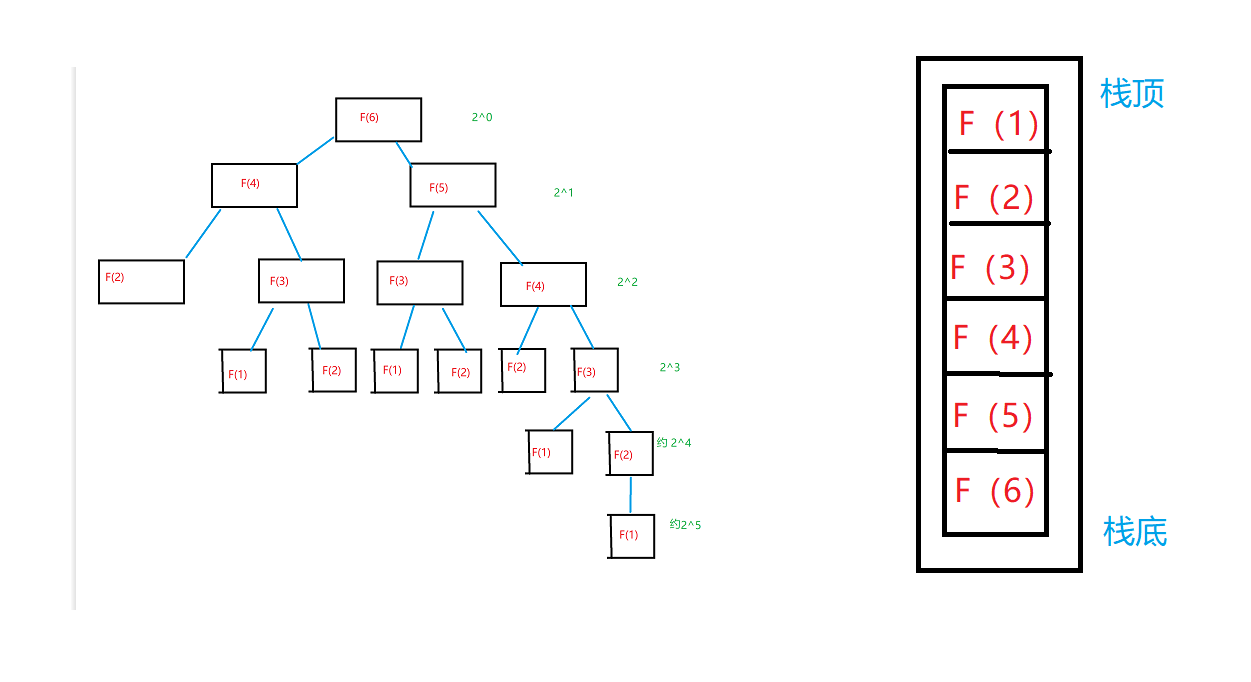
数据结构和算法入门（时间/空间复杂度介绍--java版）

数据结构和算法入门&#xff08;时间/空间复杂度介绍–java版&#xff09; write in front 作者&#xff1a; 向大佬学习 专栏&#xff1a; 数据结构&#xff08;java版&#xff09; 作者简介&#xff1a;大二学生 希望能学习其同学和大佬的经验&#xff01; 本篇博客简介&…...

编程日记 2023/8/2 12:11:46

Spring Mvc 文件上传（MultipartFile ）—官方原版

一、创建应用程序类 要启动Spring Boot MVC应用程序&#xff0c;首先需要一个启动器。在这个示例中&#xff0c;已经添加了spring-boot-starter thymelaf和spring-boot-starter web作为依赖项。要使用Servlet容器上传文件&#xff0c;您需要注册一个MultipartConfigElement类&…...

编程日记 2023/8/2 12:10:45

Cursor实现用excel数据填充word模版的方法

cursor主页&#xff1a;https://www.cursor.com/ 任务目标&#xff1a;把excel格式的数据里的单元格&#xff0c;按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例&#xff0c;…...

编程新知 2025/8/23 5:46:26

51c自动驾驶~合集58

我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留&#xff0c;CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制&#xff08;CCA-Attention&#xff09;&#xff0c;…...

编程新知 2026/2/5 4:25:15

三维GIS开发cesium智慧地铁教程（5）Cesium相机控制

一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点&#xff1a; 路径验证&#xff1a;确保相对路径.…...

编程新知 2025/12/1 19:23:04

可靠性+灵活性：电力载波技术在楼宇自控中的核心价值

可靠性灵活性&#xff1a;电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中&#xff0c;电力载波技术&#xff08;PLC&#xff09;凭借其独特的优势&#xff0c;正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据&#xff0c;无需额外布…...

编程新知 2025/9/27 2:43:26

蓝牙 BLE 扫描面试题大全(2)：进阶面试题与实战演练

前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1)&#xff1a;从基础到实战的深度解析-CSDN博客&#xff0c;但实际面试中&#xff0c;企业更关注候选人对复杂场景的应对能力&#xff08;如多设备并发扫描、低功耗与高发现率的平衡&#xff09;和前沿技术的…...

编程新知 2026/2/5 3:41:42

基于当前项目通过npm包形式暴露公共组件

1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹&#xff0c;并新增内容 3.创建package文件夹...

编程新知 2026/2/1 21:58:45

五年级数学知识边界总结思考-下册

目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解&#xff1a;由来、作用与意义**一、知识点核心内容****二、知识点的由来&#xff1a;从生活实践到数学抽象****三、知识的作用&#xff1a;解决实际问题的工具****四、学习的意义&#xff1a;培养核心素养…...

编程新知 2025/10/7 4:57:55

ElasticSearch搜索引擎之倒排索引及其底层算法

文章目录 一、搜索引擎1、什么是搜索引擎？2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长，文件大。2.其次，树深，IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

编程新知 2026/1/30 17:10:19

关于 WASM：1. WASM 基础原理

一、WASM 简介 1.1 WebAssembly 是什么&#xff1f; WebAssembly&#xff08;WASM&#xff09; 是一种能在现代浏览器中高效运行的二进制指令格式&#xff0c;它不是传统的编程语言&#xff0c;而是一种 低级字节码格式&#xff0c;可由高级语言&#xff08;如 C、C、Rust&am…...

编程新知 2025/11/19 10:53:07

【Oracle】分区表

个人主页&#xff1a;Guiat 归属专栏&#xff1a;Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

编程新知 2026/1/20 21:59:36