备战秋招 | 笔试强训19
目录
一、选择题
二、编程题
三、选择题题解
四、编程题题解
一、选择题
1、二分查找的时间复杂度()
A. O(N*log(N))
B. O(N)
C. O(log(N))
D. O(N^2)
2、有一个单向链表中有一个A、B两个相邻元素,有一个指针p指向元素A,现将一个指针r指向的S元素要插入到A和B之间,该进行操作()
A. p->next=p->next->next
B. r-next=p;p->next=r->next
C. r->next=p->next;p->next=r
D. r=p->next;->next=r->next
E. r->next=p;p->next=r
F. p=p->next->next
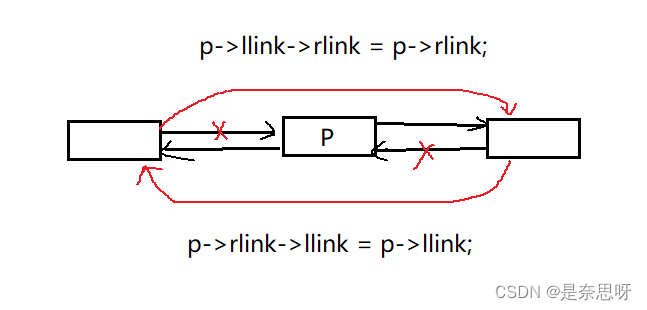
3、双向链表中有两个指针域,llink和rlink分别指向前驱和后继,设p指向链表中的一个结点,现要求删去p所指结点,则正确的删除是()(链中结点数大于2,p不是第一个结点)
A. p->llink->rlink:=p->llink; p->llink->rlink:=p->rlink; dispose(p);
B. dispose(p); p->llink->rlink:=p->llink; p->llink->rlink:=p->rlink;
C. p->link->rlink:=p->llink; dispose(p); p->llink->rlink:=p->rlink;
D. 以上A,B,C都不对
4、一个栈的入栈序列是A,B,C,D,E,则栈的不可能输出序列是()
A. EDCBA
B. DECBA
C. DCEAB
D. ABCDE
5、循环队列放在一维数组A[0…M-1]中,end1指向队头元素,end2指向队尾元素的后一个位置。假设队列两端均可进行入队和出队操作,队列中最多能容纳M-1个元素。初 始时为空,下列判断队空和队满的条件中,正确的是()
A. 队空:end1==end2;队满:end1==(end2+1) mod M
B. 队空:end1==end2;队满:end2==(end1+1) mod (M-1)
C. 队空:end2==(end1+1) mod M;队满:end1==(end2+1) mod M
D. 队空:end1==(end2+1) mod M;队满:end2==(end1+1) mod (M-1)
6、已知二叉树后序遍历序列是bfegcda,中序遍历序列是badefcg,它的前序遍历序列是()
A. abcdefg
B. abdcefg
C. adbcfeg
D. abecdfg
7、某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为()
A. 不存在这样的二叉树
B. 200
C. 198
D. 199
8、设有一组记录的关键字为{19,14,23,1,68,20,84,27,55,11,10,79},用链地址法构造哈希表,哈希函数为H(key)=key MOD 13,哈希地址为1的链中有()个记录
A. 1
B. 2
C. 3
D. 4
9、以下哪种排序是不稳定排序()
A. 冒泡
B. 插入排序
C. 归并排序
D. 快速排序
二、编程题
1、汽水瓶 题目链接
 2、查找两个字符串a,b中的最长公共子串 题目链接
2、查找两个字符串a,b中的最长公共子串 题目链接

三、选择题题解
1、二分查找的时间复杂度()
A. O(N*log(N))
B. O(N)
C. O(log(N))
D. O(N^2)
正确答案:C
题解:
基本概念题;
2、有一个单向链表中有一个A、B两个相邻元素,有一个指针p指向元素A,现将一个指针r指向的S元素要插入到A和B之间,该进行操作()
A. p->next=p->next->next
B. r-next=p;p->next=r->next
C. r->next=p->next;p->next=r
D. r=p->next;->next=r->next
E. r->next=p;p->next=r
F. p=p->next->next
正确答案: C
题解:
如下图所示,我们要插入一个新的结点;
3、双向链表中有两个指针域,llink和rlink分别指向前驱和后继,设p指向链表中的一个结点,现要求删去p所指结点,则正确的删除是()(链中结点数大于2,p不是第一个结点)
A. p->llink->rlink:=p->llink; p->llink->rlink:=p->rlink; dispose(p);
B. dispose(p); p->llink->rlink:=p->llink; p->llink->rlink:=p->rlink;
C. p->link->rlink:=p->llink; dispose(p); p->llink->rlink:=p->rlink;
D. 以上A,B,C都不对
正确答案;D
题解:
正确代码我们可以结合下图来看;
4、一个栈的入栈序列是A,B,C,D,E,则栈的不可能输出序列是()
A. EDCBA
B. DECBA
C. DCEAB
D. ABCDE
正确答案:C
题解:
C选项,当我们第一个出D时,代表ABC已经入栈,此时我们出一个C,栈中还有AB,我们再入一个E,然后再出一个E,接着栈顶的元素应该是B而不是A,故C错误;
5、循环队列放在一维数组A[0…M-1]中,end1指向队头元素,end2指向队尾元素的后一个位置。假设队列两端均可进行入队和出队操作,队列中最多能容纳M-1个元素。初 始时为空,下列判断队空和队满的条件中,正确的是()
A. 队空:end1==end2;队满:end1==(end2+1) mod M
B. 队空:end1==end2;队满:end2==(end1+1) mod (M-1)
C. 队空:end2==(end1+1) mod M;队满:end1==(end2+1) mod M
D. 队空:end1==(end2+1) mod M;队满:end2==(end1+1) mod (M-1)
正确答案:A
题解:
两个下标在相同位置时为空,队尾+1模上空间大小等于队头等于满;故选A;
6、已知二叉树后序遍历序列是bfegcda,中序遍历序列是badefcg,它的前序遍历序列是()
A. abcdefg
B. abdcefg
C. adbcfeg
D. abecdfg
正确答案:B
题解:
我们每次可通过后序确定一个根,并在中序中分割左右子树;具体分析如下;

7、某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为()
A. 不存在这样的二叉树
B. 200
C. 198
D. 199
正确答案:A
题解:
公式,n0 = n2 + 1;计算得出200;
8、设有一组记录的关键字为{19,14,23,1,68,20,84,27,55,11,10,79},用链地址法构造哈希表,哈希函数为H(key)=key MOD 13,哈希地址为1的链中有()个记录
A. 1
B. 2
C. 3
D. 4
正确答案:D
题解:
题目即让我们求得上述哪些数据模13等于1;分别为1,14,27,79;故选D;
9、以下哪种排序是不稳定排序()
A. 冒泡
B. 插入排序
C. 归并排序
D. 快速排序
正确答案:D
题解:
快排无法保证排序的稳定性;
四、编程题题解
1、汽水瓶
思路:我们模拟喝汽水的过程,我们创建一个变量记录当前瓶子个数,一个变量记录总共喝了多少瓶;然后模拟喝汽水过程求解;
#include <iostream>
using namespace std;int main()
{int n;while(cin >> n){if(n == 0)break;// 记录当前瓶子个数int botton = n;int water = 0;while(botton >= 3){// 可以兑换汽水数water += botton / 3;// 求得喝完以后的瓶子数botton = botton % 3 + botton / 3;}// 处理特殊情况,借瓶子if(botton == 2)water += 1;cout << water << endl;}return 0;
}2、查找两个字符串a,b中的最长公共子串
思路:此题建议使用动态规划来做,找到以i-1结尾的str1与str2最大连续字符的个数;
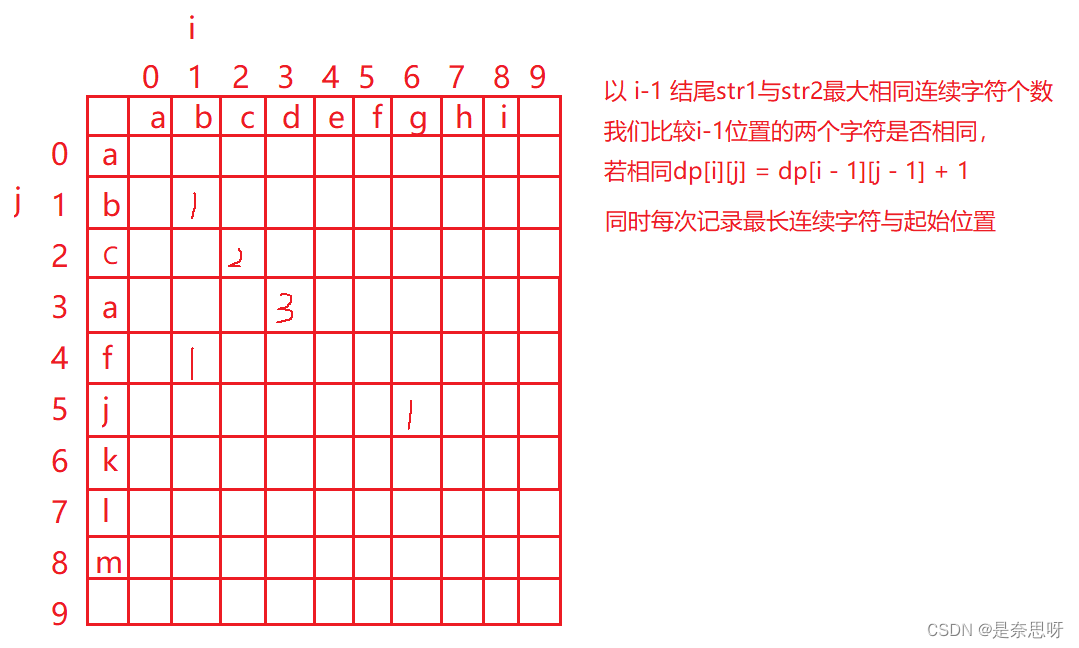
#include <iostream>
#include <string>
#include <vector>
using namespace std;string LComSub(string& str1, string& str2)
{int len1 = str1.size();int len2 = str2.size();// 多开一个位置vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));int start = 0;int max = 0;for(int i = 1; i <= len1; i++){for(int j = 1; j <= len2; j++){if(str1[i - 1] == str2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;if(dp[i][j] > max){max = dp[i][j];start = i - max;}}}return str1.substr(start, max);
}int main()
{string str1, str2;cin >> str1 >> str2;// 最短字符串放在str1中if(str1.size() > str2.size())str1.swap(str2);cout << LComSub(str1, str2) << endl;
}相关文章:

备战秋招 | 笔试强训19
目录 一、选择题 二、编程题 三、选择题题解 四、编程题题解 一、选择题 1、二分查找的时间复杂度() A. O(N*log(N)) B. O(N) C. O(log(N)) D. O(N^2) 2、有一个单向链表中有一个A、B两个相邻元素,有一个指针p指向元素A,现将…...

第一章 计算机网络概述
第一章 计算机网络概述 1.1 计算机网络在信息时代的作用 1.2 因特网概述 网络分类: 网络:许多计算机连接在一起的的局域网; 互联网:internet许多网络连接在一起; 因特网:Internet 全球最大的互联网&…...
谷粒商城第六天-商品服务之分类管理下的获取三级分类树形列表
目录 一、总述 1.1 前端思路 1.2 后端思路 二、前端部分 2.1 在网页中建好目录及菜单 2.1.1 建好商品目录 2.1.2 建好分类管理菜单 编辑 2.2 编写组件 2.2.1 先完成组件文件的创建 2.2.2 编写组件 2.2.2.1 显示三级分类树形列表 三、后端部分 3.1 编写商品分类…...
【UI自动化测试】Appium+Python+Unittest+HTMLRunner
简介 获取AppPackage和AppActivity 定位UI控件的工具 脚本结构 PageObject分层管理 HTMLTestRunner生成测试报告 启动appium server服务 以python文件模式执行脚本生成测试报告 【B站最通俗易懂】Python接口自动化测试从入门到精通,超详细的进阶教程,看完…...

【限时优惠】红帽openstack管理课程(CL210) 即将开课
课程介绍 通过实验室操作练习,学员将能够深入学习红帽企业 Linux OpenStack 平台各服务的手动安装方法,还将了解 OpenStack 开发社区的未来发展计划。 培训地点: 线下面授:苏州市姑苏区干将东路666号401室; 远程…...
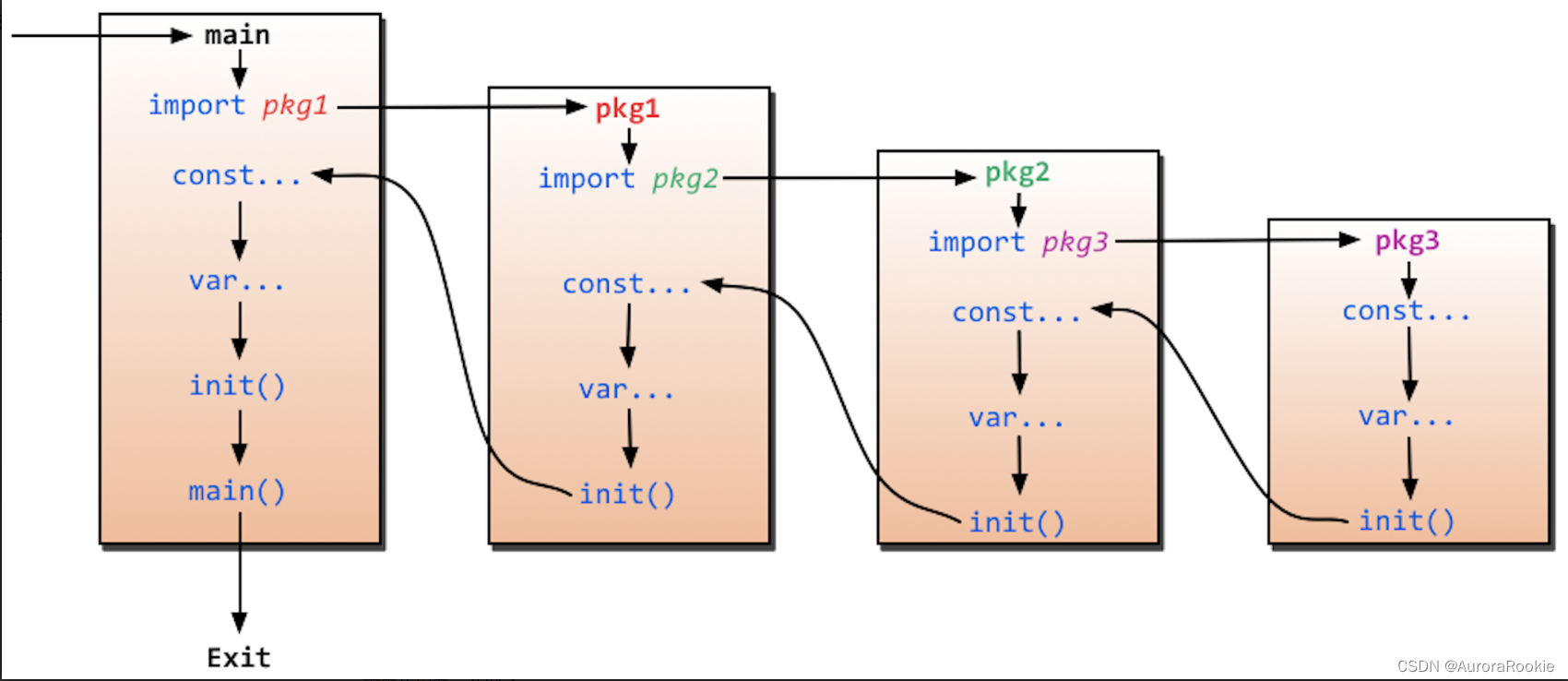
Golang之路---02 基础语法——函数
函数 函数定义 func function_name( [parameter list] ) [return_types] {函数体 }参数解释: func:函数由 func 开始声明function_name:函数名称,函数名和参数列表一起构成了函数签名。[parameter list]:参数列表&a…...
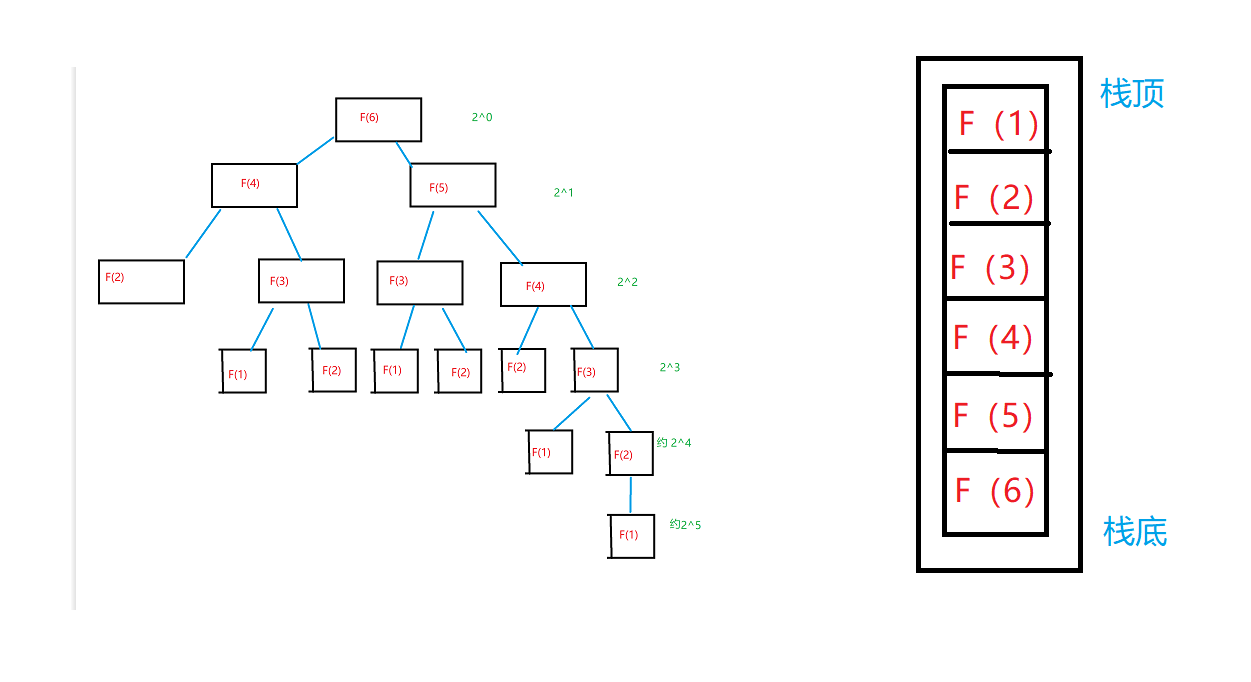
数据结构和算法入门(时间/空间复杂度介绍--java版)
数据结构和算法入门(时间/空间复杂度介绍–java版) write in front 作者: 向大佬学习 专栏: 数据结构(java版) 作者简介:大二学生 希望能学习其同学和大佬的经验! 本篇博客简介&…...
—官方原版)
Spring Mvc 文件上传(MultipartFile )—官方原版
一、创建应用程序类 要启动Spring Boot MVC应用程序,首先需要一个启动器。在这个示例中,已经添加了spring-boot-starter thymelaf和spring-boot-starter web作为依赖项。要使用Servlet容器上传文件,您需要注册一个MultipartConfigElement类&…...

【E题】2023年电赛运动目标控制与自动追踪系统方案
系统的设计和制作可以按照以下步骤进行: 设计红色光斑位置控制系统: 选择合适的红色激光笔,并将其固定在一个二维电控云台上。 使用电机和编码器来控制电控云台的水平和垂直运动。 设计一个控制电路,可以通过输入控制信号来控制…...

企业网络安全之零信任和身份认证
零信任并不是一种技术,而是一个安全概念,是一种建立安全战略的理念、方法和框架。 零信任提供了一系列概念和思想,其中心思想是怀疑一切,否定一切,不再以网络边界为限,不能再将内部网络定义为可信任的&…...

【雕爷学编程】MicroPython动手做(28)——物联网之Yeelight 5
知识点:什么是掌控板? 掌控板是一块普及STEAM创客教育、人工智能教育、机器人编程教育的开源智能硬件。它集成ESP-32高性能双核芯片,支持WiFi和蓝牙双模通信,可作为物联网节点,实现物联网应用。同时掌控板上集成了OLED…...

[运维|中间件] 东方通TongWeb使用笔记
参考文献 东方通tongweb部署服务 东方通tongweb部署服务 使用笔记 默认访问地址 http://ip:9060/console/默认用户名密码 TongWeb7.0默认用户名密码:thanos,thanos123.com...
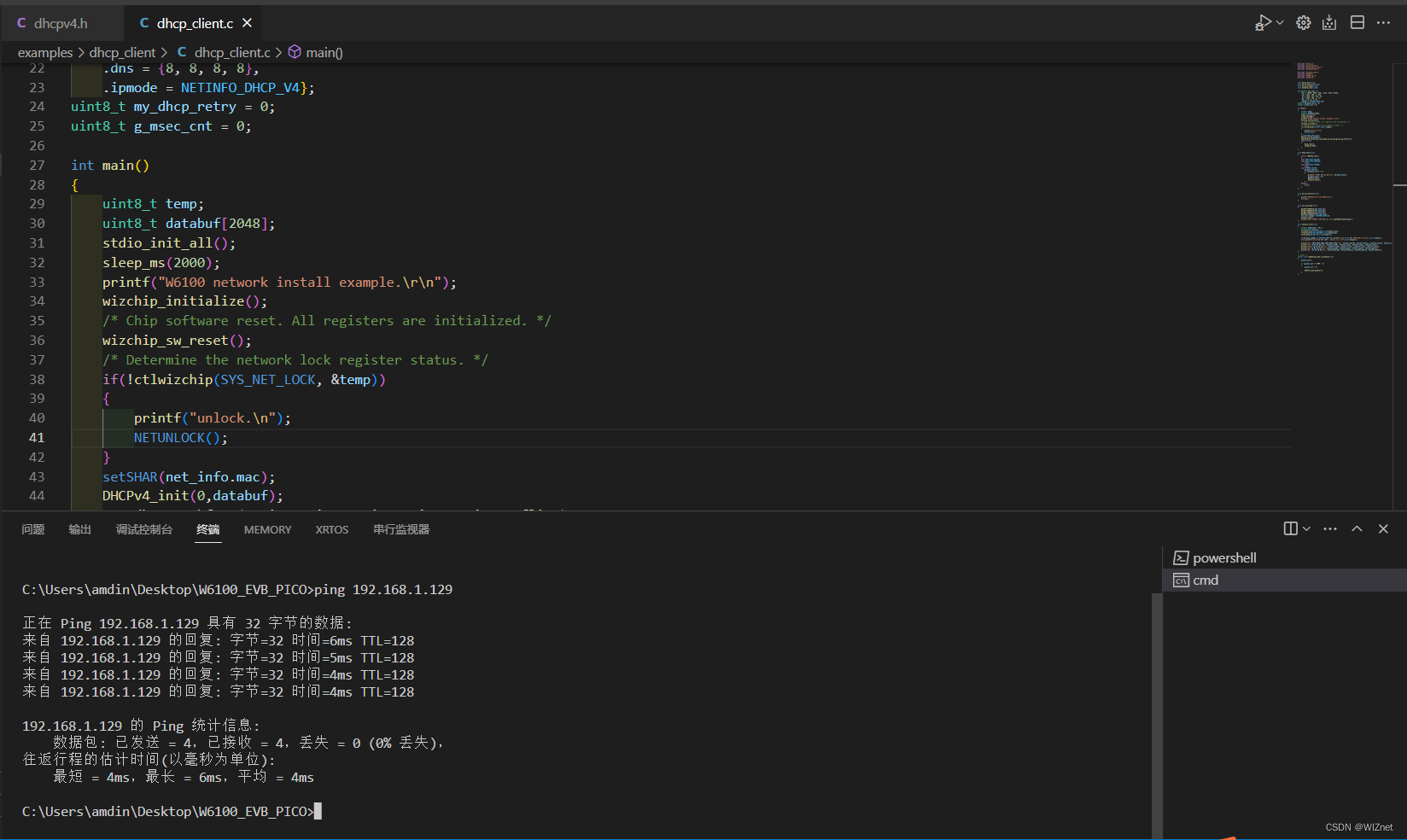
WIZnet W6100-EVB-Pico DHCP 配置教程(三)
前言 在上一章节中我们讲了网络信息配置,那些网络信息的配置都是用户手动的去配置的,为了能跟电脑处于同一网段,且电脑能成功ping通板子,我们不仅要注意子网掩码,对于IP地址主机位和网络位的划分,而且还要注…...

【Linux】Ansible 脚本 playbook 剧本
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 Ansible 脚本 playbook 剧本 playbook 剧本Templates 模块tags 模块Roles 模块在一个 playbook 中使用 roles 的步骤 playbook 剧本 playbooks 本身由以下各部分组成 &#…...

解决 tensorflow 出现的 ImportError: Could not find the DLL(s) ‘msvcp140_1.dll‘. 问题
在安装完tensorflow库后出现 问题详述: ImportError: Could not find the DLL(s) msvcp140_1.dll. TensorFlow requires that these DLLs be installed in a directory that is named in your %PATH% environment variable. You may install these DLLs by downlo…...
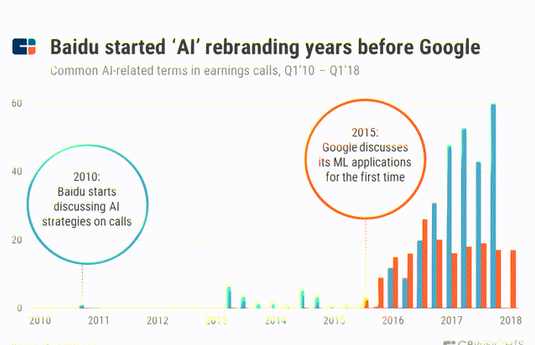
百度与AI:历史、投资和监管
来源:猛兽财经 作者:猛兽财经 百度的人工智能在中国具有先发优势 随着ChatGPT的爆火,人工智能重新引起了投资者的注意,然而人工智能并不是突然爆火的,而是全球众多公司在人工智能技术上进行数十年如一日的研发和积累&a…...

Kafka3.0.0版本——Broker(Zookeeper服务端存储的Kafka相关信息)
目录 一、启动zookeeper集群及kafka集群服务启动1.1、先启动三台zookeeper集群服务,再启动三台kafka集群服务1.2、使用PrettyZoo连接zookeeper客户端工具 二、在zookeeper服务端存储的Kafka相关信息 一、启动zookeeper集群及kafka集群服务启动 1.1、先启动三台zook…...
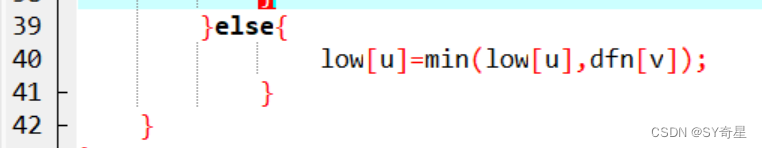
【图论】无向图连通性(tarjan算法)
割边:dfn[u]<low[v] 割点:dfn[u]<low[v] (若为根节点,要有两个v这样的点) 一.知识点: 1.连通: 在图论中,连通性是指一个无向图中的任意两个顶点之间存在路径。如果对于图中的任意两个顶点 u 和 v&…...

Docker安装
Docker实践 yum安装 YUM源可以使用官方YUM源、清华大学开源镜像站配置YUM源,也可以使用阿里云开源镜像站提供的YUM源,建议选择使用阿里云开源镜像站提供的YUM源,原因速度快。 地址: https://developer.aliyun.com/mirror/ 我们安装ce版 …...

06. 计数原理
6. 计数原理 6.1 分类加法计数原理与分步乘法计数原理 分类加法计数原理定义 完成一件事,有 n n n 类办法,在第1类办法中有 m 1 m_1 m1 种不同的方法,在第2类办法中有 m 2 m_2 m2 种不同的方法,…,在第 n n…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...
