06. 计数原理
6. 计数原理
6.1 分类加法计数原理与分步乘法计数原理
分类加法计数原理定义
完成一件事,有 n n n 类办法,在第1类办法中有 m 1 m_1 m1 种不同的方法,在第2类办法中有 m 2 m_2 m2 种不同的方法,…,在第 n n n 类办法中有 m n m_n mn 种不同的方法,那么完成这件事共有 N = m 1 + m 2 + . . . + m n N = m_1 + m_2 + ... + m_n N=m1+m2+...+mn 种不同的方法。
分步乘法计数原理定义
完成一件事,需要分成 n n n 个步骤,做第1步有 m 1 m_1 m1 种不同的方法,做第2步有 m 2 m_2 m2 种不同的方法,…,做第 n n n 步有 m n m_n mn种不同的方法,那么完成这件事共有: N = m 1 ⋅ m 2 ⋅ … ⋅ m n N=m_1 \cdot m_2 \cdot \ldots \cdot m_n N=m1⋅m2⋅…⋅mn种不同的方法。
总结:如果完成一件事的各种方法是相互独立的,那么计算完成这件事的方法数时,使用分类计数原理。如果完成一件事的各个步骤是相互联系的,即各个步骤都必须完成,这件事才能完成,那么计算完成这件事的方法数时,使用分步计数原理。
-
高二年级一班有女生18人,男生38人,从中选取一名学生作代表,参加学校组织的调查团,选取代表的方法有几种?
-
若 a a a、 b b b 是正整数,且 a + b ≤ 6 a+b≤6 a+b≤6,则以 ( a , b ) (a,b) (a,b) 为坐标的点共有多少个?
-
用0到9这10个数字,可以组成没有重复数字的三位偶数的个数为( )。
A.324
B.328
C.360
D.648 -
用数字1,2,3,4,5组成的无重复数字的四位偶数的个数为 ( )。
A.8
B.24
C.48
D.120 -
将3个不同的小球放入4个盒子中,则不同放法种数有多少种?
-
如果在一周内(周一至周日)安排三所学校的学生参观某展览馆,每天最多只安排一所学校,要求甲学校连续参观两天,其余两所学校均只参观一天,那么不同的安排方法共有多少种?
-
用0,1,2,3,4,5这6个数字:
(1)可以组成多少个数字不重复的三位数。
(2)可以组成多少个数字允许重复的三位数。 -
(1)六名同学报名参加三项体育比赛,每人限报一项,共有多少种不同的报名结果?
(2)六名同学参加三项比赛,三个项目比赛冠军的不同结果有多少种? -
用0,3,4,5,6排成无重复字的五位数,要求偶数字相邻,奇数字也相邻,则这样的五位数的个数是?
-
若自然数 n n n 使得作竖式加法 n + ( n + 1 ) + ( n + 2 ) n+(n+1)+(n+2) n+(n+1)+(n+2) 均不产生进位现象。则称 n n n 为“可连数”。例如:32是“可连数”,因32+33+34不产生进位现象;23不是“可连数”,因23+24+25产生进位现象。那么,小于1000的“可连数”的个数为( )
A.27
B.36
C.39
D.48 -
用0,1,2,3,4,5这6个数字,可以组成多少个大于3000,小于5421的数字不重复的四位数。
-
同室4人各写1张贺年卡,先集中起来,然后每人从中各拿1张别人送出的贺年卡,则4张贺年卡不同的分配方式有( )
A.6种
B.9种
C.11种
D.23种 -
某班新年联欢会原定的6个节目已排成节目单,开演前又增加了3个新节目,如果将这3个节目插入原节目单中,那么不同的插法种数为( )
A.504
B.210
C.336
D.120
6.2 排列与组合
排列数的定义
从 n n n 个不同元素中取出 m ( m ⩽ n ) m(m \leqslant n) m(m⩽n) 个元素排成一列,叫做从 n n n 个不同元素中取出 m m m 个元素的一个排列。
从 n n n 个不同元素中取出 m ( m ⩽ n ) m(m \leqslant n) m(m⩽n) 个元素的所有排列的个数,叫做从 n n n 个不同元素中取出 m m m 个元素的排列数,用符号 A n m A_n^m Anm 表示。
排列数的公式
A n m = n ( n − 1 ) ( n − 2 ) … ( n − m + 1 ) = n ! ( n − m ) ! A_n^m = n(n-1)(n-2) \ldots (n-m+1) = \dfrac{n!}{(n-m)!} Anm=n(n−1)(n−2)…(n−m+1)=(n−m)!n!
当 m = n m = n m=n 时, A n m = n ! = n ( n − 1 ) ( n − 2 ) … 3 ⋅ 2 ⋅ 1 A_n^m = n! = n(n-1)(n-2) \ldots 3 \cdot 2 \cdot 1 Anm=n!=n(n−1)(n−2)…3⋅2⋅1
0 ! = 1 0! = 1 0!=1
排列数的性质
- A n m = n A n − 1 m − 1 A_n^m = nA_{n-1}^{m-1} Anm=nAn−1m−1
- A n m = 1 n − m A n m + 1 = n n − m A n − 1 m A_n^m = \dfrac{1}{n-m}A_n^{m+1}=\dfrac{n}{n-m}A_{n-1}^m Anm=n−m1Anm+1=n−mnAn−1m
- A n m = m A n − 1 m − 1 + A n − 1 m A_n^m = mA_{n-1}^{m-1} + A_{n-1}^{m} Anm=mAn−1m−1+An−1m
组合数定义
从 n n n 个不同元素中取出 m ( m ⩽ n ) m(m \leqslant n) m(m⩽n) 个元素并成一组,叫做从 n n n 个不同元素中取出 m m m 个元素的一个组合。
从 n n n 个不同元素中取出 m ( m ⩽ n ) m(m \leqslant n) m(m⩽n) 个元素的所有组合的个数,叫做从 n n n 个不同元素中取出 m m m 个元素的组合数,用符号 C n m C_n^m Cnm 表示。
组合数公式及其推导
求从 n n n 个不同元素中取出 m m m 个元素的排列数 A n m A_n^m Anm,可以按以下两步来考虑:
第一步,先求出从这 n n n 个不同元素中取出 m m m 个元素的组合数 C n m C_n^m Cnm;
第二步,求每一个组合中 m m m 个元素的全排列数 A m m A_m^m Amm;
根据分步计数原理,得到 A n m = C n m ⋅ A m m A_n^m = C_n^m \cdot A_m^m Anm=Cnm⋅Amm,
因此 C n m = A n m A m m = n ( n − 1 ) ( n − 2 ) … ( n − m + 1 ) m ! C_n^m = \dfrac{A_n^m}{A_m^m}=\dfrac{n(n-1)(n-2) \ldots (n-m+1)}{m!} Cnm=AmmAnm=m!n(n−1)(n−2)…(n−m+1)
这里 n , m ∈ N + n,m \in N_+ n,m∈N+,且 m ⩽ n m \leqslant n m⩽n,这个公式叫做组合数公式。
因为 A n m = n ! ( n − m ) ! A_n^m=\dfrac{n!}{(n-m)!} Anm=(n−m)!n!,所以组合数公式还可表示为 C n m = n ! m ! ( n − m ) ! C_n^m = \dfrac{n!}{m!(n-m)!} Cnm=m!(n−m)!n!
C n 0 = C n n = 1 C_n^0 = C_n^n = 1 Cn0=Cnn=1
组合数的性质
- C n m = C n n − m C_n^m = C_n^{n-m} Cnm=Cnn−m
- C n m + C n m − 1 = C n + 1 m C_n^m + C_n^{m-1} = C_{n+1}^m Cnm+Cnm−1=Cn+1m
排列组合的综合应用
- 列举法
- 情况较少。当涉及对象数目不大时,一般选用列举法、树形图法、图表法或者框图法。
-
(无限制条件的排列问题)利用1,2,3,4这四个数字,可以组成多少个没有重复数字的三位数?
-
(元素相邻问题)记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( )
A.1440种
B.720种
C.960种
D.480种 -
某人射击8枪,命中4枪,4枪命中恰好有3枪连在一起的不同种数为多少?
-
(元素不相邻问题)《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味。若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A.288种
B.144种
C.720种
D.360种 -
一个晚会的节目有4个舞蹈,2个相声,3个独唱,舞蹈节目不能连续出场,则节目的出场顺序有多少种?
-
(定位、定元问题)6名同学排成1排照相,要求同学甲既不站在最左边又不站在最右边,共有多少种不同站法?
-
(无限制条件的组合问题)从5种主料中选2种,8种辅料中选3种来烹饪一道菜,烹饪方式有5种,那么最多可以烹饪出不同的菜的种数为( )
A.18
B.200
C.2800
D.33600 -
(有限制条件的组合问题)某医院从10名医疗专家中抽调6名赴灾区救灾,其中这10名医疗专家中有4名是外科专家。问:
(1)抽调的6名专家中恰有2名是外科专家的抽调方法有多少种?
(2)至少有2名外科专家的抽调方法有多少种?
(3)至多有2名外科专家的抽调方法有多少种? -
三人互相传球,由甲开始发球,并作为第一次传球,经过5次传球后,球仍回到甲手中,则不同的传球方式共有( )
A. 5种
B. 10种
C. 8种
D. 16种 -
设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入这五个盒子内,要求每个盒子内放一个球,并且恰好有一个球的编号与盒子的编号相同,则这样的投放方法的总数为?
-
有红、黄、蓝色的球各5只,分别标有A、B、C、D、E五个字母,现从中取5只,要求各字母均有且三色齐备,则共有多少种不同的取法?
6.3 二项式定理
二项式定理定义
一般地,对于任意正整数 n n n,都有 ( a + b ) n = C n 0 a n + C n 1 a n − 1 b + … + C n r a n − r b r + … + C n n b n ( n ∈ N ∗ ) (a+b)^n = C_n^0a^n + C_n^1a^{n-1}b + \ldots + C_n^ra^{n-r}b^r + \ldots + C_n^nb^n (n \in N*) (a+b)n=Cn0an+Cn1an−1b+…+Cnran−rbr+…+Cnnbn(n∈N∗) 这个公式所表示的定理叫做二项式定理,等号右边的多项式叫做 ( a + b ) n (a+b)^n (a+b)n 的二项展开式。
式中的 C n r a n − r b r C_n^ra^{n-r}b^{r} Cnran−rbr 叫做二项展开式的通项, 用 T r + 1 T_{r+1} Tr+1 表示,即通项为展开式的第 r + 1 r+1 r+1 项: T r + 1 = C n r a n − r b r T_{r+1} = C_n^ra^{n-r}b^r Tr+1=Cnran−rbr,其中的系数 C n r ( r = 0 , 1 , 2 , … , n ) C_n^r (r=0,1,2, \ldots ,n) Cnr(r=0,1,2,…,n) 叫做二项式系数。
二项式 ( a + b ) n (a+b)^n (a+b)n 的展开式的特点
- 项数:共有 n + 1 n+1 n+1 项,比二项式的次数大1;
- 二项式系数:第 r + 1 r+1 r+1 项的二项式系数为 C n r C_n^r Cnr,最大二项式系数项居中;
- 次数:各项的次数都等于二项式的幂指数 n n n。字母 a a a 降幂排列,次数由 n n n 到 0;字母 b b b 升幂排列,次数从0到 n n n,每一项中, a , b a,b a,b 次数和均为 n n n;
- 项的系数:二项式系数依次是 C n 0 , C n 1 , C n 2 , … , C n r , … , C n n C_n^0,C_n^1,C_n^2,\ldots,C_n^r,\ldots ,C_n^n Cn0,Cn1,Cn2,…,Cnr,…,Cnn,项的系数是 a a a 与 b b b 的系数(包括二项式系数)。
两个常用的二项展开式
- ( a − b ) n = C n 0 a n − C n 1 a n − 1 b + … + ( − 1 ) r ⋅ C n r a n − r b r + … + ( − 1 ) n ⋅ C n n b n ( n ∈ N ∗ ) (a-b)^n = C_n^0a^n - C_n^1a^{n-1}b + \ldots + (-1)^r \cdot C_n^ra^{n-r}b^r + \ldots +(-1)^n \cdot C_n^nb^n (n \in N^*) (a−b)n=Cn0an−Cn1an−1b+…+(−1)r⋅Cnran−rbr+…+(−1)n⋅Cnnbn(n∈N∗)
- ( 1 + x ) n = 1 + C n 1 x + C n 2 x 2 + … + C n r x r + … + x n (1+x)^n = 1 + C_n^1x + C_n^2x^2 + \ldots + C_n^rx^r + \ldots + x^n (1+x)n=1+Cn1x+Cn2x2+…+Cnrxr+…+xn
二项展开式的通项公式
T r + 1 = C n r a n − r b r ( r = 0 , 1 , 2 , … , n ) T_{r+1} = C_n^ra^{n-r}b^r(r=0,1,2, \ldots ,n) Tr+1=Cnran−rbr(r=0,1,2,…,n)
公式特点:
- 它表示二项展开式的第 r + 1 r+1 r+1 项,该项的二项式系数是 C n r C_n^r Cnr;
- 字母 b b b 的次数和组合数的上标相同;
- a a a 与 b b b 的次数之和为 n n n。
相关文章:

06. 计数原理
6. 计数原理 6.1 分类加法计数原理与分步乘法计数原理 分类加法计数原理定义 完成一件事,有 n n n 类办法,在第1类办法中有 m 1 m_1 m1 种不同的方法,在第2类办法中有 m 2 m_2 m2 种不同的方法,…,在第 n n…...
计算机网络基础(静态路由,动态路由,公网IP,私网IP,NAT技术)
文章目录 一:静态路由和动态路由二:静态路由的配置路由信息的方式演示三:默认路由四:公网IP和私网IP和NAT技术的基本理解 一:静态路由和动态路由 在说静态路由和动态路由前,我们需要来了解一下࿰…...

CGAL 点云Alpha-Shape曲面重建算法
文章目录 一、简介二、相关参数三、实现代码四、实现效果参考资料一、简介 在数学上, a l p h a − s h a p e alpha-shape a...

Java 文件过滤器FileFilter | 按条件筛选文件
文章目录 一、概述1.1 何时会用到文件过滤器1.2 工作流程1.3 常用的接口和类1.4 文件过滤器的作用 二、按文件属性过滤2.1 按前缀或后缀过滤文件名2.2 按文件大小过滤 三、按文件内容过滤3.1 文本文件过滤器3.1.1 根据关键字过滤文件内容3.1.2 使用正则表达式过滤文件内容 3.2 …...

python格式化地址信息
背景 最近在折腾一个好玩的库,capa 实现地址的格式化输出。我看的教程是这样的: location_str ["徐汇区虹漕路461号58号楼5楼", "泉州市洛江区万安塘西工业区"] import cpca df cpca.transform(location_str) df在正式的运行代码…...

k8s1.26.6 安装gitlab
Gitlab官方提供了 Helm 的方式在 Kubernetes 集群中来快速安装,但是在使用的过程中发现 Helm 提供的 Chart 包中有很多其他额外的配置,所以我们这里使用自定义的方式来安装,也就是自己来定义一些资源清单文件。 Gitlab主要涉及到3个应用&…...
C5.0决策树建立个人信用风险评估模型
通过构建自动化的信用评分模型,以在线方式进行即时的信贷审批能够为银行节约很多人工成本。本案例,我们将使用C5.0决策树算法建立一个简单的个人信用风险评估模型。 导入类库 读取数据 #创建编码所用的数据字典 col_dicts{} #要编码的属性集 cols [che…...
)
【k8s集群部署】使用containerd运行时部署kubernetes集群(V1.27版本)
【k8s集群部署】使用containerd运行时部署kubernetes集群(V1.27版本) 一、本次实践介绍1.1 环境规划介绍1.2 本次实践简介二、三台主机基础环境配置2.1 主机配置工作2.2 关闭防火墙和selinux2.3 关闭swap2.4 清空iptables2.5 配置时间同步2.6 修改内核参数2.7 配置hosts文件三…...

网络安全进阶学习第八课——信息收集
文章目录 一、什么是信息收集?二、信息收集的原则三、信息收集的分类1.主动信息收集2.被动信息收集 四、资产探测1、Whois查询#常用网站: 2、备案信息查询#常用网站: 3、DNS查询#常用网站: 4、子域名收集#常用网站:#常…...

Spring Data Elasticsearch - 在Spring应用中操作Elasticsearch数据库
Spring Data Elasticsearch 文章目录 Spring Data Elasticsearch1. 定义文档映射实体类2. Repository3. ElasticsearchRestTemplate3.1 查询相关特性3.1.1 过滤3.1.2 排序3.1.3 自定义分词器 3.2 高级查询 4. 索引管理4.1 创建索引4.2 检索索引4.3 修改映射4.4 删除索引 5. 异常…...
图论-简明导读
计算机图论是计算机科学中的一个重要分支,它主要研究图的性质和结构,以及如何在计算机上有效地存储、处理和操作这些图。本文将总结计算机图论的核心知识点。 一、基本概念 计算机图论中的基本概念包括图、节点、边等。图是由节点和边构成的数据结构&am…...
记一次 .NET 某物流API系统 CPU爆高分析
一:背景 1. 讲故事 前段时间有位朋友找到我,说他程序CPU直接被打满了,让我帮忙看下怎么回事,截图如下: 看了下是两个相同的程序,既然被打满了那就抓一个 dump 看看到底咋回事。 二:为什么会打…...
【Docker】Docker安装Kibana服务_Docker+Elasticsearch+Kibana
文章目录 1. 什么是Kibana2. Docker安装Kibana2.1. 前提2.2. 安装Kibana 点击跳转:Docker安装MySQL、Redis、RabbitMQ、Elasticsearch、Nacos等常见服务全套(质量有保证,内容详情) 1. 什么是Kibana Kibana 是一款适用于Elasticse…...

前端面试题-VUE
1. 对于MVVM的理解 MVVM 是 Model-View-ViewModel 的缩写Model 代表数据模型,也可以在 Model 中定义数据修改和操作的业务逻辑。View 代表 UI 组件,它负责将数据模型转化成 UI 展现出来。ViewModel 监听模型数据的改变和控制视图⾏为、处理⽤户交互&…...

Linux嵌入式平台安全启动理解介绍
一、意义 安全启动可以防止未授权的或是进行恶意篡改的软件在系统上运行,是系统安全的保护石,每一级的前一个镜像会对该镜像进行校验。 1.1 安全启动原理介绍 通过数字签名进行镜像完整性验证(使用到非对称加密算法和哈希算法) 签名过程: raw_image--->use ha…...
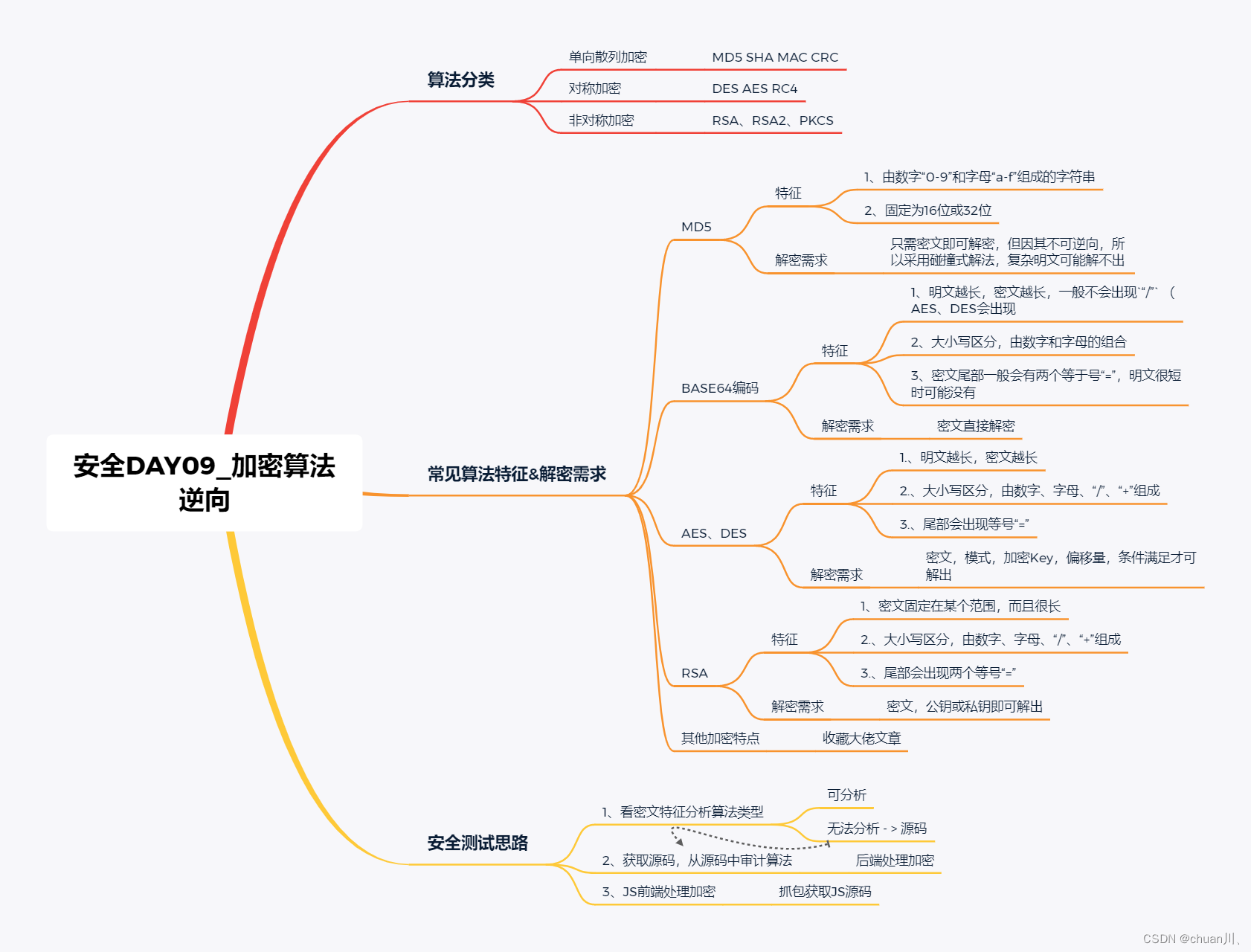
安全学习DAY09_加密逆向,特征识别
算法逆向&加密算法分类,特征识别 文章目录 算法逆向&加密算法分类,特征识别算法概念,分类单向散列加密 - MD5对称加密 - AES非对称加密 - RSA 常见加密算法识别特征,解密特点MD5密文特点BASE64编码特点AES、DES特点RSA密文…...
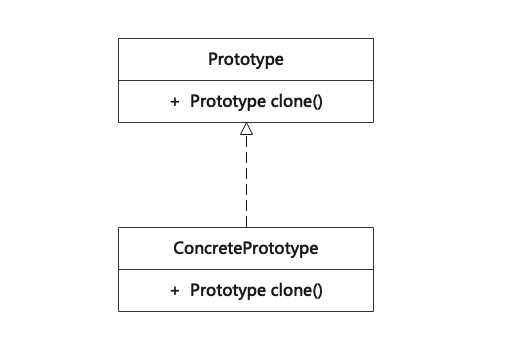
原型模式(Prototype)
原型模式是一种创建型设计模式,使调用方能够复制已有对象,而又无需使代码依赖它们所属的类。当有一个类的实例(原型),并且想通过复制原型来创建新对象时,通常会使用原型模式。 The Prototype pattern is g…...
深度学习之用PyTorch实现线性回归
代码 # 调用库 import torch# 数据准备 x_data torch.Tensor([[1.0], [2.0], [3.0]]) # 训练集输入值 y_data torch.Tensor([[2.0], [4.0], [6.0]]) # 训练集输出值# 定义线性回归模型 class LinearModel(torch.nn.Module):def __init__(self):super(LinearModel, self)._…...

45.248.11.X服务器防火墙是什么,具有什么作用
防火墙是一种网络安全设备或软件,服务器防火墙的作用主要是在服务器和外部网络之间起到一个安全屏障的作用,保护计算机网络免受未经授权的访问、恶意攻击或不良网络流量的影响,保护服务器免受恶意攻击和非法访问。它具有以下功能:…...
如何以无服务器方式运行 Go 应用程序
Go编程语言一直以来都对构建REST API提供了丰富的支持。这包括一个出色的标准库(net/HTTP),以及许多流行的包,如Gorilla mux、Gin、Negroni、Echo、Fiber等。使用AWS Lambda Go运行时,我们可以使用Go构建AWS Lambda函数…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
