【图论】无向图连通性(tarjan算法)
割边:dfn[u]<low[v]
割点:dfn[u]<=low[v] (若为根节点,要有两个v这样的点)
一.知识点:
1.连通:
在图论中,连通性是指一个无向图中的任意两个顶点之间存在路径。如果对于图中的任意两个顶点 u 和 v,存在一条路径从 u 到 v,那么图被称为连通图。如果图不是连通的,那么它可以被分为多个连通分量,每个连通分量都是一个连通子图。
2.割点:
割点(Cut Vertex),也称为关节点或割顶,是指在无向图中,如果移除该顶点及其相连的边,会导致图不再连通,那么该顶点就被称为割点。
3.割边:
割边(Cut Edge),也称为桥,是指在无向图中,如果移除该边,会导致图不再连通,那么该边就被称为割边。
割边在图中起到了连接不同连通分量的作用,其移除会导致图的连通性发生变化。
4.tarjan算法:(选择性阅读)
![]()
Tarjan算法是一种用于寻找有向图中强连通分量(Strongly Connected Components,简称SCC)的算法,由Robert Tarjan在1972年提出。强连通分量是指在有向图中,任意两个顶点之间存在双向路径。
Tarjan算法使用深度优先搜索(DFS)来遍历图,并通过维护一个栈和一些辅助数据结构来识别强连通分量。算法的基本思想是通过DFS遍历图中的每个顶点,并为每个顶点记录其访问次序(Discovery Time)和能够回溯到的最早的祖先顶点(Lowest Ancestor)。通过这些信息,可以识别出具有相同祖先的顶点集合,即一个强连通分量。
Tarjan算法的步骤如下:
- 对图中的每个顶点进行深度优先搜索(DFS)遍历。
- 在DFS遍历的过程中,为每个顶点记录其访问次序和最早祖先顶点。
- 将已访问的顶点入栈。
- 当DFS遍历回溯到一个顶点时,检查该顶点的最早祖先顶点。如果最早祖先顶点是自身,则将栈中的顶点弹出,并将这些顶点构成一个强连通分量。
- 重复步骤3和步骤4,直到遍历完所有的顶点。
Tarjan算法的时间复杂度为O(V+E),其中V是顶点数,E是边数。它是一种高效的算法,常被用于解决与强连通分量相关的问题,如图的缩点、强连通分量的数量和结构等。
总之,Tarjan算法是一种用于寻找有向图中强连通分量的算法,通过DFS遍历和栈的运用,可以高效地找到图中的所有强连通分量。
二.讲解
在此之前,先介绍两个数组;
int dfn[];里面存放访问顺序(时间戳);
int low[];里面存放追溯值(即祖先节点最小的dfn)
(1)割边
tarjan提出:(证明可以自行百度)
当dfn[u]<low[v]时,连接这两条点的边为割边(重边要特殊处理,后面介绍)
(2)割点
tarjan提出:(证明可以自行百度)
当dfn[u]<=low[v]时,u这个点为割点(若为根节点,要有两个v这样符合条件的点)
三.割边
(1)题目
题目描述:
找出割边
输入:
第一行输入两个整数n和m,表示点和边的个数。
第i(2<=i<=2+m)行,每行输出两个数字,表示一条边的两个点。
输出:
割边
样例输入:
6 7
1 2
1 3
2 4
2 5
3 4
4 5
4 6样例输出:
4---6
(2)初代码
/*
6 7
1 2
1 3
2 4
2 5
3 4
4 5
4 6
*/#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int n,m;
struct Edge{int u,v,next;
}edge[maxn<<1];
int cnt,head[maxn];
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]}; head[u]=cnt;
}
int num,dfn[maxn],low[maxn];
void tarjan(int u,int fa){dfn[u]=low[u]=++num;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(v==fa) continue;if(dfn[v]==0){tarjan(v,u);low[u]=min(low[u],low[v]);if(dfn[u]<low[v]){ //割边条件 ,若>则表示v不止和u相连 cout<<u<<"----"<<v<<endl; }}else{low[u]=min(low[u],dfn[v]);}}
}
int main(){scanf("%d%d",&n,&m);int u,v;for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);add(u,v); add(v,u);}tarjan(1,0);return 0;
}(3)bug与解答
1.若这张图有多个连通分量怎么办?
答:遍历即可
for(int i=1;i<=n;i++){if(dfn[i]==0) tarjan(1,0);}2.若有重边怎么办?结果显然不对。
答:只continue,第二次让这段代码运行
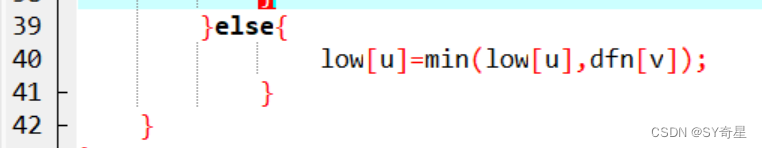
然后就无法满足 dfn[u]<low[v]条件了
if(v==fa){k++; //防止重边 if(k==1) continue;} (4)最终代码
/*
6 7
1 2
1 3
2 4
2 5
3 4
4 5
4 6
*/#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int n,m;
struct Edge{int u,v,next;
}edge[maxn<<1];
int cnt,head[maxn];
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]}; head[u]=cnt;
}
int num,dfn[maxn],low[maxn];
void tarjan(int u,int fa){int k=0;dfn[u]=low[u]=++num;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(v==fa){k++; //防止重边 if(k==1) continue;} if(dfn[v]==0){tarjan(v,u);low[u]=min(low[u],low[v]);if(dfn[u]<low[v]){ //割边条件 ,若>则表示v不止和u相连 cout<<u<<"---"<<v<<endl; }}else{low[u]=min(low[u],dfn[v]);}}
}
int main(){scanf("%d%d",&n,&m);int u,v;for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);add(u,v); add(v,u);}//防止本来就有不连通的 for(int i=1;i<=n;i++){if(dfn[i]==0) tarjan(1,0);}return 0;
}四.割点
其实只是微改动一下即可。其次就是可以优化一下。函数传参只需要传u,无需判断是否为父节点。因为不会影响结果。(自行参考代码推理)
再次强调:若为根节点,要有两个v这样的点!
参考代码:
/*
6 7
1 2
1 3
2 4
2 5
3 4
4 5
4 6
*/#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int n,m;
struct Edge{int u,v,next;
}edge[maxn<<1];
int cnt,head[maxn];
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]}; head[u]=cnt;
}
int num,dfn[maxn],low[maxn],root;
void tarjan(int u){dfn[u]=low[u]=++num;int flag=0;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(dfn[v]==0){tarjan(v);low[u]=min(low[u],low[v]);if(dfn[u]<=low[v]){ //割点条件 if(u!=root || flag>1) cout<<u<<" ";}}else{low[u]=min(low[u],dfn[v]);}}
}
int main(){scanf("%d%d",&n,&m);int u,v;for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);add(u,v); add(v,u);}//防止本来就有不连通的 for(int i=1;i<=n;i++){if(dfn[i]==0){root=i;tarjan(i);} }return 0;
}相关文章:
【图论】无向图连通性(tarjan算法)
割边:dfn[u]<low[v] 割点:dfn[u]<low[v] (若为根节点,要有两个v这样的点) 一.知识点: 1.连通: 在图论中,连通性是指一个无向图中的任意两个顶点之间存在路径。如果对于图中的任意两个顶点 u 和 v&…...

Docker安装
Docker实践 yum安装 YUM源可以使用官方YUM源、清华大学开源镜像站配置YUM源,也可以使用阿里云开源镜像站提供的YUM源,建议选择使用阿里云开源镜像站提供的YUM源,原因速度快。 地址: https://developer.aliyun.com/mirror/ 我们安装ce版 …...

06. 计数原理
6. 计数原理 6.1 分类加法计数原理与分步乘法计数原理 分类加法计数原理定义 完成一件事,有 n n n 类办法,在第1类办法中有 m 1 m_1 m1 种不同的方法,在第2类办法中有 m 2 m_2 m2 种不同的方法,…,在第 n n…...
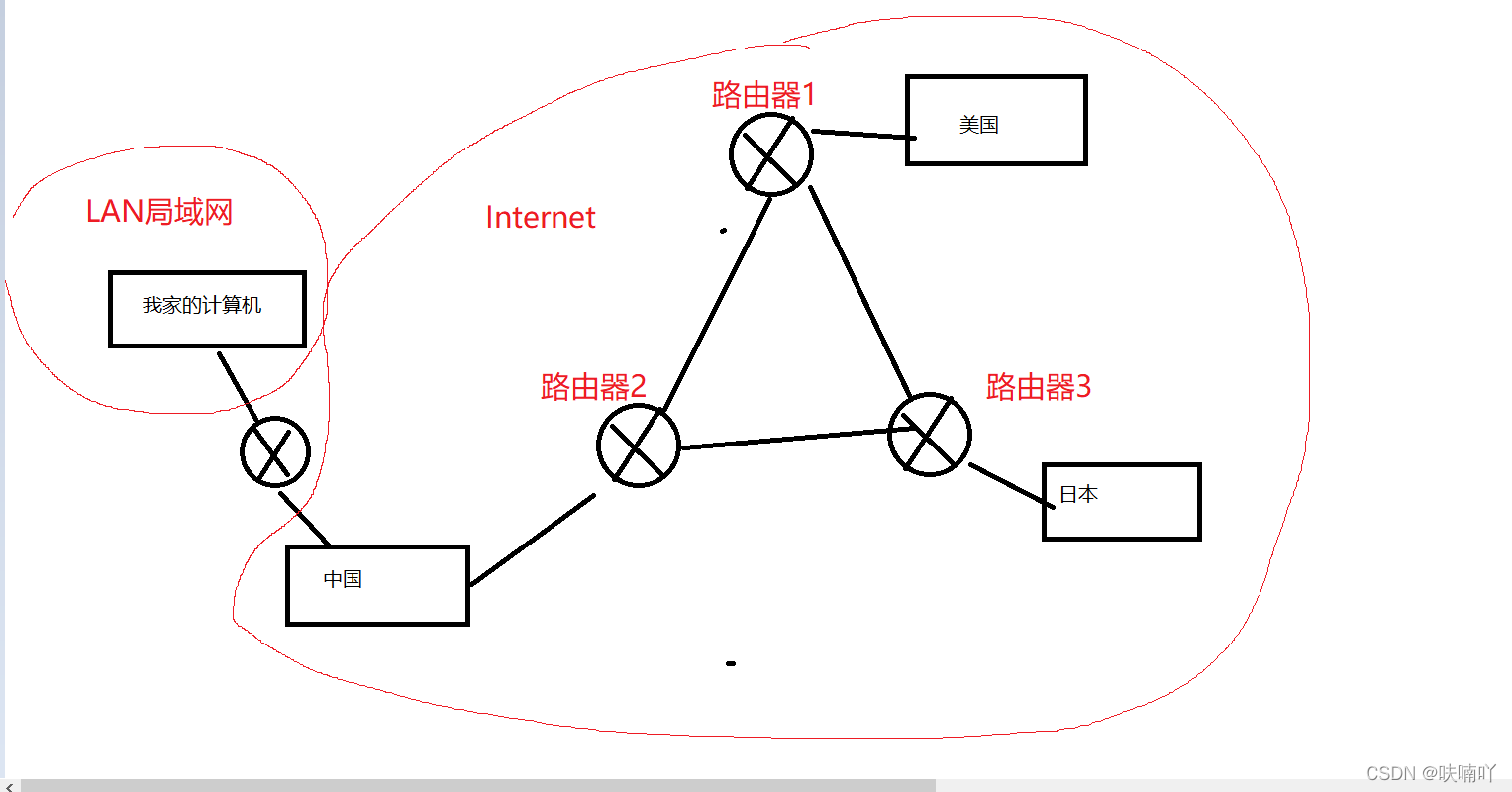
计算机网络基础(静态路由,动态路由,公网IP,私网IP,NAT技术)
文章目录 一:静态路由和动态路由二:静态路由的配置路由信息的方式演示三:默认路由四:公网IP和私网IP和NAT技术的基本理解 一:静态路由和动态路由 在说静态路由和动态路由前,我们需要来了解一下࿰…...

CGAL 点云Alpha-Shape曲面重建算法
文章目录 一、简介二、相关参数三、实现代码四、实现效果参考资料一、简介 在数学上, a l p h a − s h a p e alpha-shape a...

Java 文件过滤器FileFilter | 按条件筛选文件
文章目录 一、概述1.1 何时会用到文件过滤器1.2 工作流程1.3 常用的接口和类1.4 文件过滤器的作用 二、按文件属性过滤2.1 按前缀或后缀过滤文件名2.2 按文件大小过滤 三、按文件内容过滤3.1 文本文件过滤器3.1.1 根据关键字过滤文件内容3.1.2 使用正则表达式过滤文件内容 3.2 …...

python格式化地址信息
背景 最近在折腾一个好玩的库,capa 实现地址的格式化输出。我看的教程是这样的: location_str ["徐汇区虹漕路461号58号楼5楼", "泉州市洛江区万安塘西工业区"] import cpca df cpca.transform(location_str) df在正式的运行代码…...

k8s1.26.6 安装gitlab
Gitlab官方提供了 Helm 的方式在 Kubernetes 集群中来快速安装,但是在使用的过程中发现 Helm 提供的 Chart 包中有很多其他额外的配置,所以我们这里使用自定义的方式来安装,也就是自己来定义一些资源清单文件。 Gitlab主要涉及到3个应用&…...
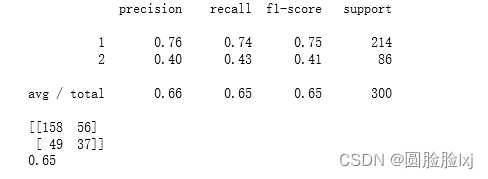
C5.0决策树建立个人信用风险评估模型
通过构建自动化的信用评分模型,以在线方式进行即时的信贷审批能够为银行节约很多人工成本。本案例,我们将使用C5.0决策树算法建立一个简单的个人信用风险评估模型。 导入类库 读取数据 #创建编码所用的数据字典 col_dicts{} #要编码的属性集 cols [che…...
)
【k8s集群部署】使用containerd运行时部署kubernetes集群(V1.27版本)
【k8s集群部署】使用containerd运行时部署kubernetes集群(V1.27版本) 一、本次实践介绍1.1 环境规划介绍1.2 本次实践简介二、三台主机基础环境配置2.1 主机配置工作2.2 关闭防火墙和selinux2.3 关闭swap2.4 清空iptables2.5 配置时间同步2.6 修改内核参数2.7 配置hosts文件三…...

网络安全进阶学习第八课——信息收集
文章目录 一、什么是信息收集?二、信息收集的原则三、信息收集的分类1.主动信息收集2.被动信息收集 四、资产探测1、Whois查询#常用网站: 2、备案信息查询#常用网站: 3、DNS查询#常用网站: 4、子域名收集#常用网站:#常…...

Spring Data Elasticsearch - 在Spring应用中操作Elasticsearch数据库
Spring Data Elasticsearch 文章目录 Spring Data Elasticsearch1. 定义文档映射实体类2. Repository3. ElasticsearchRestTemplate3.1 查询相关特性3.1.1 过滤3.1.2 排序3.1.3 自定义分词器 3.2 高级查询 4. 索引管理4.1 创建索引4.2 检索索引4.3 修改映射4.4 删除索引 5. 异常…...
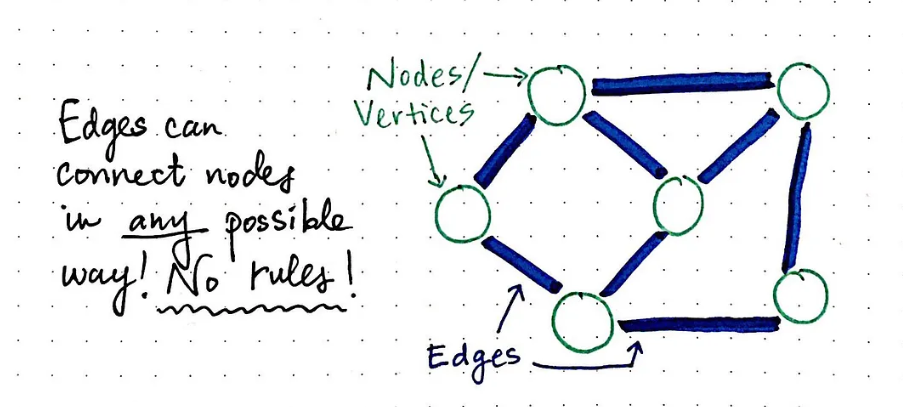
图论-简明导读
计算机图论是计算机科学中的一个重要分支,它主要研究图的性质和结构,以及如何在计算机上有效地存储、处理和操作这些图。本文将总结计算机图论的核心知识点。 一、基本概念 计算机图论中的基本概念包括图、节点、边等。图是由节点和边构成的数据结构&am…...
记一次 .NET 某物流API系统 CPU爆高分析
一:背景 1. 讲故事 前段时间有位朋友找到我,说他程序CPU直接被打满了,让我帮忙看下怎么回事,截图如下: 看了下是两个相同的程序,既然被打满了那就抓一个 dump 看看到底咋回事。 二:为什么会打…...
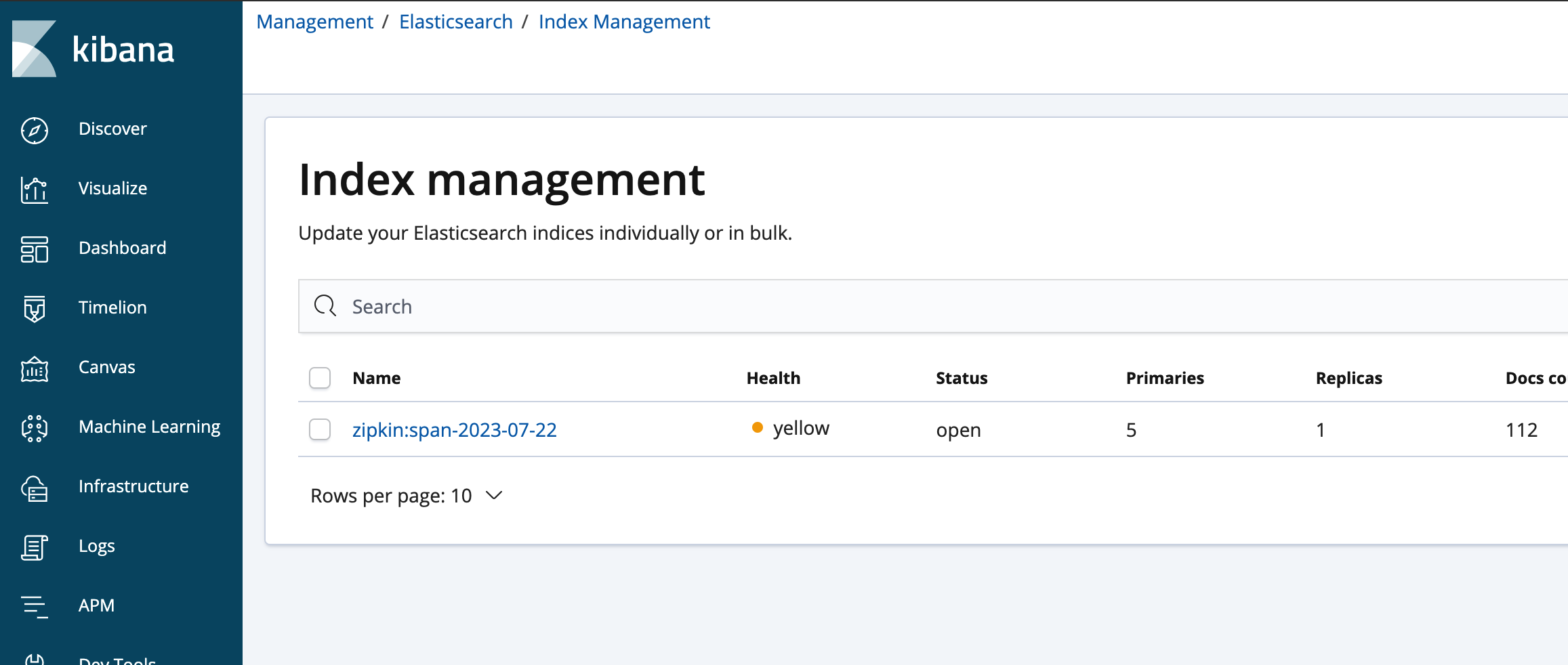
【Docker】Docker安装Kibana服务_Docker+Elasticsearch+Kibana
文章目录 1. 什么是Kibana2. Docker安装Kibana2.1. 前提2.2. 安装Kibana 点击跳转:Docker安装MySQL、Redis、RabbitMQ、Elasticsearch、Nacos等常见服务全套(质量有保证,内容详情) 1. 什么是Kibana Kibana 是一款适用于Elasticse…...

前端面试题-VUE
1. 对于MVVM的理解 MVVM 是 Model-View-ViewModel 的缩写Model 代表数据模型,也可以在 Model 中定义数据修改和操作的业务逻辑。View 代表 UI 组件,它负责将数据模型转化成 UI 展现出来。ViewModel 监听模型数据的改变和控制视图⾏为、处理⽤户交互&…...

Linux嵌入式平台安全启动理解介绍
一、意义 安全启动可以防止未授权的或是进行恶意篡改的软件在系统上运行,是系统安全的保护石,每一级的前一个镜像会对该镜像进行校验。 1.1 安全启动原理介绍 通过数字签名进行镜像完整性验证(使用到非对称加密算法和哈希算法) 签名过程: raw_image--->use ha…...
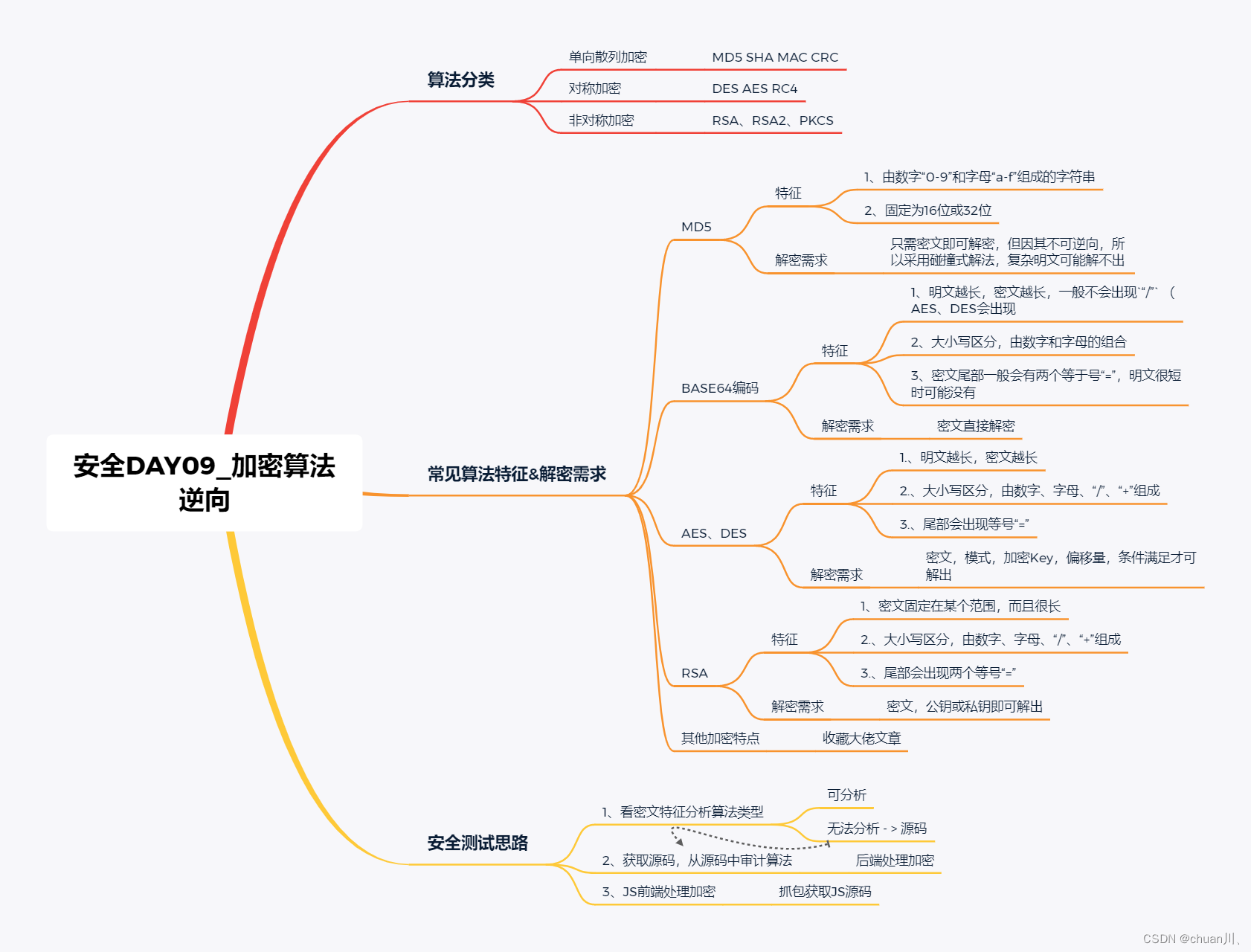
安全学习DAY09_加密逆向,特征识别
算法逆向&加密算法分类,特征识别 文章目录 算法逆向&加密算法分类,特征识别算法概念,分类单向散列加密 - MD5对称加密 - AES非对称加密 - RSA 常见加密算法识别特征,解密特点MD5密文特点BASE64编码特点AES、DES特点RSA密文…...
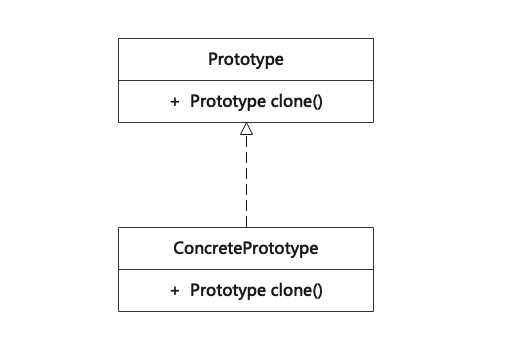
原型模式(Prototype)
原型模式是一种创建型设计模式,使调用方能够复制已有对象,而又无需使代码依赖它们所属的类。当有一个类的实例(原型),并且想通过复制原型来创建新对象时,通常会使用原型模式。 The Prototype pattern is g…...
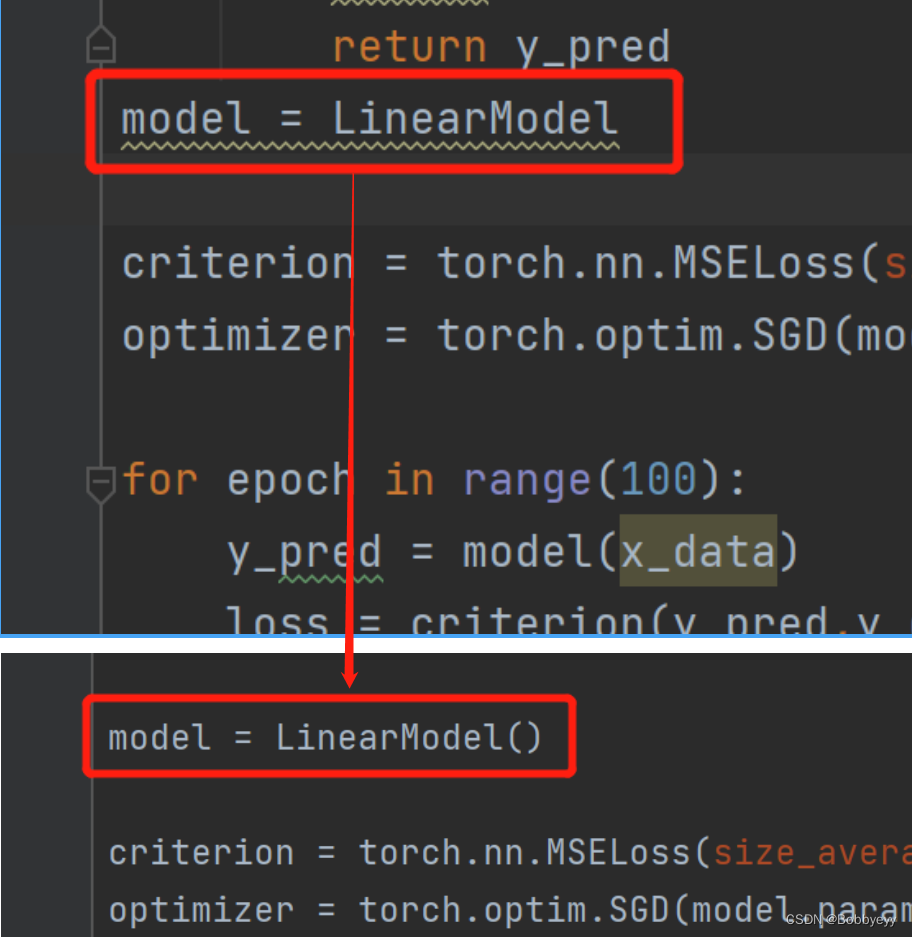
深度学习之用PyTorch实现线性回归
代码 # 调用库 import torch# 数据准备 x_data torch.Tensor([[1.0], [2.0], [3.0]]) # 训练集输入值 y_data torch.Tensor([[2.0], [4.0], [6.0]]) # 训练集输出值# 定义线性回归模型 class LinearModel(torch.nn.Module):def __init__(self):super(LinearModel, self)._…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...
