时间复杂度介绍及其计算
时间复杂度
1.算法效率
如何衡量一个算法的好坏呢?看这段代码:
long long Fib(int N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
这是斐波那契数列的递归代码,非常简洁,那么这就一定说明它好吗?答案显而易见。
2.算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
==时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。==在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
3.算法的时间复杂度
概念:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,就是算法的时间复杂度。
也就是:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
Test01
//计算Func1中的++count语句执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
count++语句的执行次数:F(N) = N^2 + 2N +10
- N=10时:F(N) = 130
- N=100,F(N) = 10210
- n = 1000,F(N) = 1002010
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
大O阶的推导方法:
- 若最高阶项不存在,则用常数1取代运行时间中所有的常数部分。
- 在修改后的运行函数次数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
那么在Test01中,使用大O表示法之后:时间复杂度为 O(N^2)
大O表示法实际上是去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个不重复长度为N的数组中寻找一个值为x的下标。
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
但是在实际操作中,一般关注的是算法的最坏运行情况所以数组中搜索数据时间复杂度为O(N)。
Test02:
//计算Func2中的++count语句执行了多少次?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
Test02的时间复杂度用大O的渐进表示法就为:O(N)。
原因解释:这里的++count语句严格计算的话:共执行了:2N+10次,但是根据大O的渐进表示规则:最高阶项是2N,这里将2去掉,剩下的部分就是时间复杂度。
Test03:
//计算Func3中的++count语句执行了多少次?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}
Test03的时间复杂度为:
- 若N与M接近:则O(N)或者O(M)都可以。(当N与M接近时,++count语句的执行次数接近于2N或2M,再去掉常数部分,即可得到答案)
- 若M>>N,则为O(M)。(当M>>N时,N就可忽略不计。)
- 若N>>M,则为O(N)。
Test04:
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}
Test04的时间复杂度为:O(1)
解释:无论其他变量如何变化,++count语句始终会执行100次,始终为常数次,时间复杂度用大O的渐进表示法则为:O(1)。
Test05:
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character );
strchr函数的功能是:在str字符串中寻找character字符的下标,若不存在则返回-1。这个函数查找的可以分为最好和最坏两种情况:
- 最好情况:1次就找到
- 最坏情况:搜完整个字符串才找到或者不存在。
而在大O的渐进表示法中,一般表示最坏的情况,假设字符串的长度为N,那么strchr函数的时间复杂度就是O(N)了。
Test06:
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
Test06的时间复杂度为:O(N2).
原因:冒泡排序是由两层循环嵌套实现的,数组长度为n。假设最坏情况:数组中的元素由大到小排列。外层循环要执行n-1次,内层循环会随着外层循环的增加而减少,所以整体的执行次数为:(N-1) + (N-2) + (N-3) + (N-4) + ……+1,这是一串等差数列,最高阶项就是N2,所以时间复杂度也就是O(N2)。
Test07:
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}
Test07的时间复杂度是:O(logN),(以2为底,N的对数)。
解释:考虑最差情况:要寻找的数在边界上,即二分区间之内只有一个数。一个长度为N的数组,要执行多少次二分,才能让二分区间只有一个数字?答案是logN次。所以时间复杂度就为O(logN)。
二分查找的效率是非常高的,但是由于被二分的数组必须有序,那么二分查找才能有效执行,这就导致了二分查找是不经常使用的。
注意:logN这种写法,如无特殊说明,底数都是2.
Test08:
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}
Test08的时间复杂度为:O(N)
解释:Fac是一个用于计算阶层的函数,这里的递归次数取决于参数N。递归调用的复杂度就是多次调用次数的累加,而在每一次的递归调用中,语句的执行次数为常数次,也就是O(1),这里的时间复杂度就是函数的调用次数了,也就是O(N)。
Test09:
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
Test09的时间复杂度为:O(N2)
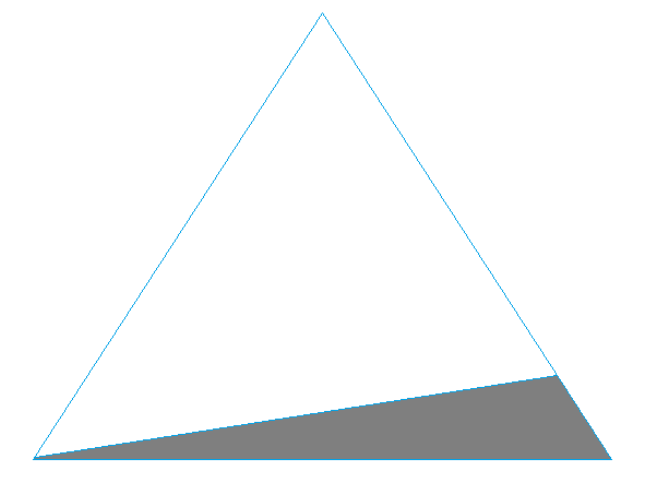
解释:函数每调用一次,就会再次向下调用两次这个函数,直到一方调用到F(2)或F(1)为止。如图所示,如图的每一层,函数调用次数会随着函数调用深度而增加,由20 到 21 ,22,直到2 N-1 ,再对这些调用次数进行相加,再使用大O的渐进表示法,最后就能得到时间复杂度。调用到最后,会形成一个类似等腰三角形的形状。灰色部分是无函数调用,白色部分是函数调用。
![> [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bn2iJWH4-1690516905323)(C:\Users\30539\AppData\Roaming\Typora\typora-user-images\image-20230728115653304.png)]](https://img-blog.csdnimg.cn/6ab3dab006ce4c508387b5c48f3b4236.png)
![> [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cf44B8WL-1690516905324)(C:\Users\30539\AppData\Roaming\Typora\typora-user-images\image-20230728115613047.png)]](https://img-blog.csdnimg.cn/9318217815b1473cb3dd582b80f7d735.png)
4.完结
时间复杂度的内容就到这里啦,若有不足,欢迎评论区指正,下期见!
相关文章:
时间复杂度介绍及其计算
时间复杂度 1.算法效率 如何衡量一个算法的好坏呢?看这段代码: long long Fib(int N) {if(N < 3)return 1;return Fib(N-1) Fib(N-2); }这是斐波那契数列的递归代码,非常简洁,那么这就一定说明它好吗?答案显而易…...
etcd实现大规模服务治理应用实战
导读:服务治理目前越来越被企业建设所重视,特别现在云原生,微服务等各种技术被更多的企业所应用,本文内容是百度小程序团队基于大模型服务治理实战经验的一些总结,同时结合当前较火的分布式开源kv产品etcd,…...

目标检测中 anchor base和anchor free
目标检测中两种不同anchor的生成 趋势:anchor free越来越受到实时性检测的青睐,,,...

TypeC拓展设计方案|TypeC转HDMI设计方案|CS5261/CS5265芯片设计参数对比
集睿智远CS5261/CS5265都可以用于设计TypeC转HDMI方案,低成本TypeC扩展坞设计方案,而两者也有些差异:1.CS5261支持DP1.4输入,一个HDMI1.4输出,即HDMI输出为4K30HZ ;CS5265DP1.4到HDMI2.0转换芯片,即HDMI输出…...
SQL Developer中的Active Data Guard
这篇文章 Display Data Guard configuration in SQL Developer 中,用SQL Developer展示了多种ADG的拓扑。 今天自己也试了一下,还蛮简单的,其实最麻烦的部分在于搭建一个ADG环境。 假设我已有一个ADG环境,即最典型的环境&#x…...

谈谈FFT到底有何用
谈谈FFT到底有何用 FFT快速傅里叶变换是数字信号处理的经典算法,学过DSP或者芯片设计的人大多知道这个算法;但是,大家是否想过,为什么数字信号处理会有那么多FFT呢有人会说,为了分析信号的频谱;那么下边的问题就是,分析频谱对我们的日常需求,比如手机打电话,雷达测量速度和方向…...
MATLAB | 如何绘制这样的描边散点图?
part.-1 前前言 最近略忙可能更新的内容会比较简单,见谅哇,今日更新内容: part.0 前言 看到gzhBYtools科研笔记(推荐大家可以去瞅瞅,有很多有意思的图形的R语言复现!!)做了这样一张图: 感觉很…...

偶数科技与白鲸开源完成兼容性认证
近日,偶数科技自主研发的云原生分布式数据库 OushuDB v5.0 完成了与白鲸开源集成调度工具 WhaleStudio v2.0 的兼容性相互认证测试。 测试结果显示,双方产品相互良好兼容,稳定运行、安全,同时可以满足性能需求,为企业级…...
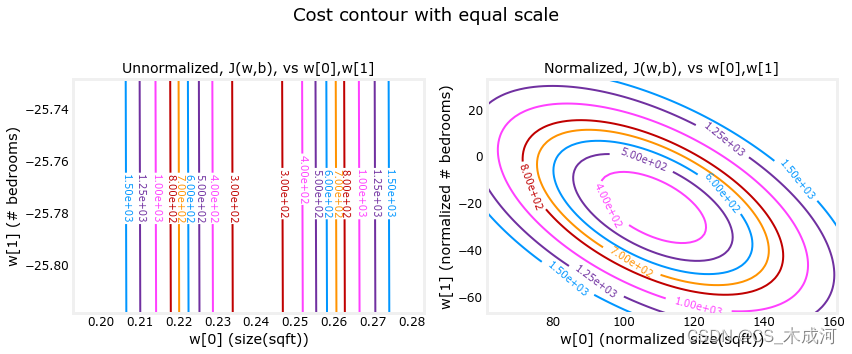
【机器学习】Feature scaling and Learning Rate (Multi-variable)
Feature scaling and Learning Rate 1、数据集2、学习率2.1 α \alpha α 9.9e-72.2 α \alpha α 9e-72.3 α \alpha α 1e-7 3、特征缩放3.1 特征缩放的原因3.2 Z-score 归一化3.3 预测3.4 损失等值线 导入所需的库 import numpy as np np.set_printoptions(precision…...
windows编译ncnn
官方代码https://github.com/Tencent/ncnn/wiki/how-to-build#build-for-windows-x64-using-visual-studio-community-2017 编译工具 visual studio 2017 一、编译protobuf 1、下载protobuf protobuf-3.11.2:https://github.com/google/protobuf/archive/v3.11…...

C++和Lua交互总结
C和Lua交互总结 Chapter1. C和Lua交互总结一、Lua与C的交互机制——Lua堆栈二、堆栈的操作三、C 调用 Lua1)C获取Lua值2)C调用Lua函数示例: 四、Lua 调用 C包装C函数 最后总结一下 Chapter1. C和Lua交互总结 原文链接:https://bl…...

nvm安装和切换node版本
1、nvm list查看已安装的node版本 2、查看当前使用的npm和node版本 3、安装某版本的node 4、 切换node版本...
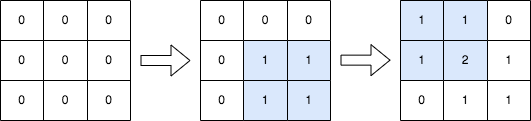
每日一题8.2 2536
2536. 子矩阵元素加 1 给你一个正整数 n ,表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ,矩阵中填满了 0 。 另给你一个二维整数数组 query 。针对每个查询 query[i] [row1i, col1i, row2i, col2i] ,请你执行下述操作:…...
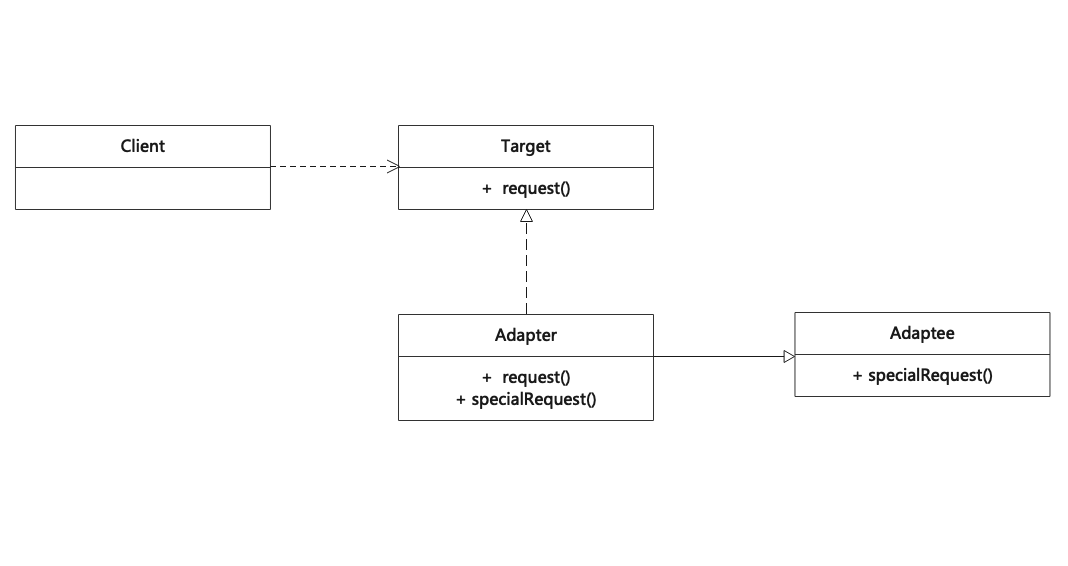
适配器模式(Adapter)
适配器模式用于将一个接口转换成用户希望的另一个接口,适配器模式使接口不兼容的那些类可以一起工作,其别名为包装器(Wrapper)。适配器模式既可以作为类结构型模式,也可以作为对象结构型模式。 Adapter is a structural design pattern that…...

Spring学习笔记——1
Spring学习笔记——1 一、Spring入门1.1、学习路线1.2、传统Javaweb开发困惑及解决方法1.3、三种思想的提出和框架概念1.3.1、IoC、DI和AOP思想提出1.3.2、框架的基本特点 1.4、Spring概述1.5、BeanFactory快速入门1.6、ApplicationContext快速入门1.7、BeanFactory与Applicati…...
leetcode 406. 根据身高重建队列
2023.8.2 这题一开始有点让人懵逼的是有两个维度,一个是身高,还一个是前面人高于自己的人数。这种题一般需要先固定一个维度,再去确定另外一个维度,不要想着兼顾。 经过纸上模拟,我的思路是先通过身高进行从大到小排序…...

Matlab实现AGNES算法
在数据分析和机器学习中,聚类是一种常用的无监督学习方法,它可以将数据点按照某种相似度标准进行分组,从而发现数据中的结构和模式。聚类算法有很多种,其中一种比较经典的是AGNES算法,它是一种基于层次的聚类算法&…...
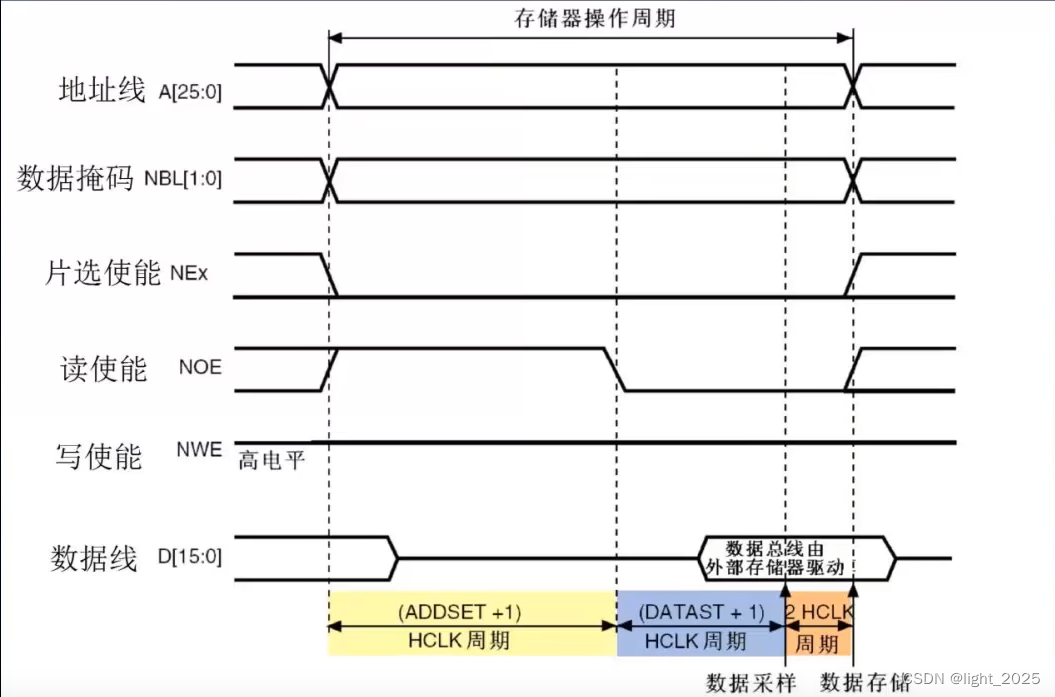
STM32F4_外部SRAM
目录 前言 1. SRAM控制原理 1.1 SRAM功能框图 1.2 SRAM读写时序 2. FSMC简介 2.1 FSMC架构 2.2 FSMC地址映射 2.3 FSMC控制SRAM时序 3. FSMC结构体 4. 库函数配置FSMC 5. 实验程序 5.1 main.c 5.2 SRAM.c 5.3 SRAM.h 前言 STM32F4自带了192K字节的SRAM࿱…...
Java的代理模式
java有三种代理模式 静态代理 jdk动态代理 cglib实现动态代理 代理模式的定义: 为其他对象提供一种代理以控制对这个对象的访问。在某些情况下,一个对象不适合或者不能直接引用另一个对象,而代理对象可以在客户端和目标对象之间起到中介的…...

FilterAttributeOnClassMethod
目录 1 BadMethodFilterAttribute 2 FilterAttributeOnClassMethod 2.1 OnMethodExecuted 2.2 OnMethodExecutedAsync 2.3 OnMethodExecuting BadMethodFilterAttribute using System; using System.Threading.Tasks; namespace Flatwhite.Core.Tests.Attributes …...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

【java】【服务器】线程上下文丢失 是指什么
目录 ■前言 ■正文开始 线程上下文的核心组成部分 为什么会出现上下文丢失? 直观示例说明 为什么上下文如此重要? 解决上下文丢失的关键 总结 ■如果我想在servlet中使用线程,代码应该如何实现 推荐方案:使用 ManagedE…...
