算法题--二叉树(二叉树的最近公共祖先、重建二叉树、二叉搜索树的后序遍历序列)
目录
二叉树
题目
二叉树的最近公共祖先
原题链接
解析
二叉搜索树的最近公共节点
核心思想
答案
重建二叉树
题目链接
解析
核心思想
答案
二叉搜索树的后序遍历序列
原题链接
解析
核心思想
答案
二叉树
该类题目的解决一般是通过节点的遍历去实现,一般是分两种。
一是递归(深度优先),该方法通常代码比较简单,难懂。首先需要确定入参和返回的内容,然后确定层级之间的关系,最后去找递归的出口。
二是广度优先(该方法一般只有可以分层次处理的才能用),该方法代码量多,易懂。首先借助数组存储第一层的节点,然后每次将数组中的节点分批从数组头部取出(当对比2个节点时就一次取2个),处理完后将对应的子节点分批再从数组尾部存入数组(注意需要对比的子节点相邻存入,这样取出正好配对)。递归上述步骤直到数组为空。
注意特殊的二叉树会满足一些条件。
题目
二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
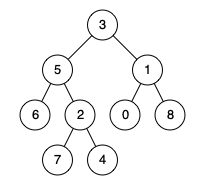
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点5和节点1的最近公共祖先是节点3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点5和节点4的最近公共祖先是节点5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
/*** Definition for a binary tree node.* function TreeNode(val) {* this.val = val;* this.left = this.right = null;* }*/
var lowestCommonAncestor = function(root, p, q) {};原题链接
力扣
解析
注意一些树的节点之间会有大小关系,更方便于解题,例如二叉搜索树,二叉搜索树的左节点(包括其子节点上的值)小于根节点,右节点(包括其子节点上的值)大于根节点。
例如类似题目
二叉搜索树的最近公共节点
力扣
核心思想
方法一(递归)
1.确定入参和出参,入参:1需要检索当前节点root,2需要检索当前的节点下是否有目标节点p、q;出参:返回的目标节点或最近公共节点。
2.确定上下层关系,当root的左右两边节点出现p和q时,当前节点为公共的父节点。当只有一个左右节点中只有一个节点为目标节点时,返回目标节点。
3.找出口,当root不存在、或者root为目标节点时,返回root。
方法二(广度优先+哈希表存储父节点):
1.首先用广度优先算法遍历每个接地那,构建一个哈希表存储子节点对应父节点的关系。
2.求出p的所有父节点放入集合中。
3.从q节点往上取所有父节点,直到有父节点在p的父节点集合中存在。
答案
方法一(递归)
var lowestCommonAncestor = function (root, p, q) {if (!root || root === p || root === q) return root;const left = lowestCommonAncestor(root.left, p, q);const right = lowestCommonAncestor(root.right, p, q);if(left && right){return root}else{return left||right}
};方法二(广度优先+哈希表存储父节点)
var lowestCommonAncestor = function(root, p, q) {let queue = [root],parent = new Map();while(queue.length && (!parent.has(p) || !parent.has(q))){const node = queue.shift();node.left && queue.push(node.left);node.right && queue.push(node.right);node.left && parent.set(node.left, node);node.right && parent.set(node.right,node);}let pSet = new Set(),node = p;pSet.add(node);while(parent.has(node)){pSet.add(parent.get(node));node = parent.get(node);}node = q;if(pSet.has(node)) return node;while(parent.has(node)){node = parent.get(node);if(pSet.has(node)) return node;}return null;
};重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1] Output: [-1]
/*** Definition for a binary tree node.* function TreeNode(val) {* this.val = val;* this.left = this.right = null;* }*/
var buildTree = function(preorder, inorder) {};题目链接
力扣
解析
前序遍历的顺序是根左右,中序遍历的顺序为左根右。
以示例1解释,[3,9,20,15,7]前序遍历的第一个值3一定为根的值,我们将它取出,前序遍历剩余[9,20,15,7]。
3在中序遍历[9,3,15,20,7]中的位置,可以分割出[9],[15,20,7],我们知道[9]一定是根3的左子树的中序遍历,[15,20,7]一定是根3的右子树的中序遍历。
核心思想
递归
1.确定入参和出参,入参:前序遍历的后续遍历的序列。出参:根据遍历返回的当前根节点。
2.确定上下层关系,每次根据前序找到根节点,根据根节点在中序中划分属于左右节点的部分。
f(p,q)={ val:xxx,left:f(pl,ql),right:f(pr,qr)}。
3.找出口,当preorder不存在时。
答案
递归
var buildTree = function(preorder, inorder) {if (!preorder.length) {return;}const val = preorder.shift()const index = inorder.findIndex(item => item === val)const left = inorder.slice(0, index)const right = inorder.slice(index + 1)return {val,left: buildTree(preorder.slice(0, index), left),right: buildTree(preorder.slice(index), right)}
};
二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5/ \2 6/ \1 3
示例 1:
输入: [1,6,3,2,5] 输出: false
示例 2:
输入: [1,3,2,6,5] 输出: true
/*** @param {number[]} postorder* @return {boolean}*/
var verifyPostorder = function(postorder) {};原题链接
力扣
解析
二叉搜索树的左节点(包括其子节点上的值)小于根节点,右节点(包括其子节点上的值)大于根节点。故二叉搜索树可以只根据一个顺序的序列结果就可以构造树。
核心思想
递归
1.确定入参和出参,入参:当前序列。
2.确定上下层关系,取序列最后一个节点为根节点,每次根据当前序列,找到第一个大于根节点的,该元素的左边应该全部小于根节点,右边应该全部大于根节点,满足的话对左右两边的序列进行递归,f(x)=f(x.left)&&f(x.right)。
3.找出口,当preorder不存在时结束。
答案
递归
var verifyPostorder = function(postorder) {if (postorder.length <= 2) {return true}const root = postorder.pop()let index = postorder.findIndex(num => num > root)index = index === -1 ? postorder.length : indexconst left = postorder.slice(0, index)const right = postorder.slice(index)if(!(left.every(num => num < root) && right.every(num => num > root))){return false}return verifyPostorder(left) && verifyPostorder(right)
};相关文章:

算法题--二叉树(二叉树的最近公共祖先、重建二叉树、二叉搜索树的后序遍历序列)
目录 二叉树 题目 二叉树的最近公共祖先 原题链接 解析 二叉搜索树的最近公共节点 核心思想 答案 重建二叉树 题目链接 解析 核心思想 答案 二叉搜索树的后序遍历序列 原题链接 解析 核心思想 答案 二叉树 该类题目的解决一般是通过节点的遍历去实现&#x…...

mysql的基础面经-索引、事务
1 聚簇索引 1 和主键索引的关系 2 和非聚簇索引的关系,其叶子节点存储的是聚簇索引中的主键 3 索引覆盖机制使得非聚簇索引不用回表二次查询 2 举一个使用索引覆盖的例子 我的项目中没有使用到覆盖索引,但是可以举一个例子,比如我直接为年…...

Windows下双网卡配置静态路由,实现内外网同时使用
怎么样设置双网卡?内网外网两个网络这么同时连接? 接下来听好了,赶紧动手 情况描述: 我使用的Windows10电脑,支持双网卡工作 目前我工作需要使用的使用内网,但是又需要使用外网,需要同时使用&a…...

Spring整合Mybatis、Spring整合JUnit
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaweb 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 Spring整合 一、Spring整合Mybatis1.1 整合Mybatis&#x…...
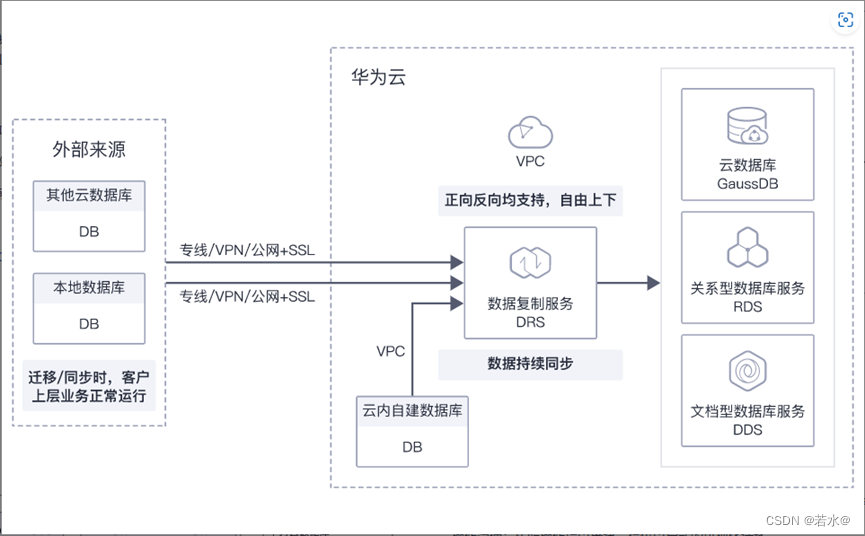
Devops系统中jira平台迁移
需求:把aws中的devops系统迁移到华为云中,其中主要是jira系统中的数据迁移,主要方法为在华为云中建立一套 与aws相同的devops平台,再把数据库和文件系统中的数据迁移,最后进行测试。 主要涉及到的服务集群CCE、数据库mysql、弹性文件服务SFS、数据复制DRS、弹性负载均衡ELB。 迁…...

【雕爷学编程】MicroPython动手做(29)——物联网之SIoT
知识点:什么是掌控板? 掌控板是一块普及STEAM创客教育、人工智能教育、机器人编程教育的开源智能硬件。它集成ESP-32高性能双核芯片,支持WiFi和蓝牙双模通信,可作为物联网节点,实现物联网应用。同时掌控板上集成了OLED…...
LAXCUS分布式操作系统引领科技潮流,进入百度首页
信息源自某家网络平台,以下原样摘抄贴出。 随着科技的飞速发展,分布式操作系统做为通用基础平台,为大数据、高性能计算、人工智能提供了强大的数据和算力支持,已经成为了当今计算机领域的研究热点。近日,一款名为LAXCU…...

Linux--按行读取数据:fgets
函数定义: char *fgets(char *s,int size,FILE *stream); S是指接受数据缓冲区,用于存放stream里读取的数据 size是指缓冲区的大小 返回值为NULL表明读取失败,反之读取成功...

express学习笔记5 - 自定义路由异常处理中间件
修改router/index.js,添加异常处理中间件 *** 自定义路由异常处理中间件* 注意两点:* 第一,方法的参数不能减少* 第二,方法的必须放在路由最后*/ router.use((err, req, res, next) > {console.log(err);const msg (err &…...
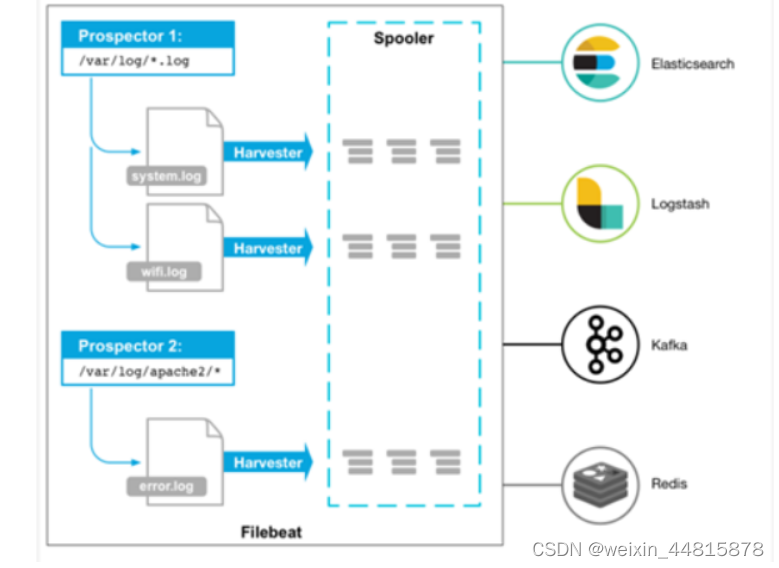
filebeat介绍
1、filebeat概述 Filebeat是用于转发和集中日志数据的轻量级传送工具。Filebeat监视您指定的日志文件或位置,收集日志事件,并将它们转发到Elasticsearch或 Logstash或kafka进行索引 1.1 Filebeat两个主要组件 prospector 和 harvester。 prospector&a…...
使用SSM框架实现个人博客管理平台以及实现Web自动化测试
文章目录 前言1. 项目概述2. 项目需求2.1功能需求2.2 其他需求2.3 系统功能模块图 3. 开发环境4. 项目结构5. 部分功能介绍5.1 数据库密码密文存储5.2 统一数据格式返回5.3 登录拦截器 6. 项目展示7. 项目测试7.1 测试用例7.2 执行部分自动化测试用例 前言 在几个月前实现了一…...

【深度学习】MAT: Mask-Aware Transformer for Large Hole Image Inpainting
论文:https://arxiv.org/abs/2203.15270 代码:https://github.com/fenglinglwb/MAT 文章目录 AbstractIntroductionRelated WorkMethod总体架构卷积头Transformer主体Adjusted Transformer Block Multi-Head Contextual Attention Style Manipulation Mo…...

PyTorch BatchNorm2d详解
通常和卷积层,激活函数一起使用...
慕课网Go-4.package、单元测试、并发编程
package 1_1_User.go package usertype User struct {Name string }1_1_UserGet.go package userfunc GetCourse(c User) string {return c.Name }1_1_UserMain.go package mainimport ("fmt"Userch03 "goproj/IMOOC/ch03/user"//别名,防止同名…...

[JavaWeb]SQL介绍-DDL-DML
SQL介绍-DDL-DML 一.SQL简介1.简介2.SQL通用语法3.SQL语言的分类 二.DDL-操作数据库与表1.DDL操作数据库2.DDL操作表①.查询表(Retrieve)②.创建表(Create)③.修改表(Update)④.删除表(Delete) 三.Navicat的安装与使用四.DML-操作表数据1.添加(Insert)2.修改(Update)3.删除(Del…...
)
git源码安装(无sudo权限)
git源码安装(无sudo权限) 下载源码解压安装添加到环境变量 下载源码 去https://mirrors.edge.kernel.org/pub/software/scm/git/下载需要的版本。我下载的是2.41.0版本 wget https://mirrors.edge.kernel.org/pub/software/scm/git/git-2.41.0.tar.gz解…...
Web3 叙述交易所授权置换概念 编写transferFrom与approve函数
前文 Web3带着大家根据ERC-20文档编写自己的第一个代币solidity智能合约 中 我们通过ERC-20一种开发者设计的不成文规定 也将我们的代币开发的很像个样子了 我们打开 ERC-20文档 我们transfer后面的函数就是transferFrom 这个也是 一个账号 from 发送给另一个账号 to 数量 val…...
Redis系列二:Clion+MAC+Redis环境搭建
1. ClionMACRedis-3.0-annotated环境搭建 参考: https://github.com/huangz1990/redis-3.0-annotated https://gitee.com/dumpcao/redis-3.0-annotated-cmake-in-clion https://tool.4xseo.com/a/12910.html 1.1 下载并导入Clion git clone https://gitee.com/dum…...
Linux下 Docker容器引擎基础(2)
目录 创建私有仓库 将修改过的nginx镜像做标记封装,准备上传到私有仓库 将镜像上传到私有仓库 从私有仓库中下载镜像到本地 CPU使用率 CPU共享比例 CPU周期限制 CPU 配额控制参数的混合案例 内存限制 Block IO 的限制 限制bps 和iops 创建私有仓库 仓库&a…...

现场服务管理系统有哪些?5个现场服务管理软件对比
现场售后服务管理软件的使用者通常是机械设备、家电、仪表仪器、医疗器械等厂商的工程师和客服调度人员。现场售后服务管理软件可将服务过程标准化,包括工单派发、服务过程步骤、配件订购出货和付款、客户评价都有系统支持,有的现场售后服务软件还支持数…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...
