【数据结构与算法分析】介绍蛮力法以及相关程序案例
文章目录
- 蛮力法之排序
- 选择排序
- 冒泡排序
- 实际应用
- 蛮力法之最近对和凸包问题
- 最近对问题
- 凸包问题
蛮力法(brute force),其本质跟咱常说的暴力法是一样的,都是一种简单直接地解决问题的方法,通常直接基于问题的描述和所涉及的概念定义进行求解。
蛮力法之排序
选择排序
选择排序,其本质是将位置与对应的数据大小相匹配,比如:在遍历整个列表时,先找到最小(大)的元素,将其与第一个元素交换;再从第二个元素开始遍历,找到第二小(大)的元素,将其与第二个元素交换;再从第n-1个元素开始遍历,找到第n-1小(大)的元素,将其与第n-1个元素交换。在遍历列表n-1次后,列表就按指定顺序排列完成。此时:
A1⩽A2⩽A3⩽……⩽An−1⩽AnA~1~\leqslant A~2~\leqslant A~3~\leqslant ……\leqslant A~n-1~\leqslant An A 1 ⩽A 2 ⩽A 3 ⩽……⩽A n−1 ⩽An
其实现代码为:
void selectSort(int*a,int len)
{for(int i=0;i<len;++i){for(int j=i+1;j<len;++j){if(a[i]>a[j]){int temp = a[i];a[i] = a[j];a[j] = temp;}}}
}
案例分析
如果我们使用选择排序对列表 0,2,4,1,9,6,3,8,5,7进行排序,那么其排序过程将会是:

使用DEV跑得到结果:

其时间复杂度为O(n2),空间复杂度为0(n)
)
冒泡排序
冒泡排序,其本质是比较相邻两个元素大小,即,如果 an-1< an ,那么就交换两者位置, 而选择排序是选择相应的元素放置到合适的位置。
其实现代码为:
void bubbleSort(int*a,int len)
{for(int i=0;i<len-1;++i){for(int j=0;j<len-1-i;++j){if(a[j]>a[j+1]){int temp = a[j+1];a[j+1] = a[j];a[j] = temp;}}}
}
案例分析
如果我们使用冒泡排序对列表 0,2,4,1,9,6,3,8,5,7进行排序,那么其排序过程将会是:

使用DEV跑得到结果:

与选择排序一样,其时间复杂度为O(n2),空间复杂度为0(n)
实际应用
问题:应用选择排序将序列E,X,A, M,P,L,E按照字母顺序排序。
程序解答
直接将上述的选择排序排序内容从整数变成字符即可,一样的逻辑。
#include <iostream>
using namespace std;void outPut(char *a,int len)
{for(int i=0;i<len;i++)cout<<a[i]<<" ";cout<<endl;
}void selectSort(char*a,int len)
{for(int i=0;i<len-1;++i){for(int j=i+1;j<len;++j){if(a[i]>a[j]){char temp = a[i];a[i] = a[j];a[j] = temp;}}}
}int main(void)
{char a[] = {'E','X','A','M','P','L','E'};cout<<"排序前:";outPut(a,7);selectSort(a,7);cout<<"排序后:";outPut(a,7);return 0;
}
蛮力法之最近对和凸包问题
最近对问题
最近对问题描述
最近点对问题要求:在一个包含n个点的集合中,找出距离最近的两个点。这种处理平面或者高维空间的邻近点的问题,在各种计算几何问题当中是最简单的。问题中的点可以代表飞机、邮局这类实体对象,也可以代表数据库记录、统计样本或者 DNA序列等非实体对象。航空交通控制人员可能会对两架最可能发生碰撞的飞机感兴趣。区域邮政管理者可能需要依赖最近对问题的解来寻找地理位置最近的邮局。
解答
使用蛮力法解决最近对问题,一般是采用先将任意两点之间的距离求出,再找到这些距离中的最小值。
例如:
题目
在集合{16,4,23,6,5,94,77}中打印出两数差值最小的两个数;
解析:
由上述最近对问题核心:求两两数值的最小差值,不难有下图中的求解过程:

根据上述的模拟过程,可写出下述程序:
#include <iostream>
#include <math.h>
using namespace std;void findMinValue(int*a,int len)
{int minValue,dp[2];// 遍历数组 求任意两数之差 for(int i=0;i<len-1;i++){for(int j=i+1;j<len;j++){int temp = abs(a[i]-a[j]);// 比较是否是最小的差 if((i==0&&j==1) || temp < minValue){dp[0] = a[i];dp[1] = a[j];minValue = temp;}} } cout<<"差值最小的两数为:"<<dp[0]<<" "<<dp[1]<<endl;
} int main(void)
{int a[] = {16,4,23,61,5,94,77};findMinValue(a,7);return 0;
}
使用DEV运行求解有:
与选择排序类似,该程序的时间复杂度为O(n2),空间复杂度为O(n)。
凸包问题
设p,=(x1, y1), p2=(x2,y2). …, pn=(xn,yn)是平面上n个点构成的集合S,包含集合S中所有点的最小多边形就称为凸包多边形,也就是将最外围所有点连接起来构成的多变形,将其称为凸包多边形。 下图就是一个包含点集的凸包多边形。

例如:
求出二维平面中点 (1,1),(2,1)、(4,1)、(2,2)、(3,2)、(4,2)、(2,3)、(4,3)、(5,3)、(3,4) 所构成的最小凸包。
人为画出凸包多边形有:

分析:
凸包多边形,是由点集最外层点所构成,再结合上图,是不是可以看出当凸边多边形边确定时,其他点都在边的一侧。从数学角度上来说,也就是当凸边多边形边确定时,任意一点到这条边的距离的符号相同(即同为正数,或同为负数,或者为0)。
然后,在将任意两点连接构成一条直线,再判断这条直线是否符合上述凸边多边形边的性质,如果符合该性质就这两点加入到结果集中;否则就继续找其他的直线。
当以点(1,1)为凸包多边形边的一点时,将该点依次连接其他任意点,例如:连接点(2,1),通过点到直线的距离公式,可以算出任意点到该直线都为正数,因此,可以作为凸多边形的一边;而连接点(5,3)时,由于点散落在直线两侧,使用距离公式,可以算出部分点到直线距离为正数,而剩余点到直线的距离为负数,因此,该边不可作为凸多边形的一边。

根据上述的分析,可以写出下述程序:
#include<iostream>
#include<cmath>
#include<vector>
#include<map>
using namespace std;int check(vector<pair<float, float> >&data,pair<float, float>&target)
{// 判断数组data中是否已经包含该数值 包含就返回1 否则返回0 for(int i=0;i<data.size();i++)if(data[i].first==target.first && data[i].second==target.second)return 1;return 0;
}vector<pair<float, float> > convexHull(vector<pair<float,float> > &point){// 集合点少于2时 可以直接返回 if(point.size() <= 2) return point;vector<pair<float, float> > pointPairVec;//两个循环扫描每个点for(int i=0; i<point.size()-1; i++){for(int j=i+1; j<point.size(); j++){// 求一个一次函数的直线A:ax+by=c (a=y2-y1,b=x2-x1,c=x1y2-y1x2)float a = point[j].second - point[i].second; float b = point[i].first - point[j].first;float c = point[i].first*point[j].second - point[i].second*point[j].first;//记录直线两边的点int sign1 = 0, sign2 = 0; //扫描直线A外的所有的点for(int k=0; k<point.size(); k++){if(k==i || k==j)continue;else{// 求点到直线A的距离 float sign = a*point[k].first + b*point[k].second - c;// 该点在直线上边 if(sign > 0)sign1++;// 该点在直线下边else if(sign < 0)sign2++; } }// 该点不符合要求 继续查找 if(sign1 > 0 && sign2 > 0)continue;// 将符合要求的两点加入结果集 else{// 将不重复的值加入到结果集 if(!check(pointPairVec,point[i]))pointPairVec.push_back(point[i]);if(!check(pointPairVec,point[j])) pointPairVec.push_back(point[j]);} }}return pointPairVec;
}int main(){// 保存数据集vector<pair<float, float> > pointsArray(10);// 生成数据集 pointsArray[0] = pair<float, float>(1,1); pointsArray[1] = pair<float, float>(2,1);pointsArray[2] = pair<float, float>(4,1);pointsArray[3] = pair<float, float>(2,2);pointsArray[4] = pair<float, float>(3,2);pointsArray[5] = pair<float, float>(4,2);pointsArray[6] = pair<float, float>(4,3);pointsArray[7] = pair<float, float>(2,3);pointsArray[8] = pair<float, float>(5,3);pointsArray[9] = pair<float, float>(3,4);cout<<"源数据:"<<endl; for(int i=0; i<pointsArray.size(); i++)cout<<"("<<pointsArray[i].first<<","<<pointsArray[i].second<<")"<<" ";vector<pair<float, float> > convex = convexHull(pointsArray);cout<<endl<<"求出能够构成凸包的点:"<<endl;for(int i=0; i<convex.size(); i++)cout<<"("<<convex[i].first<<","<<convex[i].second<<")"<<" ";return 0;
}
DEV跑出结果为:

小编主学嵌入式,算法能力一般,欢迎大家查看小编其他文章,同时也欢迎大家留言或私信交流哈!
相关文章:

【数据结构与算法分析】介绍蛮力法以及相关程序案例
文章目录蛮力法之排序选择排序冒泡排序实际应用蛮力法之最近对和凸包问题最近对问题凸包问题蛮力法(brute force),其本质跟咱常说的暴力法是一样的,都是一种简单直接地解决问题的方法,通常直接基于问题的描述和所涉及的概念定义进行求解。 蛮…...

用股票交易量查询接口是怎么查询a股全天总成交量的?
用股票交易量查询接口是怎么查询a股全天总成交量的?今天下班就以通达信给大家讲解一下,通常是在K线图的底部状态栏,可以在日线进行查看a股成交量。在市场栏底部的子图中。 有当天成交的数量。成交量是表示一定的时间内已经成交的中的成交数量…...

求职季哪种 Python 程序员能拿高薪?
本文以Python爬虫、数据分析、后端、数据挖掘、全栈开发、运维开发、高级开发工程师、大数据、机器学习、架构师这10个岗位,从拉勾网上爬取了相应的职位信息和任职要求,并通过数据分析可视化,直观地展示了这10个职位的平均薪资和学历、工作经…...

如何选择好的IB课程学校?
在上海除了拼中考,你还可以走一条更有“选择权”的路——国际化学校! 然而选择学校时,让家长最头痛的事情,莫过于为孩子选择什么样的国际化课程。 今天我们来聊聊IB课程! 三大主流国际课程中,被公认含金量最…...

2023美赛ABCDEF题思路+参考文献+代码
选题建议、ABCDEF题参考文献、ABCDEF题思路(后续更新视频和代码)、D题数据、数据集及处理方式已更新,其他日内更新。下文包含:2023年美国大学生数学建模竞赛(以下简称美赛)A - F题思路解析、选题建议、代码…...
DataEase 制作数据可视化大屏经验分享
前言 DataEase 简介 DataEase 是开源的数据可视化分析工具,帮助用户快速分析数据并洞察业务趋势,从而实现业务的改进与优化。DataEase 支持丰富的数据源连接,能够通过拖拉拽方式快速制作图表,并可以方便地与他人分享。 更多详细介…...

前端基础-2day
前端基础 这里写目录标题前端基础div和span标签div 标签span标签列表有序列表无序列表自定义列表图片超链接标签表格 table表格合并表单标签表单控键属性div和span标签 div 标签 没有具体的含义,用于划分页面区域,独占一行 快捷键:div{}*3 …...

在线一键JS混淆还原
当今,随着互联网的发展,越来越多的网站开始使用JavaScript来实现动态交互和用户体验。但是,由于JavaScript代码的开放性和易于复制,网站管理员需要采取一些措施来保护他们的代码。这就是JavaScript混淆工具产生的原因。 jsjiami.…...

Java基本语法
目录 一、注释方式 1、单行注释 // 2、多行注释 /*...*/ 3、文档注释 /**....*/ 二、标识符和关键字 三、数据类型 拓展及面试题讲解 1、整数拓展 进制 二进制0b 八进制0 十六进制0x 2、字符拓展 编码Unicode表 2字节 0~65536 3、字符串拓展 4、布尔值拓展 一、注释方式…...

什么表单设计工具能快速提升办公效率?
在信息化快速发展的年代,谁能掌握更先进的技术,谁就能拥有更广阔的发展前景。在以前的办公环境中,传统的表单制作工具占据了主流地位,随着办公自动化的快速发展,传统表单工具的弊端也暴露出来了,采用更先进…...
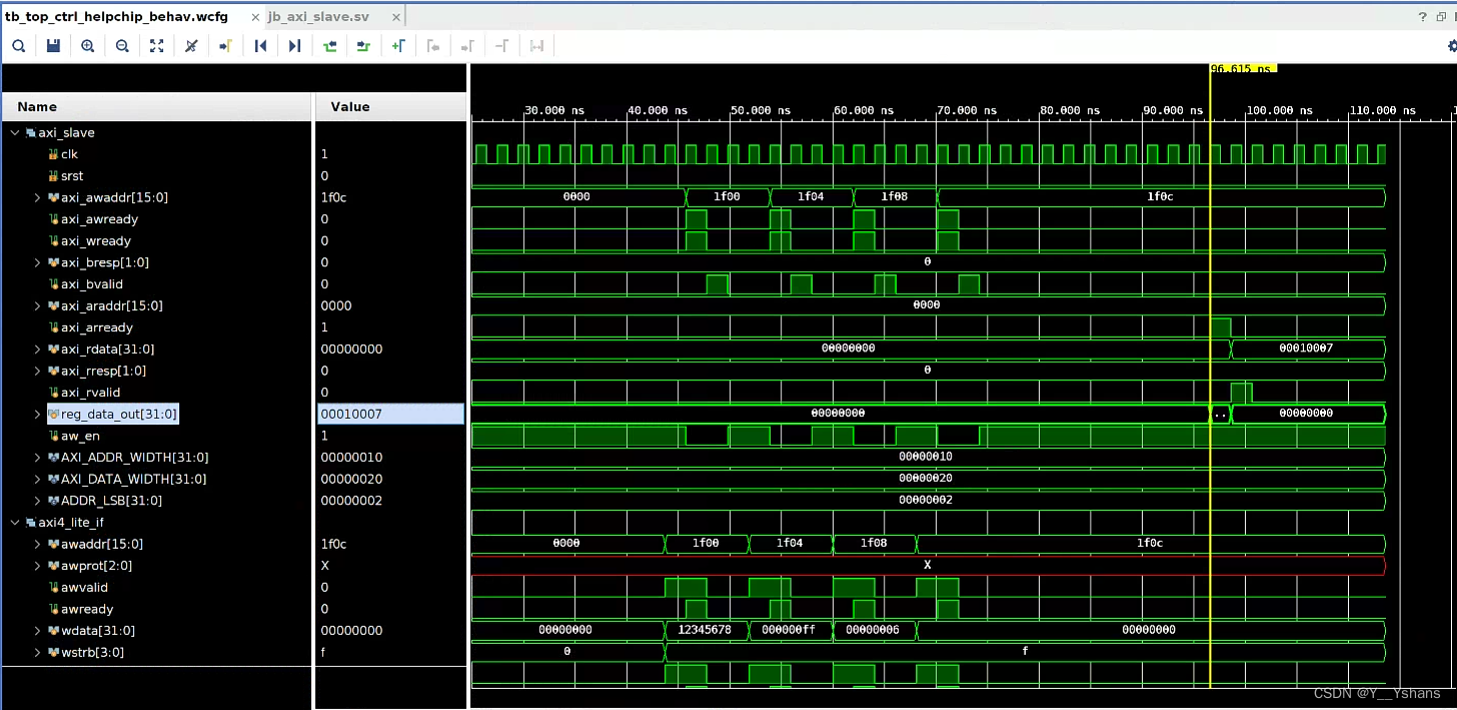
SystemVerilog——Axi4Lite_To_Localbus
摘要:用SystemVerilog对Axi4转localbus进行编写与仿真 如果需要从PS端对PL进行寄存器的读写操作,从znyq M_AXI_HPM_FPD出来,经过axi_interconnect 模块分出多个通道(不同的地址),经过一个axi_slave模块&am…...

硬件_IMX6ULL的LCD控制器
硬件_IMX6ULL的LCD控制器 文章目录硬件_IMX6ULL的LCD控制器一、 LCD控制器模块介绍1.1 硬件框图1.2 数据传输与处理1.3 时序控制二、 LCD控制器寄存器简介2.1 LCDIF_CTRL寄存器2.2 LCDIF_CTRL1寄存器2.3 LCDIF_TRANSFER_COUNT寄存器2.4 LCDIF_VDCTRL0寄存器2.5 LCDIF_VDCTRL1寄…...

ICLR 2022—你不应该错过的 10 篇论文(下)
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 ICLR 2023已经放榜,但是今天我们先来回顾一下去年的ICLR 2022! ICLR 2022将于2022年 4 月 25 日星期一至 4 月 29 日星期五在线举行(连续第三年!&#x…...

国内外优秀程序员的私域博客大全
文章目录 国内外优秀程序员的私域博客大全**国内的优秀程序员****国外的优秀程序员**结语国内外优秀程序员的私域博客大全 国内的优秀程序员 1、风雪之隅-惠新宸 擅长领域:PHP、PECL等 Laruance惠新宸——国内最有影响力的PHP技术专家,PHP开发组核心成员, Zend顾问, PHP7及…...

【C++ Primer Plus】第六章:分支语句和逻辑运算符
文章目录第六章 分支语句和逻辑运算符6.1 字符函数库cctype6.2 ?:运算符6.3 读取数字的输入6.4 cin的处理过程char类型intdoublechar数组使用char数组来存储输入6.5 写入到文本文件中6.6 读取文本文件6.7 总结第六章 分支语句和逻辑运算符 6.1 字符函数库cctype C从C语言继承…...

堡垒机的主要功能是什么?为什么需要堡垒机?
堡垒机是一种用于管理和控制服务器的工具,其主要功能是为管理人员提供安全、便捷的远程管理和操作方式。为什么需要堡垒机呢?下面我们将详细阐述堡垒机的主要功能和必要性。 一、堡垒机的主要功能: ①、用户认证和授权管理:堡垒机…...

记录spring中Transactional事务注解失效的六个场景
记录spring中Transactional事务注解失效的六个场景 方法内的自调用 原因:通过this内部调用其他带有Transactional注解的方法,是通过this进行调用,并没有通过cglib代理对象进行调用,导致方法未被增强导致无法检测内部事务 解决方…...

【23种设计模式】行为型模式详细介绍(下)
前言 本文为 【23种设计模式】行为型模式 相关内容介绍,下边将对访问者模式,模板模式,策略模式,状态模式,观察者模式,备忘录模式,中介者模式,迭代器模式,解释器模式&…...
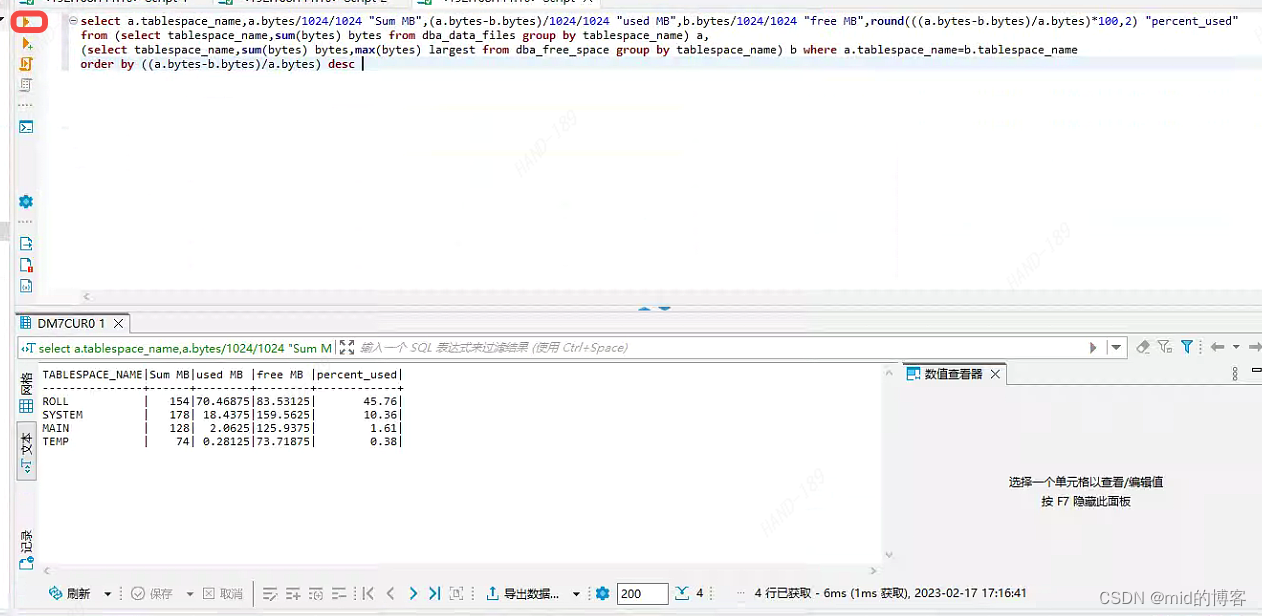
dbeaver工具连接达梦数据库
、一 概述 DBeaver 是一个基于 Java 开发,免费开源的通用数据库管理和开发,DBeaver 采用 Eclipse 框架开发,支持插件扩展,并且提供了许多数据库管理工具:ER 图、数据导入/导出、数据库比较、模拟数据生成等࿰…...
比Teambition、Worktile 更适合研发团队的几大工具盘点
Worktile 和 Teambitiom 哪个更好?两个产品各有特点。1.Teambition 优势:操作简单、个人版永不收费、更适合小型团队;2.Teambition 劣势:无法满足中大型团队复杂的项目管理、自定义能力弱、无法与钉钉以外的工具打通等;…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...

在MobaXterm 打开图形工具firefox
目录 1.安装 X 服务器软件 2.服务器端配置 3.客户端配置 4.安装并打开 Firefox 1.安装 X 服务器软件 Centos系统 # CentOS/RHEL 7 及之前(YUM) sudo yum install xorg-x11-server-Xorg xorg-x11-xinit xorg-x11-utils mesa-libEGL mesa-libGL mesa-…...
