蓝桥杯上岸每日N题 第六期(求阶乘)!!!
蓝桥杯上岸每日N题第六期 ❗️ ❗️ ❗️
同步收录 👇
蓝桥杯上岸必背!!!(持续更新中~)
大家好 我是寸铁💪
冲刺蓝桥杯省一模板大全来啦 🔥
蓝桥杯4月8号就要开始了 🙏
距离蓝桥杯省赛倒数第3天 ❗️ ❗️ ❗️
还没背熟模板的伙伴们背起来 💪 💪 💪
真题千千万万遍,蓝桥省一自然现! ✌️
日更3000里,蓝桥眷顾你 🌟
暴力出奇迹,打表过样例 👊
祝大家4月8号蓝桥杯上岸 ☀️
不清楚蓝桥杯考什么的点点下方👇
考点秘籍
想背纯享模版的伙伴们点点下方👇
蓝桥杯省一你一定不能错过的模板大全(第一期)
蓝桥杯省一你一定不能错过的模板大全(第二期)
蓝桥杯省一你一定不能错过的模板大全(第三期)
蓝桥杯省一你一定不能错过的模板大全(第四期)!!!
想背注释模版的伙伴们点点下方👇
蓝桥杯必背第一期
蓝桥杯必背第二期
往期精彩回顾
蓝桥杯上岸每日N题 第一期(一)!!!
蓝桥杯上岸每日N题第一期(二)!!!
蓝桥杯上岸每日N题第一期(三)!!!
蓝桥杯上岸每日N题第二期(一)!!!
蓝桥杯上岸每日N题第三期(一)!!!
蓝桥杯上岸每日N题 第四期(最少刷题数)!!!
蓝桥杯上岸每日N题 第五期(山)!!!
操作系统期末题库 第九期(完结)
LeetCode Hot100 刷题(第三期)
idea创建SpringBoot项目报错解决方案
数据库SQL语句(期末冲刺)
想看JavaB组填空题的伙伴们点点下方 👇
填空题
竞赛干货
算法竞赛字符串常用操作大全
蓝桥杯上岸必刷!!!(模拟/枚举专题)
蓝桥杯上岸必背!!! (第三期 DP)
蓝桥杯上岸必背!!!(第四期DFS)
蓝桥杯上岸必背!!!(第五期BFS)
蓝桥杯上岸必背!!!(第六期树与图的遍历)
蓝桥杯上岸必背!!!(第七期 最短路算法)
蓝桥杯上岸必背!!!(第八期 简单数论)
前言
蓝桥杯后天就要开始啦~还没刷题的同学跟我一起来刷历年真题,迟点出考前鲤鱼锦囊 🙏
喜欢的小伙伴可以关注我,关注寸铁,我们一起上岸4.8蓝桥杯!!!
求阶乘
考点:二分+反复整除法
分析
题目问我们的是满足N!的末尾恰好有K个0的最小的N是多少?
思路
阶乘数要想凑出来0必定是有若干个2、5
由于是阶乘2的个数必定是多于5的个数。
因此我们需要去枚举5的个数
没有思路怎么办?
暴力出奇迹,模拟过样例!
10!
10*9*8*7*6*5*4*3*2*1
10、5 总共是2个5
10/5=2
16!
16*15*14*...*10*...*5*...*1
15、10、5总共是3个5
16/5=3
25!
25*...*20*...*15*...*10*...*5
25、20、15、10、5总共有6个5
为什么是6个?
原因在于25可以被拆成5*5,总共是6个5。
所以我们需要反复整除5,这样才能把边界值含5的个数全部统计出来。
最后加上5的个数即可
25/5=5+5/5=6
又如125=5*5*5一共是3个5等于**125/5**
又如625=5*5*5*5一共是**4个5等于625/5**
我们通过模拟可以发现:
我们直接对枚举到的数字整除5判断
输出能整除5是k的数字即可
但是看到k的上界为1e18直接枚举必定**TLE**
题目要求满足N!的末尾恰好有K个0的最小的N
我们需要优化解决,当前N!恰好有k个0。
比N大的N!必定大于K个0,比N小的N!必定小于K个0。
我们直接想到二分来做这道题!!!
怎么二分?
不像最少刷题数那样,满足条件才能进行二分。
这道题直接枚举数字套模板进行二分即可。
因为题目问我们的是最少满足k个0的数字N是多少
不过最后还要检验一下二分出的答案是不是k个0
此外,这题需要考虑一些数据的细节
时间关系,具体看这两个大佬写的博客,写得很棒%%%
博客1
博客2
ACcode
import java.util.*;
public class Main{public static void main(String []args) {Scanner sc=new Scanner(System.in);long k=sc.nextLong();long l=1,r=(long)9e18;//数据要开大//二分while(l<r) {long mid=l+(r-l)/2;//需要再减去l//当前的N拆分成5的倍数的个数大于等于k//说明需要缩减范围,即r=midif(query(mid)>=k)r=mid;//说明不够k需要继续寻找else l=mid+1;}long x=query(r);//再查一下N是不是能被拆成k个5//可以的话输出r//不可以则输出-1if(x==k)System.out.println(r);else System.out.println("-1");}static long query(long x) {long ans=0;//统计能拆分成5的个数while(x>0) {ans+=x/5;//直接让其除以5x/=5;}return ans;}
}提炼
反复整除法:得出某个数的阶乘含a的个数
static long query(long x) {long ans=0;//统计能拆分成a的个数while(x>0) {ans+=x/a;//直接让其除以ax/=a;//再对边界x进行反复整除//统计出x还能拆成多少个5/包含多少个5}return ans;}
ACcode2
import java.util.*;
public class Main{public static void main(String []args){Scanner sc=new Scanner(System.in);long k=sc.nextLong();long l=1;long r=(long)9e18;while(l<r){long mid=l+r>>1;if(check(mid)>=k)r=mid;else l=mid+1;}long x=check(r);if(x==k)System.out.println(r);else System.out.println("-1");}public static long check(long x){long ans=0;while(x>0){ans+=x/5;x/=5;}return ans; }
}
参考资源
http://t.csdn.cn/2WxI4
https://blog.csdn.net/weixin_57943259/article/details/124206177
相关文章:
!!!)
蓝桥杯上岸每日N题 第六期(求阶乘)!!!
蓝桥杯上岸每日N题第六期 ❗️ ❗️ ❗️ 同步收录 👇 蓝桥杯上岸必背!!!(持续更新中~) 大家好 我是寸铁💪 冲刺蓝桥杯省一模板大全来啦 🔥 蓝桥杯4月8号就要开始了 🙏 距离蓝桥杯省赛倒数…...
Codeforces Round 889 (Div. 2)(视频讲解A——D)
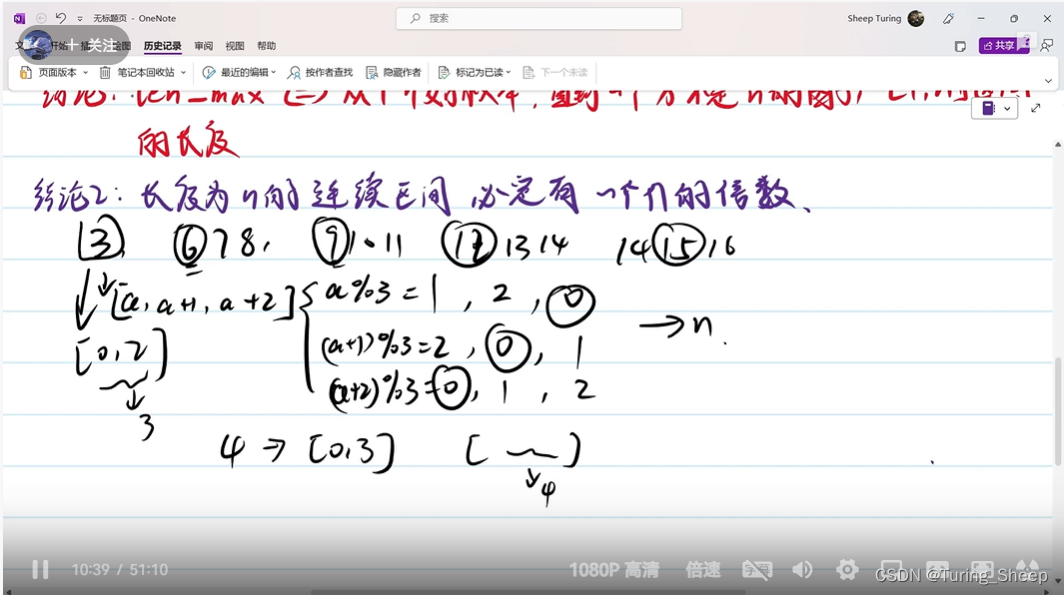
文章目录 A Dalton the TeacherB Longest Divisors IntervalC2 Dual (hard Version)D Earn or Unlock Codeforces Round 889 (Div. 2)(视频讲解A——D) A Dalton the Teacher #include<bits/stdc.h> #define endl \n #define INF 0x3f3f3f3f us…...

K8s安全配置:CIS基准与kube-bench工具
01、概述 K8s集群往往会因为配置不当导致存在入侵风险,如K8S组件的未授权访问、容器逃逸和横向攻击等。为了保护K8s集群的安全,我们必须仔细检查安全配置。 CIS Kubernetes基准提供了集群安全配置的最佳实践,主要聚焦在两个方面:主…...
linux安装python和部署Django项目
文章目录 1 python安装2 Django项目部署 1 python安装 官网地址:https://www.python.org/ 本次下载的python安装包地址:https://www.python.org/ftp/python/3.8.16/Python-3.8.16.tgz 解压下载的python压缩包 [rootlocalhost software]# tar -zxvf P…...

00-Hadoop入门
Hadoop入门 Hadoop四高 1)高可靠性 Hadoop底层维护多个数据副本,所有即使hadoop某个计算元素或存储故障,也不会造成数据丢失 2)高扩展性 在集群间分配任务数据,可方便的扩展数以千计的节点 3)高效性 …...

SE-Net注意力机制详解
📌本次任务:了解SE-Net原理 SE-Net 是 ImageNet 2017(ImageNet 收官赛)的冠军模型,是由WMW团队发布。具有复杂度低,参数少和计算量小的优点。且SENet 思路很简单,很容易扩展到已有网络结构如 Inception 和 ResNet 中。(这篇论文是2019年的,应该是后续做了更新) 一…...
商城免费搭建之java商城 开源java电子商务Spring Cloud+Spring Boot+mybatis+MQ+VR全景+b2b2c bbc
 1. 涉及平台 平台管理、商家端(PC端、手机端)、买家平台(H5/公众号、小程序、APP端(IOS/Android)、微服务平台(业务服务) 2. 核心架构 Spring Cloud、Spring Boot、Mybatis、R…...

推理加速 --- torch.compile
推理加速-- torch.compile 一、背景介绍1.2 首次推理速度慢1.3 推理多次之后,又会出现一次速度特别慢的情况,感觉好像是重新优化 二、如何使用三、其他设置3.1 mode 设置3.2 backend3.3 fullgraph3.4 dynamic 参考资料 一、背景介绍 PyTorch 2.0 官宣了…...
JS-----数据结构与算法(2)
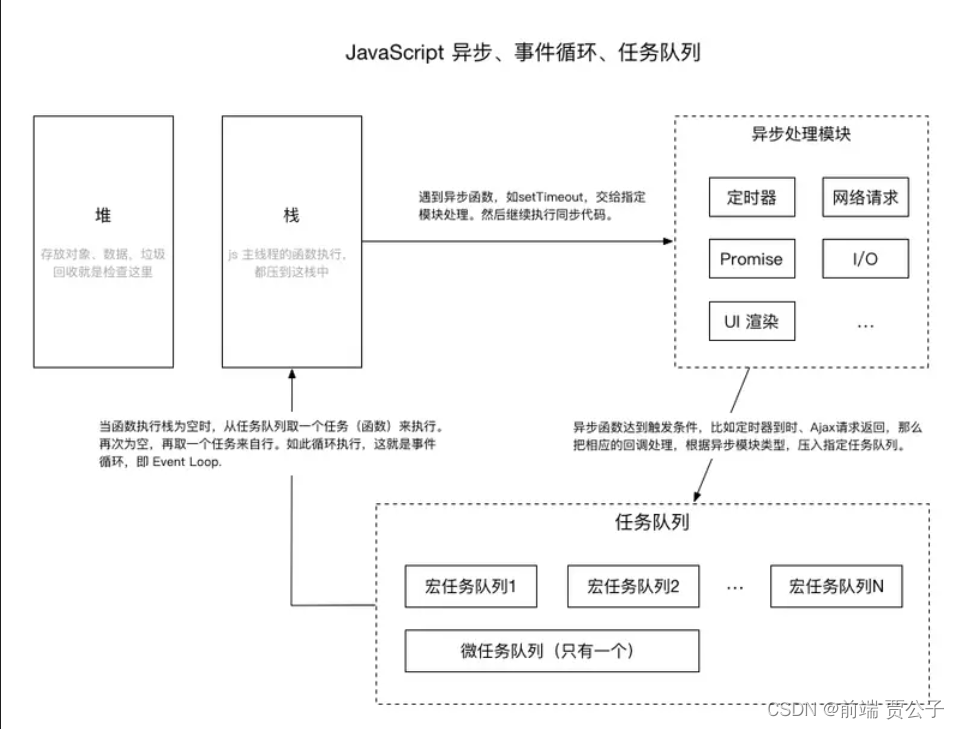
目录 三. 栈结构 1.认识栈结构 2. 封装栈结构 3. 应用 3-1 十进制转二进制 3-2 进制转换法 四. 队列 1.队列是什么? 2.队列的封装 3. 队列的应用-击鼓传花 4. 双端队列 5.判断是否为回文 三. 栈结构 1.认识栈结构 栈(stack)又…...
手把手安装TomCat;并部署JPress
目录 一、了解Tomcat: 二、安装 1、获取Tomcat软件包,且需要Java环境。 2、安装jdk 3、安装Tomcat 1.解压并创建软链接: 2.创建启动用户并更改文件权限: 3.编写系统服务文件: 4.重新加载配置文件并启动tomcat…...

tensorflow1.13分布式训练 参考资料 -教程原理
前言 对于数据量较大的时候,通过分布式训练可以加速训练。相比于单机单卡、单机多卡只需要用with tf.device(‘/gpu:0’)来指定GPU进行计算的情况,分布式训练因为涉及到多台机器之间的分工交互,所以更麻烦一些。本文简单介绍了多机(单卡/多卡…...

DP学习第五篇之礼物的最大价值
DP学习第五篇之礼物的最大价值 剑指 Offer 47. 礼物的最大价值 - 力扣(LeetCode) 一.题目解析 二. 算法原理 状态表示 tips: 经验题目要求。以[i,j]位置为结尾,。。。 dp[i][j]: 到达[i, j]位置时,此时的最大礼物价值 状态转移…...
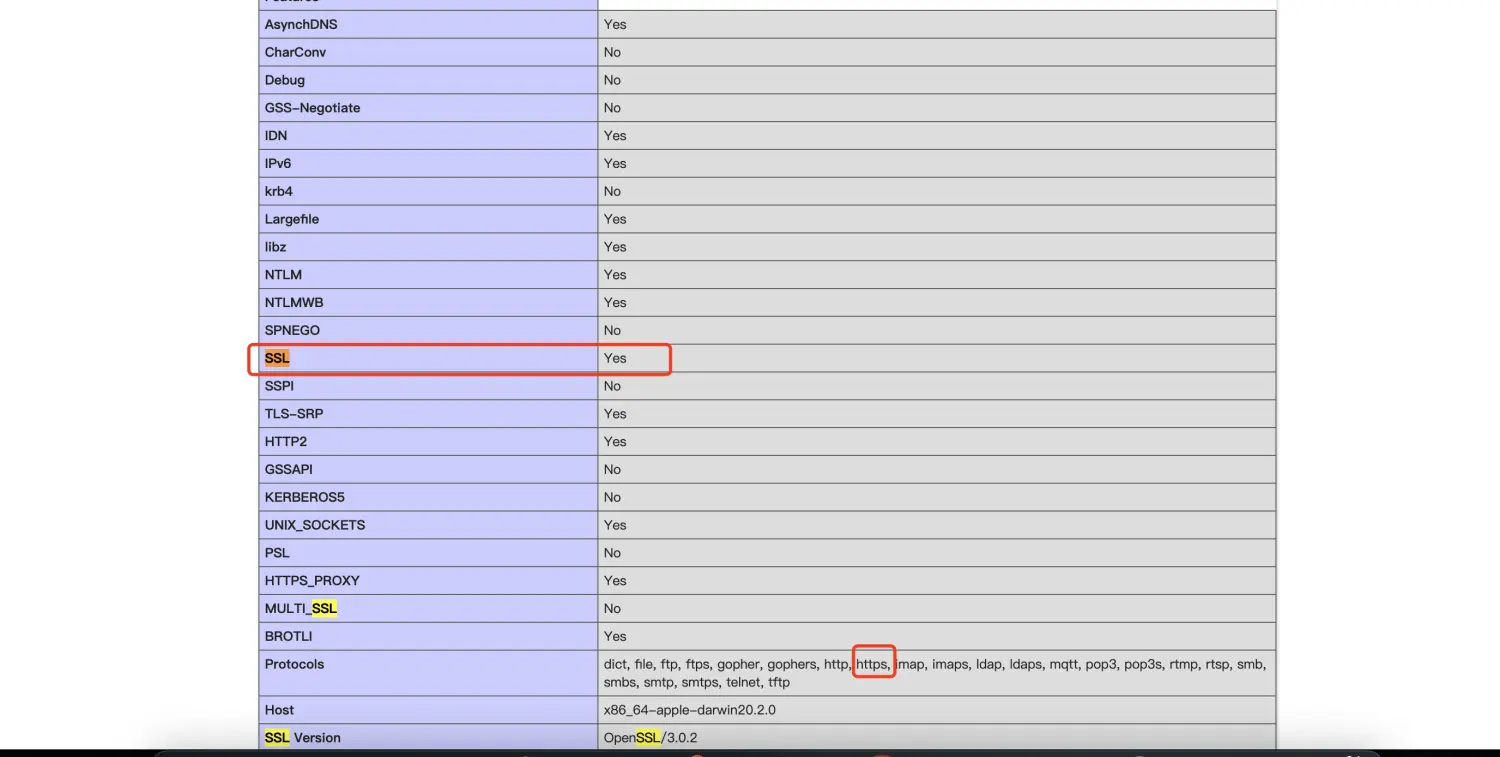
cURL error 1: Protocol “https“ not supported or disabled in libcurl
1、php项目composer update报错 2、curl -V检查 发现curl已经支持了https了 3、php版本检查 4、php插件检查 插件也已经含有openssl组件了 5、phpinfo检查 curl是否开启ssl 定位到问题所在,php7.4的 curl扩展不支持 https 需要重装 php7.4的curl扩展 6、curl下载 下…...

XCode升级后QT无法编译的问题
原因是SDK的版本变了,Qt配置的版本要修改。 解决办法如下: 1.找到 /Users/*/Qt/5.15.2/clang_64/mkspecsqdevice.pri 这个文件打开编辑, 在文件末尾追加一句 !host_build:QMAKE_MAC_SDKmacosx13.1 至于这个版本号13.1是怎么来的呢࿱…...

springboot编写mp4视频播放接口
简单粗暴方式 直接读取指定文件,用文件流读取视频文件,输出到响应中 GetMapping("/display1/{fileName}")public void displayMp41(HttpServletRequest request, HttpServletResponse response,PathVariable("fileName") String fi…...

华为OD机试真题 JavaScript 实现【机器人活动区域】【2023Q1 200分】,附详细解题思路
目录 一、题目描述二、输入描述三、输出描述四、解题思路五、JavaScript算法源码六、效果展示1、输入2、输出 华为OD机试 2023B卷题库疯狂收录中,刷题点这里 刷的越多,抽中的概率越大,每一题都有详细的答题思路、详细的代码注释、样例测试&am…...

C++中的静态分配和动态分配
为什么不是 LaoJiaHelper mydalnew LaoJiaHelper (); 而是LaoJiaHelper mydal? 这个都没有new ,对象为什么能用?在 C 中,有两种创建对象的方式:静态分配和动态分配。 静态分配: 当你使用类似 LaoJiaHelpe…...

【Android常见问题(五)】- Flutter项目性能优化
文章目录 知识回顾前言源码分析1. 渲染过程2. 分析工具3. 优化方法合理使用const关键词合理使用组件管理着色器编译垃圾 知识回顾 前言 项目迭代开发一定程度后,性能优化是重中之重,其中包括了包体积,UI 渲染、交互等多个方面。 通过 Flutt…...
)
JSON转换:实体类和JSONObject互转,List和JSONArray互转(fastjson版)
//1.java对象转化成String String sJSONObject.toJSONString(javaObject.class); //2. java对象转化成Object Object strJSONObject.toJSON(javaObject.class); //3.String类型转json对象 JSONObject jsonObject JSONObject.parseObject(str); //4. String…...

Java单例模式几种代码详解
在软件开发中,单例模式是一种常见的设计模式,它的目的是确保一个类在任何情况下都只有一个实例,同时提供一个全局访问点。在Java中,有几种常见的实现单例模式的方式,下面将逐一进行详细解释。 懒汉式(非线…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
