【机器学习】Gradient Descent
Gradient Descent for Linear Regression
- 1、梯度下降
- 2、梯度下降算法的实现
- (1) 计算梯度
- (2) 梯度下降
- (3) 梯度下降的cost与迭代次数
- (4) 预测
- 3、绘图
- 4、学习率
首先导入所需的库:
import math, copy
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')
from lab_utils_uni import plt_house_x, plt_contour_wgrad, plt_divergence, plt_gradients
1、梯度下降
使用线性模型来预测 f w , b ( x ( i ) ) f_{w,b}(x^{(i)}) fw,b(x(i)):
f w , b ( x ( i ) ) = w x ( i ) + b (1) f_{w,b}(x^{(i)}) = wx^{(i)} + b \tag{1} fw,b(x(i))=wx(i)+b(1)
在线性回归中, 利用训练数据来拟合参数 w w w, b b b,通过最小化预测值 f w , b ( x ( i ) ) f_{w,b}(x^{(i)}) fw,b(x(i)) 与实际数据 y ( i ) y^{(i)} y(i) 之间的误差来实现。 这种衡量为 cost, 即 J ( w , b ) J(w,b) J(w,b)。 在训练中,可以衡量所有样例 x ( i ) , y ( i ) x^{(i)},y^{(i)} x(i),y(i)的cost:
J ( w , b ) = 1 2 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) 2 (2) J(w,b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})^2\tag{2} J(w,b)=2m1i=0∑m−1(fw,b(x(i))−y(i))2(2)
梯度下降描述为:
repeat until convergence: { w = w − α ∂ J ( w , b ) ∂ w b = b − α ∂ J ( w , b ) ∂ b } \begin{align*} \text{repeat}&\text{ until convergence:} \; \lbrace \newline \; w &= w - \alpha \frac{\partial J(w,b)}{\partial w} \tag{3} \; \newline b &= b - \alpha \frac{\partial J(w,b)}{\partial b} \newline \rbrace \end{align*} repeatwb} until convergence:{=w−α∂w∂J(w,b)=b−α∂b∂J(w,b)(3)
其中,参数 w w w, b b b 同时更新。
梯度定义为:
∂ J ( w , b ) ∂ w = 1 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) x ( i ) ∂ J ( w , b ) ∂ b = 1 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) \begin{align} \frac{\partial J(w,b)}{\partial w} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)} \tag{4}\\ \frac{\partial J(w,b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)}) \tag{5}\\ \end{align} ∂w∂J(w,b)∂b∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))x(i)=m1i=0∑m−1(fw,b(x(i))−y(i))(4)(5)
这里的 同时 意味着在更新任何一个参数之前,同时计算所有参数的偏导数。
2、梯度下降算法的实现
包含一个特征的梯度下降算法需要三个函数来实现:
compute_gradient执行上面的等式(4)和(5)compute_cost执行上面的等式(2)gradient_descent:利用compute_gradient和compute_cost
其中,包含偏导数的 Python 变量的命名遵循以下模式: ∂ J ( w , b ) ∂ b \frac{\partial J(w,b)}{\partial b} ∂b∂J(w,b) 为 dj_db.
(1) 计算梯度
compute_gradient 实现上面的 (4) 和 (5) ,返回 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b), ∂ J ( w , b ) ∂ b \frac{\partial J(w,b)}{\partial b} ∂b∂J(w,b).
def compute_gradient(x, y, w, b): """Computes the gradient for linear regression Args:x (ndarray (m,)): Data, m examples y (ndarray (m,)): target valuesw,b (scalar) : model parameters Returnsdj_dw (scalar): The gradient of the cost w.r.t. the parameters wdj_db (scalar): The gradient of the cost w.r.t. the parameter b """# Number of training examplesm = x.shape[0] dj_dw = 0dj_db = 0for i in range(m): f_wb = w * x[i] + b dj_dw_i = (f_wb - y[i]) * x[i] dj_db_i = f_wb - y[i] dj_db += dj_db_idj_dw += dj_dw_i dj_dw = dj_dw / m dj_db = dj_db / m return dj_dw, dj_db
使用 compute_gradient 函数来找到并绘制cost函数相对于参数 w 0 w_0 w0 的一些偏导数。
plt_gradients(x_train,y_train, compute_cost, compute_gradient)
plt.show()
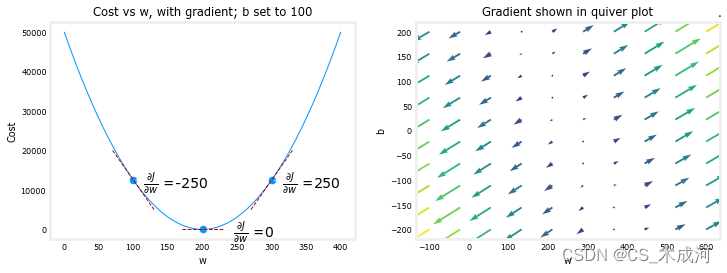
上面的左图显示了 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b),即在三个点处关于 w w w 的 cost 曲线的斜率。在图的右侧,导数为正,而在左侧为负。由于“碗形”的形状,导数将始终引导梯度下降朝着梯度为零的最低点前进。
左图中的 b b b 被固定为 100。梯度下降将同时利用 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b) 和 ∂ J ( w , b ) ∂ b \frac{\partial J(w,b)}{\partial b} ∂b∂J(w,b) 来更新参数。右侧的“矢量图”提供了查看两个参数梯度的方式。箭头的大小反映了该点梯度的大小。箭头的方向和斜率反映了该点处 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b) 和 ∂ J ( w , b ) ∂ b \frac{\partial J(w,b)}{\partial b} ∂b∂J(w,b) 的比例。梯度指向远离最小值的方向。将缩放后的梯度从当前的 w w w 或 b b b 值中减去,这将使参数朝着降低cost的方向移动。
(2) 梯度下降
现在可以计算梯度了,梯度下降方法(如上面公式(3)所描述)可以在下面的 gradient_descent 函数中实现。使用这个函数在训练数据上找到参数 w w w 和 b b b 的最优值。
def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function): """Performs gradient descent to fit w,b. Updates w,b by taking num_iters gradient steps with learning rate alphaArgs:x (ndarray (m,)) : Data, m examples y (ndarray (m,)) : target valuesw_in,b_in (scalar): initial values of model parameters alpha (float): Learning ratenum_iters (int): number of iterations to run gradient descentcost_function: function to call to produce costgradient_function: function to call to produce gradientReturns:w (scalar): Updated value of parameter after running gradient descentb (scalar): Updated value of parameter after running gradient descentJ_history (List): History of cost valuesp_history (list): History of parameters [w,b] """w = copy.deepcopy(w_in) # avoid modifying global w_in# An array to store cost J and w's at each iteration primarily for graphing laterJ_history = []p_history = []b = b_inw = w_infor i in range(num_iters):# Calculate the gradient and update the parameters using gradient_functiondj_dw, dj_db = gradient_function(x, y, w , b) # Update Parameters using equation (3) aboveb = b - alpha * dj_db w = w - alpha * dj_dw # Save cost J at each iterationif i<100000: # prevent resource exhaustion J_history.append( cost_function(x, y, w , b))p_history.append([w,b])# Print cost every at intervals 10 times or as many iterations if < 10if i% math.ceil(num_iters/10) == 0:print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e} ",f"w: {w: 0.3e}, b:{b: 0.5e}")return w, b, J_history, p_history #return w and J,w history for graphing
# initialize parameters
w_init = 0
b_init = 0
# some gradient descent settings
iterations = 10000
tmp_alpha = 1.0e-2
# run gradient descent
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha, iterations, compute_cost, compute_gradient)
print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")

从上面打印的梯度下降过程可以看出,偏导数 dj_dw和dj_db逐渐变小,开始变得很快,然后变慢。当过程接近“碗底”时,由于该点的导数值较小,进度会变慢。
(3) 梯度下降的cost与迭代次数
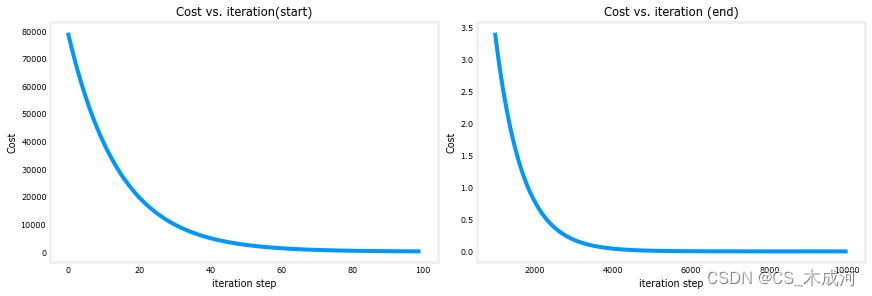
cost 与迭代次数的图是梯度下降中进展的一个有用指标。在成功的运行中,cost 应该始终降低。cost的变化在最初阶段非常迅速,因此将初始阶段的下降与最后阶段的下降绘制在不同的比例尺上是很有用的。在下面的图中,请注意坐标轴上cost的刻度和迭代步骤。
# plot cost versus iteration
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12,4))
ax1.plot(J_hist[:100])
ax2.plot(1000 + np.arange(len(J_hist[1000:])), J_hist[1000:])
ax1.set_title("Cost vs. iteration(start)"); ax2.set_title("Cost vs. iteration (end)")
ax1.set_ylabel('Cost') ; ax2.set_ylabel('Cost')
ax1.set_xlabel('iteration step') ; ax2.set_xlabel('iteration step')
plt.show()
(4) 预测
现在已经找到了参数 w w w 和 b b b 的最优值,可以使用这个模型根据学到的参数来预测房屋价格。如预期的那样,对于相同的房屋,预测值与训练值几乎相同。此外,对于没有在预测中的值,它与预期值是一致的。
print(f"1000 sqft house prediction {w_final*1.0 + b_final:0.1f} Thousand dollars")
print(f"1200 sqft house prediction {w_final*1.2 + b_final:0.1f} Thousand dollars")
print(f"2000 sqft house prediction {w_final*2.0 + b_final:0.1f} Thousand dollars")
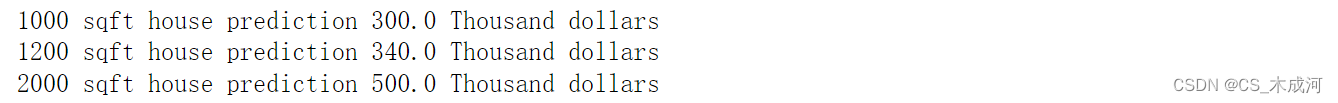
3、绘图
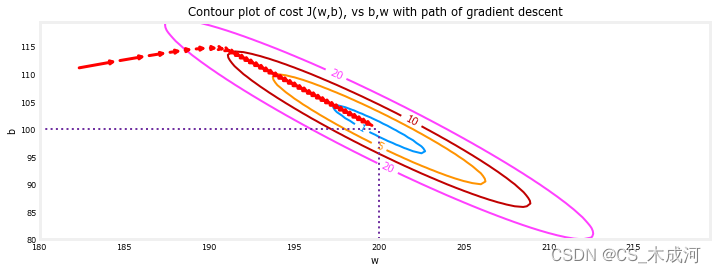
通过在cost函数的等高线图上绘制cost随迭代次数的变化来展示梯度下降执行过程。
fig, ax = plt.subplots(1,1, figsize=(12, 6))
plt_contour_wgrad(x_train, y_train, p_hist, ax)
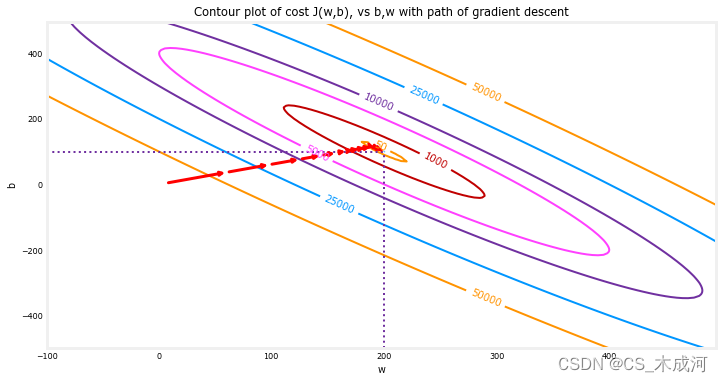
在上面的等高线图中,展示了 c o s t ( w , b ) cost(w,b) cost(w,b) 在一系列 w w w 和 b b b 值上的变化。cost 水平由环状图表示。用红色箭头叠加在图中,表示梯度下降的路径。这条路径向着目标稳步(单调地)前进,最初的步长比接近目标时的步长要大得多。
将梯度下降的最后步进行放大,随着梯度接近零,步之间的距离会缩小。
fig, ax = plt.subplots(1,1, figsize=(12, 4))
plt_contour_wgrad(x_train, y_train, p_hist, ax, w_range=[180, 220, 0.5], b_range=[80, 120, 0.5], contours=[1,5,10,20],resolution=0.5)
4、学习率
α \alpha α 越大,梯度下降就会更快地收敛到一个解。但是,如果 α \alpha α 太大,梯度下降可能会发散。上面的例子展示了一个很好地收敛的解。如果增加 α \alpha α 的值,看看会发生什么?
# initialize parameters
w_init = 0
b_init = 0
# set alpha to a large value
iterations = 10
tmp_alpha = 8.0e-1
# run gradient descent
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha, iterations, compute_cost, compute_gradient)

在上面的情况下, w w w 和 b b b 在正值和负值之间来回跳动,其绝对值在每次迭代中增加。此外,每次迭代 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b) 都会改变符号,并且cost不是减小而是增加。这明显表明学习率过大,导致解发散。通过图形来可视化这个情况。
plt_divergence(p_hist, J_hist,x_train, y_train)
plt.show()
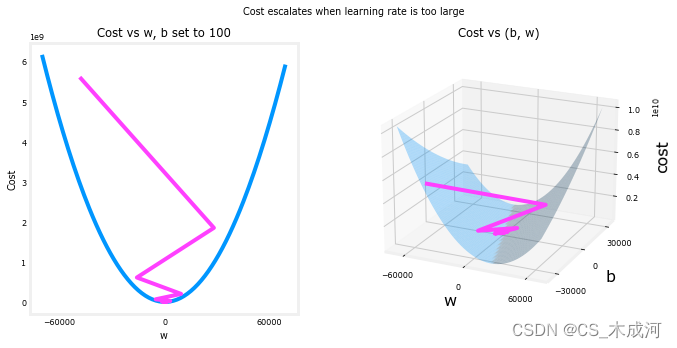
上面的左图显示了梯度下降的前几步中 w w w 的变化情况。 w w w 在正值和负值之间振荡,并且cost迅速增长。梯度下降同时对 w w w 和 b b b 进行操作,因此需要右边的三维图来得到完整的图像。
相关文章:

【机器学习】Gradient Descent
Gradient Descent for Linear Regression 1、梯度下降2、梯度下降算法的实现(1) 计算梯度(2) 梯度下降(3) 梯度下降的cost与迭代次数(4) 预测 3、绘图4、学习率 首先导入所需的库: import math, copy import numpy as np import matplotlib.pyplot as plt plt.styl…...

直播读弹幕机器人:直播弹幕采集+文字转语音(附完整代码)
目录 前言代码实现请求数据解析数据文字转语音完整代码 高级点的tk界面版 前言 直播读弹幕机器人是指能够实时读取直播平台上观众发送的弹幕,并将其转化为语音进行播放的机器人。这种机器人通常会使用文字转语音技术,将接收到的弹幕文本转为语音&#x…...

K3s vs K8s:轻量级对决 - 探索替代方案
在当今云原生应用的领域中,Kubernetes(简称K8s)已经成为了无可争议的领导者。然而,随着应用规模的不断增长,一些开发者和运维人员开始感受到了K8s的重量级特性所带来的挑战。为了解决这一问题,一个名为K3s的…...
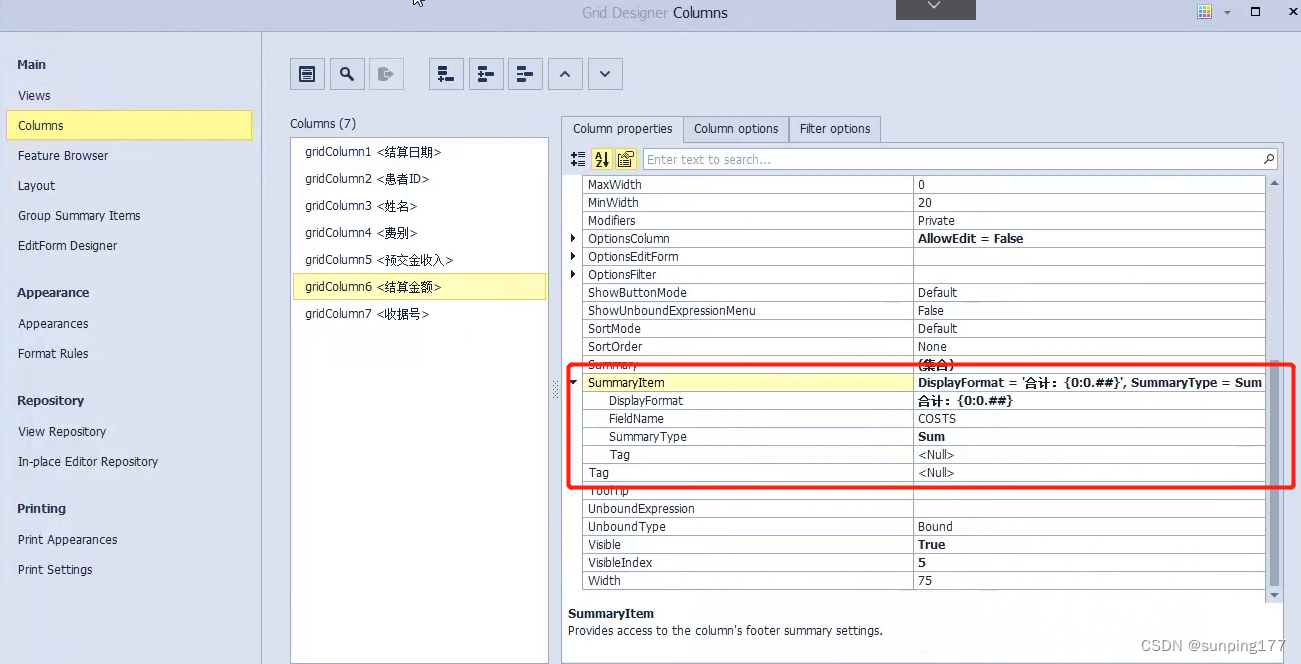
dev控件gridControl,gridview中添加合计
需求:在合并结账查询中,双击每一条结账出现这次结账对应的结算明细: 弹出的页面包括:结算日期,ID,姓名,费别,预交金收入,结算金额,收据号,合计&a…...

SpringBoot基础认识
创建SpringBoot模块 首先需要引设置maven并引用maven环境 1.打开项目结构,new module,选择Spring Initializr,URL选默认: group填写分组如com.kdy , Artifact起个模块名如springboot_quickstart,Type选择M…...
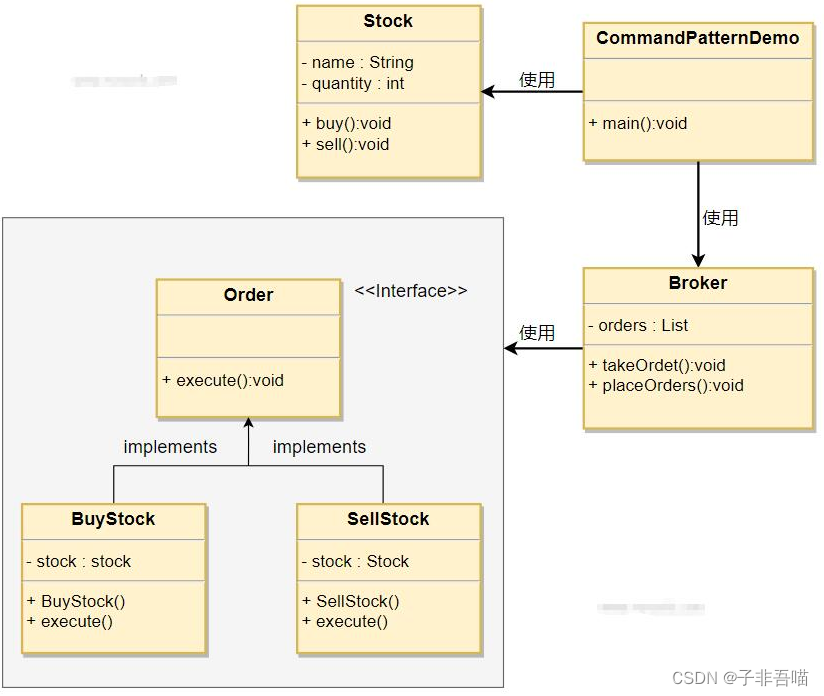
二十三种设计模式第十九篇--命令模式
命令模式是一种行为设计模式,它将请求封装成一个独立的对象,从而允许您以参数化的方式将客户端代码与具体实现解耦。在命令模式中,命令对象充当调用者和接收者之间的中介。这使您能够根据需要将请求排队、记录请求日志、撤销操作等。 命令模…...

STM32基础入门学习笔记:基础知识和理论 开发环境建立
文件目录: 一:基础知识和理论 1.ARM简介 2.STM32简介 3.STM32命名规范 4.STM32内部功能* 5.STM32接口定义 二:开发环境建立 1.开发板简介 2.ISP程序下载 3.最小系统电路 4.KEIL的安装 5.工程简介与调试流程 6.固件库的安装 7.编…...

Qt应用开发(基础篇)——数值微调输入框QAbstractSpinBox、QSpinBox、QDoubleSpinBox
目录 一、前言 二、QAbstractSpinBox类 1、accelerated 2、acceptableInput 3、alignment 4、buttonSymbols 5、correctionMode 6、frame 7、keyboardTracking 8、readOnly 9、showGroupSeparator 10、specialValueText 11、text 12、wrapping 13、信号 二、Q…...

html | 无js二级菜单
1. 效果图 2. 代码 <meta charset"utf-8"><style> .hiddentitle{display:none;}nav ul{list-style-type: none;background-color: #001f3f;overflow:hidden; /* 父标签加这个,防止有浮动子元素时,该标签失去高度*/margin: 0;padd…...
appium的基本使用
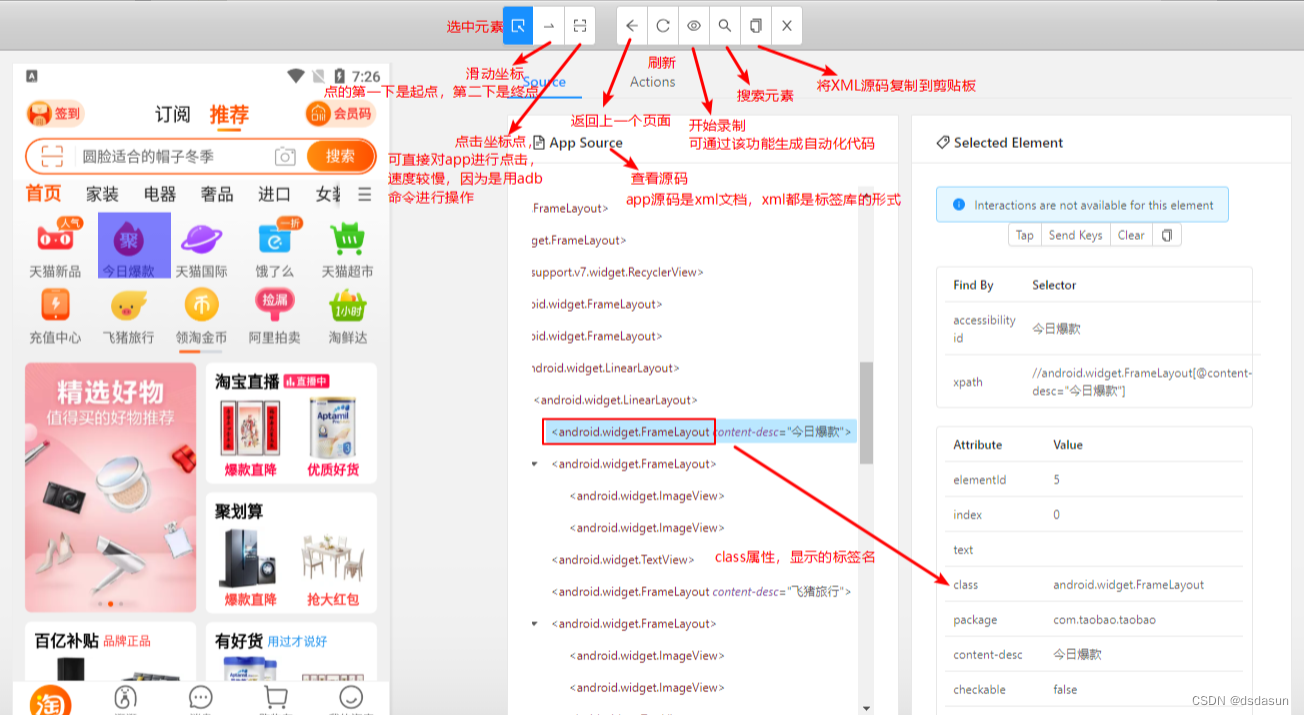
appium的基本使用 一、appium的基本使用appium环境安装1、安装Android SDK 2、安装Appium3、安装手机模拟器4、Pycharm安装 appium-python-alicent5、连接appium和模拟器6、Python代码调用appium软件,appium软件在通过adb命令调用android操作系统(模拟器…...
Dockerfile构建nginx镜像(编译安装)
Dockerfile构建nginx镜像 1、建立工作目录 [rootdocker ~]# mkdir nginx [rootdocker ~]# cd nginx/ 2、编写Dockerfile文件 [rootdocker nginx]# vim run.sh [rootdocker nginx]# vim Dockerfile #基于的基础镜像 FROM centos:7#镜像作者信息 MAINTAINER Crushlinux <…...

手机屏幕视窗机器视觉定位软硬件-康耐德
【检测目的】 手机屏幕视窗视觉定位 【效果图片】 【安装示意图】 【硬件配置】...

Databend 开源周报第 104 期
Databend 是一款现代云数仓。专为弹性和高效设计,为您的大规模分析需求保驾护航。自由且开源。即刻体验云服务:https://app.databend.cn 。 Whats On In Databend 探索 Databend 本周新进展,遇到更贴近你心意的 Databend 。 从 Kafka 载入数…...
用于医学图像分类的双引导的扩散网络
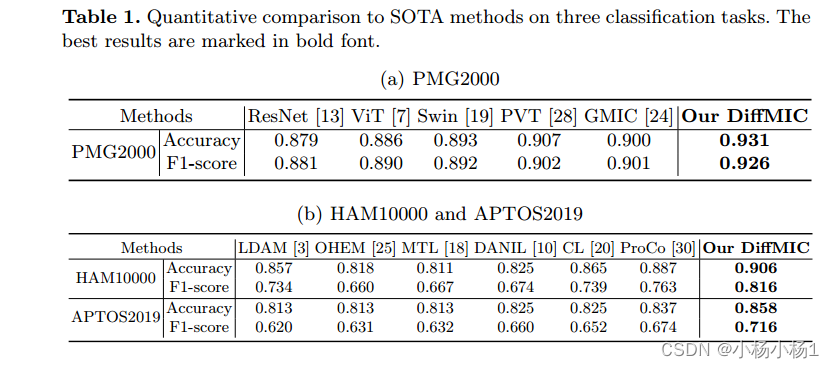
文章目录 DiffMIC: Dual-Guidance Diffusion Network for Medical Image Classification摘要本文方法实验结果 DiffMIC: Dual-Guidance Diffusion Network for Medical Image Classification 摘要 近年来,扩散概率模型在生成图像建模中表现出了显著的性能…...

8.2day03 Redis入门+解决员工模块
概述 在我们日常的Java Web开发中,无不都是使用数据库来进行数据的存储,由于一般的系统任务中通常不会存在高并发的情况,所以这样看起来并没有什么问题,可是一旦涉及大数据量的需求,比如一些商品抢购的情景࿰…...
通过案例实战详解elasticsearch自定义打分function_score的使用
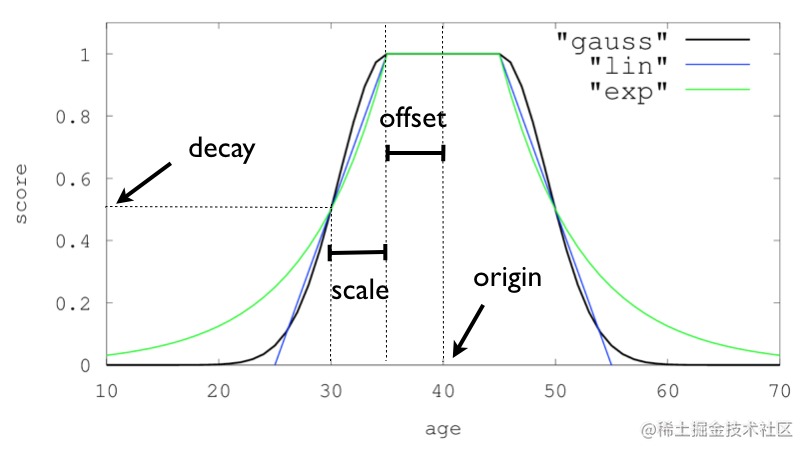
前言 elasticsearch给我们提供了很强大的搜索功能,但是有时候仅仅只用相关度打分是不够的,所以elasticsearch给我们提供了自定义打分函数function_score,本文结合简单案例详解function_score的使用方法,关于function-score-query…...
SpringBoot第28讲:SpringBoot集成MySQL - MyBatis-Plus方式
SpringBoot第28讲:SpringBoot集成MySQL - MyBatis-Plus方式 本文是SpringBoot第28讲,MyBatis-Plus(简称 MP)是一个 MyBatis的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效率而生。MyB…...

AI 绘画Stable Diffusion 研究(三)sd模型种类介绍及安装使用详解
本文使用工具,作者:秋葉aaaki 免责声明: 工具免费提供 无任何盈利目的 大家好,我是风雨无阻。 今天为大家带来的是 AI 绘画Stable Diffusion 研究(三)sd模型种类介绍及安装使用详解。 目前,AI 绘画Stable Diffusion的…...

Docker 命令没有提示信息
问题描述 提示:这里描述项目中遇到的问题: linux安装docker后发现使用docker命令没有提示功能,使用 Tab 键的时候只是提示已有的文件 解决方案: 提示:这里填写该问题的具体解决方案: Bash命令补全 Docke…...
springboot第33集:nacos图
./startup.sh -m standalone Nacos是一个内部微服务组件,需要在可信的内部网络中运行,不可暴露在公网环境,防止带来安全风险。Nacos提供简单的鉴权实现,为防止业务错用的弱鉴权体系,不是防止恶意攻击的强鉴权体系。 鉴…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
