[2023杭电多校5 1005] Snake (生成函数)
题意
有 n n n 个标号为 1 , 2 , ⋯ , n 1,2,\cdots,n 1,2,⋯,n 的球,放到 m m m 个无标号盒子 (盒内顺序有标号),且每个盒子球数不超过 k k k,求方案数对 998 244 353 998\,244\,353 998244353 取模。
1 ≤ m , k ≤ n ≤ 1 0 6 1 \le m,k \le n \le 10 ^ 6 1≤m,k≤n≤106
分析:
考虑每个盒子内球的生成函数 ∑ i = 1 k x i \sum\limits_{i = 1} ^ {k}x ^ i i=1∑kxi,那么 m m m 个盒子的生成函数就为 ( ∑ i = 1 k x i ) m \left( \sum\limits_{i = 1} ^ {k}x ^ i\right) ^ m (i=1∑kxi)m,那么方案数就为第 n n n 项系数
由于球带标号,所以需要对答案全排列,也就是乘 n ! n! n!,又由于盒子不带标号,所以要对答案除 m ! m! m!,那么答案为
n ! m ! × [ x n ] ( ∑ i = 1 k x i ) m \frac{n!}{m!} \times [x ^ n]\left( \sum\limits_{i = 1} ^ {k}x ^ i\right) ^ m m!n!×[xn](i=1∑kxi)m
1 0 6 10 ^ 6 106 用多项式快速幂会超时,考虑
( ∑ i = 1 k x i ) m = x m ( ∑ i = 0 k − 1 x i ) m = x m ( 1 − x k ) m ( 1 − x ) m \left( \sum\limits_{i = 1} ^ {k}x ^ i\right) ^ m= x ^ m \left( \sum\limits_{i = 0} ^ {k - 1}x ^ i\right) ^ m = x ^ m \frac{(1 -x ^ k)^m}{(1 - x) ^ m} (i=1∑kxi)m=xm(i=0∑k−1xi)m=xm(1−x)m(1−xk)m
转为求 [ x n − m ] ( 1 − x k ) m ( 1 − x ) m [x^{n - m}] \dfrac{(1 -x ^ k)^m}{(1 - x) ^ m} [xn−m](1−x)m(1−xk)m 其中
( 1 − x k ) m = ∑ i = 0 m ( m i ) × ( − 1 ) i × x i × k 1 ( 1 − x ) m = ∑ i = 0 ∞ ( m − 1 + i m − 1 ) × x i (1 - x ^ k) ^ m = \sum_{i = 0} ^ {m}\binom{m}{i} \times (-1) ^ i \times x ^ {i \times k} \\ \frac{1}{(1 - x) ^ m} = \sum_{i = 0} ^ {\infty} \binom{m - 1 + i}{m - 1} \times x ^ i (1−xk)m=i=0∑m(im)×(−1)i×xi×k(1−x)m1=i=0∑∞(m−1m−1+i)×xi
于是枚举第一个式子的 i i i,那么只需要求第二个式子的 n − m − i × k n - m - i \times k n−m−i×k 项系数即可。预处理组合数即可。
代码:
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
constexpr int mod = 998244353;
template<class T>
T power(T a, int b) {T res = 1;for (; b; b /= 2, a *= a) {if (b % 2) {res *= a;}}return res;
}
template<int mod>
struct ModInt {int x;ModInt() : x(0) {}ModInt(i64 y) : x(y >= 0 ? y % mod : (mod - (-y) % mod) % mod) {}ModInt &operator+=(const ModInt &p) {if ((x += p.x) >= mod) x -= mod;return *this;}ModInt &operator-=(const ModInt &p) {if ((x += mod - p.x) >= mod) x -= mod;return *this;}ModInt &operator*=(const ModInt &p) {x = (int)(1LL * x * p.x % mod);return *this;}ModInt &operator/=(const ModInt &p) {*this *= p.inv();return *this;}ModInt operator-() const {return ModInt(-x);}ModInt operator+(const ModInt &p) const {return ModInt(*this) += p;}ModInt operator-(const ModInt &p) const {return ModInt(*this) -= p;}ModInt operator*(const ModInt &p) const {return ModInt(*this) *= p;}ModInt operator/(const ModInt &p) const {return ModInt(*this) /= p;}bool operator==(const ModInt &p) const {return x == p.x;}bool operator!=(const ModInt &p) const {return x != p.x;}ModInt inv() const {int a = x, b = mod, u = 1, v = 0, t;while (b > 0) {t = a / b;swap(a -= t * b, b);swap(u -= t * v, v);}return ModInt(u);}ModInt pow(i64 n) const {ModInt res(1), mul(x);while (n > 0) {if (n & 1) res *= mul;mul *= mul;n >>= 1;}return res;}friend ostream &operator<<(ostream &os, const ModInt &p) {return os << p.x;}friend istream &operator>>(istream &is, ModInt &a) {i64 t;is >> t;a = ModInt<mod>(t);return (is);}int val() const {return x;}static constexpr int val_mod() {return mod;}
};
using Z = ModInt<mod>;
vector<Z> fact, infact;
void init(int n) {fact.resize(n + 1), infact.resize(n + 1);fact[0] = infact[0] = 1;for (int i = 1; i <= n; i ++) {fact[i] = fact[i - 1] * i;}infact[n] = fact[n].inv();for (int i = n; i; i --) {infact[i - 1] = infact[i] * i;}
}
Z C(int n, int m) {if (n < 0 || m < 0 || n < m) return Z(0);return fact[n] * infact[n - m] * infact[m];
}
void solve() {int n, m, k;cin >> n >> m >> k;Z ans;for (int i = 0; i <= m; i ++) {Z f = i & 1 ? Z(-1) : Z(1);ans += f * C(m, i) * C(n - k * i - 1, m - 1);}cout << ans * fact[n] / fact[m] << "\n";
}
signed main() {init(1e6);cin.tie(0) -> sync_with_stdio(0);int T;cin >> T;while (T --) {solve();}
}
相关文章:
)
[2023杭电多校5 1005] Snake (生成函数)
题意 有 n n n 个标号为 1 , 2 , ⋯ , n 1,2,\cdots,n 1,2,⋯,n 的球,放到 m m m 个无标号盒子 (盒内顺序有标号),且每个盒子球数不超过 k k k,求方案数对 998 244 353 998\,244\,353 998244353 取模。 1 ≤ m , k ≤ n ≤ 1 0 6 1 \le…...
【MyBtis】各种查询功能
目录 【MyBtis】配置和映射 11.1 示例:实现表数据的增、删、改、查 1.创建工程mybatis_DML demo 2.创建数据库操作的工具类:DBOperatorMgr.java 3.创建映射接口 4.创建XML映射文件 5.测试 【MyBtis】配置和映射 MyBatis 的真正强大之外在于它的映射语句…...

H5打包封装小程序系统开发
H5打包封装小程序系统开发 H5打包封装小程序系统开发是指将H5页面打包封装成小程序的开发过程。下面是一个简单的步骤: 准备工作:首先,需要准备好H5页面的代码和资源文件。确保H5页面在浏览器中正常运行,并且没有依赖于浏览器特…...

SpringBoot集成jasypt,加密yml配置文件
SpringBoot集成jasypt,加密yml配置文件 一、pom配置二、生成密文代码三、配置3.1、yml加密配置3.2、密文配置3.3、启动配置3.4、部署配置 四、遇到的一些坑 最新项目安全检测,发现配置文件中数据库密码,redis密码仍处理明文状态 一、pom配置…...
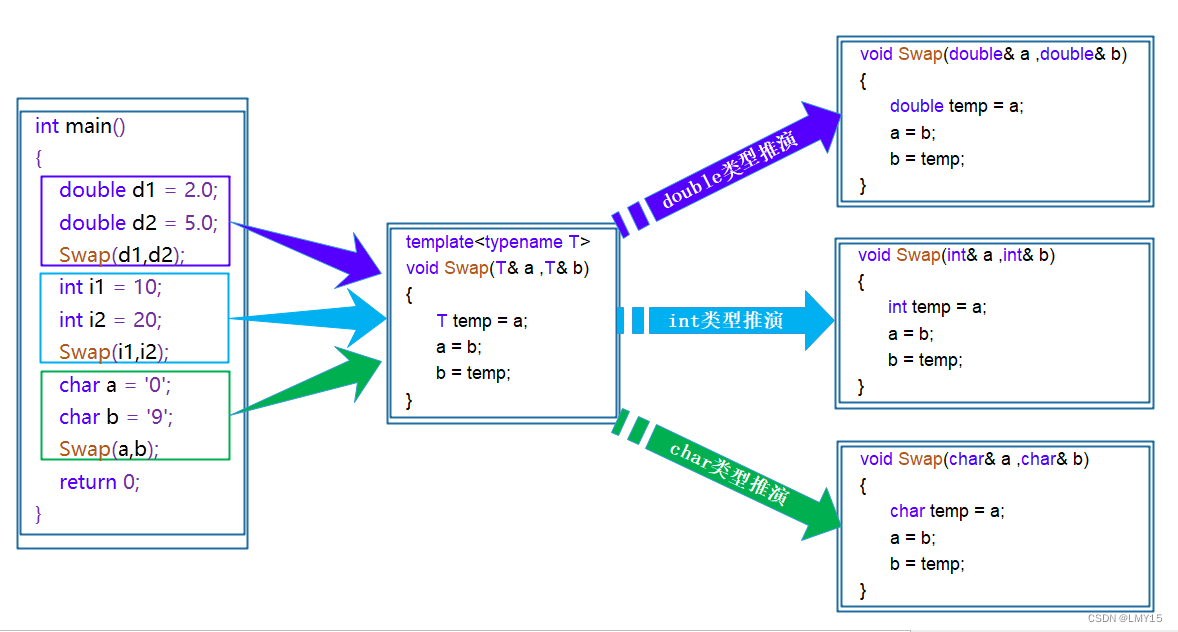
【C++】模板(初阶)
1、泛型编程 泛型编程:编写与类型无关的通用代码,是代码复用的一种手段。模板是泛型编程的基础 2、函数模板 函数模板代表了一个函数家族,该函数模板与类型无关,在使用时被参数化,根据实参类型产生函数的特定类型版本…...
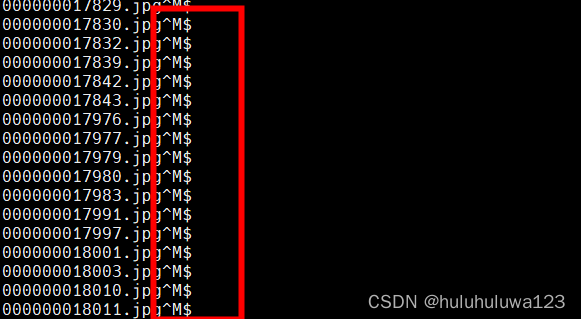
windows下的txt文档,传到ubuntu后,每行后面出现^M,怎么处理?
问题背景:windows下pycharm生成的txt文档,传到ubuntu后,每行后面出现^M 用vim打开显示 使用cat -A filename显示如下 参考https://www.lmlphp.com/user/16697/article/item/579325/给出的几种方法 方法一、dos2unix filename。服务器没装…...
LabVIEW FPGA开发实时滑动摩擦系统
LabVIEW FPGA开发实时滑动摩擦系统 由于非线性摩擦效应的建模和补偿的固有困难,摩擦系统的运动控制已被广泛研究。最近,人们更加关注滑动动力学和滑动定位,作为传统机器人定位的低成本和更灵活的驱动替代方案。摩擦控制器设计和适当选择基础…...

Prometheus服务器、Prometheus被监控端、Grafana、Prometheus服务器、Prometheus被监控端、Grafana
day03 day03Prometheus概述部署Prometheus服务器环境说明:配置时间安装Prometheus服务器添加被监控端部署通用的监控exporterGrafana概述部署Grafana展示node1的监控信息监控MySQL数据库配置MySQL配置mysql exporter配置mysql exporter配置prometheus监控mysql自动…...
)
常见的锁策略(面试八股文)
1.乐观锁vs悲观锁 乐观锁:预测该场景中不太会出现锁冲突的情况。(后续做的工作会更少) 悲观锁:预测该场景非常容易出现锁冲突(后续做的工作会更多) 锁冲突:多个线程同时尝试去获得同一把锁&…...

SO_KEEPALIVE、TCP_KEEPIDLE、TCP_KEEPINTVL、保活包
SO_KEEPALIVE SO_KEEPALIVE 是一个套接字选项,用于设置是否启用 keepalive 机制。在这段代码中没有涉及到 SO_KEEPALIVE 选项的设置。 当 SO_KEEPALIVE 被设置为非零值时,表示启用 keepalive 机制。keepalive 是一种用于检测连接是否仍然有效的机制。通…...

【phaser微信抖音小游戏开发005】画布上添加图片
特别注意:真机模拟的时候,尽量使用网络图片资源,不要在小程序源文件里面使用图片,会出现真机加载不成功,小程序包体积过大的问题。我们学习过程中,只是作为演示使用。 推荐使用场景: 背景图片…...

【设计模式——学习笔记】23种设计模式——外观模式Facade(原理讲解+应用场景介绍+案例介绍+Java代码实现)
文章目录 案例引入介绍基本介绍类图出场角色 案例实现案例一类图代码实现 案例二类图代码实现 外观模式在Mybatis源码中的应用总结文章说明 案例引入 在家庭影院中,要享受一场电影,需要如下步骤: 直接用遥控器:统筹各设备开关开…...

消息队列 -提供上层服务接口
目录 前言封装数据库封装内存操作内存的设计思想 应答模式 代码实现测试代码 前言 我们之前已经将 数据库 的操作 和文件的操作 都完成了, 但是对于上层调用来说, 并不关心是于数据库中存储数据还是往文件中存储数据, 因此 我们提供一个类, 封装一下 上述俩个类中的操作, 并将…...
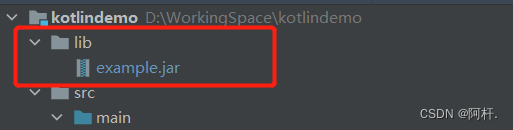
maven引入本地jar包的简单方式【IDEA】【SpringBoot】
前言 想必点进来看这篇文章的各位,都是已经习惯了Maven从中央仓库或者阿里仓库直接拉取jar包进行使用。我也是🤡🤡。 前两天遇到一个工作场景,对接三方平台,结果对方就是提供的一个jar包下载链接,可给我整…...
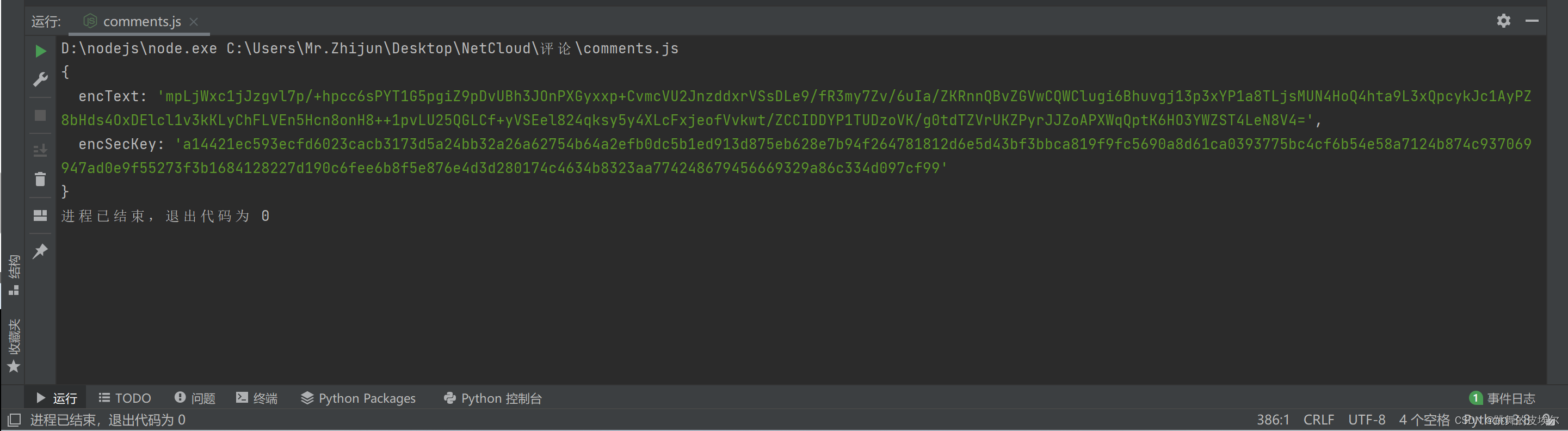
【爬虫逆向案例】某易云音乐(评论)js逆向—— params、encSecKey解密
声明:本文只作学习研究,禁止用于非法用途,否则后果自负,如有侵权,请告知删除,谢谢! 【爬虫逆向案例】某易云音乐(评论)js逆向—— params、encSecKey解密 1、前言2、行动…...

【uni-app】【Android studio】手把手教你运行uniapp项目到Android App
运行到Android App基座 选择运行到Android App基座 选择运行项目 1、连接手机,在手机上选择 传输文件。 2、打开 设置-> 关于本机 -> 版本信息->连续点击4-5次版本号 ,输入手机密码,系统就进入了开发者模式。 3、设置 > 其他设…...
多线程(JavaEE初阶系列6)
目录 前言: 1.什么是线程池 2.标准库中的线程池 3.实现线程池 结束语: 前言: 在上一节中小编带着大家了解了一下Java标准库中的定时器的使用方式并给大家实现了一下,那么这节中小编将分享一下多线程中的线程池。给大家讲解一…...

shell清理redis模糊匹配的多个key
#!/bin/bash# 定义Redis服务器地址和端口 REDIS_HOST"localhost" REDIS_PORT6380# 获取匹配键的数量 function get_matching_keys() {local key_pattern"$1"redis-cli -h $REDIS_HOST -p $REDIS_PORT -n 0 KEYS "$key_pattern" }# 删除匹配的键 …...
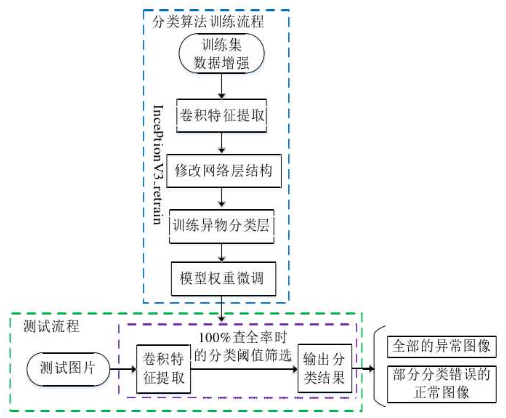
【电网异物检测硕士论文摘抄记录】电力巡检图像中基于深度学习的异物检测方法研究
根据国家电力行业发展报告统计,截止到 2018 年,全国电网 35 千伏及以上的输电线路回路长度达到 189 万千米,220 千伏及以上输电线路回路长度达73 万千米。截止到 2015年,根据国家电网公司的统计 330 千伏及以上输电线路故障跳闸总…...
C++共享数据的保护
虽然数据隐藏保护了数据的安全性,但各种形式的数据共享却又不同程度地破坏了数据的安全。因此,对于既需要共享有需要防止改变的数据应该声明为常量。因为常量在程序运行期间不可改变,所以可以有效保护数据。 1.常对象 常对象:它…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...
