剑指offer19.正则表达式

这道题我一看就有印象,我室友算法课设抽到这题,他当时有个bug让我帮他看一下,然后我就大概看了一下他的算法,他是用动态规划写的,用了一个二维数组,然后我就试着按照这个思路去写,想了一会还是没有思路,就看题解了:
class Solution {public boolean isMatch(String s, String p) {// .可以代替所有字符,*前面的一个字符可以出现任意次包括0次int m = s.length();int n = p.length();boolean[][] dp = new boolean[m+1][n+1];dp[0][0] = true;for(int i =0; i<=m; i++){for(int j=1;j<=n;j++){if(p.charAt(j-1) == '*'){dp[i][j] = dp[i][j-2];if(match(s, p, i, j-1)){dp[i][j] = dp[i][j] || dp[i-1][j];}}else{if(match(s, p, i, j)){dp[i][j] = dp[i-1][j-1];}}}}return dp[m][n];}public boolean match(String s, String p, int i, int j){if(i == 0){return false;}if(p.charAt(j-1) == '.'){return true;}return s.charAt(i-1) == p.charAt(j-1);}}dp[i][i]表示s的前i个字符与p的前j个是否匹配,进行状态转移时考虑p的第j个字符:
1,如果第j个字符是一个字母,那么必须在s中匹配一个相同的小写字母。

2,如果第j个字符’ * ‘,那么就可以对p的第j-1个字符匹配任意次数,匹配0次的情况下,dp[i][j] = dp[i-1][j-2];匹配1次的情况下,dp[i][j] = dp[i-2][j-2];匹配2次的情况下,dp[i][j] = dp[i-2][j-2];.......

所以综合两种情况有:
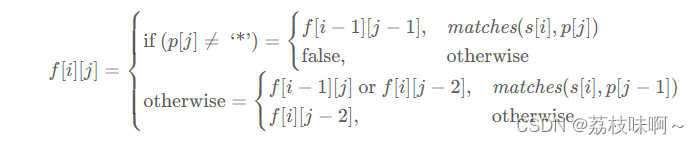
matches()是判断两个字符是否匹配的方法,如果字符相同或者模板中的字符是' . '就返回true否则返回false。
dp[0][0] = true,当两个字符是空字符时返回true,最后返回dp[m][n],m是s的长度,n是p的长度。
相关文章:
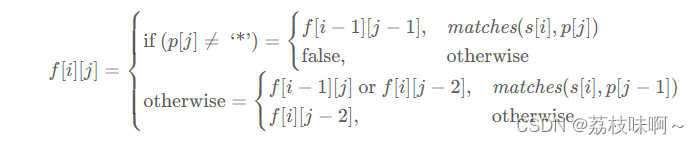
剑指offer19.正则表达式
这道题我一看就有印象,我室友算法课设抽到这题,他当时有个bug让我帮他看一下,然后我就大概看了一下他的算法,他是用动态规划写的,用了一个二维数组,然后我就试着按照这个思路去写,想了一会还是没…...

Mac Navicat 16试用脚本
一、无限试用脚本如下 #!/bin/bash #/usr/libexec/PlistBuddy -c "print" ~/Library/Preferences/com.navicat.NavicatPremium.plist /usr/libexec/PlistBuddy -c "Delete :91F6C435D172C8163E0689D3DAD3F3E9" ~/Library/Preferences/com.navicat.Navica…...
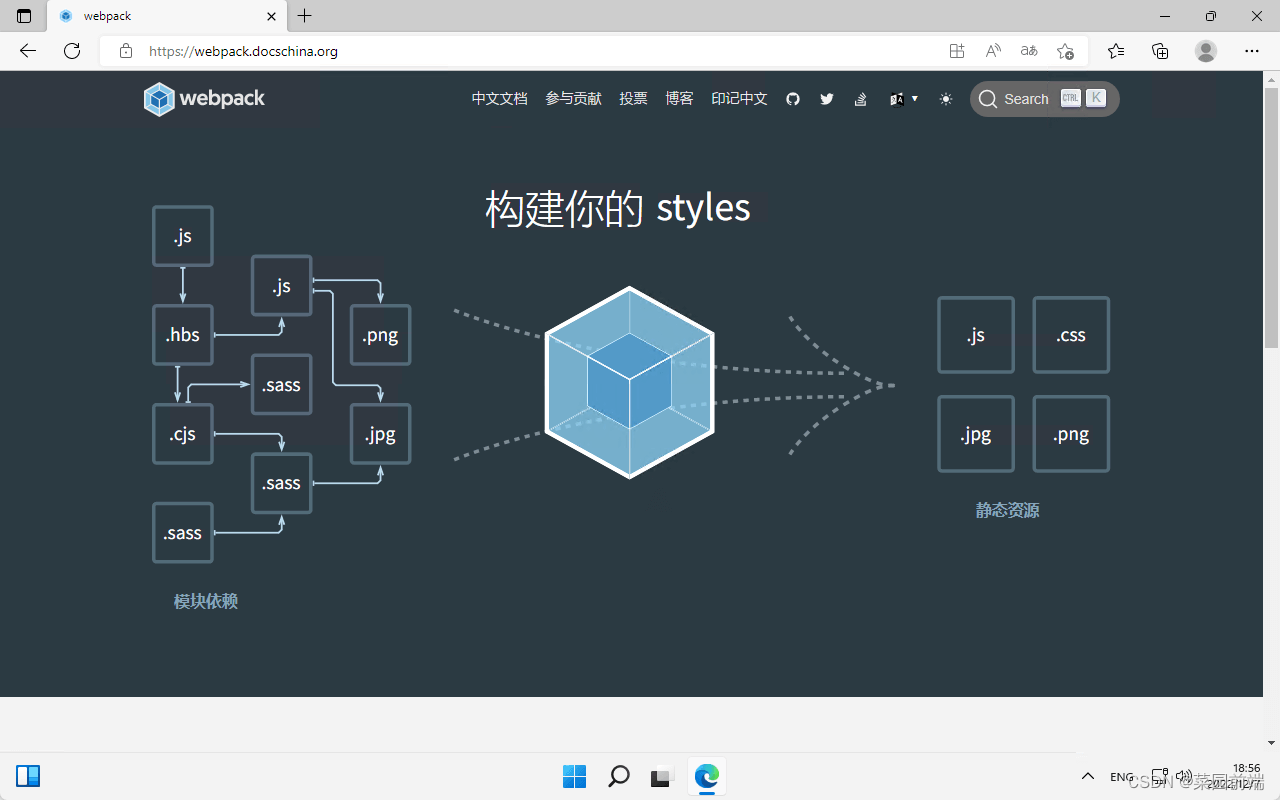
什么是 webpack?
Webpack 介绍 什么是 webpack? :::tip 官方描述 webpack 是一个用于现代 JavaScript 应用程序的静态模块打包工具。当 webpack 处理应用程序时,它会在内部从一个或多个入口点构建一个 依赖图(dependency graph),然后将你项目中所需的每一个…...

#B. 费解的开关
题目描述 你玩过“拉灯”游戏吗?2525盏灯排成一个5x55x5的方形。每一个灯都有一个开关,游戏者可以改变它的状态。每一步,游戏者可以改变某一个灯的状态。游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应…...

Docker离线安装
Docker离线安装 一、安装步骤 1. 下载 Docker 二进制文件(离线安装包) 下载地址:https://download.docker.com/linux/static/stable/x86_64/ 注:本文使用 /x86_64/docker-18.06.1-ce.tgz,注意对应操作系统类型。 2.…...
)
React高阶学习(二)
目录 1. 基本概念和语法2. 组件化开发3. 状态管理4. 生命周期钩子5. 条件渲染6. 循环渲染7. 事件处理8. 组件间通信9. 动画效果10. 模块化开发 1. 基本概念和语法 React 是基于 JavaScript 的库,用于构建用户界面。它采用虚拟 DOM 技术,能够高效地渲染页…...

C语言中的字符串输入操作详解
C语言输入字符串详解 目录 介绍使用scanf_s输入字符串scanf_s的限制和问题解决输入空格的方法——使用gets_s函数gets_s函数的注意事项示例代码演示总结 1. 介绍 在C语言中,输入字符串是常见的操作。本篇博客将详细讨论在C语言中输入字符串的方法。我们将使用s…...
C高级 DAY1
1.思维导图 二、 网络配置 更新资源库 在线下载 卸载安装包 离线下载 离线安装包卸载 cat echo head tail 管道符 字体变色 find file grep cut 截取字符 chown ln硬链接 软链接 压缩、解压缩 打包并压缩,解压缩...
)
centos7 默认路由顺序调整(IPV4_ROUTE_METRIC)
1、问题说明 A服务器有两张网卡,A1对应公网,A2对应私网,公网访问时,访问异常,内网访问服务则显示正常。 问题判断:数据包从公网进来时,路由无需判断,但数据包出去时,有…...
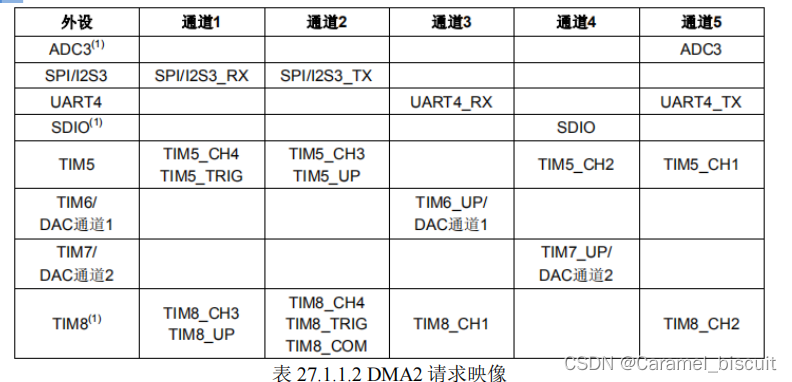
STM32 DMA学习
DMA简称 DMA,Direct Memory Access,即直接存储器访问。DMA传输方式无需CPU直接控制传输,也没有中断处理方式那样保留现场和恢复现场的过程,通过硬件为RAM与I/O设备开辟一条直接传送数据的通路,能使CPU的效率大为提高。…...

32.利用fmincon 解决 最小费用问题(matlab程序)
1.简述 fmincon函数非线性约束下的最优化问题 fmincon函数,既是求最小约束非线性多变量函数 该函数被用于求如下函数的最小值 语法如下: x fmincon(fun,x0,A,b) x fmincon(fun,x0,A,b,Aeq,beq) x fmincon(fun,x0,A,b,Aeq,beq,lb,ub) x fmincon(fun,x0,A,b,Aeq…...

Delphi 开发的QR二维码生成工具,开箱即用
目录 一、基本功能: 二、使用说明: 三、操作演示gif 四、下载链接 在日常的开发中,经常需要将一个链接生成为二维码图片,特别是在进行支付开发的时候,因为我们支付后台获取了支付链接,需要变成二维码扫…...

Springboot使用AOP编程简介
AOP简介 AOP(面向切面编程)是一种编程范式,Spring AOP是基于代理模式的AOP框架,它通过动态代理实现切面的织入,更加轻量级和易于使用。 Joinpoint (连接点):类里面可以被增强的方法即为连接点。例如,想修…...
Android性能优化—卡顿分析与布局优化
一、什么是卡顿?或者说我们怎么感知APP卡顿? 这里面涉及到android UI渲染机制,我们先了解一下android UI是怎么渲染的,android的View到底是如何一步一步显示到屏幕上的? android系统渲染页面流程: 1&…...
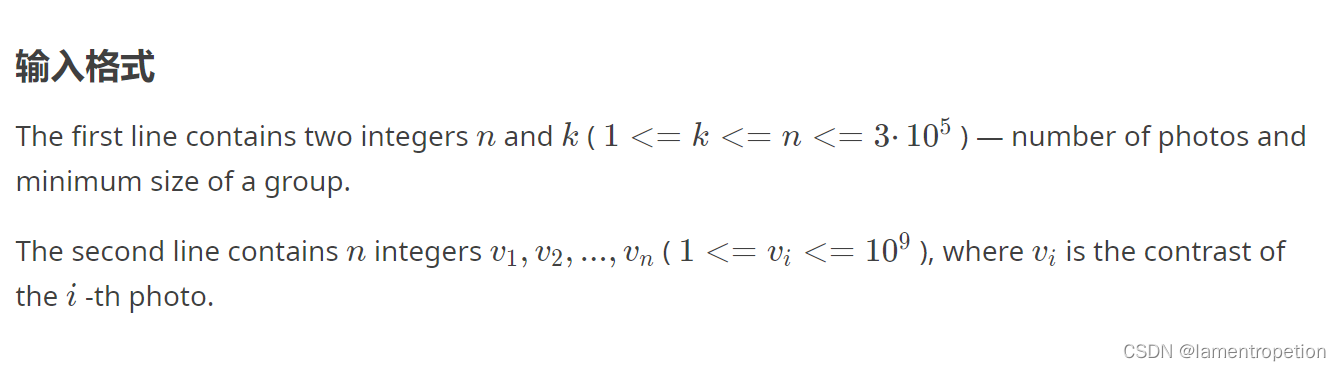
【二分+滑动窗口优化DP】CF883 I
Problem - 883I - Codeforces 题意: 思路: 首先,要让最大值最小,很显然要二分 那么就相当于有了一个极差的限制,看能不能分组,每组至少m个元素 那么就是考虑分段DP,直接n^2很容易写 但是n …...

4.netty源码分析
1.pipeline调用handler的源码 //pipeline得到双向链表的头,next到尾部, 2.心跳源码 主要分析IdleStateHandler3个定时任务内部类 //考虑了网络传输慢导致出站慢的情况 //超时重新发送,然后关闭 ReadTimeoutHandler(继承IdleStateHandler 直接关闭连接)和WriteTimeoutHandler(继…...
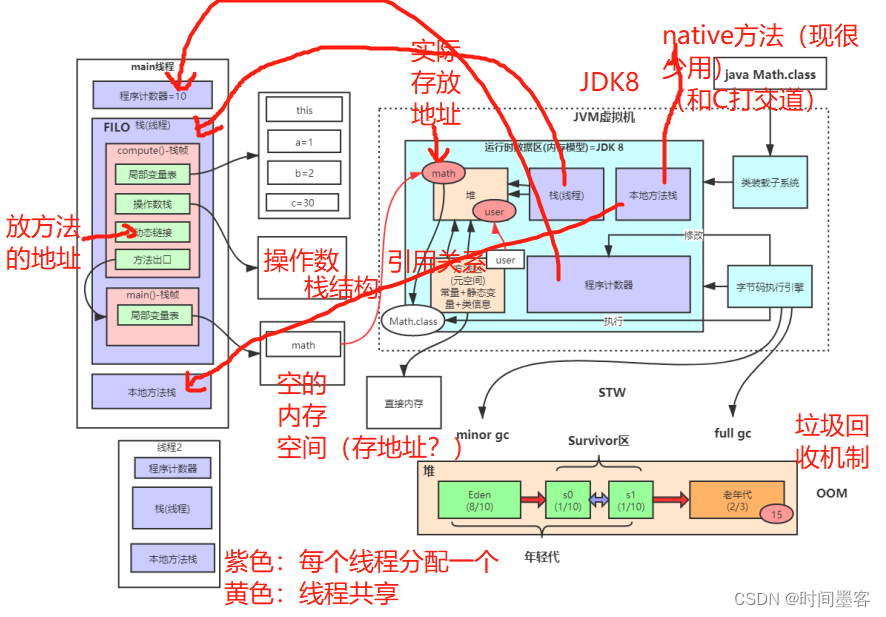
性能优化点
Arts and Sciences - Computer Science | myUSF 索引3层(高度为3)一般对于数据库地址千万级别的表 大于2000万的数据进行分库分表存储 JVM整体结构及内存模型 JVM调优:主要为减少FULL GC的执行次数或者减少FULL GC执行时间 Spring Boot程序…...
)
leetcode301. 删除无效的括号(java)
删除无效的括号 leetcode301. 删除无效的括号题目描述暴力搜索 剪枝代码演示 回溯算法 leetcode301. 删除无效的括号 难度 困难 https://leetcode.cn/problems/remove-invalid-parentheses/description/ 题目描述 给你一个由若干括号和字母组成的字符串 s ,删除最小…...
快速制作美容行业预约小程序
随着科技的不断进步,移动互联网的快速发展,小程序成为了很多行业迅速发展的利器。对于美容行业来说,一款美容预约小程序不仅可以方便用户进行预约,还可以提升美容店铺的服务质量和管理效率。下面,我们来介绍一下如何快…...

Golang之路---03 面向对象——结构体
结构体 结构体定义 在之前学过的数据类型中,数组与切片,只能存储同一类型的变量。若要存储多个类型的变量,就需要用到结构体,它是将多个任意类型的变量组合在一起的聚合数据类型。 每个变量都成为该结构体的成员变量。 可以理…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
