【C++】AVL树和红黑树(插入和测试详解)
文章目录
- 1、AVL树
- 1.1 AVL树的插入
- 1.2 总结与测试AVL树
- 2、红黑树
- 2.1 红黑树的插入
- 2.2 红黑树的测试
了解AVL树是为了了解红黑树,了解红黑树是为了更好的理解set和map。
1、AVL树
AVL树是在二叉搜索树的基础上进行了严格的平衡,能做到平衡的关键是通过平衡因子以及旋转。
AVL树有以下特性:
- 任何根的左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)。
- 其中平衡因子是用右子树高度减去左子树高度。
- 任何子树都是AVL树。
下面实现的AVL树还是KV结构的。
AVL树节点定义
#include <iostream>
#include <assert.h>
using namespace std;template<class K, class V>
struct AVLTreeNode
{//三叉链结构方便访问父节点struct AVLTreeNode<K, V>* _left;struct AVLTreeNode<K, V>* _right;struct AVLTreeNode<K, V>* _parent;pair<K, V> _kv; //键值对 里面存储key和valueint _bf; //平衡因子AVLTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0)
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:private:Node* root = nullptr;
};
1.1 AVL树的插入
1、AVL树的插入首先一开始和二叉搜索树的插入一样,先确定插入的位置,再和父节点链接。
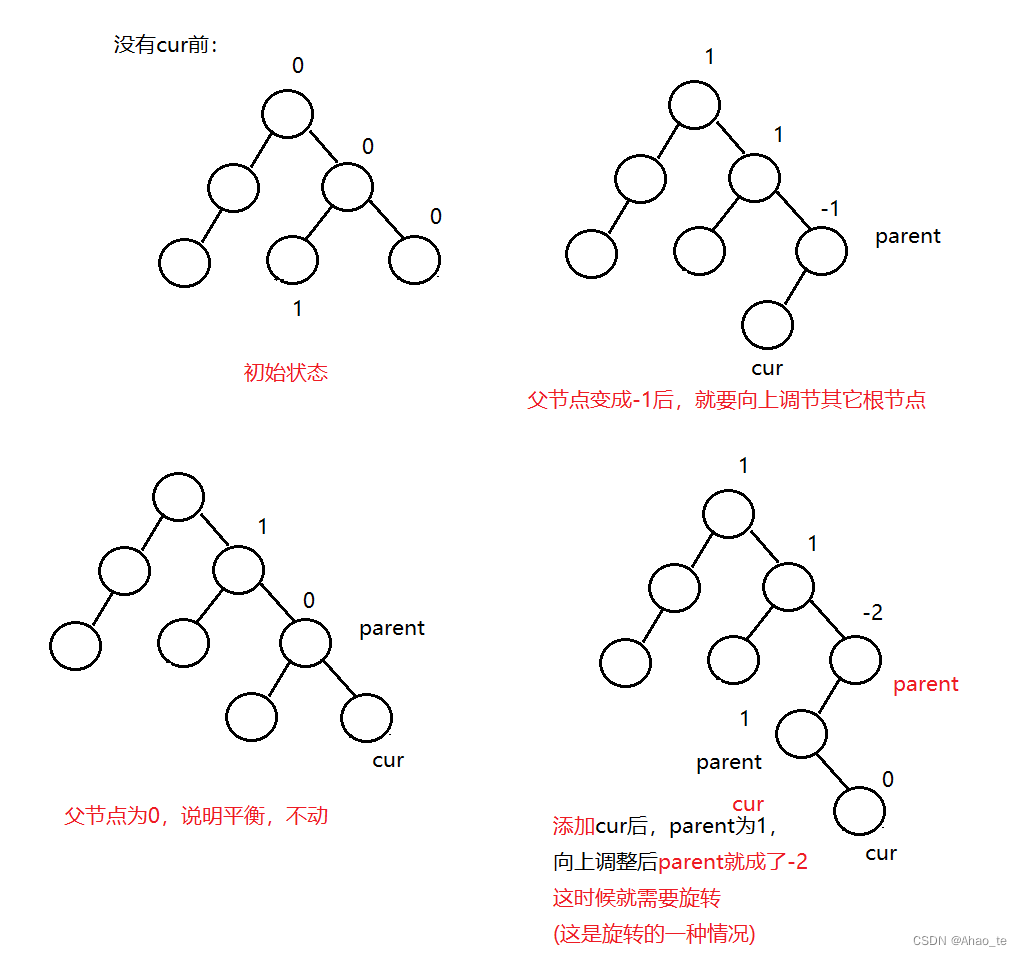
2、插入完后,可能会破坏AVL树结构,所以要判断平衡因子。
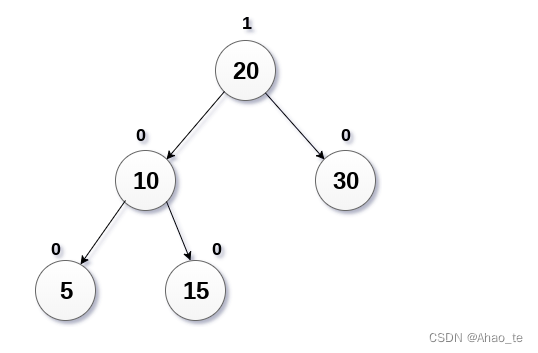
插入新结点后,平衡因子会出现三种情况。
3、当平衡因子出现了-2或2的情况,这个时候就需要对parent进行旋转。
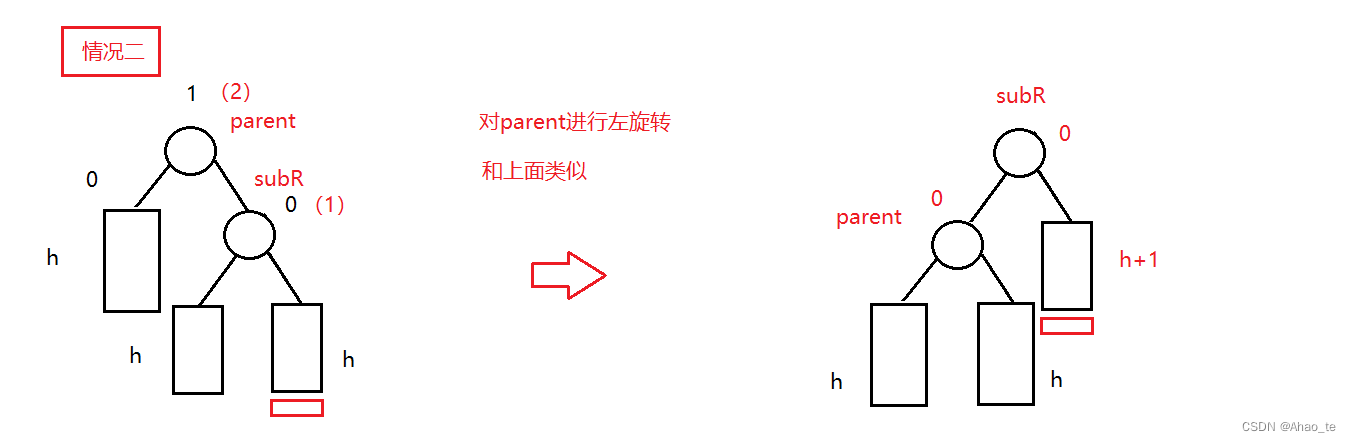
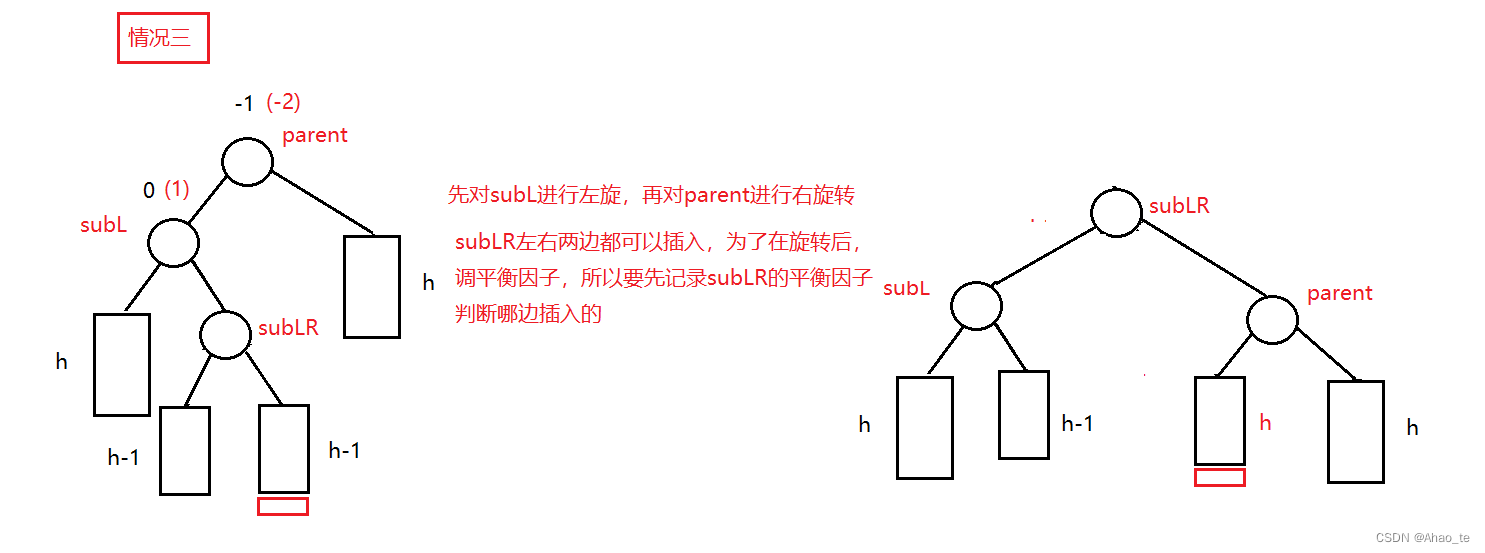
旋转有以下情况。
bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);//只能用kv值来确定parent和cur的指向if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//判断平衡因子while (parent){if (parent->_left == cur){//根节点左边插入节点,根的平衡因子-1parent->_bf--;}else{//根节点右边插入节点,根的平衡因子+1parent->_bf++;}//说明之前是-1或1,变为平衡if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){//下面子树高度差也影响了上面的根结点,所以需要向上调整cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//这个时候就需要旋转,使得树平衡if (parent->_bf == -2 && cur->_bf == -1){//这是右旋转的情况RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}//旋转完后,结构平衡,退出break;}else{//如果平衡因子出现其它情况,说明错了assert(false);}}//whilereturn true;}
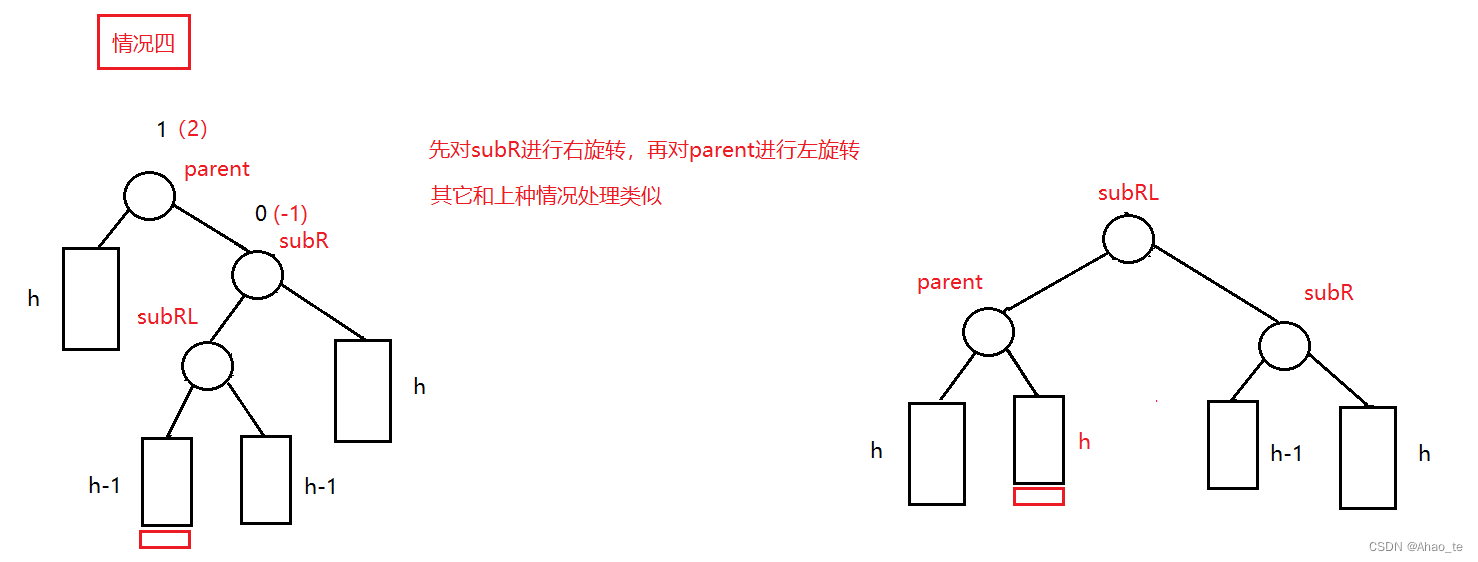
旋转:
//右旋转void RotateR(Node* parent){//从下到上依次修改Node* sub = parent->_left;Node* subR = sub->_right;//先改变最下面的subR结点parent->_left = subR;if (subR){subR->_parent = parent;}//再改变parent结点sub->_right = parent;Node* ppnode = parent->_parent;parent->_parent = sub;//最后改变sub结点if (ppnode == nullptr){_root = sub;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = sub;}else{ppnode->_right = sub;}sub->_parent = ppnode;}parent->_bf = sub->_bf = 0;}//左旋和右旋类似void RotateL(Node* parent){Node* sub = parent->_right;Node* subL = sub->_left;parent->_right = subL;if (subL){subL->_parent = parent;}sub->_left = parent;Node* ppnode = parent->_parent;parent->_parent = sub;if (ppnode == nullptr){_root = sub;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = sub;}else{ppnode->_right = sub;}sub->_parent = ppnode;}parent->_bf = sub->_bf = 0;}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;//保存subLR的平衡因子,为了知道从subLR哪边插入int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == -1) // subLR左子树新增{subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else if (bf == 1) // subLR右子树新增{parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (bf == 0) // subLR自己就是新增{parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}}//和上面类似void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == -1) // subRL左子树新增{subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 1) // subRL右子树新增{parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 0) // subRL自己就是新增{parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else{assert(false);}}
可能会有的问题解释(以下是自己的理解):
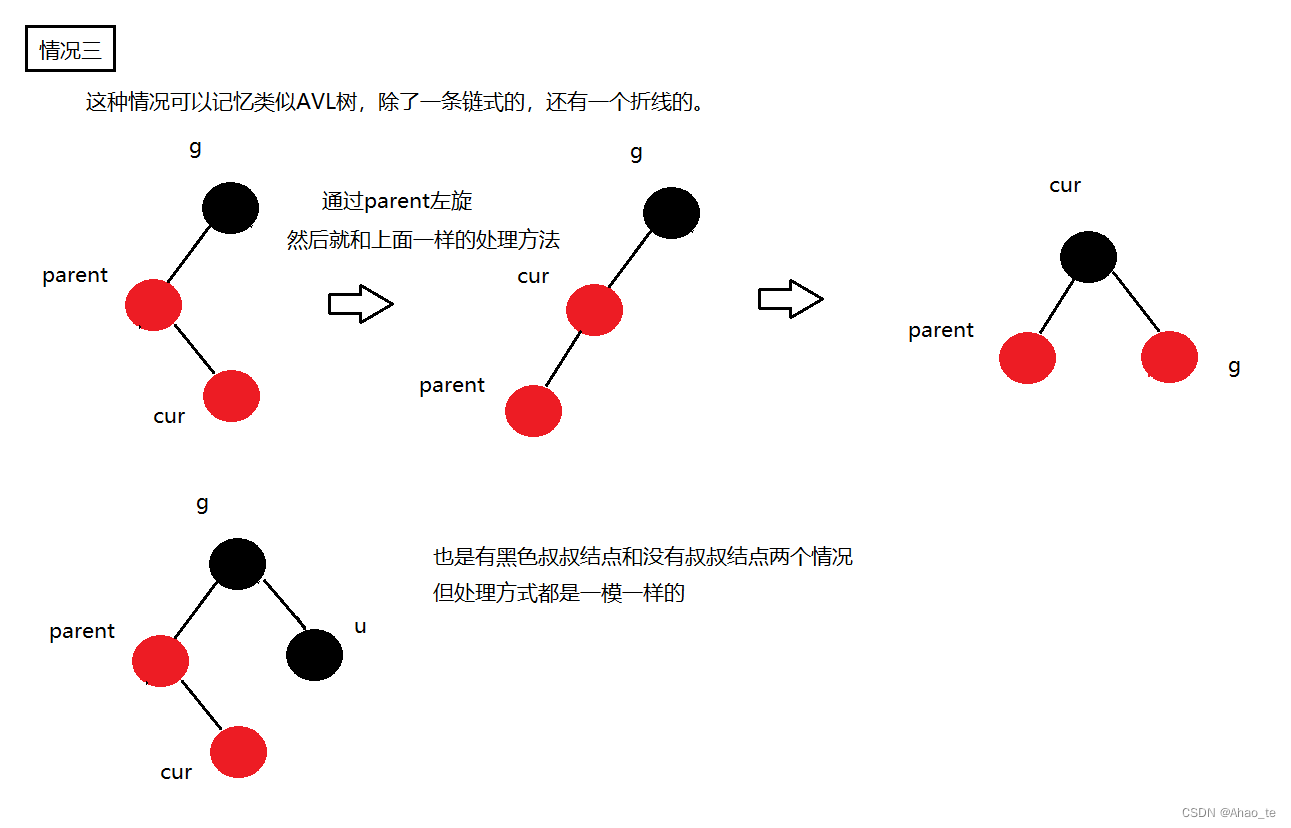
1、如何想到旋转的情况?
其实从所有情况看就这两个情况以及他们的翻转,记住它们两个就好了。
2、如何看左右旋?
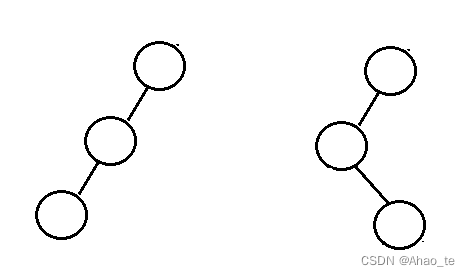
拿上图举例,左边是一个右旋能平衡的场景,只需要将最高的结点往右放就行。
右边是一个双选的场景,先将中间结点左旋,就成了图左边的场景,再右旋就行。
1.2 总结与测试AVL树
AVL树重点关注的是其平衡因子和选择如何使得AVL树平衡,通过插入了解就足够了。
下面是如何测试结果是AVL树:
1、通过每个结点的左右子树的高度判断平衡因子是否符合要求。
2、通过小和大的测试用例测试是不是AVL树
#pragma once
#include <iostream>
#include <assert.h>
using namespace std;template<class K, class V>
struct AVLTreeNode
{struct AVLTreeNode<K, V>* _left;struct AVLTreeNode<K, V>* _right;struct AVLTreeNode<K, V>* _parent;pair<K, V> _kv;int _bf;AVLTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool insert(const pair<K, V>& kv){}void RotateR(Node* parent){}void RotateL(Node* parent){}void RotateLR(Node* parent){}void RotateRL(Node* parent){}int Height(Node* root){if (root == nullptr){return 0;}int leftHight = Height(root->_left);int rightHight = Height(root->_right);return leftHight > rightHight ? leftHight + 1 : rightHight + 1;}bool IsBalanceTree(){return _IsBalanceTree(_root);}bool _IsBalanceTree(Node* parent){if (parent == nullptr){return true;}int leftHight = Height(parent->_left);int rightHight = Height(parent->_right);int diff = rightHight - leftHight;if (diff != parent->_bf || (diff > 1 || diff < -1)){cout << "有错" << endl;return false;}return _IsBalanceTree(parent->_left) && _IsBalanceTree(parent->_right);}void Inorder(){_Inorder(_root);}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}
private:Node* _root = nullptr;
};//出错用小用例调
void test1()
{int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };int arr2[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };AVLTree<int, int> t;for (auto& e : arr){if(e == 18){ //调试断点int a = 0;}t.insert(make_pair(e, e));t.IsBalanceTree();}t.Inorder();
}//没错用多数据看看能不能过
#include <cstdlib>
void test2()
{srand(time(NULL));AVLTree<int, int> t;for (int i = 0; i < 100000; ++i){int num = rand() % 10000;t.insert(make_pair(num, num));}t.IsBalanceTree();
}
2、红黑树
AVL树因为其严格的平衡导致它因为大量的旋转导致效率相较红黑树低。
红黑树不要求严格平衡,它为每个结点加上颜色区分,使得它趋向于平衡。它有着以下规定。
- 根节点必须是黑色。
- 根节点颜色要么是红色,要么是黑色。
- 红色结点不能连续。(也就是如果一个结点是红的,其两个子结点都是黑的)
- 每条路径下的黑色结点树要一样。
- 叶子结点都是黑色结点(这里叶子结点代表NULL结点)
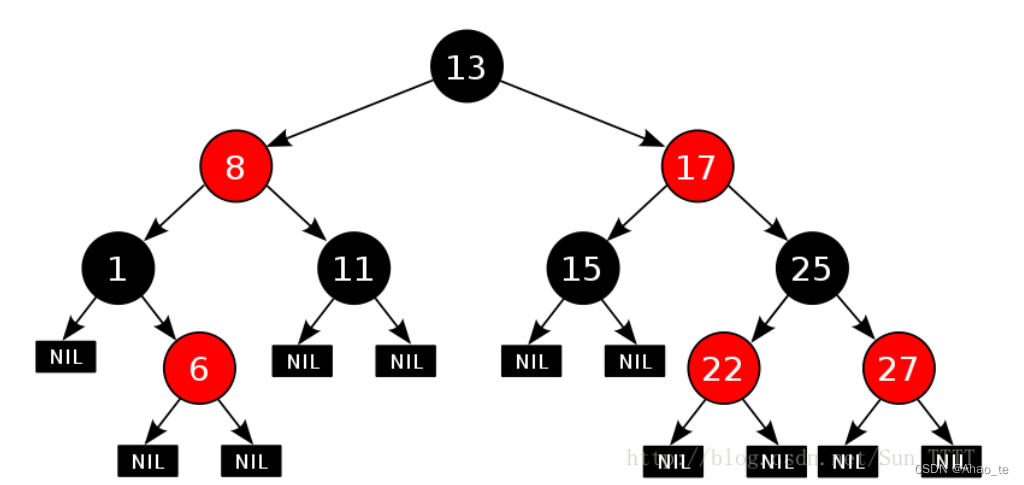
可能概念理解起来很抽象,我们通过代码一步步来。
首先搭建红黑树的框架。
大致和AVL树一样,只不过没有平衡因子,换成了颜色。
#include <iostream>
#include <assert.h>
using namespace std;enum Color { RED, BLACK };template<class K, class V>
struct RBTreeNode
{struct RBTreeNode<K, V>* _left;struct RBTreeNode<K, V>* _right;struct RBTreeNode<K, V>* _parent;pair<K, V> _kv;Color _col;RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(BLACK){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:
private:Node* _root = nullptr;
};
2.1 红黑树的插入
1、首先如果根是空,新建的结点一定是黑色结点。这很好理解。
2、那么如果是后面创建的结点,是黑色还是红色呢?
2.1 如果是黑色结点,那么想象一下,给某个路径添加一个黑色结点,使得这个路径的黑结点数量和其他路径不同,直接导致整个树不满足红黑树条件,直接破坏整个红黑树。
2.2 如果是红色结点,最差只会出现两个红色结点相连的情况,只影响这个子树。
所以综上选择影响最少的,选择创建红色结点。
3、插入前面和搜索树一样,得先确认插入的位置,以及和父节点链接。
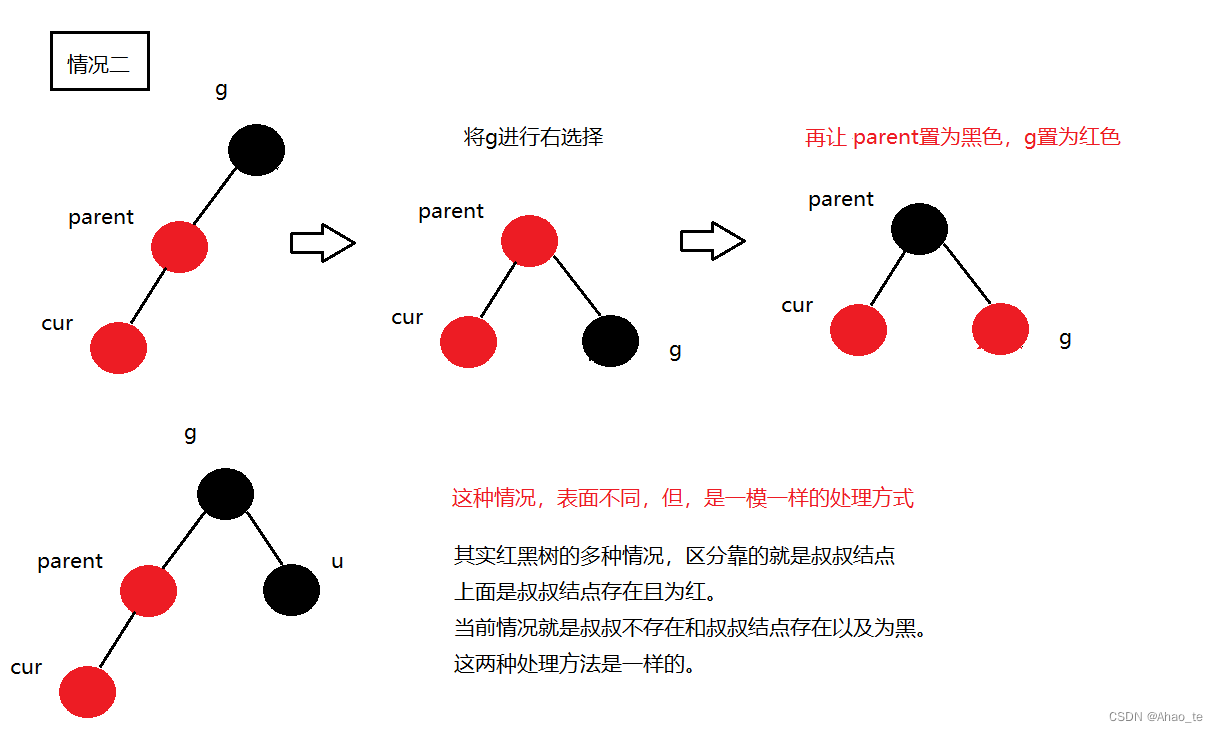
4、调整红黑树
除此以外当然还有翻转的另一类情况。
bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < cur->_kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//调整//parent为红,代表插入的子节点也为红,需要调整。while (parent && parent->_col == RED){Node* grandparent = parent->_parent;//首先是第一类父亲结点在祖父结点左边,叔叔结点在右边的一类情况。if (parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_col == RED){//第一种情况 叔叔结点存在且为红色parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;//向上调整,根节点的情况可以跑完整个调整,再设置_root->_col = BLACK;cur = grandparent;parent = cur->_parent;}else{//这一类是叔叔结点不存在以及存在为黑色//因为处理方法都是一样的,所以只要再区分直线型和折线型。if (parent->_right == cur){//折线的情况RotateL(parent);RotateR(grandparent);cur->_col = BLACK;grandparent->_col = RED;}else{//直线的情况RotateR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}break;}}else{//这一类是上面翻转,一样的处理,但注意方向Node* uncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}else{if (parent->_right == cur){RotateL(grandparent);parent->_col = BLACK;grandparent->_col = RED;}else{RotateR(parent);RotateL(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}}//最后确保根节点为黑。_root->_col = BLACK;return true;}//剩下左右旋转的代码和AVL中的一样。
如果记忆红黑树的情况?(个人方式)
首先要记得红黑树的特性,根一定是黑结点,想清楚为什么插入要插红结点,这样能更情况红黑树的特性。
像情况一的推理一样,先插入黑色的根节点,再插入红结点,层序插入直到出现问题,此时面对第一个情况,叔叔结点存在并且为红色。
然后考虑叔叔结点为黑和不存在的情况,因为要旋转,再根据AVL树中记忆的两个情况,推出除了直线型情况,还有折线型情况。
2.2 红黑树的测试
在测试中,需要判断的
1. 根要为黑结点。
2.判断父子结点不能都为红
3.确保每条路径的黑结点数相同(这里通过先计算一条路径的黑结点数,再和每一条路径比对)
bool Check(Node* proot, int count, int ref){if (proot == nullptr){//检查黑结点if (count != ref){cout << "出现路径黑结点树不同" << endl;return false;}return true;}Node* parent = proot->_parent;if (parent && (parent->_col == RED && proot->_col == RED)){cout << "出现了连续的红结点" << endl;return false;}if (proot->_col == BLACK){count += 1;}return Check(proot->_left, count, ref) && Check(proot->_right, count, ref);}bool IsRBTree(){if (_root == nullptr){return true;}if (RED == _root->_col){cout << "根节点不能为红色" << endl;return false;}int ref = 0;Node* checkblack = _root;while (checkblack){if (BLACK == checkblack->_col){ref++;}checkblack = checkblack->_left;}return Check(_root, 0, ref);}
本节完~
相关文章:
【C++】AVL树和红黑树(插入和测试详解)
文章目录1、AVL树1.1 AVL树的插入1.2 总结与测试AVL树2、红黑树2.1 红黑树的插入2.2 红黑树的测试了解AVL树是为了了解红黑树,了解红黑树是为了更好的理解set和map。 1、AVL树 AVL树是在二叉搜索树的基础上进行了严格的平衡,能做到平衡的关键是通过平衡…...

Centos7 安装 Mysql 8.0.32,详细完整教程(好文章!!)
mysql5.7的安装方式参考之前的文章: centos7 安装 Mysql 5.7.27,详细完整教程(好文章!!)_HD243608836的博客-CSDN博客 一、检查mysql版本冲突 先检查是否已经存在mysql,若存在卸载࿰…...
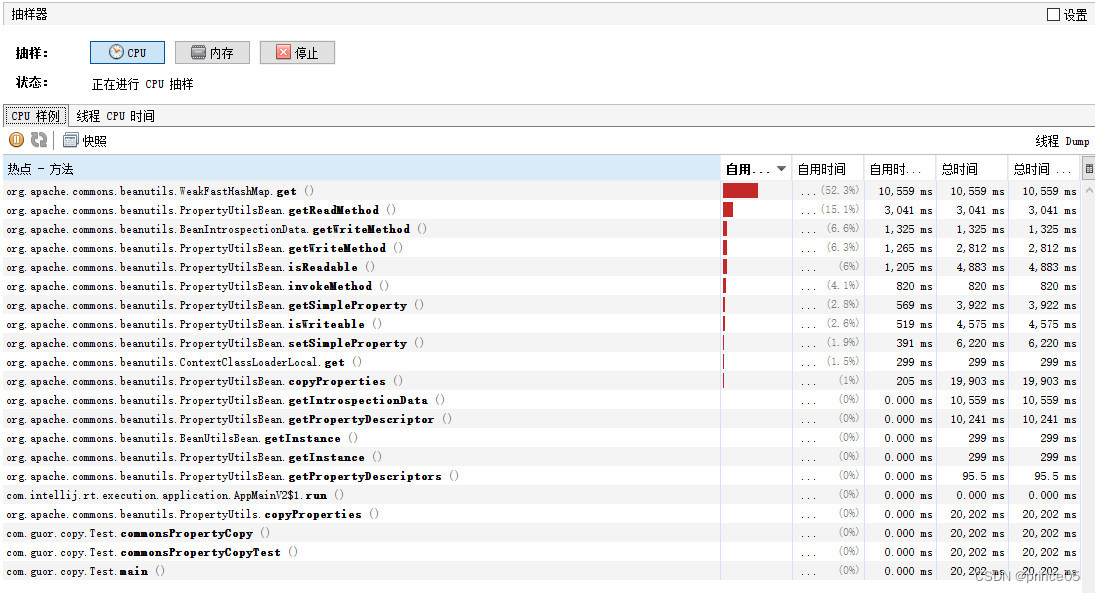
Apache Beanutils为什么被禁止使用?
收录于热门专栏Java基础教程系列(进阶篇) 在实际的项目开发中,对象间赋值普遍存在,随着双十一、秒杀等电商过程愈加复杂,数据量也在不断攀升,效率问题,浮出水面。 问:如果是你来写…...
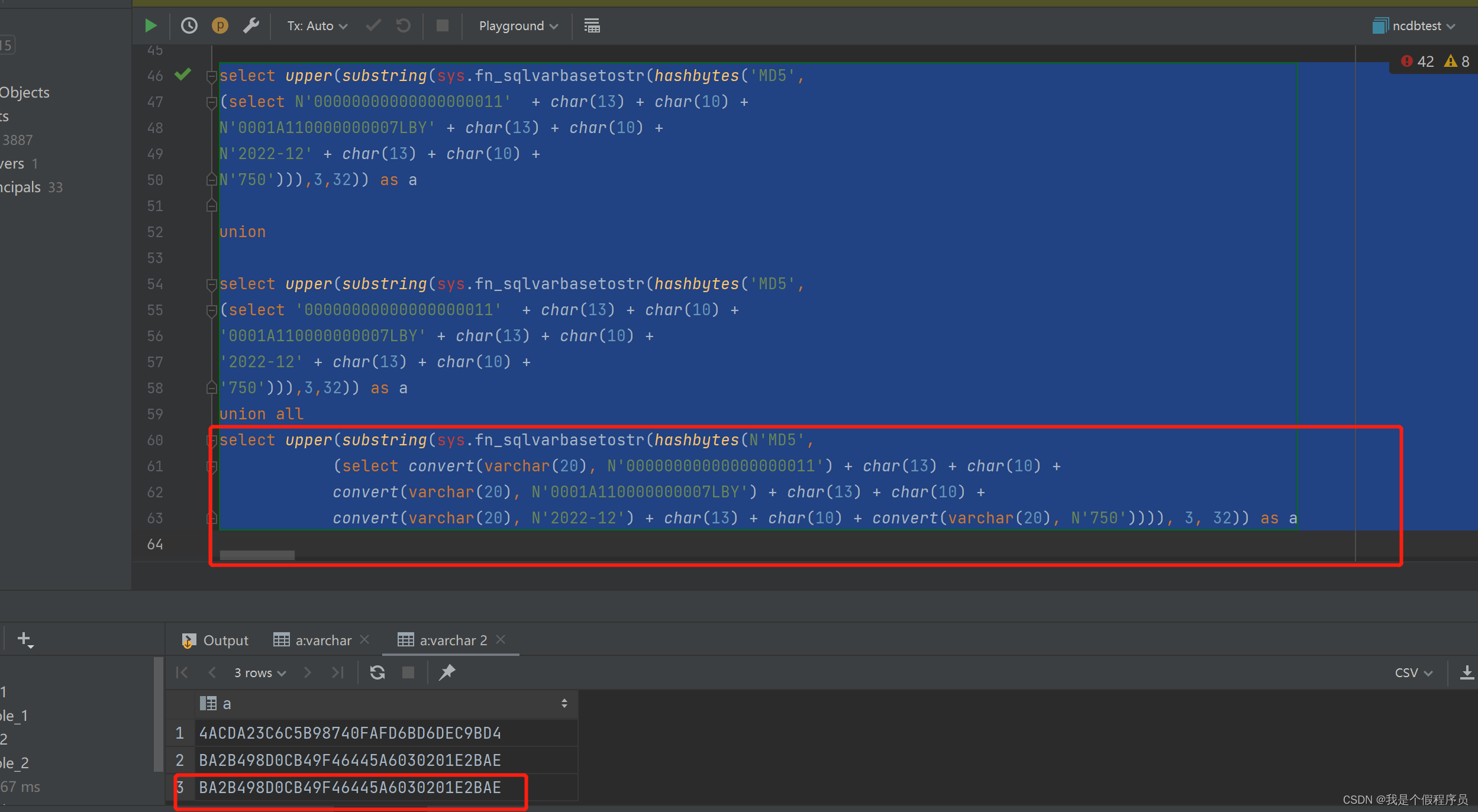
sql server执行md5加密的时候,字符串前带N和不带N的结果是不一样的
最近因为项目的需要,报表中需要对数据进行MD5加密,结果报表系统得出来的sql语句,字符串前都自动带了N,执行时,发现得到的结果跟在数据库中执行的sql(字符串不带N)得的值不一样,最后自…...

01Python编译器和编辑器下载
Python下载 通过python官网下载:https://www.python.org/因为python官网的服务器在国外,我们可以通过腾讯软件中心下载https://pc.qq.com/search.html#!keyword=python 腾讯软件中心下载请使用普通下载,其他什么下载会自动帮你下个电脑管家(没必要) python简单描述 python…...

CHAPTER 5 自动发现、自动注册、分布式监控、SNMP监控
自动发现与自动注册5.1 自动发现与自动注册5.1.1 简介5.1.2 两种模式5.2 自动发现--被动模式5.3 自动注册--主动模式5.4 分布式监控5.4.1 介绍5.4.2 配置zabbix proxy5.5 SNMP监控5.5.1 使用范围5.5.2 安装snmp程序5.5.3 配置snmp程序5.5.4 测试snmp5.5.5 在web界面进行配置5.1…...

P5311 [Ynoi2011] 成都七中
题目描述 给你一棵 nnn 个节点的树,每个节点有一种颜色,有 mmm 次查询操作。 查询操作给定参数 lrxl\ r\ xl r x,需输出: 将树中编号在 [l,r][l,r][l,r] 内的所有节点保留,xxx 所在连通块中颜色种类数。 每次查询操…...

Python 日期和时间格式
Python 程序能用很多方式处理日期和时间,转换日期格式是一个常见的功能。Python 提供了一个 time 和 calendar 模块可以用于格式化日期和时间。时间间隔是以秒为单位的浮点小数。每个时间戳都以自从1970年1月1日午夜(历元)经过了多长时间来表…...

电脑和手机的软件推荐
安卓软件 jota text 记事本 x浏览器 (支持禁js,支持嗅探 视频 音频) __ 空缺 暂未能发现好用的office软件 snapseed图片调整 可谓手机界的photoshop vidtrim视频剪辑 librera reader (无广告 电子书软件 但是发音很差 lithum或者…...
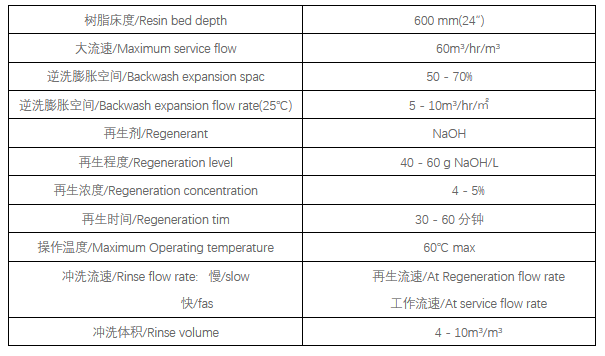
酸回收树脂的应用
酸洗废水 在轧钢、金属表面处理、电子元件制造等过程中需要清除钢材表面氧化铁皮而使用酸进行酸洗,酸洗过程中会产生废酸液和酸洗废水。 这些废酸产量大、酸度高,而且由于酸洗废水来自钢铁和金属表面处理的清洗水,水中含有多种重金属离子&am…...
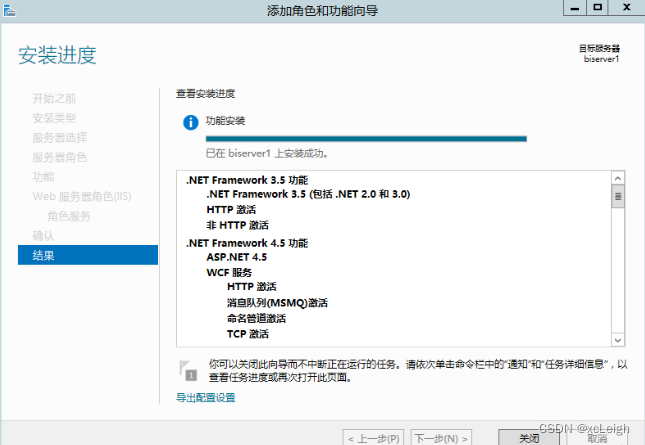
windows上配置IIS全过程
文章目录1️⃣ 配置IIS1.1 从开始打开服务器管理1.2 添加角色和功能1.3 添加角色和功能向导1.4 按照如下步骤选择2️⃣ 问题:缺少源文件解决方案优质资源分享作者:xcLeigh 文章地址:https://blog.csdn.net/weixin_43151418/article/details/1…...

软考高级信息系统项目管理师系列之十三:项目成本管理
软考高级信息系统项目管理师系列之十三:项目成本管理 一、成本管理领域输入、输出、工具和技术表二、成本管理基础知识点1.成本类型2.应急储备和管理储备3.成本基准三、项目成本管理过程1.项目成本管理的过程2.成本管理计划3.项目成本估算的主要步骤4.活动成本估算5.项目预算6…...
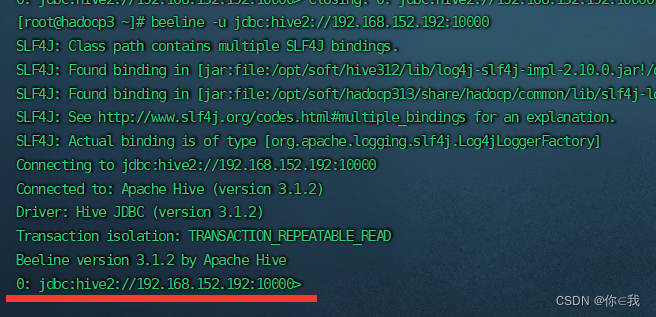
HIVE 基础(一)
目录 启动hive 方式一 方式二 修改hdfs上给定文件执行的读写权限 创建数据库 查看数据库 查看数据库详细信息 查看当前数据库 创建表 查看建表语句 查看表信息 删除表 添加数据 查看表数据 删除数据库 强制删除数据库 启动hive 方式一 [roothadoop1 ~]# hive 方…...

《狂飙》壁纸太帅,Python自动切换太酷(8)
小朋友们好,大朋友们好!我是猫妹!要说最近什么电视剧最火?非《狂飙》莫属。《狂飙》剧名来自毛主席诗词“国际悲歌歌一曲,狂飙为我从天落”。导演借用“狂飙”二字来比喻剧中的扫黑除恶大风暴。据了解,《狂…...

博客排名的影响是什么? 说明优点、注册方法和推荐网站
如果您经营博客,您是否在博客排名网站上注册?博客排名网站是以排名格式介绍各种注册博客的网站。如果您注册博客,您将有更多机会被人们看到,并且可以期望增加访问权限。对于那些刚刚打开博客并担心访问量不会轻易增加的人来说&…...
全流程GMS地下水数值模拟技能培养及溶质运移反应问题深度解析实践技术
本次综合前期多次学习的效果及重点关注环节,系统性呈现地下水数值模拟软件GMS建模方法同时,建立与实践项目过程中的重点问题相融合,在教学中不仅强调学习三维地质结构建模、水文地质模型概化、边界条件设定、参数反演和模型校核等关键环节&am…...
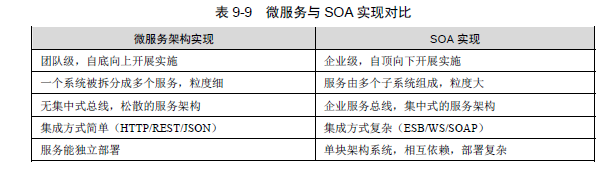
【软件架构设计】SOA/软件架构设计---面向服务的架构(SOA详细解释)
文章目录面向服务的架构SOA 概述1. 服务的基本结构2.SOA 设计原则3. 服务构件与传统构件SOA 的关键技术1. UDDI2.WSDL3.SOAP4.RESTSOA 的实现方法1.Web Service2. 服务注册表3. 企业服务总线微服务1.微服务的优势2. 微服务面临的挑战3.微服务与 SOA面向服务的架构 迄今为止&am…...

erupt框架Ueditor富文本编辑器图片上传出现405异常
最近在研究erupt框架(v1.11.2),当字段使用Ueditor富文本编辑器,在图片上传的时候出现405异常,接口不支持POST请求方式: 根据错误提示找到对应的源码,发现Handler方法只支持GET请求,而图片上传的时候是以POST方式发起请求的; 此时需要修改源码,用自定义的类覆盖jar包中同名的…...

FILE文件操作
文件指针 每个被使用的文件都在内存中开辟了一个相应的文件信息区,用来存放文件的相关信息(如文件的名 字,文件状态及文件当前的位置等)。这些信息是保存在一个结构体变量中的。该结构体类型是有系统 声明的,取名FILE…...

SAP PP工单确认完成(CNF)状态取消方法
这SAP PP工单确认完成(CNF)状态取消方法SAP PP工单确认完成(CNF)状态取消方法SAP PP工单确认完成(CNF)状态取消方法 工单完工后取消了其中的一个报工,然后无法再报工 此时再报工,系…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...

【Pandas】pandas DataFrame dropna
Pandas2.2 DataFrame Missing data handling 方法描述DataFrame.fillna([value, method, axis, …])用于填充 DataFrame 中的缺失值(NaN)DataFrame.backfill(*[, axis, inplace, …])用于**使用后向填充(即“下一个有效观测值”)…...

C++参数传递 a与a的区别
在 C 中,&a(引用)和 a(值传递) 的关键区别在于 参数如何传递给函数,以及由此引发的 性能、语义和安全问题。 最核心的在于你想不想传入的参数被改变,如果想,就用参数传递&#…...

鸿蒙APP测试实战:从HDC命令到专项测试
普通APP的测试与鸿蒙APP的测试有一些共同的特征,但是也有一些区别,其中共同特征是,它们都可以通过cmd的命令提示符工具来进行app的性能测试。 其中区别主要是,对于稳定性测试的命令的区别,性能指标获取方式的命令的区…...

React 进阶特性
1. ref ref 是 React 提供的一种机制,用于访问和操作 DOM 元素或 React 组件的实例。它可以用于获取某个 DOM 元素的引用,从而执行一些需要直接操作 DOM 的任务,例如手动设置焦点、选择文本或触发动画。 1.1. 使用 ref 的步骤 1. 创建一个 ref:使用 React.createRef 或 …...