质数(判定质数 分解质因数 筛质数)
目录
- 一、判定质数
- 思路分析
- 代码实现
- 二、分解质因数
- 思路分析
- 典型题目
- 代码实现
- 三、质数筛
- 经典题目
- 思路分析
- 1. 朴素筛法
- 2. 埃氏筛法
- 3. 欧拉筛法
一、判定质数
思路分析
由于每个合数的因子是成对出现的,即如果 d d d 是 n n n 的因子,那么 n d \frac{n}{d} dn 也是 n n n 的因子,故从 1 1 1 到 n n n 的枚举可以缩减到 1 1 1 到 n \sqrt{n} n,即让 d ≤ n d d \leq \frac{n}{d} d≤dn,从而得到 d ≤ n d \leq \sqrt{n} d≤n。
代码实现
bool is_prime(int n)
{if (n < 2) return false;for (int i = 2; i <= n / i; ++i){if (n % i == 0) return false;}return true;
}
时间复杂度: O ( n ) O(\sqrt{n}) O(n)
二、分解质因数
思路分析
每个合数都是由质数相乘得到的。合数可以写成质因数的乘积,这是数论中的一个基本命题。
例如:
12 = 2 * 2 * 3
18 = 2 * 3 * 3
24 = 2 * 2 * 2 * 3
① 对于任何一个合数 n n n,在它的质因数分解中,至多有一个质因子大于 n \sqrt{n} n。
② 同时也可以推出,对任何一个合数 n n n,在它的质因数分解中,至少会有一个质因子小于或等于 n \sqrt{n} n。
典型题目
题目描述:
给定 n n n 个正整数 a i a_i ai,将每个数分解质因数,并按照质因数从小到大的顺序输出每个质因数的底数和指数。
输入格式:
第一行包含整数 n n n。
接下来 n n n 行,每行包含一个正整数 a i a_i ai。
输出格式:
对于每个正整数 a i a_i ai,按照从小到大的顺序输出其分解质因数后,每个质因数的底数和指数,每个底数和指数占一行。
每个正整数的质因数全部输出完毕后,输出一个空行。
数据范围:
1 ≤ n ≤ 100 , 2 ≤ a i ≤ 2 ∗ 1 0 9 1≤n≤100,2≤a_i≤2*10^9 1≤n≤100,2≤ai≤2∗109
输入样例:
2
6
8
输出样例:
2 1
3 12 3
代码实现
#define _CRT_NO_SECURE_WARNINGS
#include<iostream>using namespace std;void divide(int x)
{for (int i = 2; i <= x / i; ++i) // 遍历出所有小于或等于sqrt(n)的质因子{if (x % i == 0){int cnt = 0;while (x % i == 0){cnt++;x /= i;}cout << i << ' ' << cnt << endl;}}// 输出大于sqrt(n)的质因子或是质数本身if (x > 1) cout << x << ' ' << 1 << endl;cout << endl;
}
int main()
{int n;cin >> n;while (n--){int x;cin >> x;divide(x);}return 0;
}
时间复杂度:在 O ( log n ) O(\log n) O(logn) 与 O ( n ) O(\sqrt n) O(n)之间
解释:若 n n n 为 2 2 2 的倍数,时间复杂度将会变为 O ( log n ) O(\log n) O(logn)。
三、质数筛
经典题目
题目描述:
给定一个正整数 n n n,请你求出 1 ∼ n 1∼n 1∼n 中质数的个数。
输入格式:
共一行,包含整数 n n n。
输出格式:
共一行,包含一个整数,表示 1 ∼ n 1∼n 1∼n 中质数的个数。
数据范围:
1 ≤ n ≤ 1 0 6 1≤n≤10^6 1≤n≤106
输入样例:
8
输出样例:
4
思路分析

通过将素数的倍数筛掉的方法,剩余存留的则全为质数。
筛完后 P P P 与 2 2 2 ~ ( P − 1 P-1 P−1) 之间不存在倍数关系,即 P P P 无质因子在 2 2 2 ~ ( P − 1 P-1 P−1) 之间。
1. 朴素筛法
通过将2~n的所有数的倍数筛掉的方法来得到范围内所有的质数
#define _CRT_NO_SECURE_WARNINGS
#include<iostream>using namespace std;const int N = 1e6 + 10;
int prime[N], cnt;
bool st[N];void get_prime(int n)
{for (int i = 2; i <= n; ++i){if (!st[i]){prime[cnt++] = i;}for (int j = 2 * i; j <= n; j += i) st[j] = true; // 将2~n所有数的倍数都打上标记}
}
int main()
{int n;cin >> n;get_prime(n);cout << cnt << endl;return 0;
}
时间复杂度: O ( n log n ) O(n \log n) O(nlogn)
n 2 + n 3 + n 4 + . . . + + n n = n ( 1 2 + 1 3 + 1 4 + . . . + 1 n ) \frac{n}{2} + \frac{n}{3} + \frac{n}{4} + ... + + \frac{n}{n} = n(\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{n}) 2n+3n+4n+...++nn=n(21+31+41+...+n1)
调和级数: lim n → ∞ ( 1 2 + 1 3 + 1 4 + . . . + 1 n ) = ln n + c \lim_{n \to \infty} (\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{n}) = \ln n + c limn→∞(21+31+41+...+n1)=lnn+c (欧拉常数 c = 0.577 c = 0.577 c=0.577)
因此可得时间复杂度为 O ( n log n ) O(n \log n) O(nlogn)
2. 埃氏筛法
优化了朴素筛法,只将2~n的质数的倍数筛掉的方法来得到范围内所有的质数
#define _CRT_NO_SECURE_WARNINGS
#include<iostream>using namespace std;const int N = 1e6 + 10;
int prime[N], cnt;
bool st[N];void get_prime(int n)
{for (int i = 2; i <= n; ++i){if (st[i]) continue;prime[cnt++] = i;for (int j = 2 * i; j <= n; j += i) st[j] = true; // 将2~n所有质数的倍数都打上标记}
}
int main()
{int n;cin >> n;get_prime(n);cout << cnt << endl;return 0;
}
时间复杂度为 O ( n log log n ) O(n \log \log n) O(nloglogn)
质数定理:在 1 1 1 到 n n n 之间的质数个数约等于 n ln n \frac{n}{\ln n} lnnn
3. 欧拉筛法
核心思想:在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。
步骤:
- 从 i = 2 i = 2 i=2 开始,如果 i i i 还没有被筛掉,则将 i i i 加入至素数列表中。
- 遍历当前素数列表 p r i m e [ ] prime[] prime[],筛去 i ∗ p r i m e [ j ] i ∗ prime[j] i∗prime[j]。
(保证 p r i m e [ j ] ∗ i prime[j] ∗ i prime[j]∗i 不能越界,因为越界了对结果没意义。即 i ∗ p r i m e [ j ] ≤ n i ∗ prime[j] \leq n i∗prime[j]≤n) - 当遍历到能整除 i 的素数 p r i m e [ j ] prime[j] prime[j] 时,筛去 i ∗ p r i m e [ j ] i ∗ prime[j] i∗prime[j],停止对素数列表的遍历。
- 重复 2 , 3 , 4 2,3,4 2,3,4,直到所有不超过 n n n 的整数都被遍历过素数列表中的元素即为所求的不超过 n n n 的所有素数。
#define _CRT_NO_SECURE_WARNINGS
#include<iostream>using namespace std;const int N = 1e6 + 10;
int cnt, prime[N];
bool st[N];void get_prime(int n)
{for (int i = 2; i <= n; ++i){if (!st[i]) prime[cnt++] = i;for (int j = 0; prime[j] <= n / i; j++){st[prime[j] * i] = true;if (i % prime[j] == 0) break; // 只被它的最小质因子筛选一次}}
}
int main()
{int n;cin >> n;get_prime(n);cout << cnt << endl;return 0;
}
若 n < 1 0 6 n<10^6 n<106,欧拉筛和埃氏筛所花费的时间差不多;但是若 n > 1 0 7 n>10^7 n>107,欧拉筛会比埃氏筛快了大概一倍。
相关文章:

质数(判定质数 分解质因数 筛质数)
目录 一、判定质数思路分析代码实现 二、分解质因数思路分析典型题目代码实现 三、质数筛经典题目思路分析1. 朴素筛法2. 埃氏筛法3. 欧拉筛法 一、判定质数 思路分析 由于每个合数的因子是成对出现的,即如果 d d d 是 n n n 的因子,那么 n d \frac…...
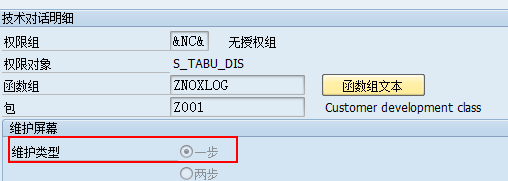
SAP数据库表维护视图生成器的使用
在SAP中,经常需要自定义数据库表。而且可能需要人工维护数据库表中的数据,可以通过SM30进行维护数据;但是SM30事务的权限太大,不适宜将SM30直接分配;因此,可以通过给维护表分配事务代码,来达到控…...
数据结构 | 递归
目录 一、何谓递归 1.1 计算一列数之和 1.2 递归三原则 1.3 将整数转换成任意进制的字符串 二、栈帧:实现递归 三、递归可视化 四、谢尔平斯基三角形 五、复杂的递归问题 六、动态规划 一、何谓递归 递归是解决问题的一种办法,它将问题不断地分…...

微信发视频怎么不压缩画质?试试这几招
微信是我们常用的社交工具了,很多朋友都会用它跟好友分享视频,但想必大家都知道,微信为了节省宽带和存储空间,会自动对上传的视频进行压缩处理,甚至过大的视频会被限制发送,怎么才能让微信不自动压缩画质呢…...
【网络安全带你练爬虫-100练】第16练:使用session发送请求
目录 一、目标1:使用seesion进去请求 二、网络安全O 一、目标1:使用seesion进去请求 (1)应用: 通过创建会话(session)对象来请求并爬取返回的数据包 情景:需要登录才能爬取的网…...

论文代码学习—HiFi-GAN(3)——模型损失函数loss解析
文章目录 引言正文生成器损失函数最小二乘损失函数梅尔频谱图损失函数特征匹配损失函数生成器最终损失函数loss生成器loss对应代码 鉴定器损失函数鉴定器损失函数代码 总结引用 引言 这里翻译了HiFi-GAN这篇论文的具体内容,具体链接。这篇文章还是学到了很多东西&a…...
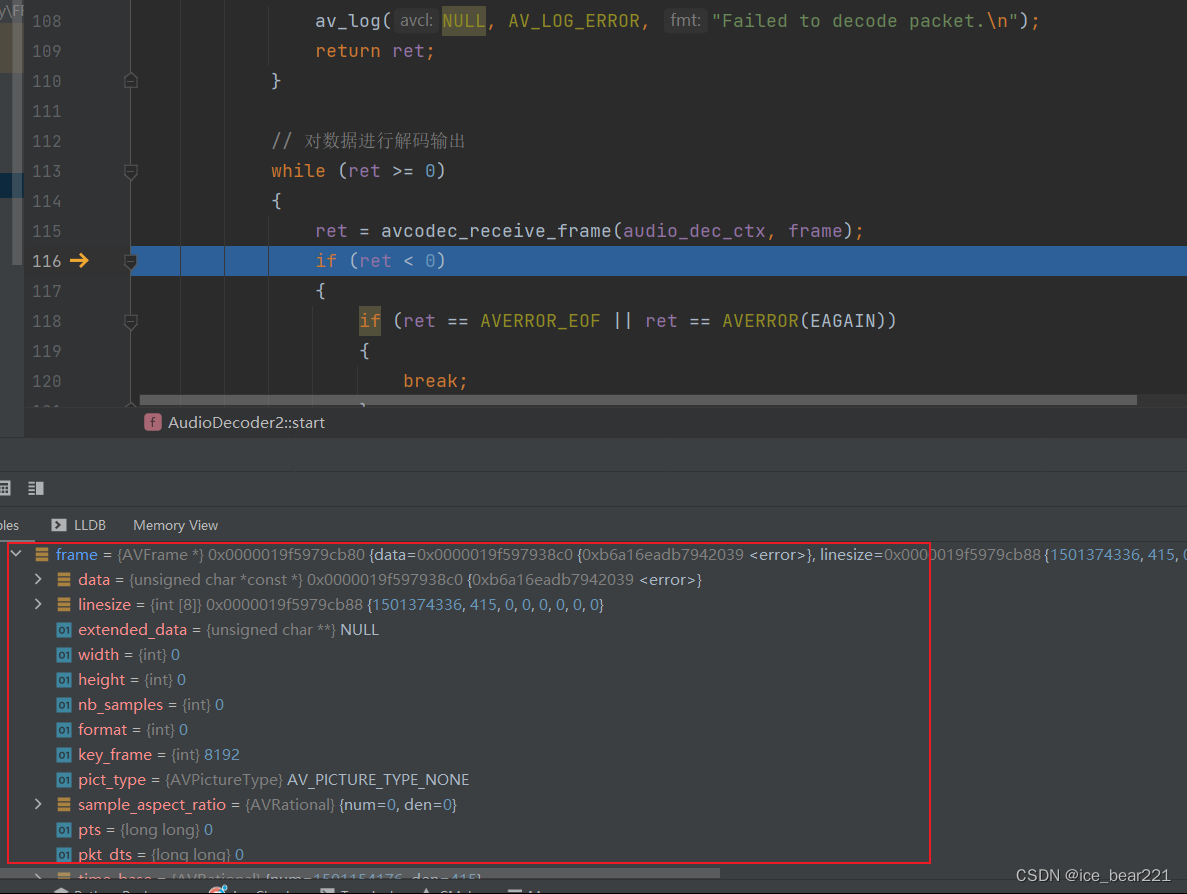
CLion中avcodec_receive_frame()问题
1. 介绍 在提取音视频文件中音频的PCM数据时,使用avcodec_receive_frame()函数进行解码时,遇到了一些问题,代码在Visual Studio 2022中运行结果符合预期,但是在CLion中运行时,获取的AVFrame有错误,和VS中获…...
Linux安装操作(Mac版本)
Parallels Desktop的简介 Parallels Desktop是Mac平台上的虚拟机软件,也是Mac平台最好的虚拟机软件之一。它允许用户在Mac OS X系统上同时运行其他操作系统,例如Windows、Linux等。Parallels Desktop为Mac用户提供了使用其他操作系统和软件的便利性&…...
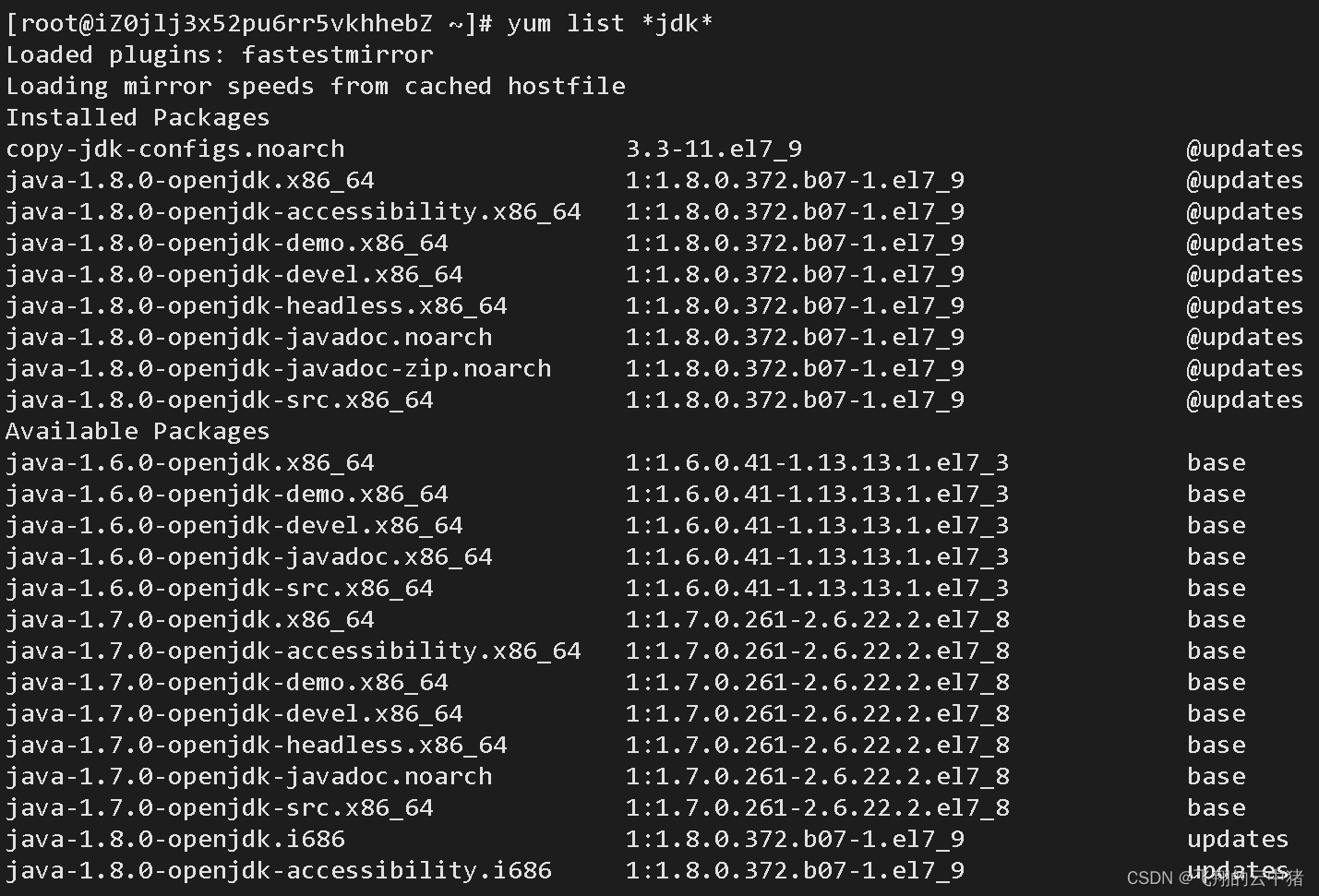
Linux(四)--包软件管理器与Linux上软件的下载示例
一.包软件管理器【yum和apt】 1.先来学习使用yum命令。yum:RPM包软件管理器,用于自动化安装配置Linux软件,并可以自动解决依赖问题。通过yum命令我们可以轻松实现软件的下载,查找,卸载与更新等管理软件的操作。 最常用…...

HTML <param> 标签
实例 向 HTML 代码添加一个对象: <object classid="clsid:F08DF954-8592-11D1-B16A-00C0F0283628" id="Slider1" width="100" height="50"><param name="BorderStyle" value="1" /><param nam…...
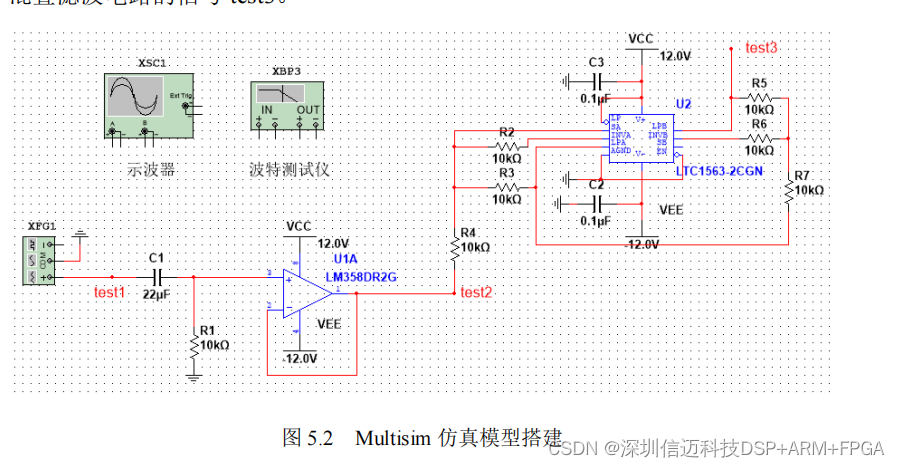
基于ARM+FPGA (STM32+ Cyclone 4)的滚动轴承状态监测系统
状态监测系统能够在故障早期及时发现机械设备的异常状态,避免故障的 进一步恶化造成不必要的损失,滚动轴承是机械设备的易损部件,本文对以滚动 轴承为研究对象的状态监测系统展开研究。现有的监测技术多采用定时上传监 测数据,…...

二、数据结构10:堆 模板题+算法模板(堆排序,模拟堆)
文章目录 算法模板堆题目代码模板堆的原理down操作理解:up操作理解建堆操作关于heap_swap中存的映射数组理解(模拟堆题目中用到) 模板题堆排序原题链接题目思路题解 模拟堆原题链接题目思路题解 算法模板 堆题目代码模板 // h[N]存储堆中的…...
W6100-EVB-PICO做DNS Client进行域名解析
前言 在上一章节中我们用W6100-EVB-PICO通过dhcp获取ip地址(网关,子网掩码,dns服务器)等信息,给我们的开发板配置网络信息,成功的接入网络中,那么本章将教大家如何让我们的开发板进行DNS域名解…...

【linux-网络】4层转发方法-iptable以及nginx
1.背景 有时候远程或者某些业务需要做转发就会用到iptables或者nginx,或者ss都可以 根据自己的情况去适配。 2.方法: 1)iptables -把linux内核转发功能打开 echo "net.ipv4.ip_forward1" >> /etc/sysctl.conf -出入转发…...

vue复制文案,复制图片,黏贴图片
vue 实现复制文案,复制图片,在微信聊天框,黏贴为图片 //安装 cnpm i clipboard-all //引用 import clipboard from clipboard-all<!-- row.url 图片路径 --><div ref"foo" class"hidden"><img :src"…...

Web应急思路
Web应急思路 找到webshell --> 确定攻击者IP --> 回溯攻击者操作 --> 梳理整个攻击过程 1.寻找webshell方法 1.文件内容中的恶意函数 2.web日志中的webshell特征 3.贴合web业务中的URL来分析web日志 4.源码版本管理对比,注重修改或新增的脚本文件 5.统计…...
shell脚本清理redis模糊匹配的多个key,并计算释放内存大小
#!/bin/bash# 定义Redis服务器地址和端口 REDIS_HOST"localhost" REDIS_PORT6380# 获取Redis当前内存使用量(以字节为单位) function get_redis_memory_usage() {redis-cli -h $REDIS_HOST -p $REDIS_PORT INFO memory | grep "used_memo…...

python-MySQL数据库建表语句(需要连接数据库)转存为Excel文档-工作小记
将create table XXXXXX 转为指定Excel文档。该脚本适用于数据库表结构本地文档记录 呈现效果 代码 # -*- coding:utf-8 -*- # Time : 2023/8/2 15:14 # Author: 水兵没月 # File : MySQL建表_2_excel.py import reimport mysql.connector import pandas as pd db 库名 mydb …...

iOS Block介绍
文章目录 一、Block定义二、block为什么用copy修饰三、block使用时的注意事项四、使用 block时什么情况会发生引用循环,如何解决?五、在block内如何修改block外部变量?六、__block与__weak的区别 一、Block定义 目的就是能够直接存储一个代码…...

小程序安全性加固:如何保护用户数据和防止恶意攻击
第一章:引言 在当今数字化时代,移动应用程序的使用已经成为人们日常生活中的重要组成部分。小程序作为一种轻量级的应用程序形式,受到了广泛的欢迎。然而,随着小程序的流行,安全性问题也日益凸显。用户数据泄露和恶意攻…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
