【使用 DSP 滤波器加速速度和位移】使用信号处理算法过滤加速度数据并将其转换为速度和位移研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
对于实时采集的加速度数据,可以应用信号处理算法,如数字滤波和积分运算,将其转换为速度和位移数据。下面是一个简要的概述:
1. 数据采集:首先需要进行数据采集,通过传感器获取物体的加速度数据。这可以通过加速度计等传感器来实现,例如使用微电机惯性测量单元(IMU)或加速度传感器。
2. 数字滤波:为了去除噪声和不必要的高频分量,可以应用数字滤波技术,如低通滤波器。常见的滤波器类型包括巴特沃斯滤波器、无限脉冲响应(IIR)滤波器和有限脉冲响应(FIR)滤波器。滤波后的信号将更加平滑和稳定。
3. 数值积分:将经过滤波的加速度信号积分一次,可以得到速度信号。数值积分是通过近似求解离散点间的微分来实现的。积分操作会导致积分误差的累积,因此需要考虑误差修正和积分漂移校准的方法。
4. 二次积分:将经过滤波和积分的速度信号再次积分,可以得到位移信号。同样,二次积分也会引入积分误差的累积,因此需要对误差进行校正和修正。
5. 校准和校正:为了获得准确的结果,可能需要进行传感器的校准和校正。这包括零偏校准、灵敏度校准和加速度计的温度效应校正等。
需要注意的是,将加速度数据转换为速度和位移的过程是一个近似计算,其中存在积分误差的累积,尤其是在长时间的测量中。因此,在进行精确位移测量时,需要考虑积分误差的校准和修正。
总结来说,将加速度数据转换为速度和位移的过程包括数据采集、数字滤波、数值积分和二次积分。每个步骤都需要选择合适的算法和参数,并进行校准和修正,以获得准确可靠的速度和位移结果。
📚2 运行结果
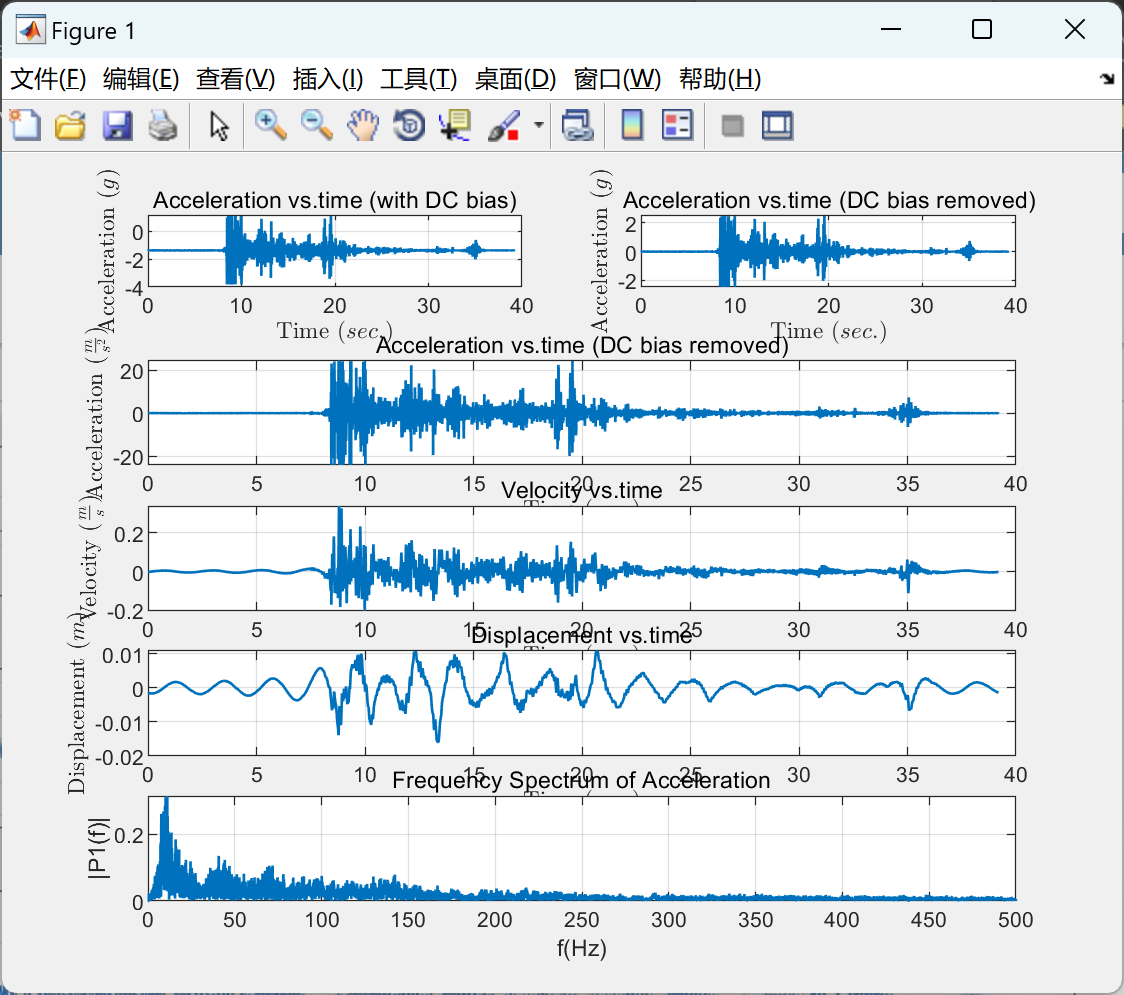

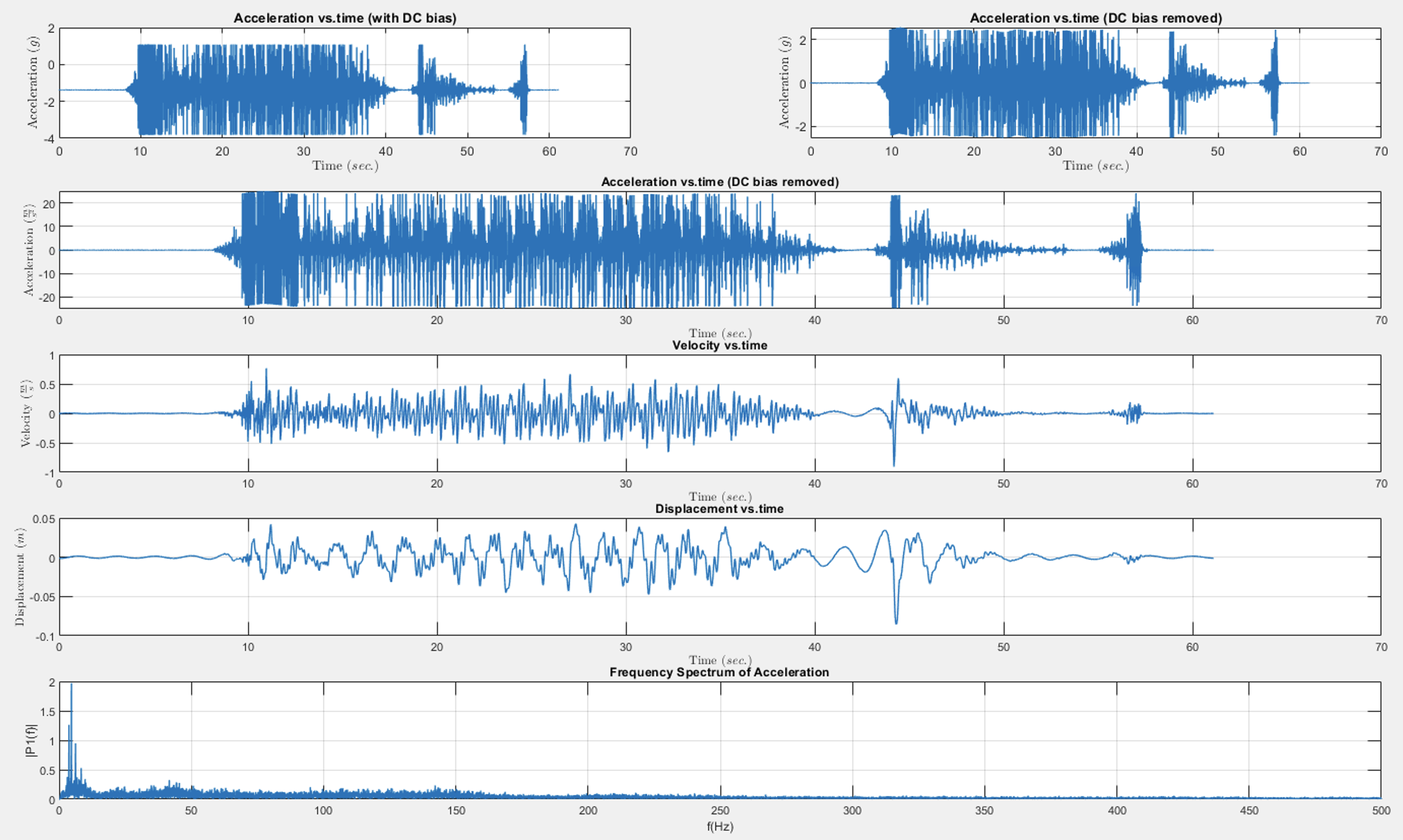
部分代码:
%% Processed inputs
%--------------------------------------------------------------------------
time = data(:,1); % Time vector
accval_g = data(:,2); % Acceleration in g
accval = data(:,2)*9.81; % Acceleration in m/s^2
L = size(data,1); % Length of signal
Fs = 1/(time(2)-time(1)); % Sampling frequency
Ts = 1/Fs; % Sampling period
%% Displacement, Velocity and Acceleration
%--------------------------------------------------------------------------
[~, ~, ~, filtered_acc_g] ...
= accelo2disp(time,Ts, Fs, Fcut,alpha, accval_g, Lvdtmat,...
lvdtcons, accbiasV, accsensi, filtertype...
,filtermethod,firorder);
[LVDTfilt, filtered_disp, filtered_vel, filtered_acc] ...
= accelo2disp(time,Ts, Fs, Fcut,alpha, accval, Lvdtmat,...
lvdtcons, accbiasV, accsensi, filtertype...
,filtermethod,firorder);
%% Compute the frequency
%--------------------------------------------------------------------------
% Compute the Fourier transform of the signal.
Y = fft(filtered_acc);
% Compute the two-sided spectrum P2. Then compute the single-sided spectrum P1
% based on P2 and the even-valued signal length L.
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
% Define the frequency domain f and plot the single-sided amplitude spectrum P1.
% On average, longer signals produce better frequency approximations.
f = Fs*(0:(L/2))/L;
%% Plot Acceleration vs.time
%--------------------------------------------------------------------------
figure;
subplot(5,2,1)
ax1 = plot(time, accval_g, 'LineWidth', 1);
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Acceleration ($g$)','Interpreter', 'latex');
title('Acceleration vs.time (with DC bias)')
ax2 = subplot(5,2,2);
plot(time, filtered_acc_g, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Acceleration ($g$)','Interpreter', 'latex');
title('Acceleration vs.time (DC bias removed)')
ax3 = subplot(5,2,3:4);
plot(time,filtered_acc, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Acceleration ($\frac{m}{s^2}$)','Interpreter', 'latex');
title('Acceleration vs.time (DC bias removed)')
ax4 = subplot(5,2,5:6);
plot(time,filtered_vel, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Velocity ($\frac{m}{s}$)','Interpreter', 'latex');
title('Velocity vs.time')
ax5 = subplot(5,2,7:8);
plot(time,filtered_disp, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Displacement ($m$)','Interpreter', 'latex');
title('Displacement vs.time')
ax6 = subplot(5,2,9:10);
plot(f,P1, 'LineWidth', 1)
grid on
title('Frequency Spectrum of Acceleration')
xlabel('f(Hz)')
ylabel('|P1(f)|')
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
1. 王思远, 张逸凡. (2016). 基于MEMS加速度计测量的速度和位移测量方法. 精仪与检测技术, 4, 29-32.
2. 刘兆岑, 张进杰, 吴树荣等. (2018). 加速度传感器信号滤波技术及其在位移测量中的应用. 自动化仪表, 39(5), 38-42.
3. 马靖蒙, 黄艺帆, 赵晨曦等. (2017). 基于自适应滤波和积分的加速度测速算法. 机械工程学报, 53(3), 68-74.
4. 高素平, 汪思悦, 毛亚伟等. (2016). 基于加速度测量的振动位移自适应无源解调算法. 哈尔滨工程大学学报, 37(5), 683-688.
🌈4 Matlab代码实现
相关文章:

【使用 DSP 滤波器加速速度和位移】使用信号处理算法过滤加速度数据并将其转换为速度和位移研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
家居行业解决方案 | 君子签电子签约助力家居企业减负增效
过去,家居行业因供需两端碎片化、服务链条较长等因素,导致线上发展较为缓慢,近年来,互联网的发展推动直播电商、兴趣电商兴起,促使家居行业数字化建设需求越来越为迫切。 合同管理作为家居行业企业经营的一项重要管理…...
Nodejs 第五章(Npm run 原理)
npm run xxx 发生了什么 按照下面的例子npm run dev 举例过程中发生了什么 读取package json 的scripts 对应的脚本命令(dev:vite),vite是个可执行脚本,他的查找规则是: 先从当前项目的node_modules/.bin去查找可执行命令vite如果没找到就去全局的node…...

150. 逆波兰表达式求值
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。 请你计算该表达式。返回一个表示表达式值的整数。 注意: 有效的算符为 、-、* 和 / 。 每个操作数(运算对象)都可以是一个整数或者另一个表达式。 两个…...
js中的设计模式
设计模式 代码整体的结构会更加清楚,管理起来会更加方便,更好地维护 设计模式是一种思想 发布订阅 模块化开发 导入很多模块 容器即数组存储未来要执行的方法,同addEventListener 数组塌陷问题* 由于删除了元素,导致从删除元素的位…...

PostgreSQL:string_agg 多列值聚合成一列
PostgreSQL:string_agg 多列值聚合成一列 string_agg是PostgreSQL中的一个聚合函数,用于将一组值连接为一个字符串。它接受两个参数:要连接的值和连接符。 语法如下: string_agg(expression, delimiter)其中,expression是要连接…...
通向架构师的道路之apache_tomcat_https应用
一、总结前一天的学习 通过上一章我们知道、了解并掌握了Web Server结合App Server是怎么样的一种架构,并且亲手通过Apache的Http Server与Tomcat6进行了整合的实验。 这样的架构的好处在于: 减轻App Server端的压力,用Web Server来分压…...

iOS——锁与死锁问题
iOS中的锁 什么是锁锁的分类互斥锁1. synchronized2. NSLock3. pthread 递归锁1. NSRecursiveLock2. pthread 信号量Semaphore1. dispatch_semaphore_t2. pthread 条件锁1. NSCodition2. NSCoditionLock3. POSIX Conditions 分布式锁NSDistributedLock 读写锁1. dispatch_barri…...

恒运资本:股票总市值是什么意思?
职业新手可能会疑惑地问,股票总市值到底是什么意思?究竟,这是普通出资者常常看到的词汇,要了解股票总市值的含义,是需求了解金融商场的基本概念的。 股票总市值简介 股票的总市值是由公司一切的股票的数量乘以现在的价…...
Selenium Chrome Webdriver 如何获取 Youtube 悬停文本
导语 Youtube 是一个非常流行的视频分享平台,有时候我们可能想要爬取一些视频的信息,比如标题、播放量、点赞数等。但是有些信息并不是直接显示在网页上的,而是需要我们将鼠标悬停在某个元素上才能看到,比如视频的时长、上传时间…...
【LeetCode每日一题】——766.托普利茨矩阵
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【题目进阶】八【解题思路】九【时间频度】十【代码实现】十一【提交结果】 一【题目类别】 矩阵 二【题目难度】 简单 三【题目编号】 766.托普利茨矩阵 四【题目描述…...
第三方材料检测实验室LIMS系统源码 lims源码
实验室LIMS系统采用国际规范的业务管理流程和严格的质量控制体系,对每个检测流程节点采用 “人、机、料、法、环、测”进行质量控制,可记录,可追溯。强大的数据查询和统计分析能力,提高工作效率;自动化地采集实验室原始…...

【数据结构与算法——TypeScript】数组、栈、队列、链表
【数据结构与算法——TypeScript】 算法(Algorithm)的认识 解决问题的过程中,不仅仅 数据的存储方式会影响效率,算法的优劣也会影响效率 什么是算法? 定义: 🟢 一个有限指令集,每条指令的描述不依赖于言语…...

[运维|中间件] Apache APISIX使用笔记
简介 Apache APISIX 是一个现代化、高性能、可扩展的开源 API 网关和微服务管理平台。 安装 快速安装 curl -sL https://run.api7.ai/apisix/quickstart | sh...
)
Android Intent 使用(详细版)
经典好文推荐,通过阅读本文,您将收获以下知识点: 一、通过组件名启动 二、通过包名、类名启动 三、通过类启动 四、打电话 五、发短信 六、打开网页 七、播放音乐 八、打开图片 九、创建闹钟 十、创建定时器 十一、添加日历事件 十二、拍照 十三、打开Camera 十四、打开视频录…...

【Clion 2】多行TODO使用
一、TODO: 说明: 有时需要标记部分代码以供将来参考: 优化和改进的领域、可能的更改、要讨论的问题等等。 支持: TODO和FIXME小写和大写。这些模式可以在任何受支持的文件类型的行注释和块注释内使用。 创建TODO项 在要添加注释的代码行中…...

【运维】hive 终端突然不能使用:Hive Schema version does not match metastore‘s schema version
文章目录 一. 问题描述二. 常规排查1. 元数据库2. hive-site.xml相关meta连接信息检查 三. 正解 一. 问题描述 进入hive终端,执行如下命令报错: hive> show tables; FAILED: SemanticException org.apache.hadoop.hive.ql.metadata.HiveException: …...

P1049 [NOIP2001 普及组] 装箱问题
题目描述 有一个箱子容量为 V,同时有 n 个物品,每个物品有一个体积。 现在从 n 个物品中,任取若干个装入箱内(也可以不取),使箱子的剩余空间最小。输出这个最小值。 输入格式 第一行共一个整数 V&#…...

QCustomPlot获取选点坐标
QCustomPlot版本:Version: 2.1.1 设置点选择模式 customPlot->setInteractions(QCP::iSelectPlottables);2.绑定点击事件 connect(customPlot, &QCustomPlot::plottableClick, this, &CCustomPlot::onPlotClick);3.读取点位置 void CustomPlot::onP…...

Qt配置Android开发
1.使用Qt5.14.2 2.安装java和SDK,NDK 具体参考该博客【原创】基于Qt5.14的一站式安卓开发环境搭建_qt安卓开发环境搭建_Jamie.T的博客-CSDN博客 3.后续可能会遇到的问题: ①SDK配置问题: 若出现以下编译错误,是build-tools 2…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

