【LeetCode每日一题】——766.托普利茨矩阵
文章目录
- 一【题目类别】
- 二【题目难度】
- 三【题目编号】
- 四【题目描述】
- 五【题目示例】
- 六【题目提示】
- 七【题目进阶】
- 八【解题思路】
- 九【时间频度】
- 十【代码实现】
- 十一【提交结果】
一【题目类别】
- 矩阵
二【题目难度】
- 简单
三【题目编号】
- 766.托普利茨矩阵
四【题目描述】
- 给你一个 m x n 的矩阵 matrix 。如果这个矩阵是托普利茨矩阵,返回 true ;否则,返回 false 。
- 如果矩阵上每一条由左上到右下的对角线上的元素都相同,那么这个矩阵是 托普利茨矩阵 。
五【题目示例】
-
示例 1:
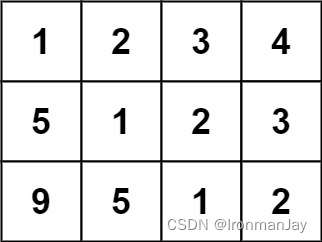
- 输入:matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
- 输出:true
- 解释:
- 在上述矩阵中, 其对角线为:
- “[9]”, “[5, 5]”, “[1, 1, 1]”, “[2, 2, 2]”, “[3, 3]”, “[4]”。
- 各条对角线上的所有元素均相同, 因此答案是 True 。
-
示例 2:

- 输入:matrix = [[1,2],[2,2]]
- 输出:false
- 解释:
- 对角线 “[1, 2]” 上的元素不同。
六【题目提示】
- m = = m a t r i x . l e n g t h m == matrix.length m==matrix.length
- n = = m a t r i x [ i ] . l e n g t h n == matrix[i].length n==matrix[i].length
- 1 < = m , n < = 20 1 <= m, n <= 20 1<=m,n<=20
- 0 < = m a t r i x [ i ] [ j ] < = 99 0 <= matrix[i][j] <= 99 0<=matrix[i][j]<=99
七【题目进阶】
- 如果矩阵存储在磁盘上,并且内存有限,以至于一次最多只能将矩阵的一行加载到内存中,该怎么办?
- 如果矩阵太大,以至于一次只能将不完整的一行加载到内存中,该怎么办?
八【解题思路】
- 本题的思路比较简单,我们无需逐个对角线去比较,只需要比较前一行除了最后一个元素和后一行除了第一个元素后剩余的元素是否想等
- 因为如果是托普利茨矩阵的话,下一行一定是上一行向右移动一个位置之后形成的矩阵,所以上一行的最后一个元素和下一行的第一个元素,可以无须判断,因为上一行的最后一个元素被移出了,下一行的第一个元素单独成为对角线
- 最后返回结果即可
九【时间频度】
- 时间复杂度: O ( m ∗ n ) O(m * n) O(m∗n), m 、 n m、n m、n分别为传入数组的行数和列数
- 空间复杂度: O ( 1 ) O(1) O(1)
十【代码实现】
- Java语言版
class Solution {public boolean isToeplitzMatrix(int[][] matrix) {int m = matrix.length;int n = matrix[0].length;for(int i = 0;i < m - 1;i++){for(int j = 0;j < n - 1;j++){if(matrix[i][j] != matrix[i+1][j+1]){return false;}}}return true;}
}
- C语言版
bool isToeplitzMatrix(int** matrix, int matrixSize, int* matrixColSize)
{int m = matrixSize;int n = matrixColSize[0];for(int i = 0;i < m - 1;i++){for(int j = 0;j < n - 1;j++){if(matrix[i][j] != matrix[i+1][j+1]){return false;}}}return true;
}
- Python语言版
class Solution:def isToeplitzMatrix(self, matrix: List[List[int]]) -> bool:m = len(matrix)n = len(matrix[0])for i in range(m - 1):for j in range(n - 1):if matrix[i][j] != matrix[i+1][j+1]:return Falsereturn True
- C++语言版
class Solution {
public:bool isToeplitzMatrix(vector<vector<int>>& matrix) {int m = matrix.size();int n = matrix[0].size();for(int i = 0;i < m - 1;i++){for(int j = 0;j < n - 1;j++){if(matrix[i][j] != matrix[i+1][j+1]){return false;}}}return true;}
};
十一【提交结果】
-
Java语言版
-
C语言版

-
Python语言版

-
C++语言版
相关文章:

【LeetCode每日一题】——766.托普利茨矩阵
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【题目进阶】八【解题思路】九【时间频度】十【代码实现】十一【提交结果】 一【题目类别】 矩阵 二【题目难度】 简单 三【题目编号】 766.托普利茨矩阵 四【题目描述…...
第三方材料检测实验室LIMS系统源码 lims源码
实验室LIMS系统采用国际规范的业务管理流程和严格的质量控制体系,对每个检测流程节点采用 “人、机、料、法、环、测”进行质量控制,可记录,可追溯。强大的数据查询和统计分析能力,提高工作效率;自动化地采集实验室原始…...

【数据结构与算法——TypeScript】数组、栈、队列、链表
【数据结构与算法——TypeScript】 算法(Algorithm)的认识 解决问题的过程中,不仅仅 数据的存储方式会影响效率,算法的优劣也会影响效率 什么是算法? 定义: 🟢 一个有限指令集,每条指令的描述不依赖于言语…...

[运维|中间件] Apache APISIX使用笔记
简介 Apache APISIX 是一个现代化、高性能、可扩展的开源 API 网关和微服务管理平台。 安装 快速安装 curl -sL https://run.api7.ai/apisix/quickstart | sh...
)
Android Intent 使用(详细版)
经典好文推荐,通过阅读本文,您将收获以下知识点: 一、通过组件名启动 二、通过包名、类名启动 三、通过类启动 四、打电话 五、发短信 六、打开网页 七、播放音乐 八、打开图片 九、创建闹钟 十、创建定时器 十一、添加日历事件 十二、拍照 十三、打开Camera 十四、打开视频录…...

【Clion 2】多行TODO使用
一、TODO: 说明: 有时需要标记部分代码以供将来参考: 优化和改进的领域、可能的更改、要讨论的问题等等。 支持: TODO和FIXME小写和大写。这些模式可以在任何受支持的文件类型的行注释和块注释内使用。 创建TODO项 在要添加注释的代码行中…...

【运维】hive 终端突然不能使用:Hive Schema version does not match metastore‘s schema version
文章目录 一. 问题描述二. 常规排查1. 元数据库2. hive-site.xml相关meta连接信息检查 三. 正解 一. 问题描述 进入hive终端,执行如下命令报错: hive> show tables; FAILED: SemanticException org.apache.hadoop.hive.ql.metadata.HiveException: …...

P1049 [NOIP2001 普及组] 装箱问题
题目描述 有一个箱子容量为 V,同时有 n 个物品,每个物品有一个体积。 现在从 n 个物品中,任取若干个装入箱内(也可以不取),使箱子的剩余空间最小。输出这个最小值。 输入格式 第一行共一个整数 V&#…...

QCustomPlot获取选点坐标
QCustomPlot版本:Version: 2.1.1 设置点选择模式 customPlot->setInteractions(QCP::iSelectPlottables);2.绑定点击事件 connect(customPlot, &QCustomPlot::plottableClick, this, &CCustomPlot::onPlotClick);3.读取点位置 void CustomPlot::onP…...

Qt配置Android开发
1.使用Qt5.14.2 2.安装java和SDK,NDK 具体参考该博客【原创】基于Qt5.14的一站式安卓开发环境搭建_qt安卓开发环境搭建_Jamie.T的博客-CSDN博客 3.后续可能会遇到的问题: ①SDK配置问题: 若出现以下编译错误,是build-tools 2…...
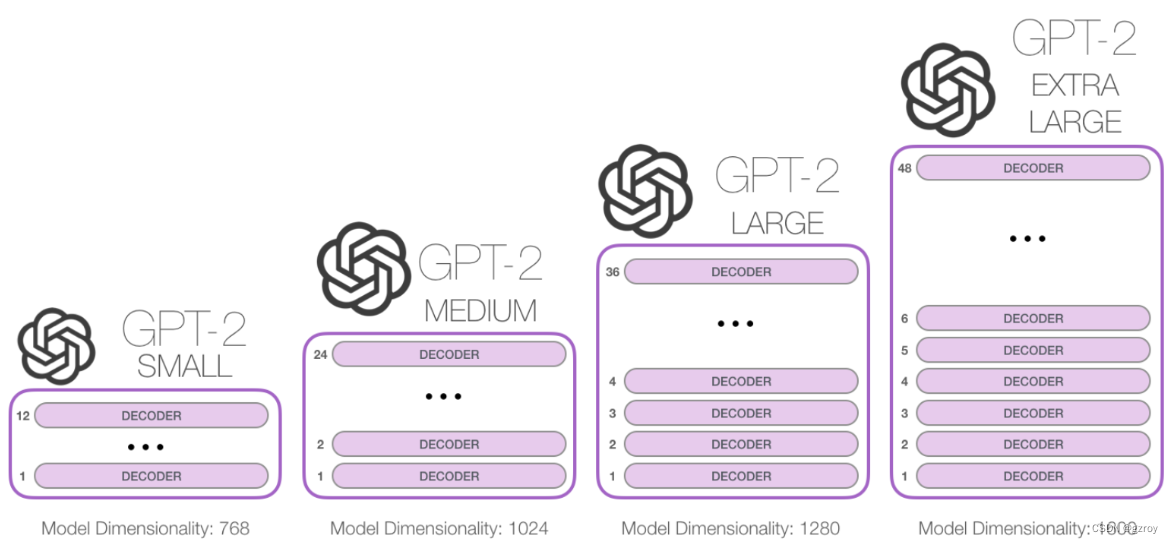
花费7元训练自己的GPT 2模型
在上一篇博客中,我介绍了用Tensorflow来重现GPT 1的模型和训练的过程。这次我打算用Pytorch来重现GPT 2的模型并从头进行训练。 GPT 2的模型相比GPT 1的改进并不多,主要在以下方面: 1. GPT 2把layer normalization放在每个decoder block的前…...

性能分析工具
性能分析工具 valgrind 交叉编译 android arm/arm64 平台 valgrind android32 #!/usr/bin/env bashexport NDKROOT~/opt/android-ndk-r14b/ export AR$NDKROOT/toolchains/arm-linux-androideabi-4.9/prebuilt/linux-x86_64/bin/arm-linux-androideabi-ar export LD$NDKROO…...
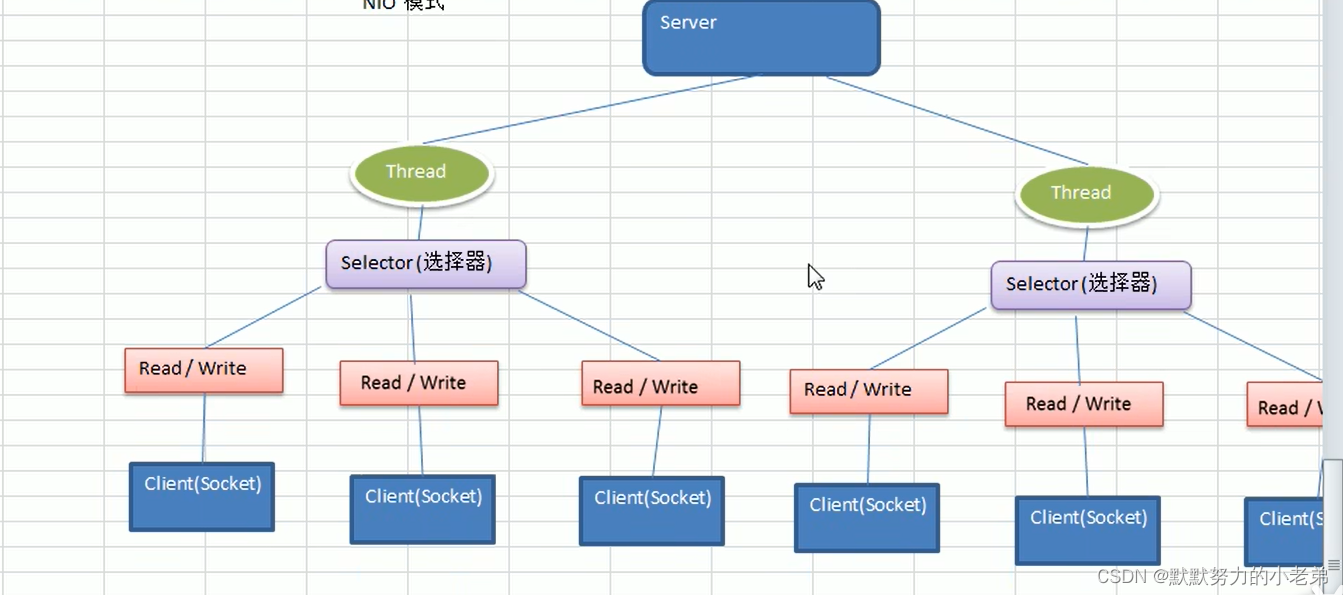
1.netty介绍
1.介绍 是JBOSS通过的java开源框架是异步的,基于事件驱动(点击一个按钮调用某个函数)的网络应用框架,高性能高可靠的网络IO程序基于TCP,面向客户端高并发应用/点对点大量数据持续传输的应用是NIO框架 (IO的一层层封装) TCP/IP->javaIO和网络编程–>NIO—>Netty 2.应用…...

【Jmeter】压测mysql数据库中间件mycat
目录 背景 环境准备 1、下载Jmeter 2、下载mysql数据库的驱动包 3、要进行测试的数据库 Jmeter配置 1、启动Jmeter图形界面 2、加载mysql驱动包 3、新建一个线程组,然后如下图所示添加 JDBC Connection Configuration 4、配置JDBC Connection Configurati…...
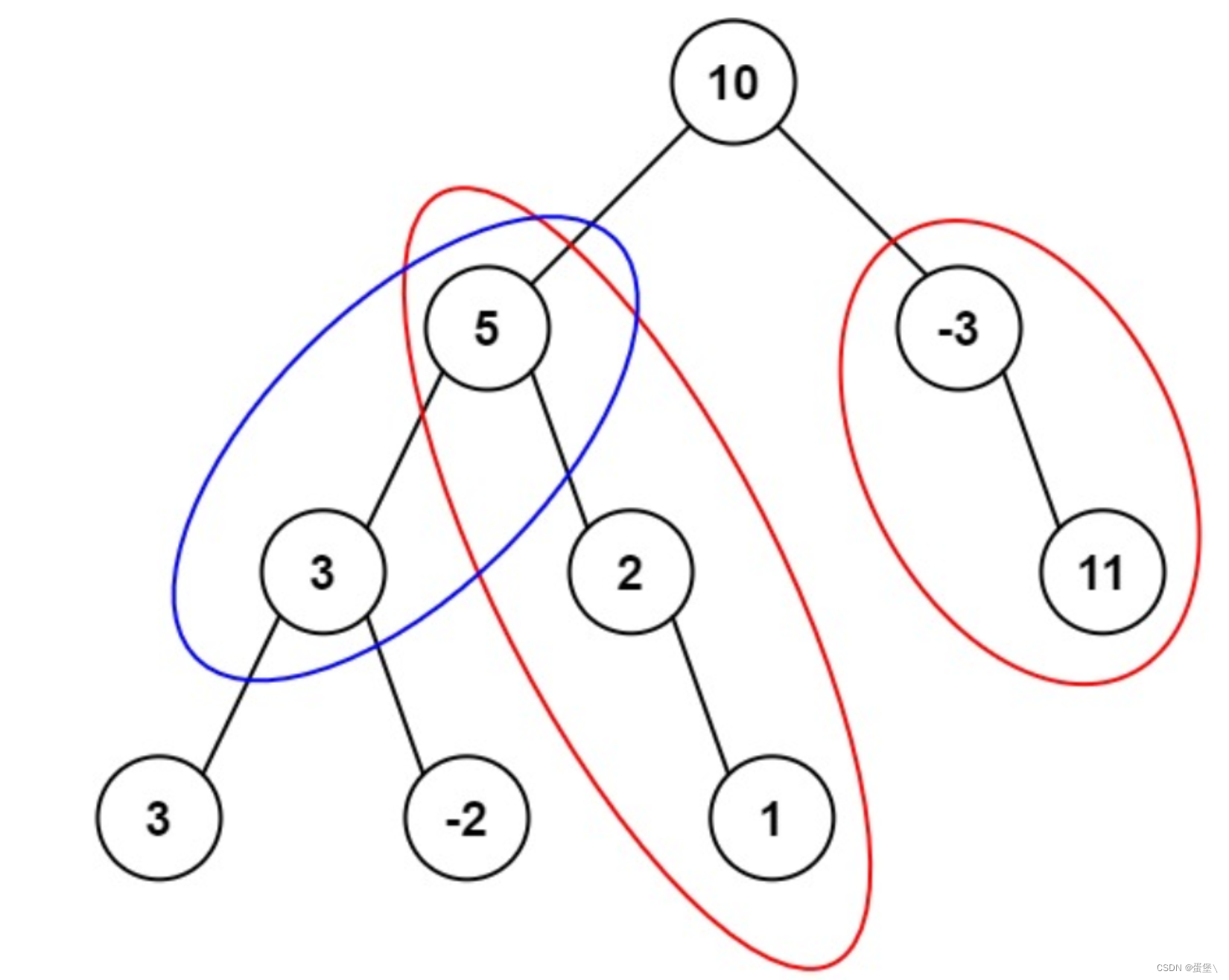
leetcode原题 路径总和 I II III(递归实现)
路径总和 I : 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。…...

【css】css设置表格样式-边框线合并
<style> table, td, th {border: 1px solid black;//设置边框线 }table {width: 100%; }td {text-align: center;//设置文本居中 } </style> </head> <body><table><tr><th>Firstname</th><th>Lastname</th><t…...
使用Flutter的image_picker插件实现设备的相册的访问和拍照
文章目录 需求描述Flutter插件image_picker的介绍使用步骤1、添加依赖2、导入 例子完整的代码效果 总结 需求描述 在应用开发时,我们有很多场景要使用到更换图片的功能,即将原本的图像替换设置成其他的图像,从设备的相册或相机中选择图片或拍…...

数学建模体系
1评价类 主观求权重:层次分析法客观求权重:TOPSIS综合评价:典型相关分析 2预测插值算法拟合多元回归分析时间序列分析、ARCH和garch模型岭回归和lasso回归 3关系相关系数典型相关分析多元回归分析灰色关联分析 4图最短路径:迪杰斯…...
13.7 CentOS 7 环境下大量创建帐号的方法
13.7.1 一些帐号相关的检查工具 pwck pwck 这个指令在检查 /etc/passwd 这个帐号配置文件内的信息,与实际的主文件夹是否存在等信息, 还可以比对 /etc/passwd /etc/shadow 的信息是否一致,另外,如果 /etc/passwd 内的数据字段错…...
HTML5 Canvas(画布)
<canvas>标签定义图形,比如图表和其他图像,你必须用脚本来绘制图形。 在画布上( Canvas )画一个共红色矩形,渐变矩形,彩色矩形,和一些彩色文字。 什么是 Canvas? HTML5<c…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
