leetcode原题 路径总和 I II III(递归实现)
路径总和 I :
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
要点:判断是否存在满足条件的路径,只需返回true or false。

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
解题思路:
每遍历一个节点,就从targetsum中减去当前节点的值,当遍历到叶子节点时,如果targetsum=0,说明存在该路径,返回true。反之,返回false
class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if(root==nullptr) return false;targetSum-=root->val;if(root->left==nullptr&&root->right==nullptr){return targetSum==0;}//左子树和右子树有一个满足就可以,所以用||的关系return hasPathSum(root->left,targetSum)||hasPathSum(root->right,targetSum);}
};
路径总和 II:
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
要点:返回所有满足题意的路径,必须是从根节点开始,叶子节点结束。

输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
解题思路:
添加一个临时数组,用来存放当前遍历到的节点走过的路径。其他的与第一题相同,找到符合题意的路径,就将临时数组存放到结果数组中,若不符合条件,需回退,注意回退时需要将将一个放到临时数组中的节点删掉。
class Solution {
public:vector<vector<int>> res;//所有路径vector<int> temp;//当前路径void dfs(TreeNode* root, int targetSum){if(root==nullptr) return;temp.push_back(root->val);//当前节点放入到temp中targetSum-=root->val;//从总和中减去//若遇到叶子节点,需判断目标值是否已经为0if(root->left==nullptr&&root->right==nullptr){//目标值=0,说明当前路径符合题意,temp放到res中if(targetSum==0){res.push_back(temp);}}//递归dfs(root->left,targetSum);dfs(root->right,targetSum);//不符合题意,将当前节点从路径中删掉temp.pop_back();}vector<vector<int>> pathSum(TreeNode* root, int targetSum) {dfs(root,targetSum);return res;}
};路径总和 III:
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
要点:返回的是所有符合题意的路径总条数,与第二题不一样的是,可以不是从根节点开始,也不需要在叶子节点结束。
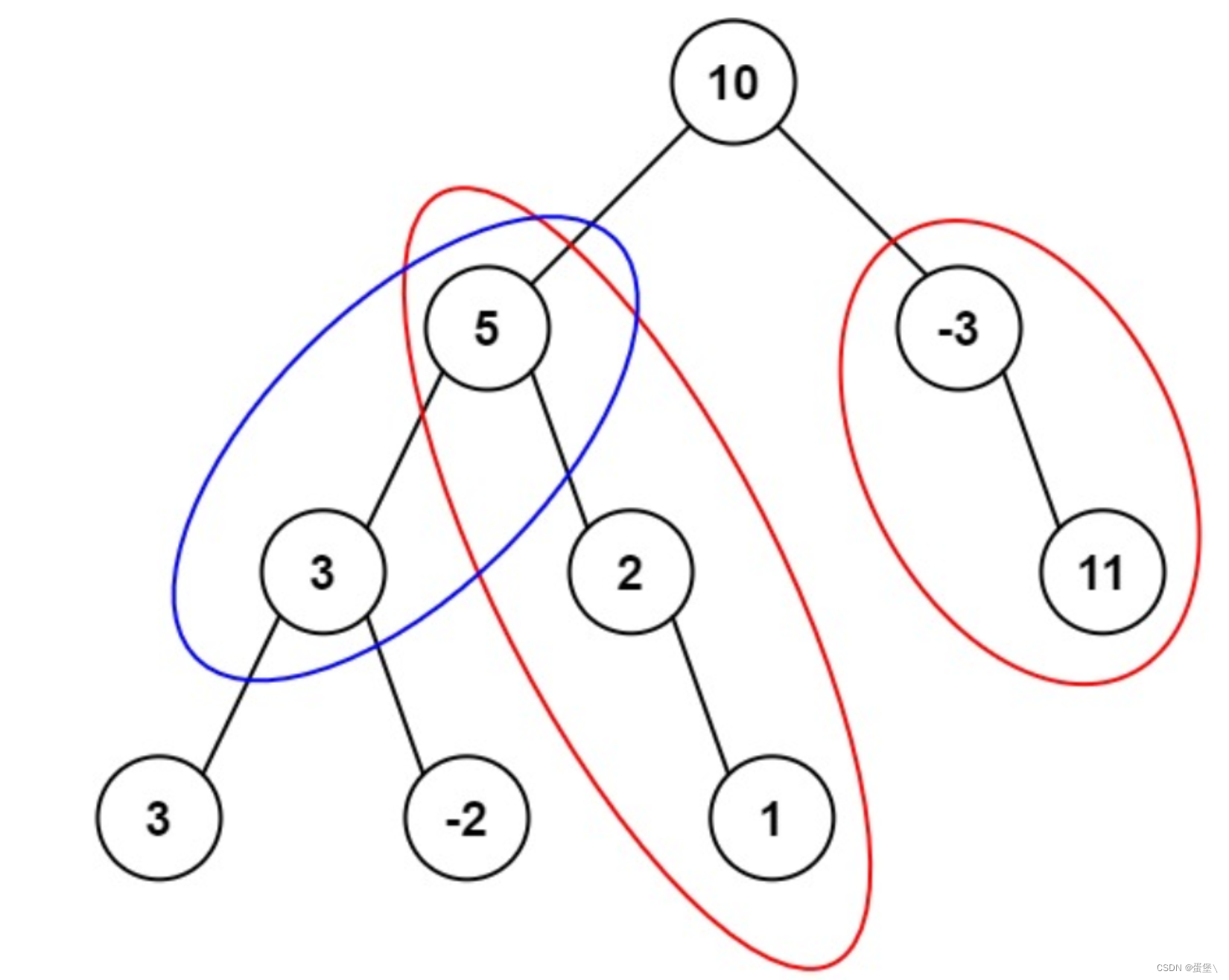
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示。
解题思路:
相当于是递归套递归,构建一个找路径函数,遍历以当前节点为起始的路径中,是否存在符合题意的路径,然后再在原函数递归到每一个节点,使每一个节点都为起始节点进行找符合题意的路径。
class Solution {
public:int res=0;int pathSum(TreeNode* root, int targetSum) {if(root==nullptr) return res;find_path(root,targetSum);//以当前的root节点为起始节点,找路径pathSum(root->left,targetSum);//递归当前根节点的左子树上的节点pathSum(root->right,targetSum);//递归当前根节点的右子树上的节点return res;}//找路径函数void find_path(TreeNode* root,long targetSum){if(root==nullptr) return;targetSum -= root->val;if(targetSum==0)//只要targetsum=0,说明存在一条路径,那么res++{res+=1;}find_path(root->left,targetSum);find_path(root->right,targetSum);}
};相关文章:

leetcode原题 路径总和 I II III(递归实现)
路径总和 I : 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。…...

【css】css设置表格样式-边框线合并
<style> table, td, th {border: 1px solid black;//设置边框线 }table {width: 100%; }td {text-align: center;//设置文本居中 } </style> </head> <body><table><tr><th>Firstname</th><th>Lastname</th><t…...
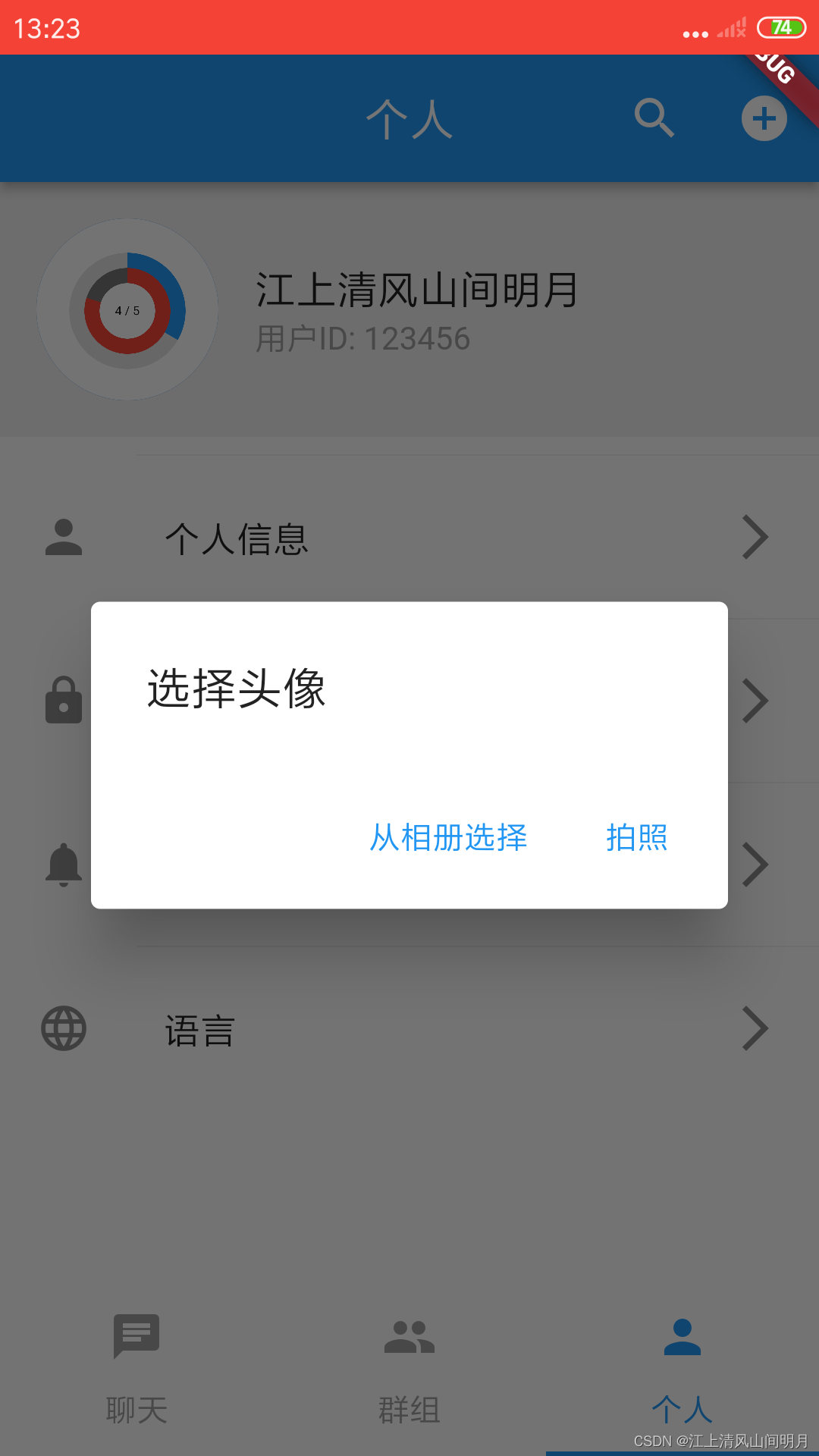
使用Flutter的image_picker插件实现设备的相册的访问和拍照
文章目录 需求描述Flutter插件image_picker的介绍使用步骤1、添加依赖2、导入 例子完整的代码效果 总结 需求描述 在应用开发时,我们有很多场景要使用到更换图片的功能,即将原本的图像替换设置成其他的图像,从设备的相册或相机中选择图片或拍…...

数学建模体系
1评价类 主观求权重:层次分析法客观求权重:TOPSIS综合评价:典型相关分析 2预测插值算法拟合多元回归分析时间序列分析、ARCH和garch模型岭回归和lasso回归 3关系相关系数典型相关分析多元回归分析灰色关联分析 4图最短路径:迪杰斯…...
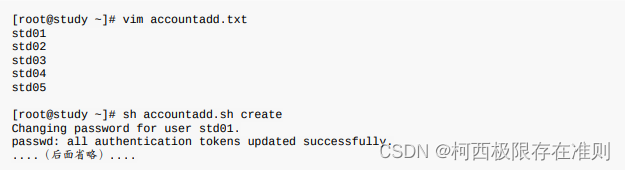
13.7 CentOS 7 环境下大量创建帐号的方法
13.7.1 一些帐号相关的检查工具 pwck pwck 这个指令在检查 /etc/passwd 这个帐号配置文件内的信息,与实际的主文件夹是否存在等信息, 还可以比对 /etc/passwd /etc/shadow 的信息是否一致,另外,如果 /etc/passwd 内的数据字段错…...
HTML5 Canvas(画布)
<canvas>标签定义图形,比如图表和其他图像,你必须用脚本来绘制图形。 在画布上( Canvas )画一个共红色矩形,渐变矩形,彩色矩形,和一些彩色文字。 什么是 Canvas? HTML5<c…...

io的异常处理以及properties
try(流对象的创建) { 对象的处理逻辑} catch(IOException e) { 异常的处理逻辑} public static void test4(){try(FileWriter fwnew FileWriter("a.txt",true); ){char[] cbuf{a};//写入一个字符串组fw.write(cbuf);}catch(IOException e){e.printStackTrace();}}上面…...
Linux下基于Dockerfile构建镜像应用(1)
目录 基于已有容器创建镜像 Dockerfile构建SSHD镜像 构建镜像 测试容器 可以登陆 Dockerfile构建httpd镜像 构建镜像 测试容器 Dockerfile构建nginx镜像 构建镜像 概述: Docker 镜像是Docker容器技术中的核心,也是应用打包构建发布的标准格式。…...

JS中常见的模块管理规范梳理
一、CommonJS规范 CommonJS规范是一种用于JavaScript模块化开发的规范,它定义了模块的导入、导出方式和加载机制,主要用在Node开发中。 1. 使用场景 服务器端开发:Node.js是使用CommonJS规范的,因此在服务器端开发中࿰…...

3维空间下按平面和圆柱面上排版设计
AR空间中将若干平面窗口排列在指定平面或圆柱体面上 平面排版思路 指定平面方向向量layout_centre ,平面上的一点作为排版版面的中心layout_position float3 layout_position = float3(0,0,-10); float3 layout_centre = float3(0,0,1...
【Spring框架】Spring AOP
目录 什么是AOP?AOP组成Spring AOP 实现步骤Spring AOP实现原理JDK Proxy VS CGLIB 什么是AOP? AOP(Aspect Oriented Programming):⾯向切⾯编程,它是⼀种思想,它是对某⼀类事情的集中处理。⽐如…...

寻找旋转排序数组中的最小值——力扣153
文章目录 题目描述解法 二分法 题目描述 解法 二分法 int findMin(vector<int>& nums){int l0, rnums.size()-1;while(l<r){int mid (lr)/2;if(nums[mid]<nums[r]) rmid;else lmid1;}return nums[l];}...
安卓逆向 - 基础入门教程
一、引言 1、我们在采集app数据时,有些字段是加密的,如某麦网x-mini-wua x-sgext x-sign x-umt x-utdid等参数,这时候我们需要去分析加密字段的生成。本篇将以采集的角度讲解入门安卓逆向需要掌握的技能、工具。 2、安卓(Androi…...
验证码安全志:AIGC+集成环境信息信息检测
目录 知己知彼,黑灰产破解验证码的过程 AIGC加持,防范黑灰产的破解 魔高一丈,黑灰产AIGC突破常规验证码 双重防护,保障验证码安全 黑灰产经常采用批量撞库方式登录用户账号,然后进行违法违规操作。 黑灰产将各种方…...
R-Meta分析教程
详情点击链接:R-Meta模型教程 一:Meta分析的选题与文献计量分析CiteSpace应用 1、Meta分析的选题与文献检索 1)什么是Meta分析? 2)Meta分析的选题策略 3)文献检索数据库 4)精确检索策略,如何检索全、检索准 5)文献的管理与…...
【3维视觉】3D空间常用算法(点到直线距离、面法线、二面角)
3D空间点到直线的距离 3D空间点到直线的距离 3D空间的曲率 三维空间有三个基本元素,点,线,面。那么曲率是如何定义的呢? 点的曲率? 线的曲率? 面的曲率? 法曲率 设曲面上的曲线在某一点处的切…...
Nodejs 第四章(Npm install 原理)
在执行npm install 的时候发生了什么? 首先安装的依赖都会存放在根目录的node_modules,默认采用扁平化的方式安装,并且排序规则.bin第一个然后系列,再然后按照首字母排序abcd等,并且使用的算法是广度优先遍历,在遍历依…...
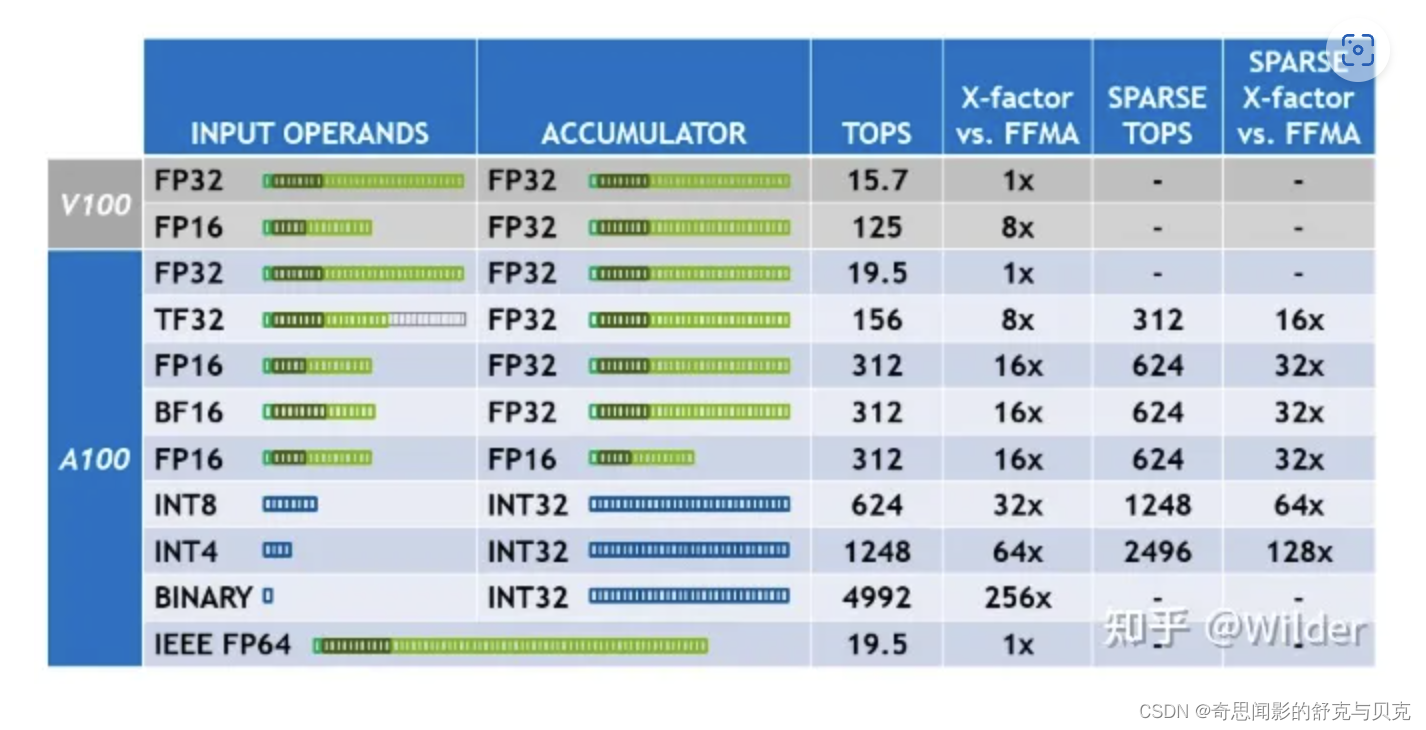
[深度学习] GPU处理能力(TFLOPS/TOPS)
计算能力换算 理论峰值 = GPU芯片数量GPU Boost主频核心数量*单个时钟周期内能处理的浮点计算次数 只不过在GPU里单精度和双精度的浮点计算能力需要分开计算,以最新的Tesla P100为例: 双精度理论峰值 = FP64 Cores *…...

js:获取浏览器默认语言
实现代码 navigator.language zh-CN参考文章 [javascript] js如何获取浏览器的语言...
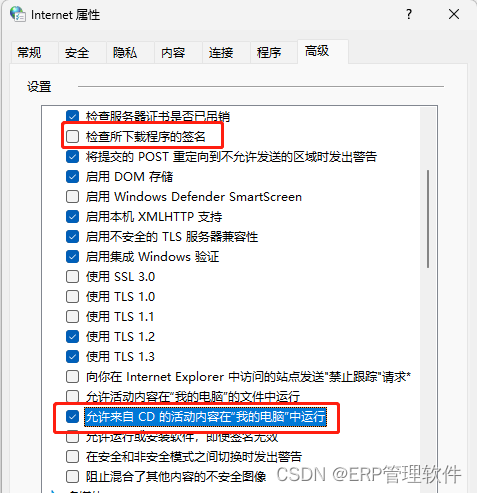
【U8+】用友U8重新注册加密锁,提示:写卡失败,请重新配置客户端控件。
【问题描述】 用友U8软件重新安装后,需要重新注册加密锁激活软件。 注册反馈提示:产品注册失败。 原因(1):写卡失败,请重新配置客户端控件。 【解决方法】 1、打开控制面板,网络和 Internet&a…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
