io的异常处理以及properties
- try(流对象的创建) { 对象的处理逻辑} catch(IOException e) { 异常的处理逻辑}
public static void test4(){try(FileWriter fw=new FileWriter("a.txt",true); ){char[] cbuf={'a'};//写入一个字符串组fw.write(cbuf);}catch(IOException e){e.printStackTrace();}}
- 上面的流对象可以多个,并且最后不必调用close,会在执行完毕之后自动close
Properties是一个双列集合,key和value默认都是字符串
常见方法:
Object setProperty(String key ,String value) 调用Hashtable的方法put
String getProperty(String key)通过key来获取对应的value
Set stringPropertyNames()返回列表的键的集合
public static void test5() {Properties pro=new Properties();pro.setProperty("zs","19");pro.setProperty("ls","18");pro.setProperty("ww","17");Set<String> keys=pro.stringPropertyNames();for (String key : keys) {System.out.println(pro.getProperty(key));}}
- 保存流对象的使用步骤
创建properties集合对象,添加数据
创建字符或者字节输出流对象,绑定输出文件
使用properties对象的store方法,把集合中的临时数据持久化的保存到硬盘中保存
public static void test6() throws IOException {Properties pro=new Properties();pro.setProperty("zs","19");pro.setProperty("ls","18");pro.setProperty("ww","17");FileWriter fw=new FileWriter("pro.txt");pro.store(fw,"集合");fw.close();}
- 从文件中拂去流对象的步骤
创建properties对象
创建字符或者字节输出流对象FileReader,绑定输出文件
使用properties对象的load方法传入FileReader对象
利用properties对象的stringPropertyNames方法获取所有键
利用properties对象的getProperty获取值
public static void test7() throws IOException {FileReader fr=new FileReader("pro.txt");Properties pr=new Properties();pr.load(fr);Set<String> keys=pr.stringPropertyNames();for (String key : keys) {System.out.println(pr.getProperty(key));}fr.close();}
相关文章:

io的异常处理以及properties
try(流对象的创建) { 对象的处理逻辑} catch(IOException e) { 异常的处理逻辑} public static void test4(){try(FileWriter fwnew FileWriter("a.txt",true); ){char[] cbuf{a};//写入一个字符串组fw.write(cbuf);}catch(IOException e){e.printStackTrace();}}上面…...
Linux下基于Dockerfile构建镜像应用(1)
目录 基于已有容器创建镜像 Dockerfile构建SSHD镜像 构建镜像 测试容器 可以登陆 Dockerfile构建httpd镜像 构建镜像 测试容器 Dockerfile构建nginx镜像 构建镜像 概述: Docker 镜像是Docker容器技术中的核心,也是应用打包构建发布的标准格式。…...

JS中常见的模块管理规范梳理
一、CommonJS规范 CommonJS规范是一种用于JavaScript模块化开发的规范,它定义了模块的导入、导出方式和加载机制,主要用在Node开发中。 1. 使用场景 服务器端开发:Node.js是使用CommonJS规范的,因此在服务器端开发中࿰…...

3维空间下按平面和圆柱面上排版设计
AR空间中将若干平面窗口排列在指定平面或圆柱体面上 平面排版思路 指定平面方向向量layout_centre ,平面上的一点作为排版版面的中心layout_position float3 layout_position = float3(0,0,-10); float3 layout_centre = float3(0,0,1...
【Spring框架】Spring AOP
目录 什么是AOP?AOP组成Spring AOP 实现步骤Spring AOP实现原理JDK Proxy VS CGLIB 什么是AOP? AOP(Aspect Oriented Programming):⾯向切⾯编程,它是⼀种思想,它是对某⼀类事情的集中处理。⽐如…...

寻找旋转排序数组中的最小值——力扣153
文章目录 题目描述解法 二分法 题目描述 解法 二分法 int findMin(vector<int>& nums){int l0, rnums.size()-1;while(l<r){int mid (lr)/2;if(nums[mid]<nums[r]) rmid;else lmid1;}return nums[l];}...
安卓逆向 - 基础入门教程
一、引言 1、我们在采集app数据时,有些字段是加密的,如某麦网x-mini-wua x-sgext x-sign x-umt x-utdid等参数,这时候我们需要去分析加密字段的生成。本篇将以采集的角度讲解入门安卓逆向需要掌握的技能、工具。 2、安卓(Androi…...
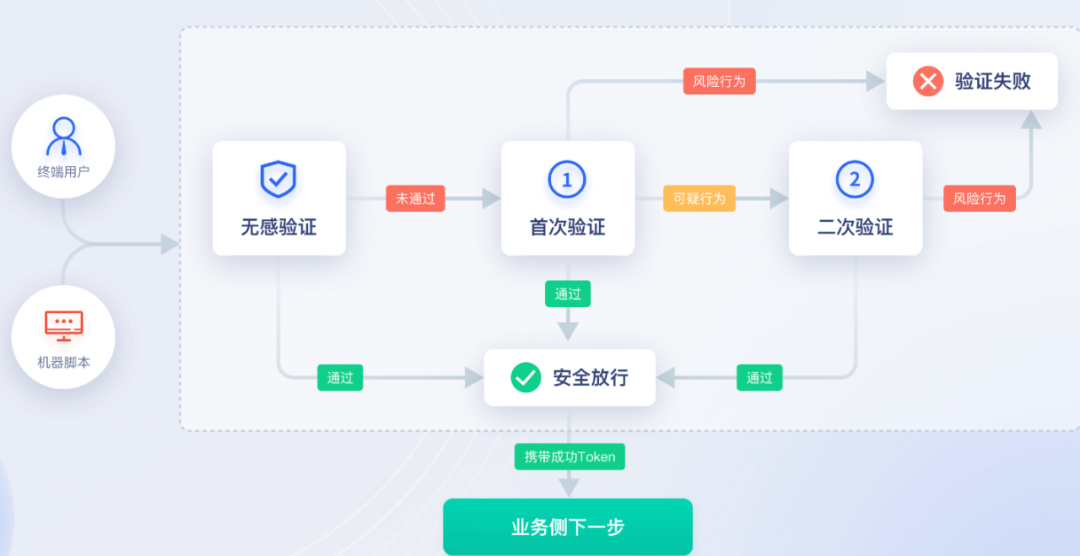
验证码安全志:AIGC+集成环境信息信息检测
目录 知己知彼,黑灰产破解验证码的过程 AIGC加持,防范黑灰产的破解 魔高一丈,黑灰产AIGC突破常规验证码 双重防护,保障验证码安全 黑灰产经常采用批量撞库方式登录用户账号,然后进行违法违规操作。 黑灰产将各种方…...
R-Meta分析教程
详情点击链接:R-Meta模型教程 一:Meta分析的选题与文献计量分析CiteSpace应用 1、Meta分析的选题与文献检索 1)什么是Meta分析? 2)Meta分析的选题策略 3)文献检索数据库 4)精确检索策略,如何检索全、检索准 5)文献的管理与…...
【3维视觉】3D空间常用算法(点到直线距离、面法线、二面角)
3D空间点到直线的距离 3D空间点到直线的距离 3D空间的曲率 三维空间有三个基本元素,点,线,面。那么曲率是如何定义的呢? 点的曲率? 线的曲率? 面的曲率? 法曲率 设曲面上的曲线在某一点处的切…...
Nodejs 第四章(Npm install 原理)
在执行npm install 的时候发生了什么? 首先安装的依赖都会存放在根目录的node_modules,默认采用扁平化的方式安装,并且排序规则.bin第一个然后系列,再然后按照首字母排序abcd等,并且使用的算法是广度优先遍历,在遍历依…...
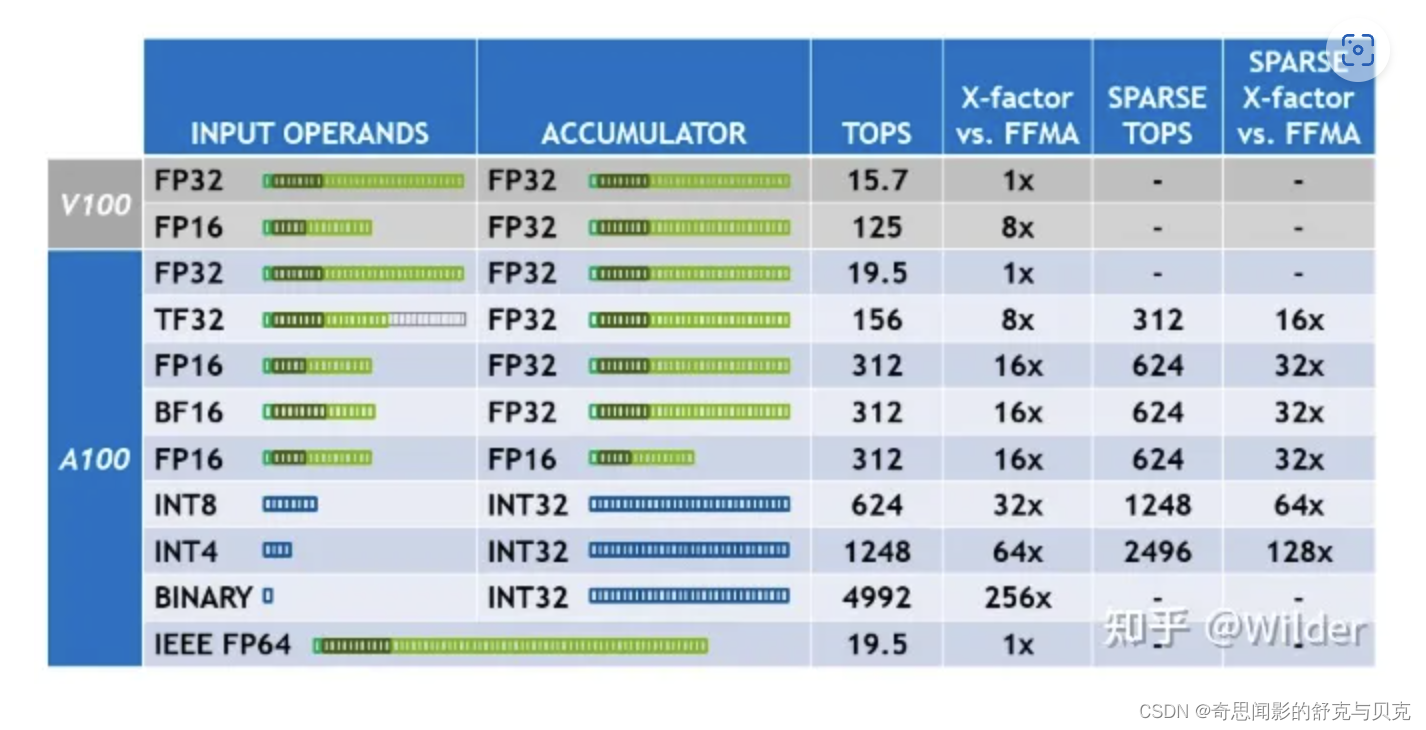
[深度学习] GPU处理能力(TFLOPS/TOPS)
计算能力换算 理论峰值 = GPU芯片数量GPU Boost主频核心数量*单个时钟周期内能处理的浮点计算次数 只不过在GPU里单精度和双精度的浮点计算能力需要分开计算,以最新的Tesla P100为例: 双精度理论峰值 = FP64 Cores *…...

js:获取浏览器默认语言
实现代码 navigator.language zh-CN参考文章 [javascript] js如何获取浏览器的语言...
【U8+】用友U8重新注册加密锁,提示:写卡失败,请重新配置客户端控件。
【问题描述】 用友U8软件重新安装后,需要重新注册加密锁激活软件。 注册反馈提示:产品注册失败。 原因(1):写卡失败,请重新配置客户端控件。 【解决方法】 1、打开控制面板,网络和 Internet&a…...

uniapp小程序console.log在微信开发者工具中不打印问题
最近在开发一款uniapp小程序,发现console.log在微信开发者工具中不打印,但在H5页面就能够有打印输出,于是在网上寻找原因… 主要是由于vue.config.js文件中有设置发布时删除console的配置,如下: 官网参考地址&#x…...
从零基础开始开发自己的第一个微信小程序
文章目录 内容介绍小程序开发步骤注册微信小程序账号下载开发工具搭建开发环境创建工程编写代码手机上查看效果 工程里的文件作用介绍总结 内容介绍 通过本篇blog,你可以熟悉从零开始,搭建小程序开发环境,并运行起自己的第一个小程序。 小程…...

无涯教程-Lua - Arrays(数组)
数组是对象的有序排列,可以是包含行集合的一维数组,也可以是包含多行和多列的多维数组。 在Lua中,数组是使用带有整数的索引表实现的。数组的大小不是固定的,并且可以根据无涯教程的要求(取决于内存限制)来增长。 一维数组 一维…...
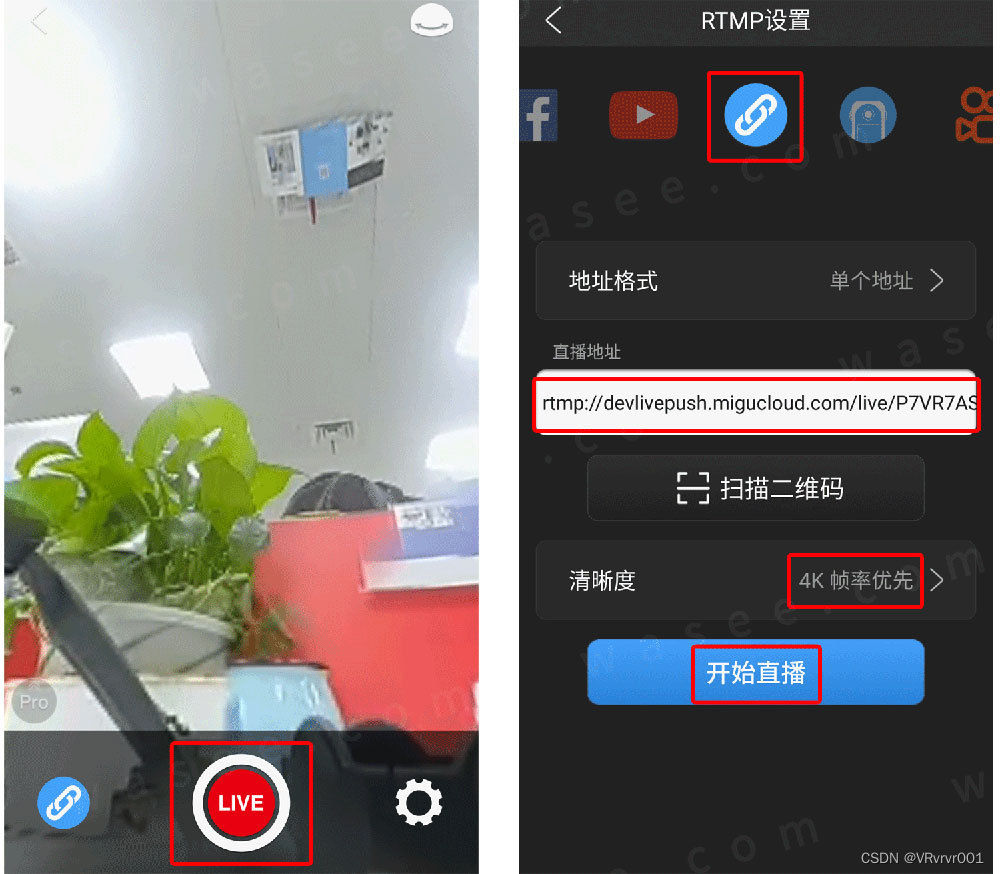
0基础学习VR全景平台篇 第76篇:全景相机-圆周率全景相机如何直播推流
圆周率科技,成立于2012年,是中国最早投身嵌入式全景算法研发的团队之一,亦是全球市场占有率最大的全景算法供应商。相继推出一体化智能屏、支持一键高清全景直播的智慧全景相机--Pilot Era和Pilot One,为用户带来实时畅享8K的高清…...
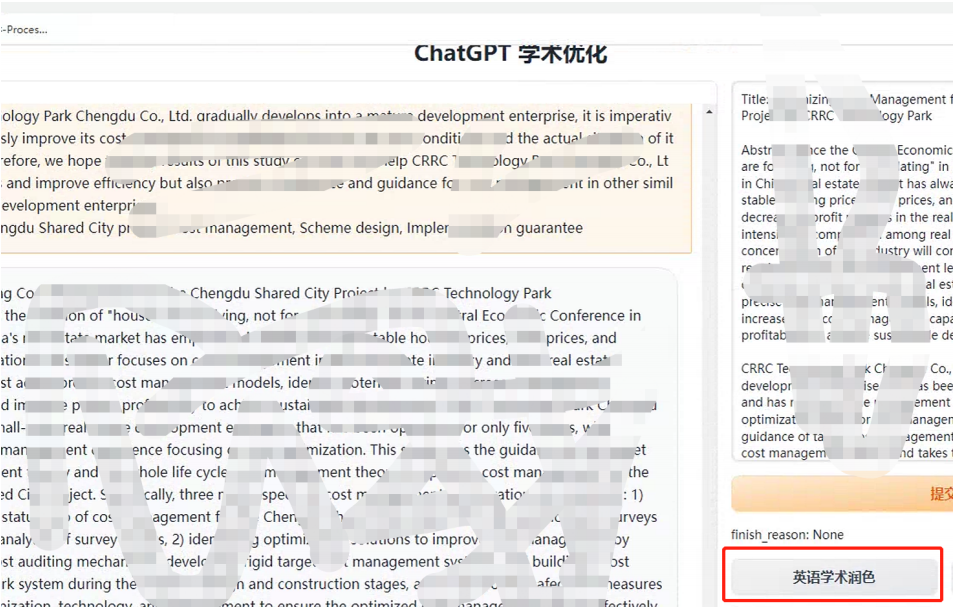
超详细|ChatGPT论文润色教程
本文讲述使用中科大开源ChatGPT论文辅助工具,对论文进行润色 祝看到本教程的小伙伴们都完成论文,顺利毕业。 可以加QQ群交流,一群: 123589938 第一章 介绍 今天给大家分享一款非常不错的ChatGPT论文辅助工具,使用了专…...
MMDeploy安装、python API测试及C++推理
服务器配置如下: Cuda版本:11.1 Cudnn版本:8.2.0 显卡版本:RTX3090 使用转换脚本将.pth模型转换为ONNX格式 python mmdeploy/tools/deploy.py \mmdeploy/configs/mmdet/detection/detection_onnxruntime_dynamic.py \mmdetect…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
