【3维视觉】3D空间常用算法(点到直线距离、面法线、二面角)
3D空间点到直线的距离
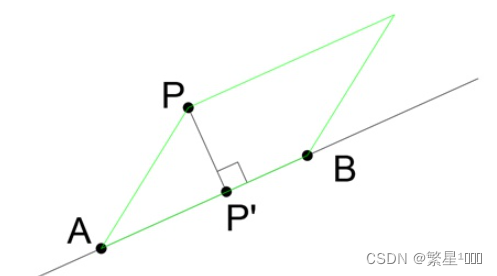
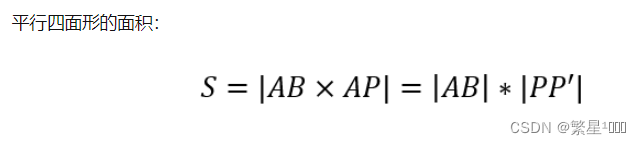
3D空间点到直线的距离
3D空间的曲率
三维空间有三个基本元素,点,线,面。那么曲率是如何定义的呢?
点的曲率?
线的曲率?
面的曲率?
法曲率
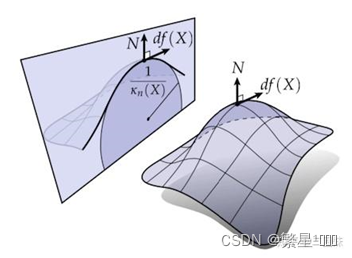
设曲面上的曲线在某一点处的切向量为df(X),曲面在这一点处的法向量为N。则曲线的法曲率就是曲线在df(X)和N张成的平面上的投影曲线的曲率。
在曲面上取一点E,曲面在E点的法线为z轴,过z轴可以有无限多个剖切平面,每个剖切平面与曲面相交,其交线为一条平面曲线,每条平面曲线在E点有一个曲率半径。不同的剖切平面上的平面曲线在E点的曲率半径一般是不相等的。
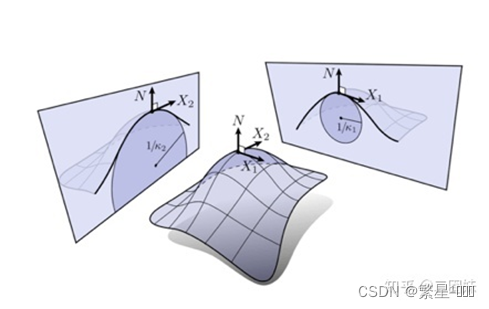
主曲率
曲面的每个方向都有法曲率,那么就有最大最小的法曲率,这个最大最小值就是主曲率,对应的曲线在这点的切线方向就是主曲率方向。这两个方向是垂直的。
根据主曲率的不同,可以对曲面分类
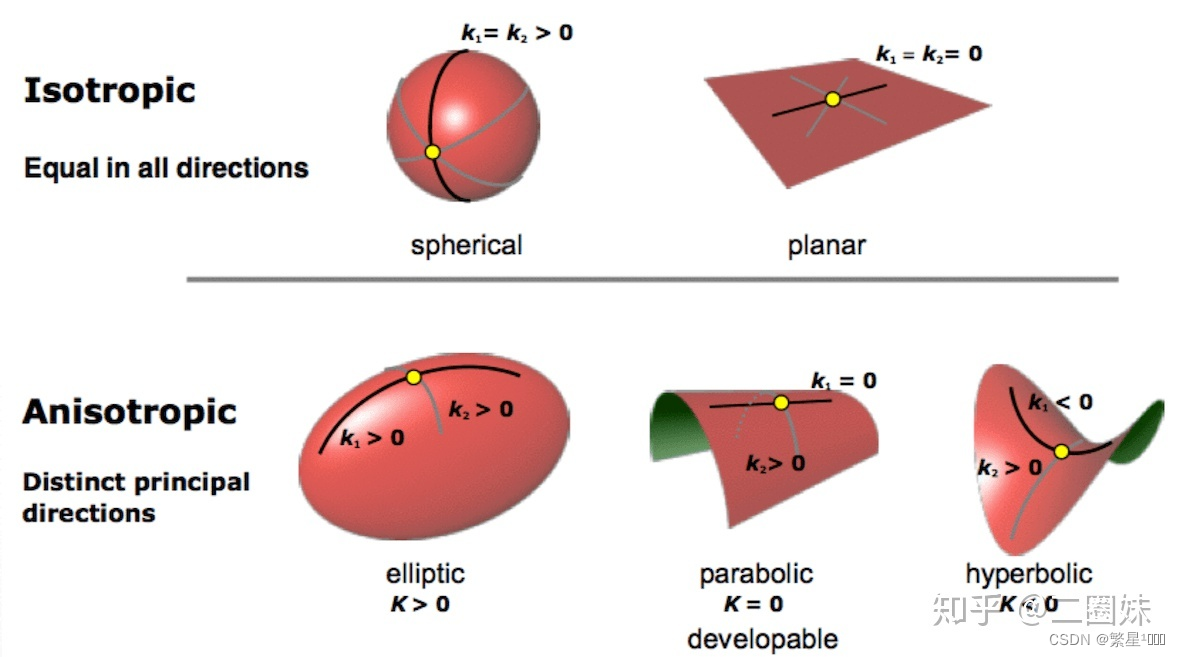
高斯曲率
微分几何中,曲面上一点的高斯曲率是该点主曲率κ1和κ2的乘积。
K = k 1 ∗ k 2 K= k_1*k_2 K=k1∗k2
**它是曲率的内在度量,度量的是曲面内在的弯曲程度。**也即,它的值只依赖于曲面上的距离如何测量,而不是曲面如何嵌入到空间。一个曲面做任何非拉伸的变换都不会改变它的高斯曲率,如平面高斯曲率为0,把它弯曲成圆柱,其高斯曲率也还是为0。
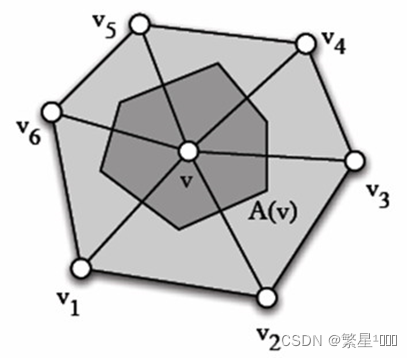
三维网格高斯曲率计算公式:
K ( v ) = 1 A ( v ) ( 2 π − ∑ v i ∈ N 1 ( v ) θ i ) K(v) = \frac{1}{A(v)}(2\pi - \sum_{v_i\in{ N_1}(v)}\theta_i) K(v)=A(v)1(2π−vi∈N1(v)∑θi)
这个公式的几何意义是比较直观的,2*Pi-该点邻域三角形对应的角度和,再除以相应区域的面积,就刻画了该点曲面的弯曲程度。
平均曲率
微分几何中,曲面上一点的平均曲率是该点主曲率κ1和κ2的平均值。
K = k 1 + k 2 2 K=\frac{k_1 + k_2}{2} K=2k1+k2
它度量了曲面在空间中的弯曲程度。比如平面弯曲成圆柱后,其平均曲率就不为0了。
高斯曲率
如何简明地解释曲率(curvature)?
法曲率、主曲率、高斯曲率、平均曲率
三角网格表面高斯曲率的计算与可视化
相关文章:

【3维视觉】3D空间常用算法(点到直线距离、面法线、二面角)
3D空间点到直线的距离 3D空间点到直线的距离 3D空间的曲率 三维空间有三个基本元素,点,线,面。那么曲率是如何定义的呢? 点的曲率? 线的曲率? 面的曲率? 法曲率 设曲面上的曲线在某一点处的切…...
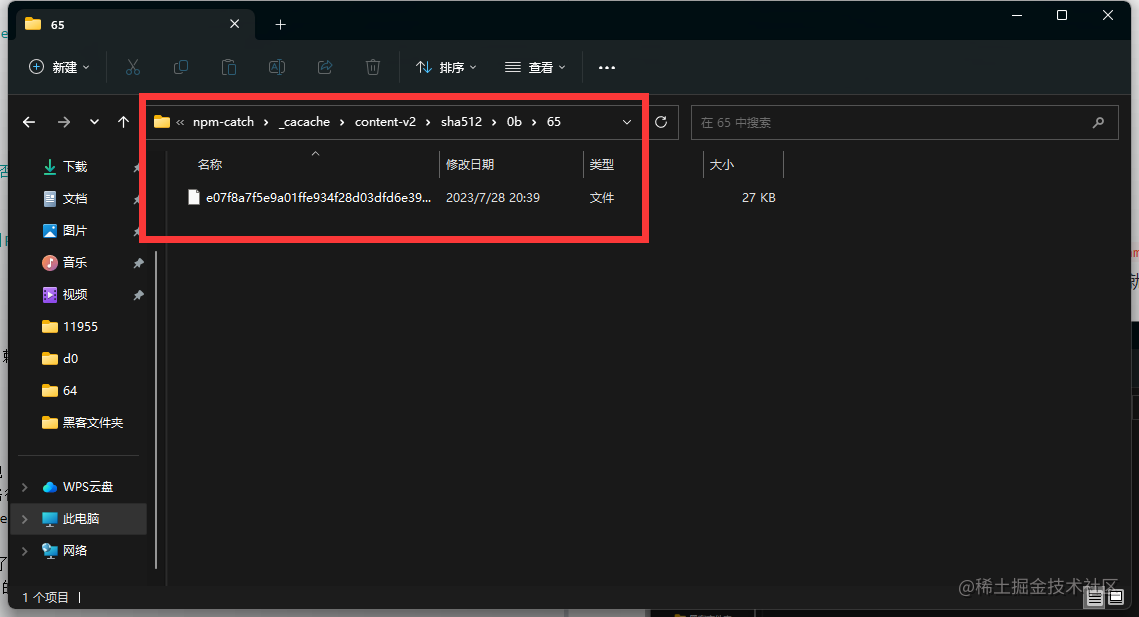
Nodejs 第四章(Npm install 原理)
在执行npm install 的时候发生了什么? 首先安装的依赖都会存放在根目录的node_modules,默认采用扁平化的方式安装,并且排序规则.bin第一个然后系列,再然后按照首字母排序abcd等,并且使用的算法是广度优先遍历,在遍历依…...
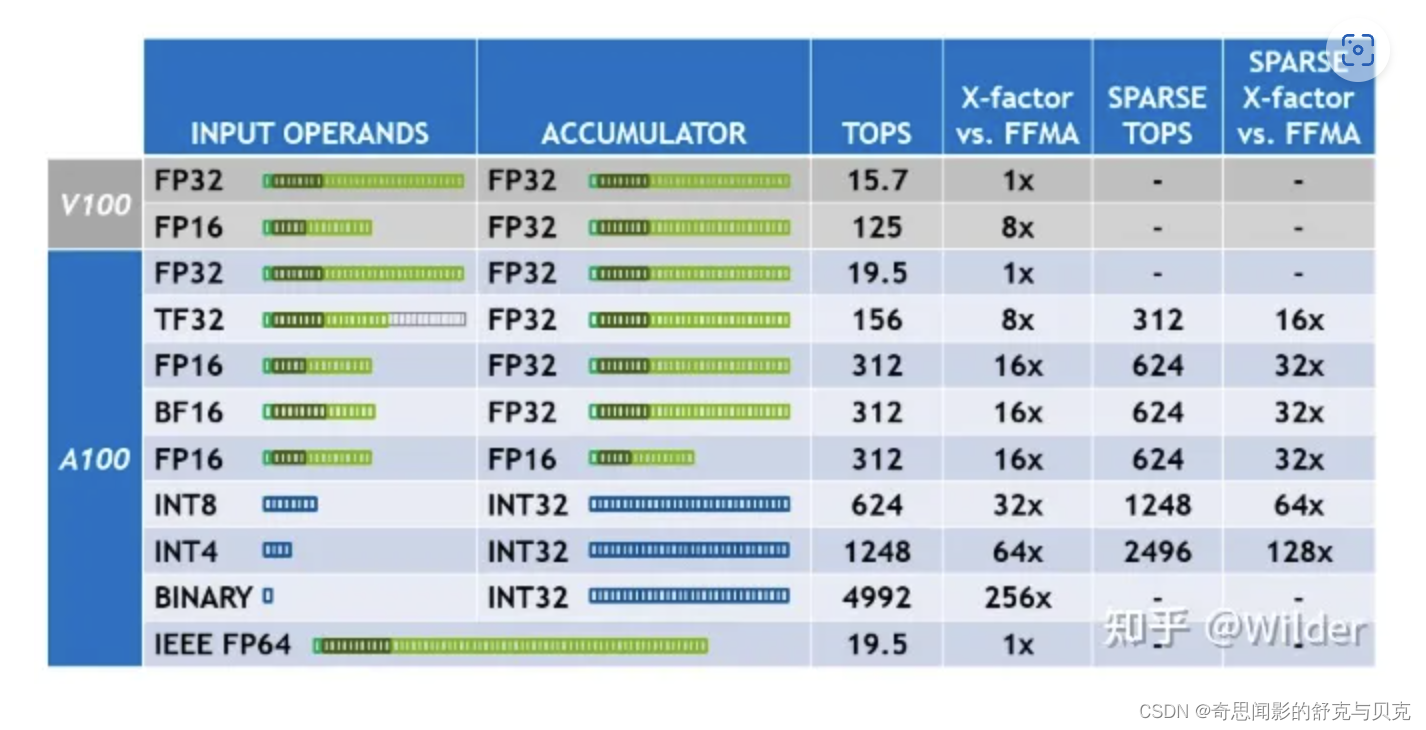
[深度学习] GPU处理能力(TFLOPS/TOPS)
计算能力换算 理论峰值 = GPU芯片数量GPU Boost主频核心数量*单个时钟周期内能处理的浮点计算次数 只不过在GPU里单精度和双精度的浮点计算能力需要分开计算,以最新的Tesla P100为例: 双精度理论峰值 = FP64 Cores *…...

js:获取浏览器默认语言
实现代码 navigator.language zh-CN参考文章 [javascript] js如何获取浏览器的语言...
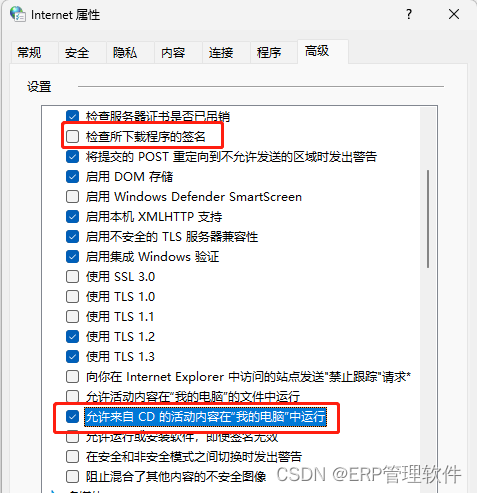
【U8+】用友U8重新注册加密锁,提示:写卡失败,请重新配置客户端控件。
【问题描述】 用友U8软件重新安装后,需要重新注册加密锁激活软件。 注册反馈提示:产品注册失败。 原因(1):写卡失败,请重新配置客户端控件。 【解决方法】 1、打开控制面板,网络和 Internet&a…...

uniapp小程序console.log在微信开发者工具中不打印问题
最近在开发一款uniapp小程序,发现console.log在微信开发者工具中不打印,但在H5页面就能够有打印输出,于是在网上寻找原因… 主要是由于vue.config.js文件中有设置发布时删除console的配置,如下: 官网参考地址&#x…...
从零基础开始开发自己的第一个微信小程序
文章目录 内容介绍小程序开发步骤注册微信小程序账号下载开发工具搭建开发环境创建工程编写代码手机上查看效果 工程里的文件作用介绍总结 内容介绍 通过本篇blog,你可以熟悉从零开始,搭建小程序开发环境,并运行起自己的第一个小程序。 小程…...

无涯教程-Lua - Arrays(数组)
数组是对象的有序排列,可以是包含行集合的一维数组,也可以是包含多行和多列的多维数组。 在Lua中,数组是使用带有整数的索引表实现的。数组的大小不是固定的,并且可以根据无涯教程的要求(取决于内存限制)来增长。 一维数组 一维…...
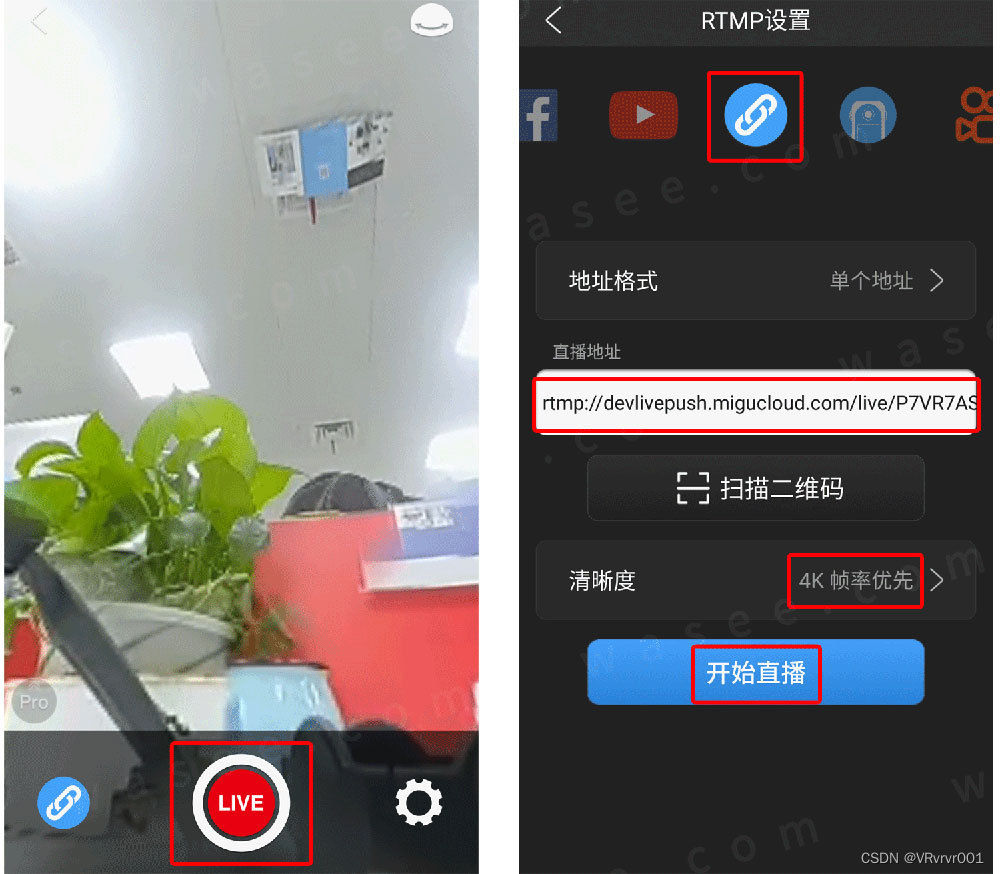
0基础学习VR全景平台篇 第76篇:全景相机-圆周率全景相机如何直播推流
圆周率科技,成立于2012年,是中国最早投身嵌入式全景算法研发的团队之一,亦是全球市场占有率最大的全景算法供应商。相继推出一体化智能屏、支持一键高清全景直播的智慧全景相机--Pilot Era和Pilot One,为用户带来实时畅享8K的高清…...
超详细|ChatGPT论文润色教程
本文讲述使用中科大开源ChatGPT论文辅助工具,对论文进行润色 祝看到本教程的小伙伴们都完成论文,顺利毕业。 可以加QQ群交流,一群: 123589938 第一章 介绍 今天给大家分享一款非常不错的ChatGPT论文辅助工具,使用了专…...
MMDeploy安装、python API测试及C++推理
服务器配置如下: Cuda版本:11.1 Cudnn版本:8.2.0 显卡版本:RTX3090 使用转换脚本将.pth模型转换为ONNX格式 python mmdeploy/tools/deploy.py \mmdeploy/configs/mmdet/detection/detection_onnxruntime_dynamic.py \mmdetect…...
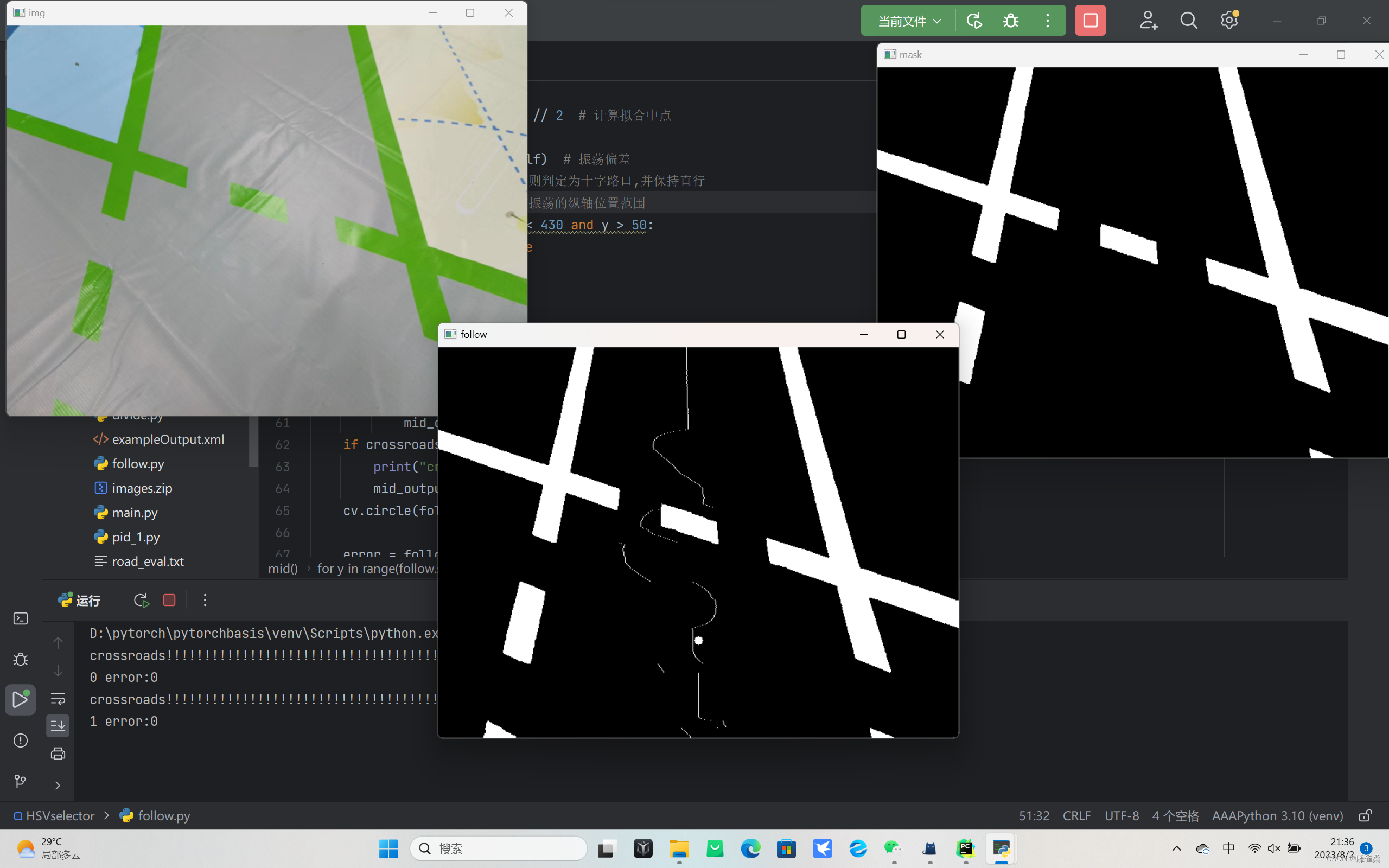
[openCV]基于拟合中线的智能车巡线方案V3
import cv2 as cv import os import numpy as np# 遍历文件夹函数 def getFileList(dir, Filelist, extNone):"""获取文件夹及其子文件夹中文件列表输入 dir:文件夹根目录输入 ext: 扩展名返回: 文件路径列表"""newDir d…...
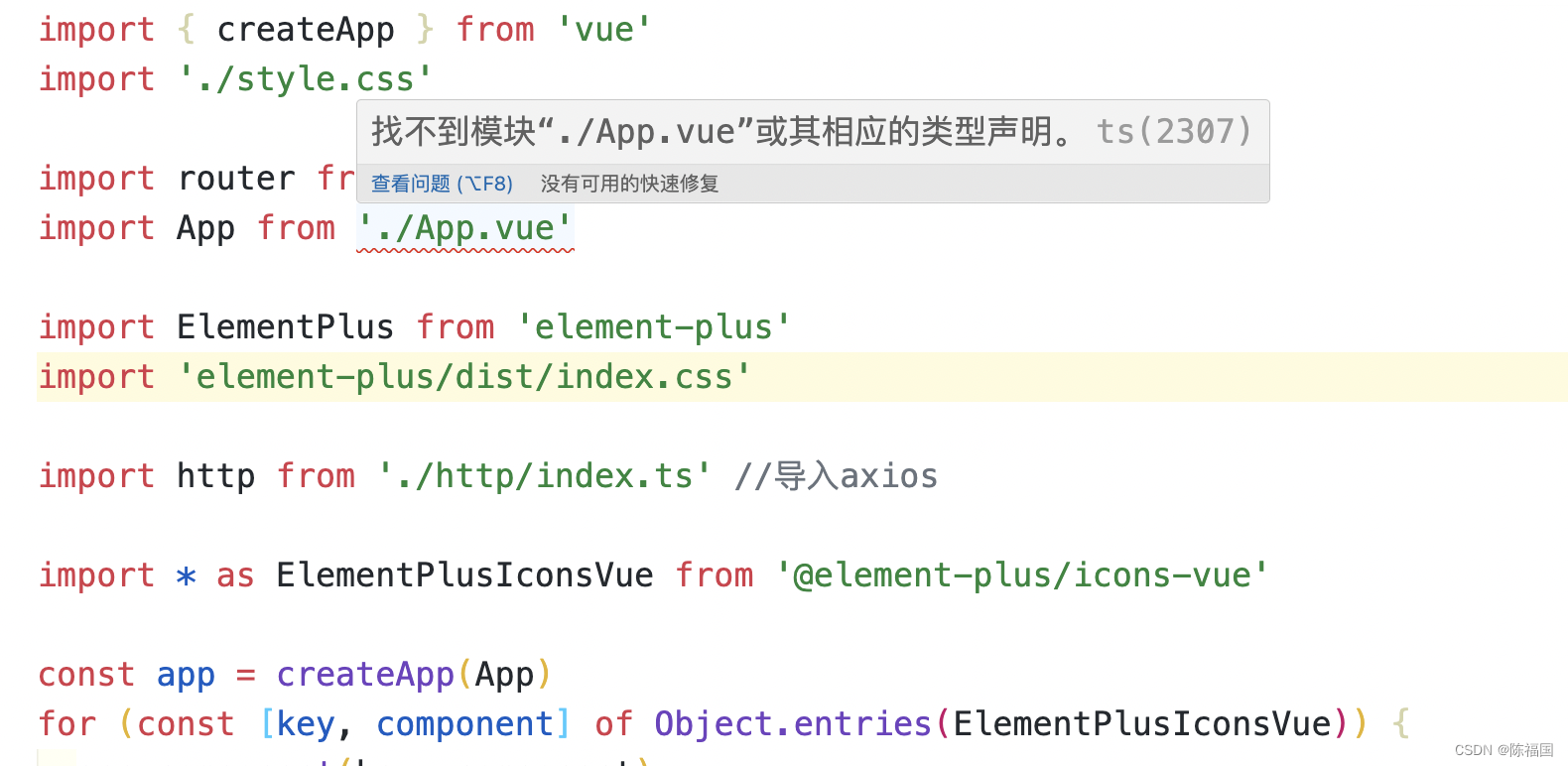
vite+typescript项目 :找不到模块“./***.vue”或其相应的类型声明——解决方案
vue3ts报错: 找不到模块“./App.vue”或其相应的类型声明。ts(2307) 解决方法: 1、在src文件夹找到 vite-env.d.ts 加入以下代码: declare module *.vue {import type { DefineComponent } from vueconst vueComponent: DefineComponent<…...
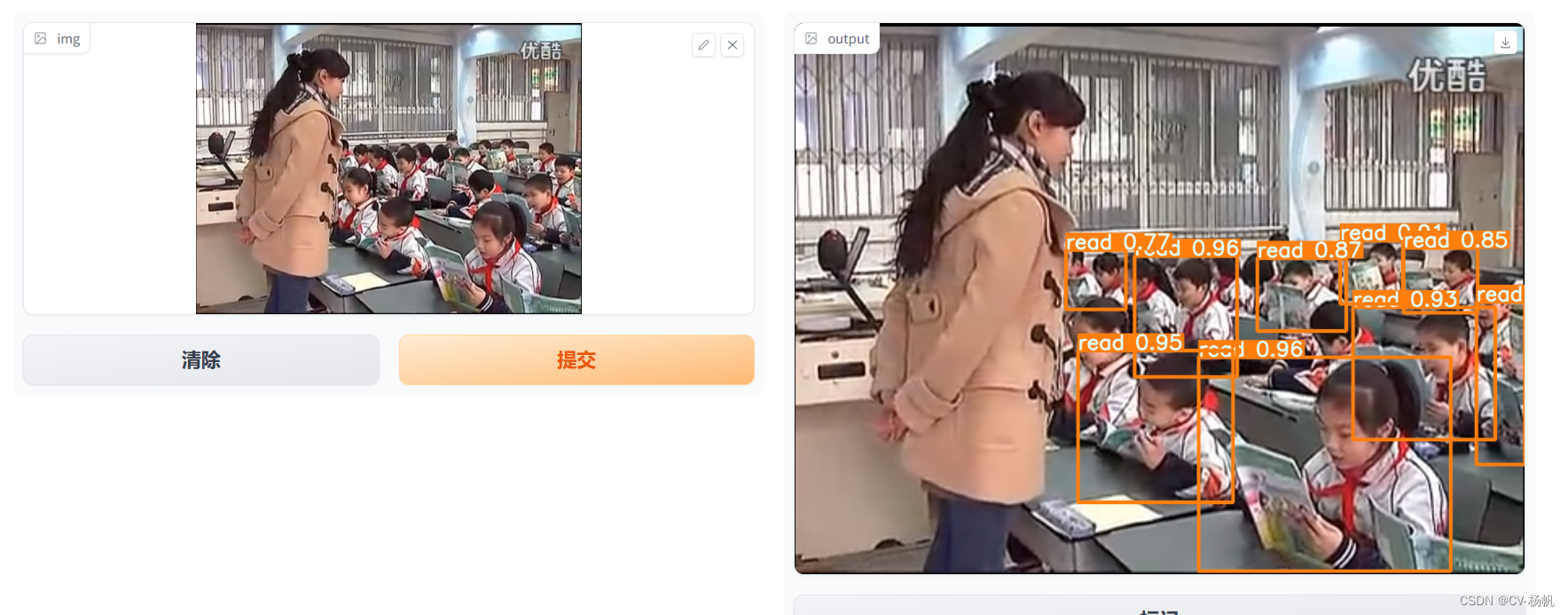
Gradio-YOLOv5-YOLOv7 搭建Web GUI
目录 0 相关资料:1 Gradio介绍2 环境搭建3 GradioYOLOv54 GradioYOLOv75 源码解释 0 相关资料: Gradio-YOLOv5-Det:https://gitee.com/CV_Lab/gradio_yolov5_det 【手把手带你实战YOLOv5-入门篇】YOLOv5 Gradio搭建Web GUI: https://www.bi…...

HTML模板生成word,pdf文档
1.获取html模板 public static void main(String[] args) {String htmlContent getHtmlFileContent(templateName,dataMap);String exportType "pdf";if (exportType.equals("pdf")){convertToPdf(htmlContent,filePath);}else {exportWord(htmlContent…...
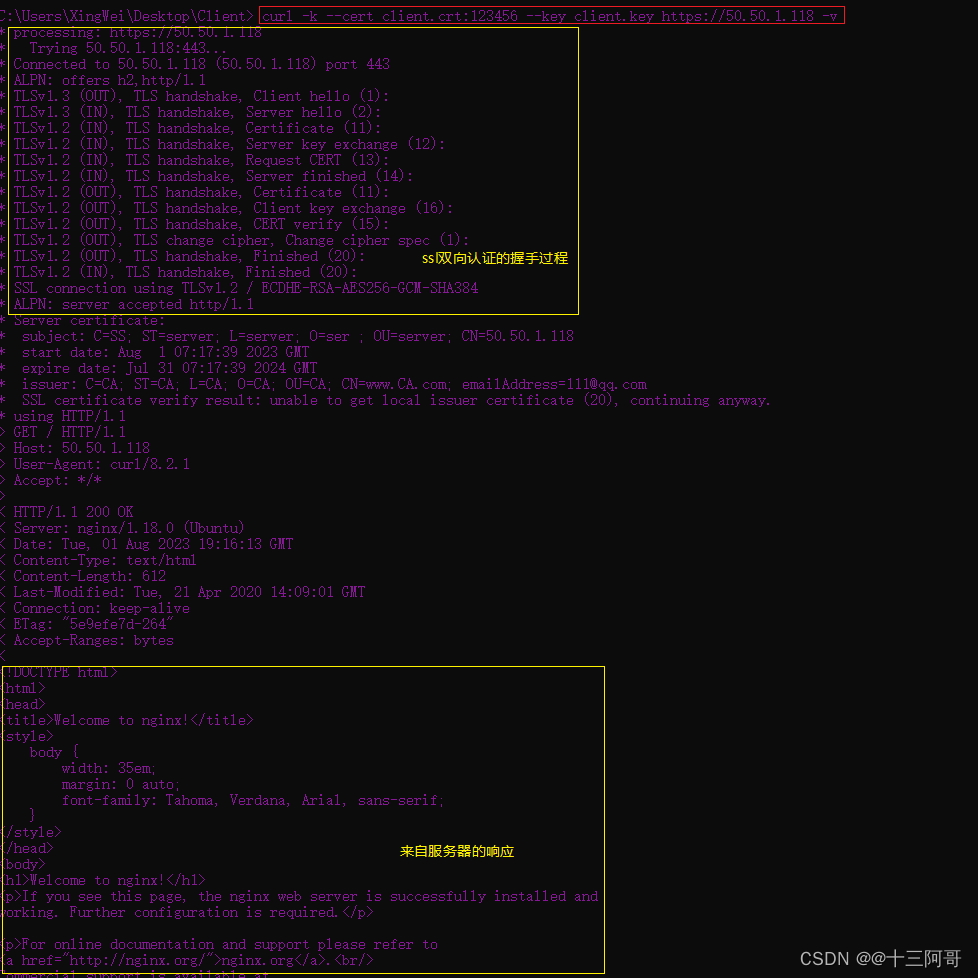
ssl单向证书和双向证书校验测试及搭建流程
零、前提准备 首先了解下HTTP和HTTPS的区别: HTTPS与HTTP有什么不同? HTTP是过去很长一段时间我们经常用到的一种传输协议。HTTP协议传输的数据都是未加密的,这就意味着用户填写的密码、账号、交易记录等机密信息都是明文,随时…...
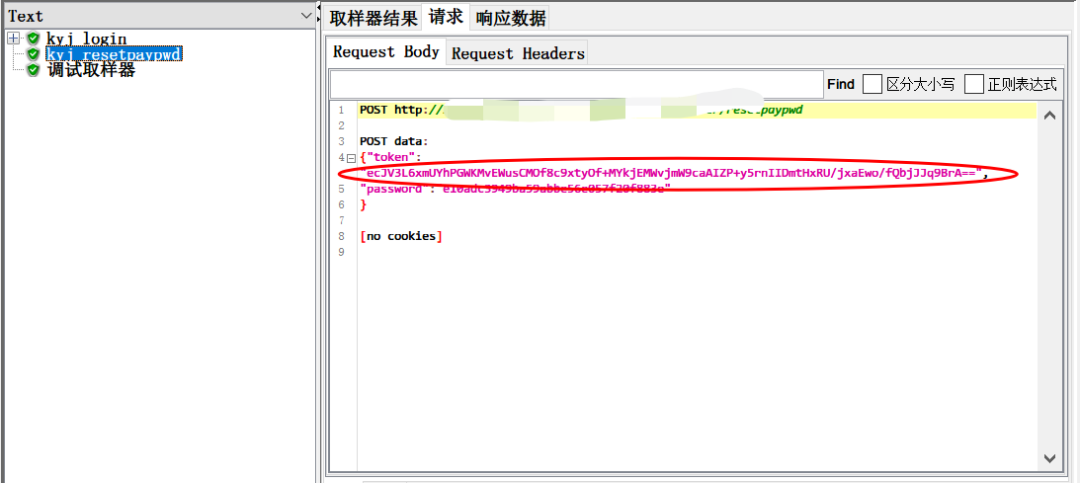
【2种方法,jmeter用一个正则提取器提取多个值!】
jmeter中,用json提取器,一次提取多个值,这个很多人都会。但是,用正则提取器一次提取多个,是否可以呢? 肯定,很多人都自信满满的说,可以!形如:token":&q…...

012-堆,结构体
012-堆,结构体 堆空间的申请和释放 堆空间特点? 栈空间的特点是,自动申请自动释放 堆空间由用户自己主动申请,主动释放 利用函数malloc进行堆空间的申请 利用函数free进行堆空间使用完毕后的释放 问题: 局部变量的存储空间在栈区; 全局变量的存储空…...

GDAL C++ API 学习之路 OGRGeometry 多边形类 OGRPolygon
OGRPolygon class OGRPolygon 是 OGR 几何图形库中的一个类,用于表示多边形的几何图形。它是一种封闭的多边形,由一个或多个外环(OGRLinearRing)和零个或多个内环(OGRLinearRing)组成。多边形是平…...

文件传输协议FTP与托管文件传输MFT有什么区别?
传输敏感数据是日常业务中不可或缺的一环。但是,在把敏感数据从A点搬到B点的过程中,保证该敏感数据的安全是组织的重要任务,因此最好选择一种能够确保文件安全的方案。 FTP与MFT有什么不同? FTP(文件传输协议…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...

Q1起重机指挥理论备考要点分析
Q1起重机指挥理论备考要点分析 一、考试重点内容概述 Q1起重机指挥理论考试主要包含三大核心模块:安全技术知识(占40%)、指挥信号规范(占30%)和法规标准(占30%)。考试采用百分制,8…...
个人电脑部署本地大模型+UI
在这个AI飞速进步的时代,越来越多的大模型出现在市面上 本地大模型也越来越火爆! 它完全免费,随时可以访问,数据仅存在本地,还可以自己微调,训练! 今天我来教大家,如何在一台普通…...
