机器学习知识经验分享之六:决策树
python语言用于深度学习较为广泛,R语言用于机器学习领域中的数据预测和数据处理算法较多,后续将更多分享机器学习数据预测相关知识的分享,有需要的朋友可持续关注,有疑问可以关注后私信留言。
目录
一、R语言介绍
二、R语言安装(Windows为例)
一、R语言介绍
R语言是一种自由、开源的编程语言和统计软件环境,在统计计算和图形绘制方面具有非常强的能力。R语言最初是由新西兰奥克兰大学的Ross Ihaka和Robert Gentleman开发的,现在它是由全球的统计学家和程序员共同发展维护。R语言支持多种统计方法,如线性和非线性建模、经典统计和计量经济学、时间序列分析、分类和聚类等。R语言也有一个非常强大的图形系统,能够生成各种高质量的统计图形。R语言的优点不仅体现在其免费和开源的特性上,还包括其强大的数据处理和可视化功能、与其他编程语言和数据格式的互操作性、自由开发的扩展包、社区支持和可移植性等。R语言大量的扩展包是它的一大特点,这些扩展包提供各种各样的扩展功能和工具,如机器学习、深度学习、自然语言处理和网络分析等。总之,R语言不仅是一种统计学家和数据科学家的工具,也是在更广泛的科学、工程和商业领域中广泛使用的高级编程语言。
二、R语言安装(Windows为例)
与python语言安装一样,1.可以先在R官网(https://www.r-project.org/)并下载最新的R for Windows安装程序。2. 运行下载的R for Windows安装程序,按照提示进行安装。默认情况下,R语言将被安装到C: \ Program Files \ R文件夹中。3. 安装程序可能会提示选择安装项,例如安装32位或64位版本、添加图形用户界面等。根据自己的需求进行选择。4. 等待安装程序完成,安装程序将创建R的快捷方式,可以通过启动菜单或桌面上的图标启动。然后,安装R语言的IDE——RStudio.RStudio IDE - RStudio
以下为R语言代码示例:
# 安装库
install.packages("dplyr")
# 加载所需的库
library(dplyr)# 读取csv文件
df <- read.csv("data.csv")# 数据清洗
df <- df %>% filter(!is.na(attr_1)) %>% select(-c(attr_2, attr_3))# 数据分组和统计
result <- df %>% group_by(attr_1) %>%summarise(count = n(), mean_val = mean(attr_4), max_val = max(attr_5))
该语句的功能包括以下几步:
1. 加载dplyr库,方便进行数据清洗、分组和统计操作。
2. 从csv文件中读取数据并存储到df数据框中。
3. 对df数据框进行数据清洗操作,将包含NA值的行删除,并删除不需要的列。
4. 对清洗后的df数据框进行分组操作,并统计各组数据数量、attr_4的平均值和attr_5的最大值。
5. 最终结果存储在result数据框中。
三、R语言书籍分享
有需要的朋友关注后私信获取。
百度网盘链接:https://pan.baidu.com/s/1hFIjbbk6h8uQVmATX5O_AQ
提取码:关注后私信获取



四、R语言运行常见报错
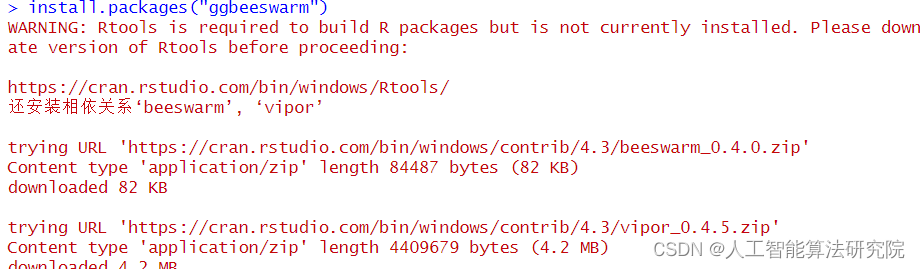
常见报错:Error in loadNamespace(x) : 不存在叫‘ggbeeswarm’这个名字的程辑包

错误原因:R语言跟python语言一样也有大量的库,这种就是缺少库的原因。
解决方法:install.packages("ggbeeswarm")
后续将持续分享决策树、随机森林、回归网络等用R语言来实现的机器学习算法的讲解,有需要的朋友请持续关注,有疑问可以关注后私信留言。
相关文章:

机器学习知识经验分享之六:决策树
python语言用于深度学习较为广泛,R语言用于机器学习领域中的数据预测和数据处理算法较多,后续将更多分享机器学习数据预测相关知识的分享,有需要的朋友可持续关注,有疑问可以关注后私信留言。 目录 一、R语言介绍 二、R语言安装…...

回归预测 | MATLAB实现SO-CNN-GRU蛇群算法优化卷积门控循环单元多输入单输出回归预测
回归预测 | MATLAB实现SO-CNN-GRU蛇群算法优化卷积门控循环单元多输入单输出回归预测 目录 回归预测 | MATLAB实现SO-CNN-GRU蛇群算法优化卷积门控循环单元多输入单输出回归预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现SO-CNN-GRU蛇群算法优化卷积门控循…...

309. 买卖股票的最佳时机含冷冻期
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。 设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票): 卖出股票后,你无法在第二天买入股票 …...

P1119 灾后重建
题目背景 B 地区在地震过后,所有村庄都造成了一定的损毁,而这场地震却没对公路造成什么影响。但是在村庄重建好之前,所有与未重建完成的村庄的公路均无法通车。换句话说,只有连接着两个重建完成的村庄的公路才能通车,…...

USB采集卡如何打pts
一、使用采集卡提供的pts 二、手动打pts 1.usb采集设备pts的问题 2.采集卡驱动,UVC/UAC,ffmpeg的关系 3.如何自己打pts 4.音视频同步调优 5.NTP等联网调时工具带来的不同步问题 一、使用采集卡提供的pts 我们用使用pc摄像头和使用pc麦克风声卡里的方法&…...
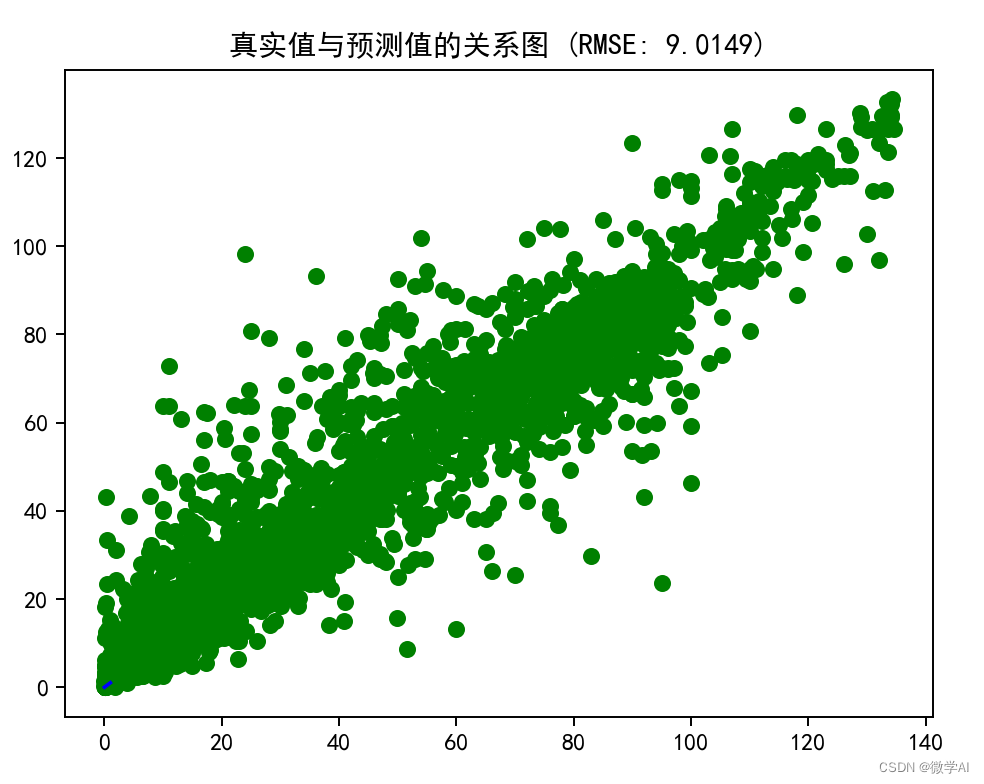
机器学习实战13-超导体材料的临界温度预测与分析(决策树回归,梯度提升回归,随机森林回归和Bagging回归)
大家好,我是微学AI,今天给大家介绍一下机器学习实战13-超导体材料的临界温度预测与分析(决策树回归,梯度提升回归,随机森林回归和Bagging回归),这几天引爆网络的科技大新闻就是韩国科研团队宣称发现了室温超导材料-LK-99,这种材料…...

小研究 - 一种复杂微服务系统异常行为分析与定位算法(二)
针对极端学生化偏差(Extreme Studentized &#…...

Docker 安装 MySQL5.6
方法一、docker pull mysql 查找Docker Hub上的mysql镜像 #docker search mysql 这里我们拉取官方的镜像,标签为5.6 #docker pull mysql:5.6 (第一次启动Docker-MySql主要是查看Docker里面MySQL的默认配置,数据位置,日志位置,配…...
)
vue组件跳层级时的事件处理 (事件的广播与派发)
相信大家一定用过elementui这个组件库,那么对里面的表单组件一定不陌生。 最常用的几个组件就是el-form,el-form-item,el-input,表单校验时的错误提示功能是交给el-form-item来实现的。当el-input填写时触发校验规则,…...
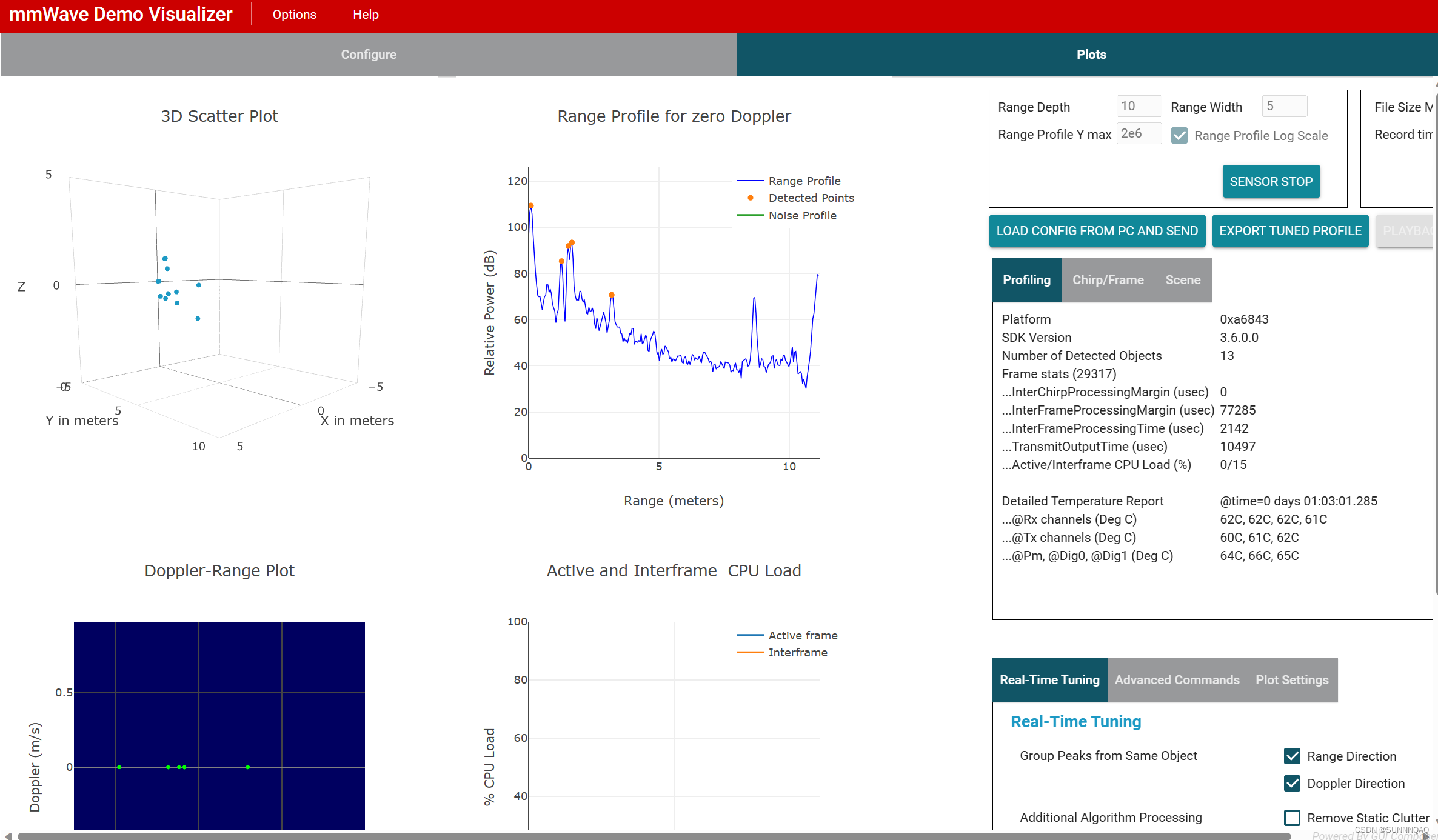
毫米波雷达 TI IWR6843 官方测试程序(Out Of Box Demo)
1.硬件准备 1.IWR6843AOP板子 2.两个USB转串口模块(因为我的是自己做的板子,板子上没有集成USB转串口芯片) 2.软件准备 1.最新版本的CCS,注意后缀没有THEIA https://www.ti.com/tool/CCSTUDIO?DCMPdsp_ccs_v4&HQSccs 2.最…...

中大标了 5813万
汗水浇灌收获,实干笃定前行。刚刚进入八月,鸿雁政企事业部就传来了特大喜讯——鸿雁中标浙江丽水国际会展中心电线电缆项目,中标总金额达5813万!一举刷新鸿雁单体项目中最高中标金额。 据了解,浙江丽水国际会展中心项…...

Java电子招投标采购系统源码-适合于招标代理、政府采购、企业采购、等业务的企业 tbms
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查…...
RocketMQ安装和简单使用
说明:RocketMQ与RabbitMQ一样,是分布式架构中的一个组件,用来解决微服务之间的异步调用。同类的还有两个,各自的特点如下: Rocket结构 服务启动时 发送消息时 其中各个部分的功能如下: (1&…...
Codeforces Round 869 (Div. 2)
C 求最长似递增子序列 是子序列! 我误以为是最长上升子序列的变式,但是这个题目和那个题目,并不是很一样 我们选择观察样例: 1 2 4 3 3 5 6 2 1 其实样例当中就给我们了答案,我们能感觉的出来,应该是用长…...

【雕爷学编程】MicroPython动手做(28)——物联网之Yeelight 3
知识点:什么是掌控板? 掌控板是一块普及STEAM创客教育、人工智能教育、机器人编程教育的开源智能硬件。它集成ESP-32高性能双核芯片,支持WiFi和蓝牙双模通信,可作为物联网节点,实现物联网应用。同时掌控板上集成了OLED…...
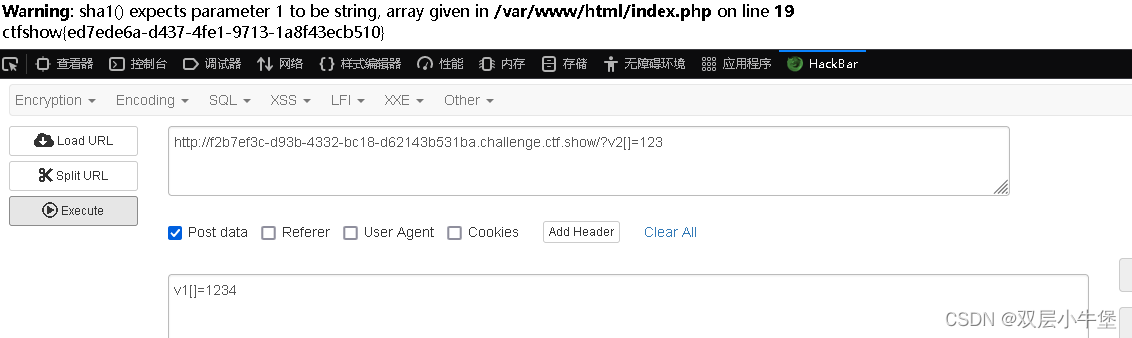
CTFSHOW php 特性
web89 数组绕过正则 include("flag.php"); highlight_file(__FILE__);if(isset($_GET[num])){$num $_GET[num]; get numif(preg_match("/[0-9]/", $num)){ 是数字 就输出 nodie("no no no!");}if(intval($num)){ 如果是存在整数 输出 flagecho …...
的排序)
2、认识O(nlogn)的排序
归并排序 分两半,谁小拷贝谁 public class Test{public static void mergeSort(int[] arr) {if (arr == null || arr.length < 2) {return;}mergeSort(arr, 0, arr.length - 1);}public static void mergeSort(int[] arr, int l, int r) {if (l == r) {return;}int mid =…...

什么是 HTTP 长轮询?
什么是 HTTP 长轮询? Web 应用程序最初是围绕客户端/服务器模型开发的,其中 Web 客户端始终是事务的发起者,向服务器请求数据。因此,没有任何机制可以让服务器在没有客户端先发出请求的情况下独立地向客户端发送或推送数据。 为…...

操作系统用户态和核心态和CPU上下文切换
目录 操作系统用户态和核心态用户态和核心态操作系统用户态和核心态是如何交换的系统调用 CPU上下文什么是CPU上下文和CPU上下文切换CPU为什么要进行上下文切换 操作系统用户态和核心态 用户态和核心态 操作系统两种状态:用户态和内核态。 操作系统的用户态和内核态…...
TSINGSEE青犀视频汇聚平台EasyCVR视频广场面包屑侧边栏支持拖拽操作
TSINGSEE青犀视频汇聚平台EasyCVR可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有GB28181、RTSP/Onvif、RTMP等,以及厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等,能对外分发RTSP、RTMP、FLV、HLS、Web…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
