P1119 灾后重建
题目背景
B 地区在地震过后,所有村庄都造成了一定的损毁,而这场地震却没对公路造成什么影响。但是在村庄重建好之前,所有与未重建完成的村庄的公路均无法通车。换句话说,只有连接着两个重建完成的村庄的公路才能通车,只能到达重建完成的村庄。
题目描述
给出 B 地区的村庄数 N,村庄编号从 0 到 N−1,和所有 M 条公路的长度,公路是双向的。并给出第 i 个村庄重建完成的时间 ti,你可以认为是同时开始重建并在第 ti 天重建完成,并且在当天即可通车。若 ti 为 0 则说明地震未对此地区造成损坏,一开始就可以通车。之后有 Q 个询问 (x,y,t),对于每个询问你要回答在第 t 天,从村庄 x 到村庄 y 的最短路径长度为多少。如果无法找到从 x 村庄到 y 村庄的路径,经过若干个已重建完成的村庄,或者村庄 x 或村庄 y 在第 t 天仍未重建完成,则需要输出 −1。
输入格式
第一行包含两个正整数 N,M,表示了村庄的数目与公路的数量。
第二行包含 N 个非负整数 t0,t1,⋯,tN−1,表示了每个村庄重建完成的时间,数据保证了 t0≤t1≤⋯≤tN−1。
接下来 M 行,每行 3 个非负整数 i,j,w,w 为不超过 10000 的正整数,表示了有一条连接村庄 i 与村庄 j 的道路,长度为 w,保证 j≠i,且对于任意一对村庄只会存在一条道路。
接下来一行也就是 M+3 行包含一个正整数 Q,表示 Q 个询问。
接下来 Q 行,每行 3 个非负整数 x,y,t,询问在第 t 天,从村庄 x 到村庄 y 的最短路径长度为多少,数据保证了 t 是不下降的。
输出格式
共Q 行,对每一个询问 (x,y,t) 输出对应的答案,即在第 t 天,从村庄 x 到村庄 y 的最短路径长度为多少。如果在第 t 天无法找到从 x 村庄到 y 村庄的路径,经过若干个已重建完成的村庄,或者村庄 x 或村庄 y 在第 t 天仍未修复完成,则输出 −1。
输入输出样例
输入 #1复制
4 5 1 2 3 4 0 2 1 2 3 1 3 1 2 2 1 4 0 3 5 4 2 0 2 0 1 2 0 1 3 0 1 4
输出 #1复制
-1 -1 5 4
说明/提示
- 对于 30% 的数据,有 N≤50;
- 对于 30% 的数据,有 ti=0,其中有 20% 的数据有 ti=0 且 N>50;
- 对于 50% 的数据,有 Q≤100;
- 对于 100% 的数据,有 1≤N≤200,20≤M≤2N×(N−1),1≤Q≤50000,所有输入数据涉及整数均不超过 105。
解析:
这题一看就是图论的问题,阅读完题目后村庄的修建时间是不减递增的。后面的询问时间也是递增的。
在联想到最短路问题有Floyd算法可以很快的求出最短路径,其数据也没有那么大。
这是一道不错的Floyd算法的运用。
普通的Floyd算法是三层for循环,dp[i][j] = min(dp[i][k],dp[k][j],dp[i][j]);
for(k=1;k<=n;k++)for(i=1;i<=n;i++)for(j=1;j<=n;j++)if(e[i][j]>e[i][k]+e[k][j])e[i][j]=e[i][k]+e[k][j];从i地点到k,在从k到达j。
所有的边全部给出,按照时间顺序更新每一个可用的点(即修建好村庄),对于每个时间点进行两点之间询问,求对于目前建设的所有村庄来说任意两点之间的最短路
不正好就是Floyd算法中使用前k个节点更新最短路的思维吗?
核心代码:
inline void updata(int k){ //以k为中心的点进行更新for(int i = 0;i <n;i++){for(int j = 0;j < n;j++){if(f[i][j] > f[i][k] + f[j][k]){f[i][j] = f[j][i] = f[i][k] + f[k][j];}}}return;
}代码:
#include<bits/stdc++.h>
using namespace std;
#define N 205
#define endl '\n'
int n,m;
int a[N];
int f[N][N];
inline void updata(int k){for(int i = 0;i <n;i++){for(int j = 0;j < n;j++){if(f[i][j] > f[i][k] + f[j][k]){f[i][j] = f[j][i] = f[i][k] + f[k][j];}}}return;
}
int main()
{cin >>n >> m;for(int i = 0;i < n;i++){scanf("%d",a+i);}for(int i = 0;i < n;i++){ //初始化 for(int j = 0;j < n;j++){f[i][j] = 1e9;}}for(int i = 0;i < n;i++) {f[i][i] = 0;}int s1,s2,s3;for(int i = 1;i <= m;i++){ //从s1 - s2 的距离 scanf("%d%d%d",&s1,&s2,&s3);f[s1][s2] = f[s2][s1] = s3;}int q;cin >> q;int now = 0;for(int i = 1;i <= q;i++){scanf("%d%d%d",&s1,&s2,&s3);while(a[now] <= s3 && now < n){ //now是指遍历到那个节点 updata(now);now++;}if(a[s1] > s3||a[s2] > s3) cout << -1<<endl;else{if(f[s1][s2] ==1e9) cout << -1 <<endl;else cout <<f[s1][s2] <<endl;}}return 0;
}
//4 5
//1 3 3 4
//0 2 1
//2 3 1
//3 1 2
//2 1 4
//0 3 5
//4
//2 0 2
//0 1 2
//0 1 3
//0 1 4相关文章:

P1119 灾后重建
题目背景 B 地区在地震过后,所有村庄都造成了一定的损毁,而这场地震却没对公路造成什么影响。但是在村庄重建好之前,所有与未重建完成的村庄的公路均无法通车。换句话说,只有连接着两个重建完成的村庄的公路才能通车,…...

USB采集卡如何打pts
一、使用采集卡提供的pts 二、手动打pts 1.usb采集设备pts的问题 2.采集卡驱动,UVC/UAC,ffmpeg的关系 3.如何自己打pts 4.音视频同步调优 5.NTP等联网调时工具带来的不同步问题 一、使用采集卡提供的pts 我们用使用pc摄像头和使用pc麦克风声卡里的方法&…...
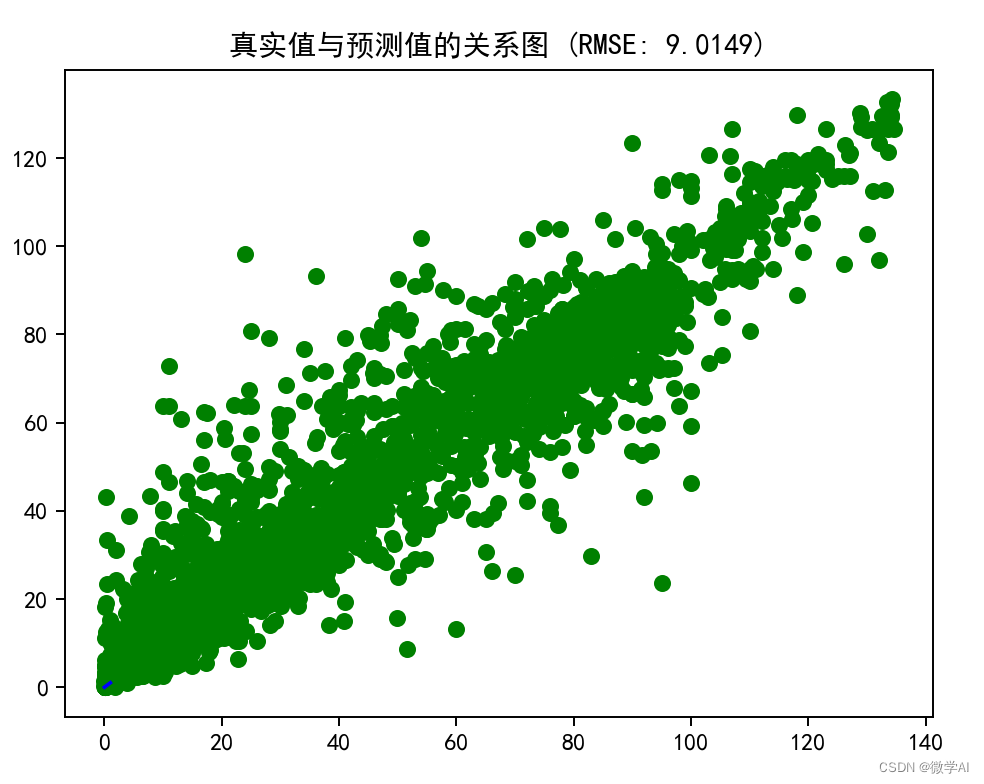
机器学习实战13-超导体材料的临界温度预测与分析(决策树回归,梯度提升回归,随机森林回归和Bagging回归)
大家好,我是微学AI,今天给大家介绍一下机器学习实战13-超导体材料的临界温度预测与分析(决策树回归,梯度提升回归,随机森林回归和Bagging回归),这几天引爆网络的科技大新闻就是韩国科研团队宣称发现了室温超导材料-LK-99,这种材料…...

小研究 - 一种复杂微服务系统异常行为分析与定位算法(二)
针对极端学生化偏差(Extreme Studentized &#…...

Docker 安装 MySQL5.6
方法一、docker pull mysql 查找Docker Hub上的mysql镜像 #docker search mysql 这里我们拉取官方的镜像,标签为5.6 #docker pull mysql:5.6 (第一次启动Docker-MySql主要是查看Docker里面MySQL的默认配置,数据位置,日志位置,配…...
)
vue组件跳层级时的事件处理 (事件的广播与派发)
相信大家一定用过elementui这个组件库,那么对里面的表单组件一定不陌生。 最常用的几个组件就是el-form,el-form-item,el-input,表单校验时的错误提示功能是交给el-form-item来实现的。当el-input填写时触发校验规则,…...
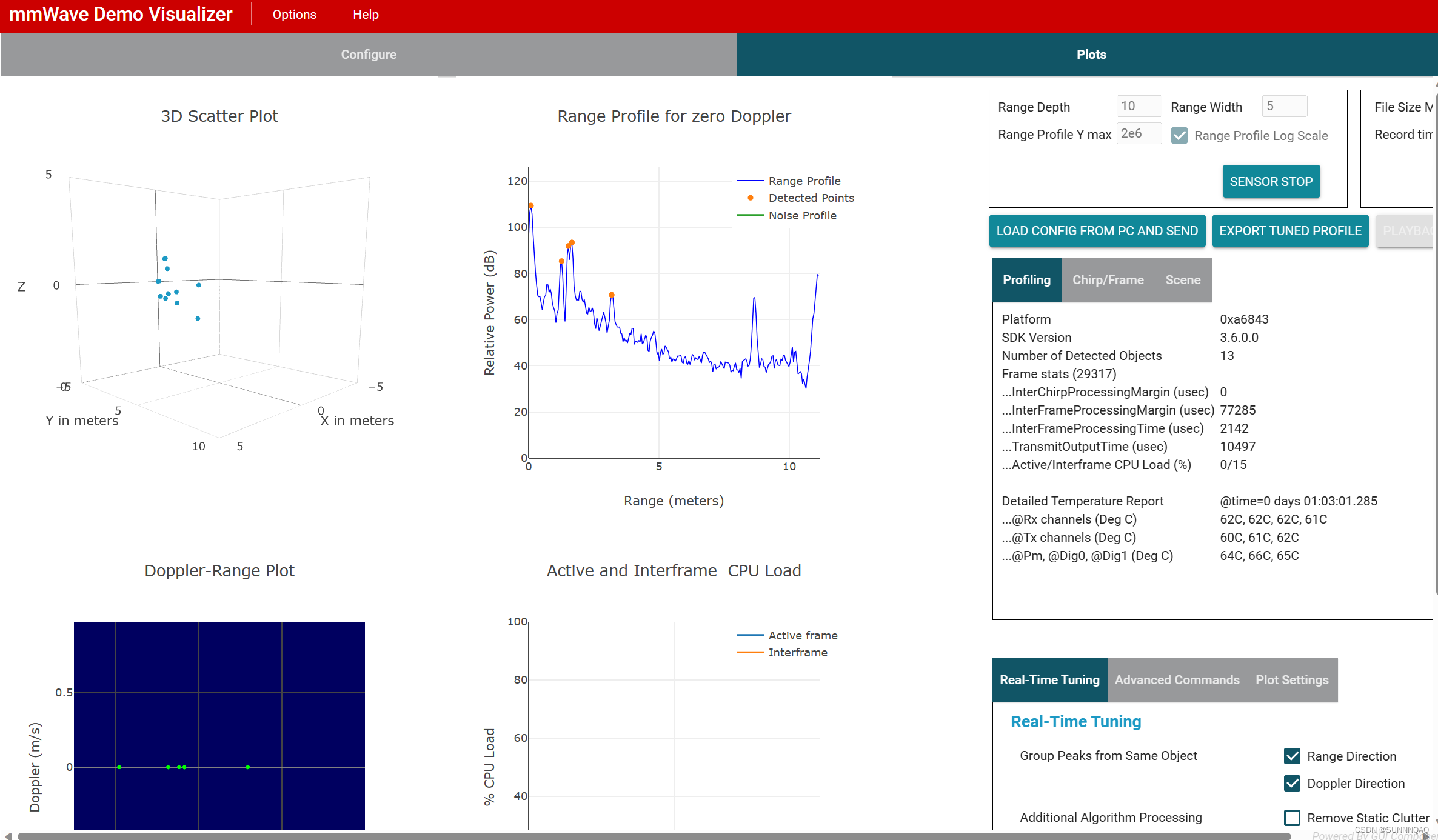
毫米波雷达 TI IWR6843 官方测试程序(Out Of Box Demo)
1.硬件准备 1.IWR6843AOP板子 2.两个USB转串口模块(因为我的是自己做的板子,板子上没有集成USB转串口芯片) 2.软件准备 1.最新版本的CCS,注意后缀没有THEIA https://www.ti.com/tool/CCSTUDIO?DCMPdsp_ccs_v4&HQSccs 2.最…...

中大标了 5813万
汗水浇灌收获,实干笃定前行。刚刚进入八月,鸿雁政企事业部就传来了特大喜讯——鸿雁中标浙江丽水国际会展中心电线电缆项目,中标总金额达5813万!一举刷新鸿雁单体项目中最高中标金额。 据了解,浙江丽水国际会展中心项…...

Java电子招投标采购系统源码-适合于招标代理、政府采购、企业采购、等业务的企业 tbms
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查…...
RocketMQ安装和简单使用
说明:RocketMQ与RabbitMQ一样,是分布式架构中的一个组件,用来解决微服务之间的异步调用。同类的还有两个,各自的特点如下: Rocket结构 服务启动时 发送消息时 其中各个部分的功能如下: (1&…...
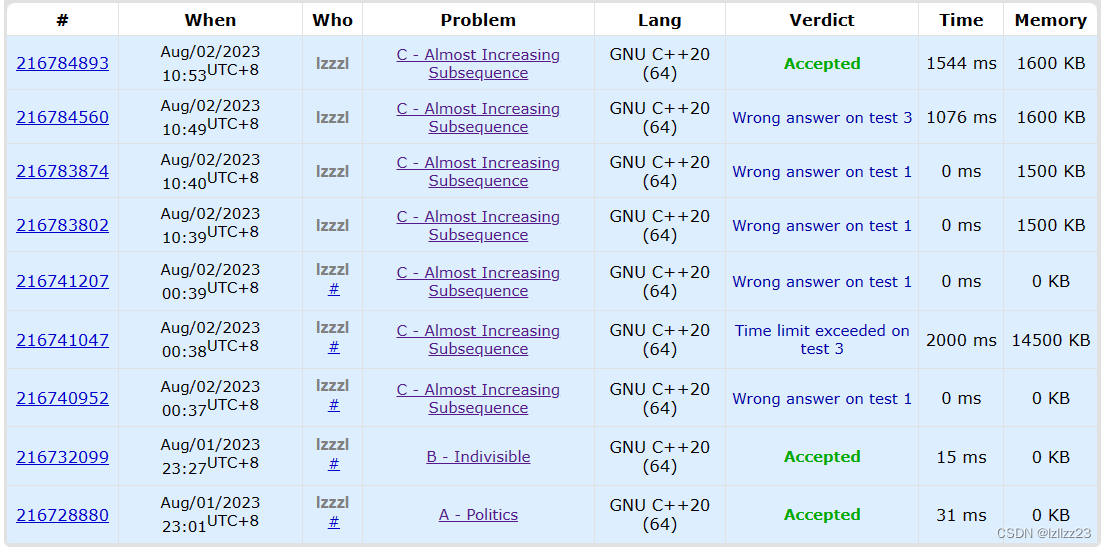
Codeforces Round 869 (Div. 2)
C 求最长似递增子序列 是子序列! 我误以为是最长上升子序列的变式,但是这个题目和那个题目,并不是很一样 我们选择观察样例: 1 2 4 3 3 5 6 2 1 其实样例当中就给我们了答案,我们能感觉的出来,应该是用长…...

【雕爷学编程】MicroPython动手做(28)——物联网之Yeelight 3
知识点:什么是掌控板? 掌控板是一块普及STEAM创客教育、人工智能教育、机器人编程教育的开源智能硬件。它集成ESP-32高性能双核芯片,支持WiFi和蓝牙双模通信,可作为物联网节点,实现物联网应用。同时掌控板上集成了OLED…...
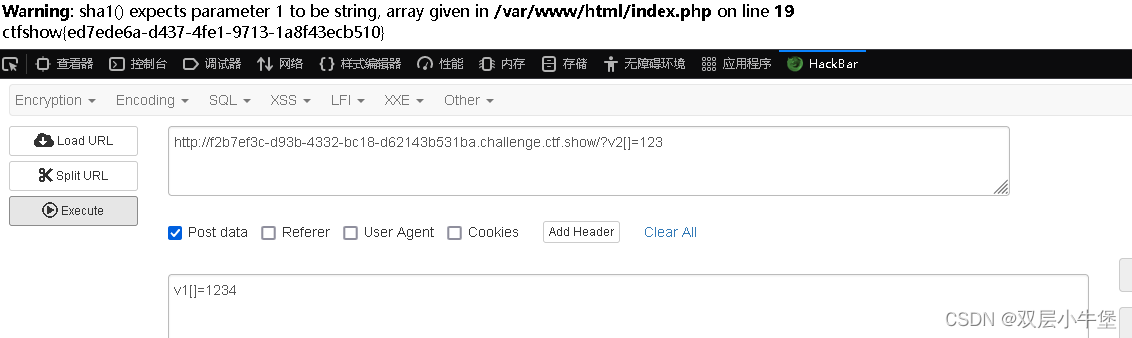
CTFSHOW php 特性
web89 数组绕过正则 include("flag.php"); highlight_file(__FILE__);if(isset($_GET[num])){$num $_GET[num]; get numif(preg_match("/[0-9]/", $num)){ 是数字 就输出 nodie("no no no!");}if(intval($num)){ 如果是存在整数 输出 flagecho …...
的排序)
2、认识O(nlogn)的排序
归并排序 分两半,谁小拷贝谁 public class Test{public static void mergeSort(int[] arr) {if (arr == null || arr.length < 2) {return;}mergeSort(arr, 0, arr.length - 1);}public static void mergeSort(int[] arr, int l, int r) {if (l == r) {return;}int mid =…...

什么是 HTTP 长轮询?
什么是 HTTP 长轮询? Web 应用程序最初是围绕客户端/服务器模型开发的,其中 Web 客户端始终是事务的发起者,向服务器请求数据。因此,没有任何机制可以让服务器在没有客户端先发出请求的情况下独立地向客户端发送或推送数据。 为…...

操作系统用户态和核心态和CPU上下文切换
目录 操作系统用户态和核心态用户态和核心态操作系统用户态和核心态是如何交换的系统调用 CPU上下文什么是CPU上下文和CPU上下文切换CPU为什么要进行上下文切换 操作系统用户态和核心态 用户态和核心态 操作系统两种状态:用户态和内核态。 操作系统的用户态和内核态…...
TSINGSEE青犀视频汇聚平台EasyCVR视频广场面包屑侧边栏支持拖拽操作
TSINGSEE青犀视频汇聚平台EasyCVR可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有GB28181、RTSP/Onvif、RTMP等,以及厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等,能对外分发RTSP、RTMP、FLV、HLS、Web…...
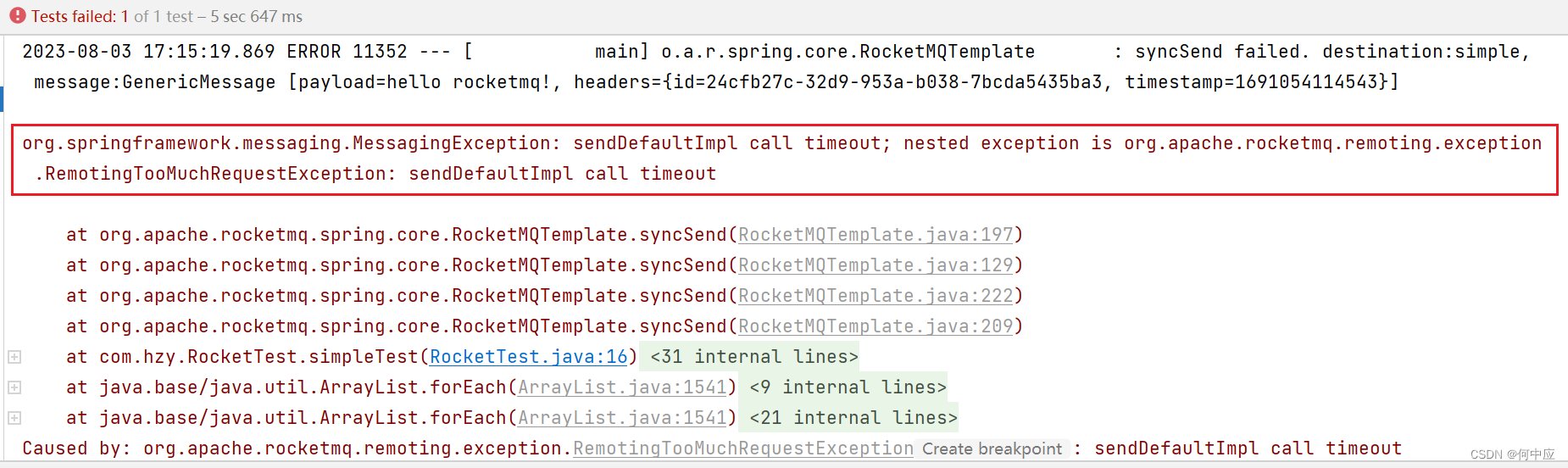
RocketMQ发送消息超时异常
说明:在使用RocketMQ发送消息时,出现下面这个异常(org.springframework.messging.MessgingException:sendDefaultImpl call timeout……); 解决:修改RocketMQ中broke.conf配置,添加下…...

WordPress做权重站:二级目录伪静态写法
我喜欢用WordPress建站,但是每个网站我都会写3个以上的二级目录,为什么了,因为WordPress数据量过大会导致数据库很大很卡,所以这种做法可以减轻数据库的负荷。我一般每个目录的文章达到15万篇就不会再更新了,3个目录加…...

浅谈下API初步认知
当我们谈论API,我们指的是应用程序接口(Application Programming Interface)。API允许不同的软件应用程序之间互相通信和交互。它定义了一组规定和协议,用于确定数据传输和请求的格式、方法和功能。 API的作用是在软件开发中提供一…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
