红黑树的历史和由来。
一个数组,1,2,3,4,5,...n; 一共n个数字。
1、直接查找
想要查询第n个数字,直接搜索,就是n次查询。
ps:那么问题来了,这样查询也太慢了,有什么改进的呢?
2、二分查找
这个时候,二分查找更快。不过就是得先把数组排好序。
乱序,二分就没有用处了。
想要查询第n个数字,二分查找,2的x次方 = n;
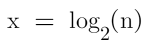
ps:问题也就出来了。每次都需要排好序。这样也太麻烦了,每次都要去做个排序,冒泡啥的,他们插入删除操作,移动元素又多,有什么比较好的解决办法吗?
3、二叉查找树(又名二叉排序树,二叉搜索树)
变成树结构
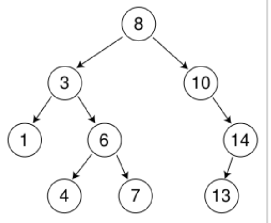
这样,查询也是和二分查找的速度差不多。
次数。其实是h 也就是高度。
h层,有2(h-1)的元素,第1层,2^(0) = 1,一共h层。那么总的数量是 N,按照二叉树排列。
S=1+2+4+8+2^(h-1) = N
按照等比数列求和的公式
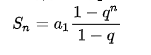

2^h-1=n
那么高度h就是相当于,
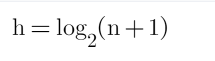
相当于二分查找。
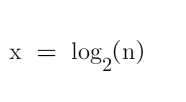
但是这个二叉树,查询快是快,但是增加,删除,修改都会带来巨大的元素移动消耗,且很难保持高效率的查询。
那么将会发生怎么样的变化?
4、AVL数(二叉平衡树) AVL,艾薇儿树。
AVL树是最早发明的自平衡二叉搜索树之一AVL 取名于两位发明者的名字G. M. Adelson-Velsky 和 E. M. Landis(来自苏联的科学家)Something interesting有人把AVL树念做“艾薇儿树”加拿大女歌手,几首不错的歌:《Complicated》、《When You're Gone》、《Innocence》
https://www.jianshu.com/p/9abaa8155ffc
每次新增,修改,删除。都会去计算每个节点的平衡因子。
也就是
| hight(左子树)-hight(右子树) | <=1
每个节点重新去算平衡。通过按住你插入的关键节点,左旋右旋的方法,调整成AVL树。
右旋,右边的旋转。往上提
左旋,左边的旋转。往上提。
LL-> R右旋。
RR->L左旋
LR - >看成 LL(RR),先RR左旋,变成LL,再右旋
RL ->看成 RR(LL),先LL右旋,变成RR,再左旋
1. 添加
可能会导致都失衡
只要让高度最低的失衡节点恢复平衡,整棵树就恢复平衡【仅需 O(1)次调整】
2. 删除
可能会导致或失衡(只有1个节点会失衡)
恢复平衡后,可能会导致更高层的祖先节点失衡【最多需要 O(logn)次调整】
3. 平均时间复杂度
搜索:O(log n)
添加:O(log n),仅需O(1)次的旋转操作
删除:O(log n),最多需要O(logn)次的旋转操作
计算机,默认底数为2.
底数一般是2 因为二分啊,快排啊,线段树啊之类的算法一般是以二分为思想的!
是的哦,AVL 因为是平衡树,所以树的高度最高是 logn 级别,各项操作也都是 logn 级别的:)
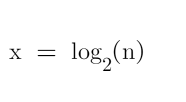
二叉平衡树。太讲究平衡了。增删改查,都是log n的级别, 如果对平衡架构没那么要求的。什么都要一般般快。
5、红黑树
相关文章:
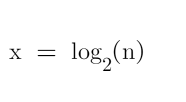
红黑树的历史和由来。
一个数组,1,2,3,4,5,...n; 一共n个数字。1、直接查找想要查询第n个数字,直接搜索,就是n次查询。ps:那么问题来了,这样查询也太慢了,有什么改进的呢?2、二分查找这个时候,二分查找更快。不过就是…...

蓝库云|制造业数字化转型为何转不动?资料处理很重要
数字化转型已经成为每个产业势在必行的课题,没有人会怀疑数字化技术与科技能解放的生产力能量,但为什么看似美好的愿景,实行起来却如此缓慢?蓝库云认为这是因为没有盖好「资料治理」的地基。 面对不断变化的法令规范要求…...

【python学习笔记】 :Lambda 函数
Lambda 函数是 Python 中的匿名函数。有些人将它们简称为lambdas,它们的语法如下: lambda arguments: expressionlambda 关键字可以用来创建一个 lambda 函数,紧跟其后的是参数列表和用冒号分割开的单个表达式。例如,lambda x: 2…...

Nginx的proxy buffer参数设置
1. proxy_buffering 语法:proxy_buffering on|off 默认值:proxy_buffering on 上下文:http,server,location作用:该指令开启从后端被代理服务器的响应body缓冲。 如果proxy_buffering开启,nginx假定被代理的后端服务器会以最…...
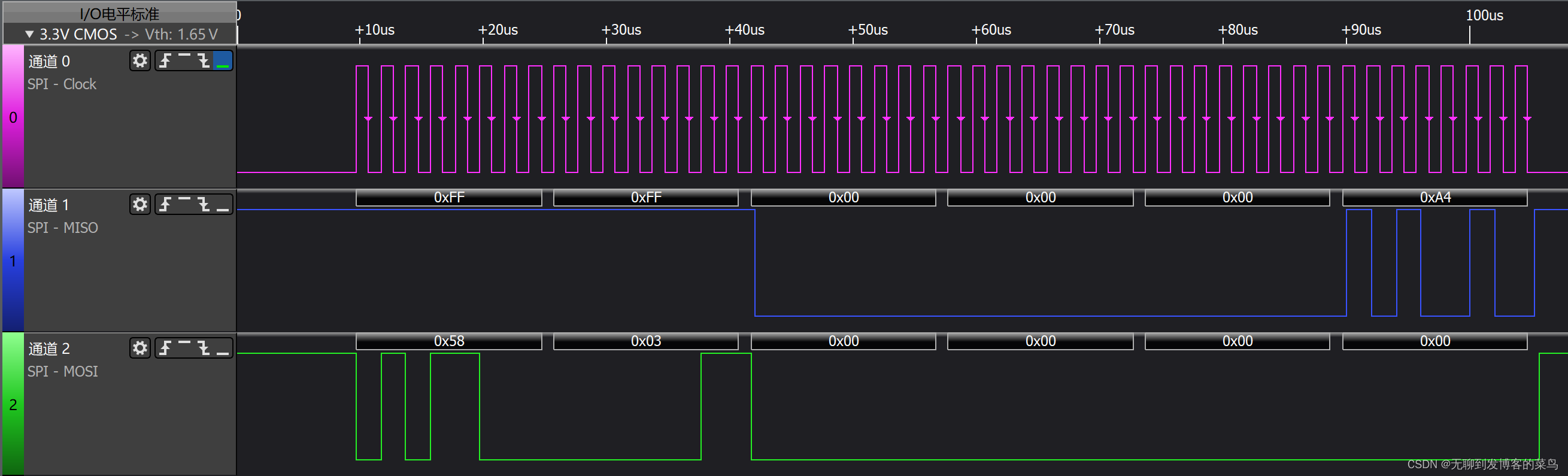
SPI简介与实例分析
SPI简介 SPI 协议是由Motorola提出的通讯协议 (Serial Peripheral Interface) ,是一种高速全双工的串行通信总线。 SPI 通讯使用 3 条总线 :SCK、 MOSI、 MISO ,以及若干片选线(SS、CS、NSS)。 主机要和哪个从机通信,就把对应的…...

通过基于pgsql的timescaleDB的time_bucket函数实现自定义聚合粒度
1、自己写的不完全满足要求的实现方式 with tb_tmp as (select *, //计算该时间距离第一天有多少天((extract(epoch from create_time) /3600/24)::integer) as ct_ifrom test.test_salary )select min(a.create_time) as create_time,sum(a.salary) from (select *,//移动数据…...
一台电脑安装26个操作系统(windows,macos,linux)
首先看看安装了哪些操作系统1-4: windows系统 四个5.Ubuntu6.deepin7.UOS家庭版8.fydeOS9.macOS10.银河麒麟11.红旗OS12.openSUSE Leap13.openAnolis14.openEuler(未安装桌面UI)15.中标麒麟(NeoKylin)16.centos17.debian Edu18.fedora19.oraclelinux20.R…...

dockerfile文件
dockerfile文件内容 Form ip端口/centos:regular ENV JAVA_HOME /E:/Program Files/Java/jdk1.8.0_351 ENV PATH $JAVA_HOME/bin:$JAVA_HOME/jre/bin:$PATH ENV LANG en_US.UTF-8 ENV LANGUAGE en_US:en ENV LC_ALL en_US.UTF-8 WORKDIR /opt COPY target/fast.jar /op…...

视觉SLAM ch11回环检测
回环检测的关键:如何有效的检测出相机经过同一个地方。如果成功的检测到可以为后端的位姿图提供更多有效数据,得到全局一致的估计。 回环检测提供了当前数据和所有历史数据的关联,还可以用回环检测进行重定位。 具体方法: 一&am…...
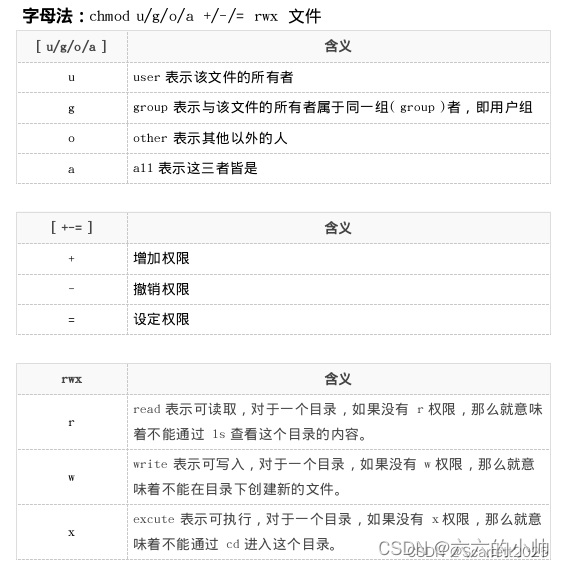
关于Ubuntu20.04文件系统思考
文章目录问题产生Ubuntu文件系统中普通用户可读写地址Ubuntu文件系统Ubuntu文件系统详解一级目录二级目录查找Ubuntu中软件安装位置Ubuntu修改文件权限问题产生 使用electron框架开发桌面端跨平台软件时,当开发完成的程序部署到Ubuntu上,系统无法产生日…...
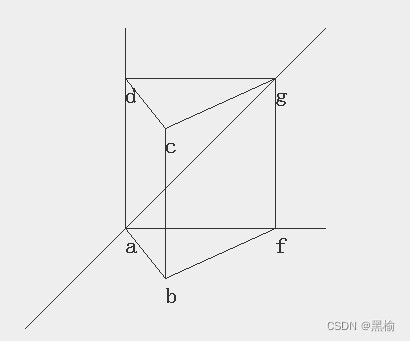
内嵌于球的等边三棱柱
( A, B )---3*30*2---( 1, 0 )( 0, 1 ) 做一个网络让输入只有3个节点,每个训练集里有两张图片,让B的训练集全为0,排列组合A,观察迭代次数平均值的变化。共完成了64组,但只有12组不同的迭代次数。 差值结构 A-B 迭代次…...
论文解读 | [CVPR2020] ContourNet:向精确的任意形状场景文本检测迈出进一步
目录 1 研究背景和目的 1.1 主要贡献: 1.2 两个挑战: 2 ContourNet 3 方法论 3.1 Adaptive-RPN 3.2 LOTM 3.3 点重定位算法 4 实验和结果 论文地址:ContourNet: Taking a Further Step toward Accurate Arbitrary-shaped Scene Tex…...

干货分享|数据可视化报表制作技巧
脑中想得再好,也要看最终的效果呈现。但偏偏有些用户分析思维不差,就是数据分析报表的制作拖了后腿,导致始终无法完美呈现数据可视化分析效果。本文将总结奥威BI软件上的常用的数据可视化报表制作技巧,供大家随时查阅。 BI数据可…...

Longhorn,企业级云原生容器分布式存储 - 备份与恢复
Longhorn,企业级云原生容器分布式存储 - 备份与恢复快照手动快照周期性快照和备份使用 Longhorn UI 设置周期性快照使用 StorageClass 设置 Recurring Jobs分离卷时允许 Recurring Job容灾卷创建容灾(DR)卷备份设置备份目标使用阿里云OSS备份存储准备工作为 S3 兼容…...

亿级高并发电商项目-- 实战篇 --万达商城项目 十(安装与配置Elasticsearch和kibana、编写搜索功能、向ES同步数据库商品数据)
亿级高并发电商项目-- 实战篇 --万达商城项目搭建 一 (商家端与用户端功能介绍、项目技术架构、数据库表结构等设计) 亿级高并发电商项目-- 实战篇 --万达商城项目搭建 一 (商家端与用户端功能介绍、项目技术架构、数据库表结构等设计&#x…...
windwos安装spring-cloud-alibaba-nacos
windwos安装spring-cloud-alibaba-nacos前言一、预备环境二、下载源码或者安装包1.启动2.关闭总结前言 这个快速开始手册是帮忙您快速在您的电脑上,下载、安装并使用 Nacos。 一、预备环境 Nacos 依赖 Java 环境来运行。如果您是从代码开始构建并运行Nacos&#x…...

Spring Boot 项目如何统一结果,统一异常,统一日志
1 统一结果返回目前的前后端开发大部分数据的传输格式都是json,因此定义一个统一规范的数据格式有利于前后端的交互与UI的展示。1.1 统一结果的一般形式是否响应成功;响应状态码;状态码描述;响应数据;其他标识符&#…...

Ubuntu下用Lean源码编译openwrt及一行命令u盘启动openwrt安装x86硬盘上
Ubuntu下用Lean源码编译openwrt 源码地址:https://github.com/coolsnowwolf/lede 1:首先微软云服务器装好 Ubuntu 64bit,推荐 Ubuntu 20.04 LTS x64,免费一年。ip设置在地球某处。总结就是每一步需要下载的都得下载完,…...

JavaScript Number 对象
JavaScript 是一门非常强大的编程语言,它提供了许多内置对象来帮助开发者在编写 JavaScript 应用时更轻松地处理数据。其中一个非常有用的对象是 JavaScript Number 对象,它可以帮助我们处理数值类型的数据,例如整数和浮点数。在本文中&#…...
【原创】java+swing+mysql银行ATM管理系统
本文主要介绍使用javaswingmysql去设计一个银行ATM管理系统,模仿实现存款、取款、转账、余额查询等功能。 功能分析: 隐含ATM管理系统一般分为管理员和用户角色,管理员可以进行用户管理、账单管理,用户可以进行转取存款等功能如…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
