11-矩阵(matrix)_方阵_对称阵_单位阵_对角阵
矩阵及其运算
[ a 11 ⋯ a 1 n ⋯ ⋯ ⋯ a m 1 ⋯ a m n ] \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \cdots & \cdots & \cdots \\ a_{m1} & \cdots & a_{mn} \\ \end{bmatrix} a11⋯am1⋯⋯⋯a1n⋯amn
矩阵就是二维数组,上面是一个 m 乘 n 的矩阵,它有 m 行,n 列,每行每列上面都有一个 元素,每个元素都有行标 i 和列标 j, 对应的元素就是
a i j a_{ij} aij
矩阵是一种常见的数据结构,它由一堆一维数组(也称为行向量)组成。矩阵是二维数组,由行和列构成。通常用于在数学、计算机科学、统计学等领域进行数据处理和表示。
矩阵可以由一堆行向量组成,这种表示方式称为行向量组成的矩阵;也可以由一堆列向量组成,称为列向量组成的矩阵。矩阵的行数表示矩阵的高度,列数表示矩阵的宽度。行向量组成的矩阵是以横向排列的行向量构成,而列向量组成的矩阵是以纵向排列的列向量构成。
例如,下面是一个由行向量组成的矩阵:
[1 2 3]
[4 5 6]
[7 8 9]
下面是一个由列向量组成的矩阵:
[1 4 7]
[2 5 8]
[3 6 9]
矩阵在线性代数、图像处理、神经网络等领域具有广泛的应用。在计算机中,矩阵也是很多数据处理算法的基础,例如矩阵乘法、矩阵转置等操作。
方阵,对称矩阵,单位矩阵,对角线
方阵
下面介绍几种特殊的矩阵,如果 m 等于 n,那就称为方阵
[ 1 0 0 0 2 0 0 0 3 ] \begin{bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{bmatrix} 100020003
对称矩阵
对称矩阵转置后不会改变原始矩阵的形状和值。
定义是 a i j a_{ij} aij
等于 a j i a_{ji} aji那么就是对称矩阵(沿着主对角线(左上角到右下角划分的线)的元素对称, 这里的对称是主对角线两侧的元素相等),并且肯定是个方阵
[ 1 1 2 1 2 3 2 3 3 ] \begin{bmatrix} 1 & 1 & 2 \\ 1 & 2 & 3 \\ 2 & 3 & 3 \\ \end{bmatrix} 112123233
单位矩阵
主对角线都是 1,其它位置是 0,这称之为单位阵,单位矩阵写为 I,一定是方阵,等同于数字里面的 1
[ 1 ⋯ 0 0 0 ⋯ 1 ⋯ 0 0 0 ⋯ ⋯ ⋯ 0 0 0 ⋯ ⋯ ⋯ 0 0 0 ⋯ 1 ] \begin{bmatrix} 1 & \cdots & 0 & 0 & 0\\ \cdots & 1 & \cdots & 0 & 0\\ 0 & \cdots & \cdots & \cdots & 0\\ 0 & 0 & \cdots & \cdots & \cdots\\ 0 & 0 & 0 & \cdots & 1\\ \end{bmatrix} 1⋯000⋯1⋯000⋯⋯⋯000⋯⋯⋯000⋯1
单位矩阵对应的方法是numpy模块中的identity和eye方法, numpy.identity返回一个单位矩阵,即一个对角线上为1,其他位置为0的方阵。
identity方法
参数:
n:一个整数,表示输出的单位矩阵的行数和列数。dtype:一个可选参数,用于指定输出数组的数据类型,默认为float类型。
返回值:
out:一个大小为n x n的NumPy数组,其主对角线为1,其余元素为0。
eye方法
numpy.eye方法用于创建一个单位矩阵,也称为单位矩阵或恒等矩阵。单位矩阵是一个方阵,它的主对角线上的元素都是1,其余元素都是0。
函数签名:
numpy.eye(N, M=None, k=0, dtype=float, order='C')
参数:
N:生成矩阵的行数(也是列数,因为是方阵)。M:可选参数,生成矩阵的列数,默认为N,因为是方阵,一般不需要指定。k:可选参数,对角线的偏移量,默认为0,表示主对角线上的元素为1,其他元素为0;若k为正整数,则主对角线在矩阵的上方,若为负整数,则主对角线在矩阵的下方,对角线元素为1。dtype:可选参数,指定生成矩阵的数据类型,默认为float。order:可选参数,指定数组的内存布局,'C'表示C顺序,'F'表示Fortran顺序,默认为'C'。
返回值:
- 返回一个单位矩阵,其形状为
(N, M)。
示例:
import numpy as np# 创建一个3x3的单位矩阵
eye_matrix = np.eye(3)
print(eye_matrix)
# 输出:
# [[1. 0. 0.]
# [0. 1. 0.]
# [0. 0. 1.]]# 创建一个4x4的单位矩阵,主对角线偏移量为1
eye_matrix_shifted = np.eye(4, k=1)
print(eye_matrix_shifted)
# 输出:
# [[0. 1. 0. 0.]
# [0. 0. 1. 0.]
# [0. 0. 0. 1.]
# [0. 0. 0. 0.]]
numpy.eye函数非常有用,特别在线性代数和矩阵运算中经常用到。
identity和eye方法的区别
numpy.eye函数与numpy.identity函数都用于创建单位矩阵,但它们有一些区别:
-
参数不同:
numpy.eye(N, M=None, k=0, dtype=float):eye函数可以创建任意大小的单位矩阵,其中N表示行数,M表示列数,默认情况下M等于N,k表示对角线的偏移量,默认为0,即主对角线。numpy.identity(n, dtype=None):identity函数创建的是一个方阵(行数等于列数),只需要一个整数n作为参数,表示输出单位矩阵的行数和列数。
-
默认值不同:
numpy.eye的默认数据类型为float,可以通过dtype参数指定其他数据类型。numpy.identity的默认数据类型也是float,可以通过dtype参数指定其他数据类型。
示例:
import numpy as np# 使用eye创建3x4的单位矩阵,对角线偏移量为1
eye_matrix = np.eye(3, 4, k=1, dtype=int)
print(eye_matrix)
# 输出:
# [[0 1 0 0]
# [0 0 1 0]
# [0 0 0 1]]# 使用identity创建3x3的单位矩阵,默认数据类型为float
identity_matrix = np.identity(3, dtype=int)
print(identity_matrix)
# 输出:
# [[1 0 0]
# [0 1 0]
# [0 0 1]]
总的来说,eye函数比identity函数更灵活,可以创建非方阵的单位矩阵,并且可以指定对角线的偏移量,而identity函数则专门用于创建方阵的单位矩阵。
对角阵
对角阵,就是主对角线非 0,其它位置是 0

dot方法在矩阵中的应用
numpy.dot方法用于计算两个数组的矩阵乘法(点积)。在矩阵运算中,矩阵乘法是一种常见的操作,它涉及到两个矩阵的元素相乘和求和的过程。
函数签名:
numpy.dot(a, b, out=None)
参数:
a:要进行矩阵乘法的数组或矩阵。b:要进行矩阵乘法的数组或矩阵。out:可选参数,指定输出结果的数组。如果不指定,结果将会创建一个新的数组。
返回值:
- 返回两个数组的矩阵乘法结果。
注意事项:
- 两个数组的维度必须满足矩阵乘法的条件,即第一个数组的列数要与第二个数组的行数相等。
- 如果两个数组是一维的,那么
dot函数将计算它们的点积(内积)。 - 如果两个数组是二维的,那么
dot函数将计算它们的矩阵乘法。
示例:
import numpy as np# 一维数组的点积(内积)
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
dot_product = np.dot(a, b)
print(dot_product) # 输出:32# 二维数组的矩阵乘法
matrix_a = np.array([[1, 2], [3, 4]])
matrix_b = np.array([[5, 6], [7, 8]])
matrix_product = np.dot(matrix_a, matrix_b)
print(matrix_product)
# 输出:
# [[19 22]
# [43 50]]
相关文章:

11-矩阵(matrix)_方阵_对称阵_单位阵_对角阵
矩阵及其运算 [ a 11 ⋯ a 1 n ⋯ ⋯ ⋯ a m 1 ⋯ a m n ] \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \cdots & \cdots & \cdots \\ a_{m1} & \cdots & a_{mn} \\ \end{bmatrix} a11⋯am1⋯⋯⋯a1n⋯amn 矩阵就是二维数组&…...
AWS多账户单点登录 IAM Identity Center(AWS SSO)
需求场景 多个aws账户,登陆麻烦且不安全,SSO单点功能并且外部身份提供者 — 如果您要管理外部身份提供者(IdP)(例如 Okta 或 Active Directory)中的用户。 官方文档:https://docs.aws.amazon.c…...
)
实验2-3-3 求奇数分之一序列前N项和 (15 分)
实验2-3-3 求奇数分之一序列前N项和 (15 分) 本题要求编写程序,计算序列 1 1/3 1/5 … 的前N项之和。 输入格式: 输入在一行中给出一个正整数N。 输出格式: 在一行中按照“sum S”的格式输出部分和的值S,精确到小数点后6位。…...

关于Android studio中的自动化测试脚本UiAutomator框架以及UiAutomatorViewer工具的使用——项目案例
加入依赖 implementation androidx.test.uiautomator:uiautomator:2.2.0创建CalcActivity页 <LinearLayout xmlns:android="http://schemas.android.com/apk/res/android"android:orientation="vertical"...

OA办公自动化系统设计与实现(论文+源码)_kaic
摘要 随着信息化建设的日益深入,无论是政府还是企事业单位,部门之间的信息沟通与协调工作越来越重要。人们迫切需要一个能充分利用网络优势,并可以管理企业的各种重要信息的软件平台,利用该平台快速建立自己的信息网络和办公管理系…...

ansible——playbook
playbook playbook是剧本的意思 通过 task 调用 ansible 的模块将多个 play 组织在一 个playbook中运行。 playbook本身由以下各部分组成: Tasks: 任务,即调用模块完成的某操作 Variables: 变量 Templates: 模板 Handlers: 处理器,当某条件…...
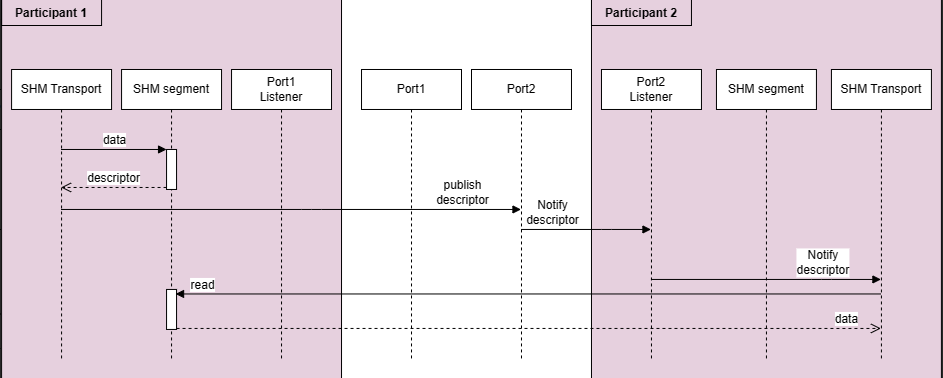
DDS中间件设计
OpenDDS、FastDDS数据分发服务中间件设计 软件架构 应用层DDS层RTPS层传输层 软件层次 FastDDS整体架构如下,这里可以看到DDS和RTPS的关系。另外缺少一部分IDL(统一描述语言),其应该是Pub、Sub的反序列化、序列化工具。 在RT…...

aws的EC2云服务器自己操作记录
亚马逊官网有免费试用1年的服务器 以下内容参考 1. 启动生成实例 1.1 创建实例时需要生成 使用的默认的 Debian 和 一个.pem后缀的秘钥 1.2 网上下一个Mobaxterm ,实例名是公有 IPv4 DNS 地址 ,使用SSH连接,登录名是admin 1.3 登录进去后 输入用户名 admin 后进去,sudo …...

基本ACL 和高级ACL配置
基本ACL 一、要求 1.全网可达 2.在1的基础上使PC1不能访问PC2 二、思路 1.通过写静态的方式使全网可达 2.配置acl主要是拒绝源IP的访问 3.在靠近目标的地方配置acl及使用 三、操作配置 1.IP及静态配置 [r1]int g0/0/0 [r1-GigabitEthernet0/0/0]ip add 123.0.0.1 24 [r…...
解决办法】)
【uniapp 报错 Cannot read properties of null (reading ‘offsetWidth‘)解决办法】
该错误通常是由于访问了一个空值的offsetWidth而引起的。解决方法如下: 检查代码中是否有访问了空值的情况,比如变量未初始化或者传入了空值参数或者事件未定义。 在操作元素之前,确保元素已经被正确加载。可以使用如下方法: <…...
6.s081/6.1810(Fall 2022)Lab2: System calls
文章目录 前言其他篇章参考链接0. 前置准备1. System call tracing (moderate)1.1 简单分析1.2 Hint 11.3 Hint 21.4 Hint 31.5 Hint 41.6 Hint 51.7 测试 2. Sysinfo (moderate)2.1 声明2.2 实现2.2.1 框架2.2.2 用户态与内核态交互2.2.3 计算空闲内存的大小2.2.4 计算非UNUSE…...

Git在VSCode中的使用
1.Git图像化界面进行项目初始化(git init) 2. Git图形化界面对文件进行操作 当我们创建一个文件时,该文件后面有一个U,表示文件未跟踪。 我们在管理工具中输入日志并提交代码,相当于做了两件事,将文件由“…...

【双指针_移动零_C++】
题目解析 移动零 nums [0,1,0,3,12] [1,3,12,0,0]算法原理 数组划分(数组分块) 双指针算法(利用数组下标来充当指针)使用两个指针的作用: cur指针:从左往右扫描数组,就是遍历数组。 dest指针…...

【网络安全】网络安全威胁实时地图 - 2023
文章目录 [TOC] ① 360 安全大脑360 APT全景雷达 ② 瑞星杀毒瑞星云安全瑞星网络威胁态势感知平台 ③ 比特梵德 Bitdefender④ 飞塔防火墙 FortiGuard⑤ 音墙网络 Sonicwall⑥ 捷邦 Check Point⑦ AO卡巴斯基实验室全球模拟隧道模拟 ⑧ 数字攻击地图⑨ Threatbutt互联网黑客攻击…...
视频过大如何压缩变小?文件压缩技巧分享
如何压缩视频是许多视频编辑者、视频上传者经常遇到的问题,如果你也遇到了这个问题,不用担心,下面将就给大家分享几个视频压缩方法,可以帮助大家轻松地压缩视频,同时保持视频的高清晰度和音频质量。 一、嗨格式压缩大师…...
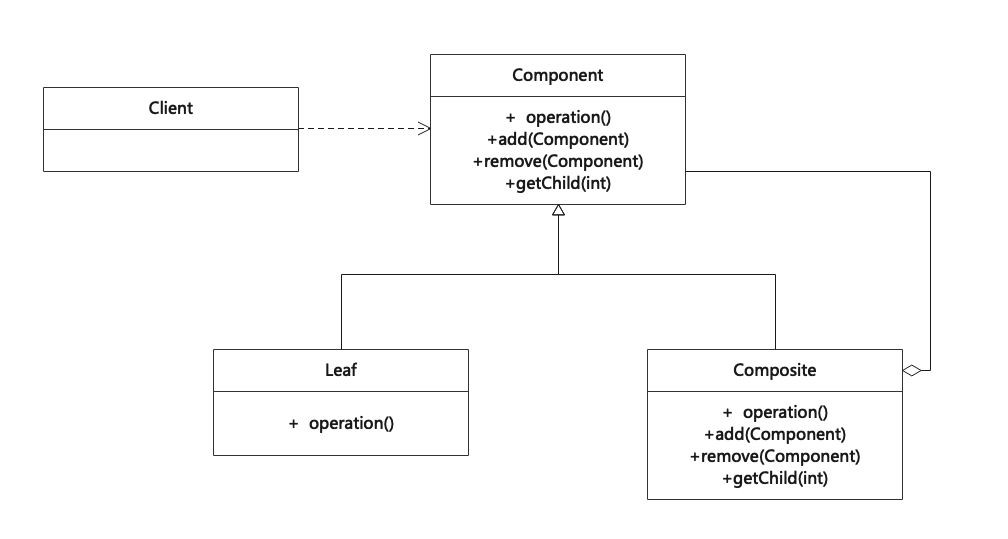
组合模式(Composite)
组合模式是一种结构型设计模式,主要用来将多个对象组织成树形结构以表示“部分-整体”的层次结构,因此该模式也称为“部分-整体”模式。简言之,组合模式就是用来将一组对象组合成树状结构,并且能像使用独立对象一样使用它们。 Co…...
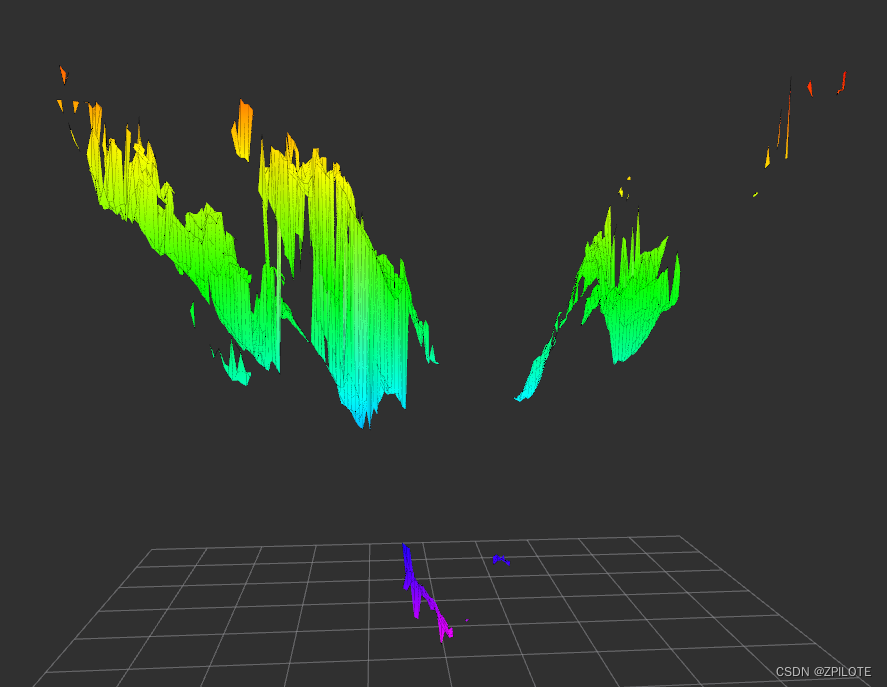
grid map学习笔记3之详解grid_map_pcl库实现point cloud点云转换成grid map栅格地图
文章目录 0 引言1 grid_map_pcl示例1.1 主要文件1.2 示例数据1.3 启动文件1.4 配置文件1.5 主要实现流程1.6 启动示例1.7 示例结果 2 D435i 点云生成栅格地图2.1 D435i 点云文件2.2 修改启动文件2.3 测试和结果2.4 修改配置文件2.5 重新测试和结果 0 引言 grid map学习笔记1已…...

ebpf开发问题汇总
不同Programs之间通信 用bpf_obj_get来获取MAP的描述符,然后用bpf_map_reuse_fd函数来在不同program之间复用 kernel 与 user space之间 需要pin the BPF MAP to the BPF Virtual File System (VFS),来持久化存储,否则如果map用不到会被destory 引用…...

认识 mysql 命令
文章目录 1.简介2.选项3.子命令4.小结参考文献 1.简介 mysql 是 MySQL 的命令行客户端工具,用于连接到 MySQL 服务器并执行 SQL 语句。 它支持交互式和非交互式两种使用方式。以交互方式使用时,查询结果以 ASCII 表格式呈现。 当以非交互方式使用时&am…...
)
IK(Inverse Kinematics,逆运动学)
介绍 在Unity中,IK(Inverse Kinematics,逆运动学)是一种用于控制角色或物体骨骼的技术。通过使用IK,可以实现更自然和真实的动画效果,特别是在处理复杂的角色动作时非常有用。 IK Pass是Unity中的一个功能…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
