LeetCode404. 左叶子之和
404. 左叶子之和
文章目录
- [404. 左叶子之和](https://leetcode.cn/problems/sum-of-left-leaves/)
- 一、题目
- 二、题解
- 方法一:递归
- 方法二:迭代
一、题目
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:

输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1]
输出: 0
提示:
- 节点数在
[1, 1000]范围内 -1000 <= Node.val <= 1000
二、题解
方法一:递归
算法思路:
题目要求计算二叉树中所有左叶子节点的值之和。我们可以使用递归来解决这个问题。递归的思想是,对于每个节点,我们判断它是否是左叶子节点,如果是,则将其值加到结果中,然后递归地处理它的左子树和右子树。
具体实现:
-
我们首先定义一个变量
sum来保存左叶子节点值的和,并初始化为0。 -
在递归函数
sumOfLeftLeaves中,我们首先检查当前节点是否为空,如果为空,则返回0。 -
然后,我们检查当前节点的左子节点是否存在,以及左子节点是否为叶子节点。如果是叶子节点,则将其值加到
sum中。 -
最后,我们递归地处理当前节点的左子树和右子树,将它们的返回值累加到
sum中。 -
在每一层递归结束后,函数返回当前子树中左叶子节点的值之和。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {int sum = 0;if (root == nullptr) {return 0;}// 判断左子节点是否为叶子节点,如果是则将值加入 sumif (root->left && !root->left->left && !root->left->right) {sum += root->left->val;}// 递归处理左子树和右子树,并累加结果到 sumreturn sum + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);}
};
算法分析:
-
时间复杂度:遍历整个二叉树的时间复杂度为 O(N),其中 N 是二叉树的节点数。在每个节点上,我们进行常数时间的判断和加法操作。
-
空间复杂度:递归函数的调用会占用栈空间,递归的深度最坏情况下为树的高度,所以空间复杂度为 O(H),其中 H 是二叉树的高度。在最坏情况下,二叉树可能退化为链表,高度为 N,此时空间复杂度为 O(N)。但在一般情况下,二叉树的高度平衡,空间复杂度会接近 O(logN)。
方法二:迭代
算法思路:
- 我们可以使用深度优先搜索(DFS)来遍历二叉树,使用栈来辅助遍历。
- 在遍历的过程中,对于每个节点,我们检查它的左子节点是否存在,如果存在,继续检查左子节点是否为叶子节点(即没有左右子节点)。如果是叶子节点,则将其值加到累加器
sum中。 - 对于非叶子节点,我们将左子节点压入栈,以便后续继续检查。
- 然后,无论是否有右子节点,都将右子节点压入栈,以确保我们遍历了所有可能的路径。
具体实现:
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {stack<TreeNode*> st;int sum = 0;if (root == nullptr) {return 0;}st.push(root);while (!st.empty()) {TreeNode* node = st.top();st.pop();if (node->left) {if (!node->left->left && !node->left->right) {sum += node->left->val; // 如果左子节点是叶子节点,将值加入 sum} else {st.push(node->left); // 如果左子节点不是叶子节点,将左子节点压入栈}}if (node->right) {st.push(node->right); // 将右子节点压入栈,无论是否为叶子节点}}return sum;}
};
算法分析:
- 时间复杂度:遍历整个二叉树的时间复杂度为 O(N),其中 N 是二叉树的节点数。在每个节点上,我们进行常数时间的判断、加法和栈操作。
- 空间复杂度:使用了一个栈来辅助遍历,栈的空间占用与二叉树的高度相关,最坏情况下为 O(N)。因此,总体空间复杂度为 O(N)。
相关文章:

LeetCode404. 左叶子之和
404. 左叶子之和 文章目录 [404. 左叶子之和](https://leetcode.cn/problems/sum-of-left-leaves/)一、题目二、题解方法一:递归方法二:迭代 一、题目 给定二叉树的根节点 root ,返回所有左叶子之和。 示例 1: 输入: root [3,9…...
Nginx 高性能内存池 ----【学习笔记】
跟着这篇文章学习: c代码实现一个高性能内存池(超详细版本)_c 内存池库_linux大本营的博客-CSDN博客https://blog.csdn.net/qq_40989769/article/details/130874660以及这个视频学习: nginx的内存池_哔哩哔哩_bilibilihttps://w…...
iOS--frame和bounds
坐标系 首先,我们来看一下iOS特有的坐标系,在iOS坐标系中以左上角为坐标原点,往右为X正方向,往下是Y正方向如下图: bounds和frame都是属于CGRect类型的结构体,系统的定义如下,包含一个CGPoint…...
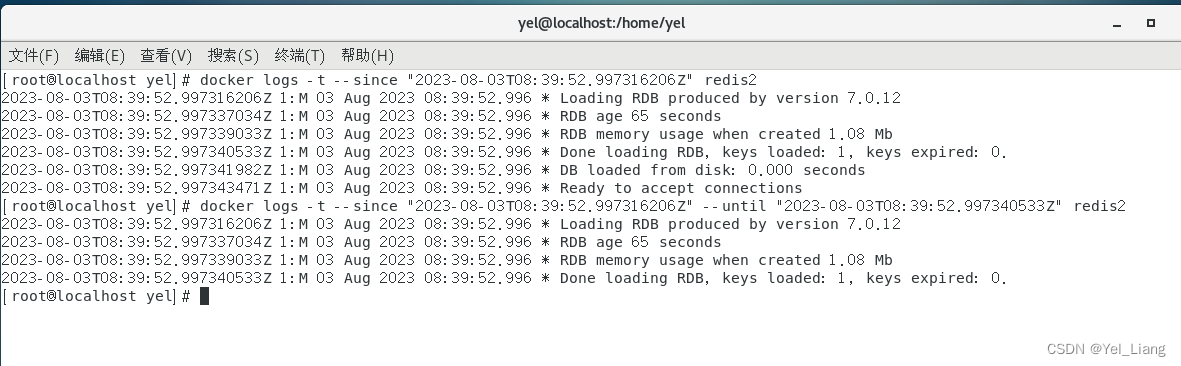
docker logs 使用说明
docker logs 可以查看某个容器内的日志情况。 前置参数说明 c_name容器名称 / 容器ID logs 获取容器的日志 , 命令如下: docker logs [options] c_name option参数: -n 查看最近多少条记录:docker logs -n 5 c_name--tail与-n 一样 &#…...
)
Ceph入门到精通-Ceph PG状态详细介绍(全)
本文主要介绍PG的各个状态,以及ceph故障过程中PG状态的转变。 Placement Group States(PG状态) creating Ceph is still creating the placement group. Ceph 仍在创建PG。activating The placement group is peered but not yet active.…...
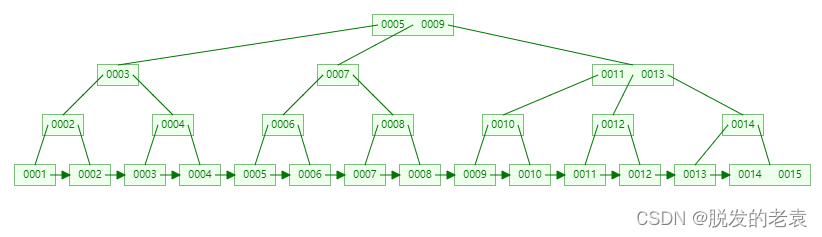
【数据结构】二叉树、二叉搜索树、平衡二叉树、红黑树、B树、B+树
概述 二叉树(Binary Tree):每个节点最多有两个子节点(左子节点和右子节点),没有限制节点的顺序。特点是简单直观,易于实现,但查找效率较低。 二叉搜索树(Binary Search…...

【JVM】(二)深入理解Java类加载机制与双亲委派模型
文章目录 前言一、类加载过程1.1 加载(Loading)1.2 验证(Verification)1.3 准备(Preparation)1.4 解析(Resolution)1.5 初始化(Initialization) 二、双亲委派…...
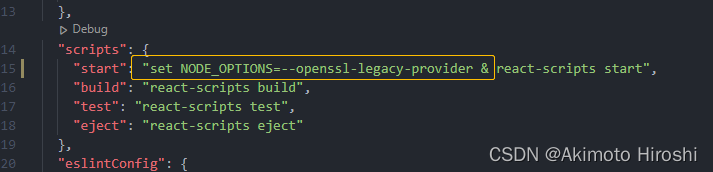
npm i 报错项目启动不了解决方法
1.场景 在另一台电脑低版本node环境跑的react项目,换到另一台电脑node18环境执行npm i时候报错 2.解决方法 脚本前加上set NODE_OPTIONS--openssl-legacy-provider...

【从零开始学习JAVA | 第三十七篇】初识多线程
目录 前言: 编辑 引入: 多线程: 什么是多线程: 多线程的意义: 多线程的应用场景: 总结: 前言: 本章节我们将开始学习多线程,多线程是一个很重要的知识点ÿ…...
微信新功能,你都知道吗?
近日iOS 微信8.0.40正式版来了,一起来看看有哪些变化? 1、朋友圈置顶 几个月前微信开始内测「朋友圈置顶」功能,从网友们的反馈来看,iOS 微信 8.0.40 似乎扩大了内测范围,更多用户可以体验到该功能了。 大家可以去自己…...
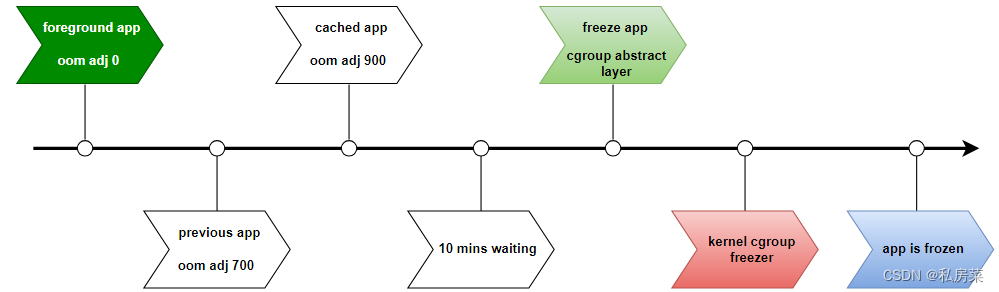
Android 中 app freezer 原理详解(二):S 版本
基于版本:Android S 0. 前言 在之前的两篇博文《Android 中app内存回收优化(一)》和 《Android 中app内存回收优化(二)》中详细剖析了 Android 中 app 内存优化的流程。这个机制的管理通过 CachedAppOptimizer 类管理,为什么叫这个名字,而不…...

Vue3_04_ref 函数和 reactive 函数
ref 函数 声明变量时,赋值的值要写在 ref() 函数中修改变量时,变量名.value xxx在模板中使用时可以省略掉 .value,直接使用变量名即可 <template><h1>一个人的信息</h1><h2>姓名:{{name}}</h2><…...
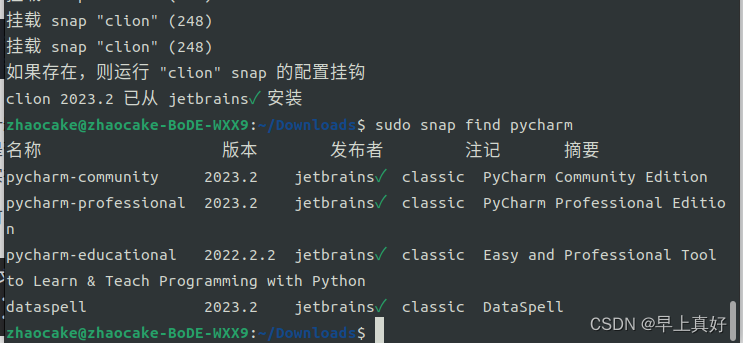
05 Ubuntu下安装.deb安装包方式安装vscode,snap安装Jetbrains产品等常用软件
使用deb包安装类型 deb包指的其实就是debian系统,ubuntu系统是基于debian系统的发行版。 一般我们会到需要的软件官网下载deb安装包,然后你既可以采用使用“软件安装”打开的方法来进行安装,也可以使用命令行进行安装。我推荐后者ÿ…...

性能测试jmeter连接数据库jdbc(sql server举例)
一、下载第三方工具包驱动数据库 1. 因为JMeter本身没有提供链接数据库的功能,所以我们需要借助第三方的工具包来实现。 (有这个jar包之后,jmeter可以发起jdbc请求,没有这个jar包,也有jdbc取样器,但不能发起…...
8.3 C高级 Shell脚本
写一个脚本,包含以下内容: 显示/etc/group文件中第五行的内容创建目录/home/ubuntu/copy切换工作路径到此目录赋值/etc/shadow到此目录,并重命名为test将当前目录中test的所属用户改为root将test中其他用户的权限改为没有任何权限 #!/bin/b…...

2023年华数杯A题
A 题 隔热材料的结构优化控制研究 新型隔热材料 A 具有优良的隔热特性,在航天、军工、石化、建筑、交通等 高科技领域中有着广泛的应用。 目前,由单根隔热材料 A 纤维编织成的织物,其热导率可以直接测出;但是 单根隔热材料 A 纤维…...

【零基础学Rust | 基础系列 | 函数,语句和表达式】函数的定义,使用和特性
文章标题 简介一,函数1,函数的定义2,函数的调用3,函数的参数4,函数的返回值 二,语句和表达式1,语句2,表达式 总结: 简介 在Rust编程中,函数,语句…...

加解密算法+压缩工具
sha256 工具类 package com.fanghui.vota.packages.util;import org.slf4j.Logger; import org.slf4j.LoggerFactory;import java.io.File; import java.io.FileInputStream; import java.io.FileNotFoundException; import java.io.IOException; import java.math.BigInteger…...

FeignClient接口的几种方式总结
FeignClient这个注解,已经封装了远程调用协议。在springboot的开发,或者微服务的开发过程中,我们需要跨服务调用,或者调用外部的接口,我们都可以使用FeignClient。 一、FeignClient介绍 FeignClient 注解是 Spring Cl…...
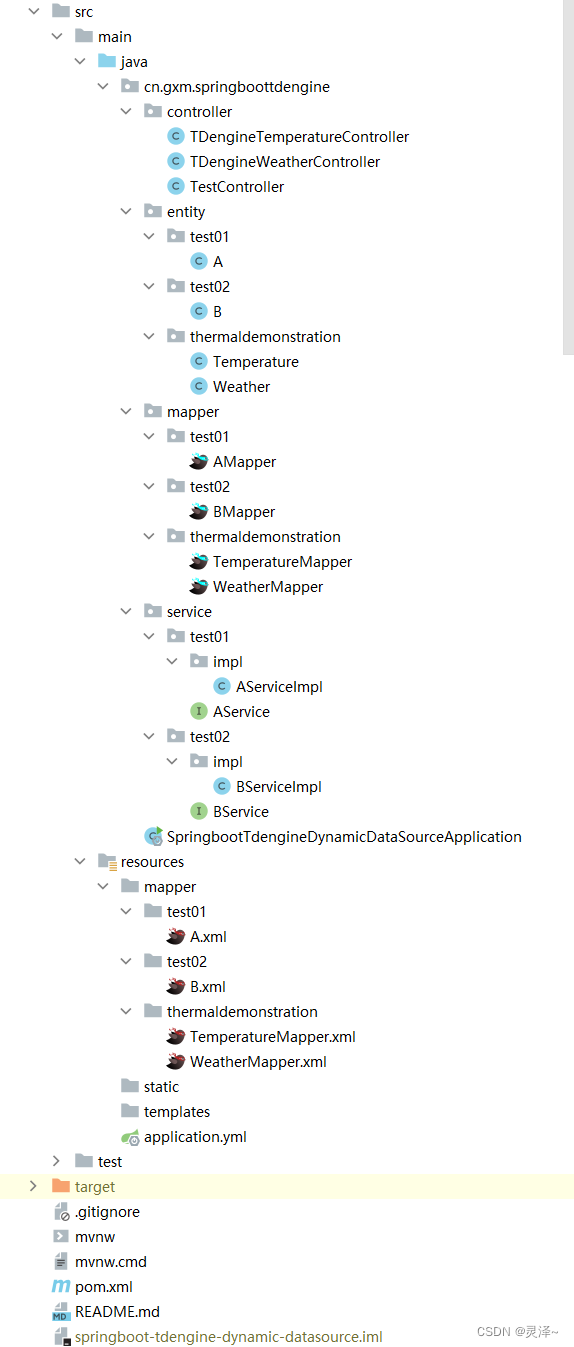
springBoot多数据源使用tdengine(3.0.7.1)+MySQL+mybatisPlus+druid连接池
一、安装部署 1、我这里使用的 3.0.7.1版本,因为我看3.x版本已经发布了一年了,增加了很多新的功能,而且3.x官方推荐,对于2.x的版本,官网都已经推荐进行升级到3.x,所以考虑到项目以后的发展,决定…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
