2023年第四届“华数杯”数学建模思路 - 案例:异常检测
文章目录
- 赛题思路
- 一、简介 -- 关于异常检测
- 异常检测
- 监督学习
- 二、异常检测算法
- 2. 箱线图分析
- 3. 基于距离/密度
- 4. 基于划分思想
赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
一、简介 – 关于异常检测
异常检测(outlier detection)在以下场景:
- 数据预处理
- 病毒木马检测
- 工业制造产品检测
- 网络流量检测
等等,有着重要的作用。由于在以上场景中,异常的数据量都是很少的一部分,因此诸如:SVM、逻辑回归等分类算法,都不适用,因为:
监督学习算法适用于有大量的正向样本,也有大量的负向样本,有足够的样本让算法去学习其特征,且未来新出现的样本与训练样本分布一致。
以下是异常检测和监督学习相关算法的适用范围:
异常检测
- 信用卡诈骗
- 制造业产品异常检
- 数据中心机器异常检
- 入侵检测
监督学习
- 垃圾邮件识别
- 新闻分类
二、异常检测算法

import tushare
from matplotlib import pyplot as pltdf = tushare.get_hist_data("600680")
v = df[-90: ].volume
v.plot("kde")
plt.show()
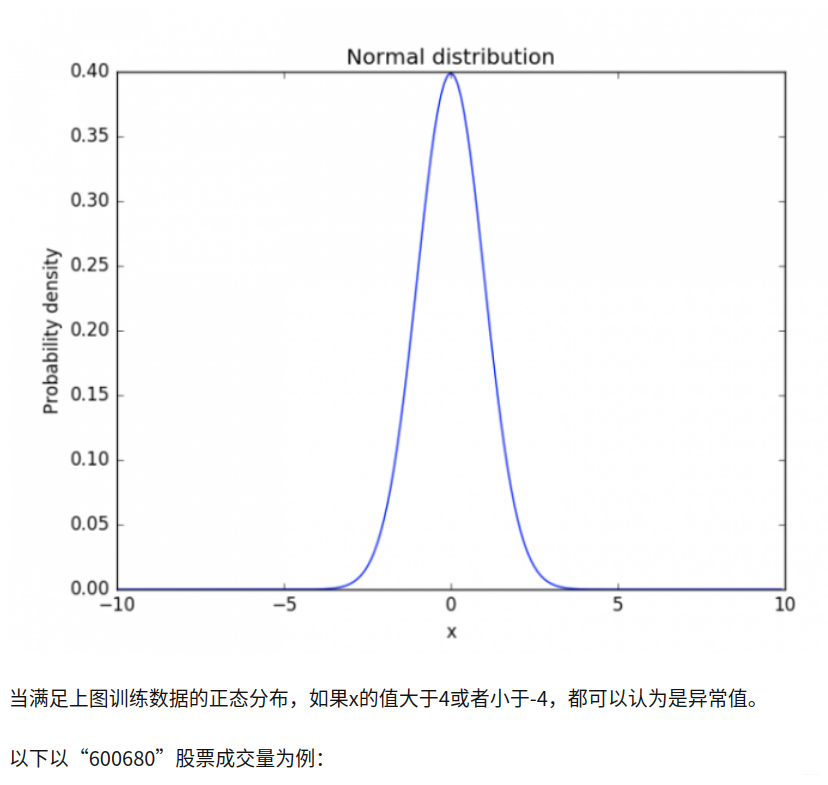
近三个月,成交量大于200000就可以认为发生了异常(天量,嗯,要注意风险了……)
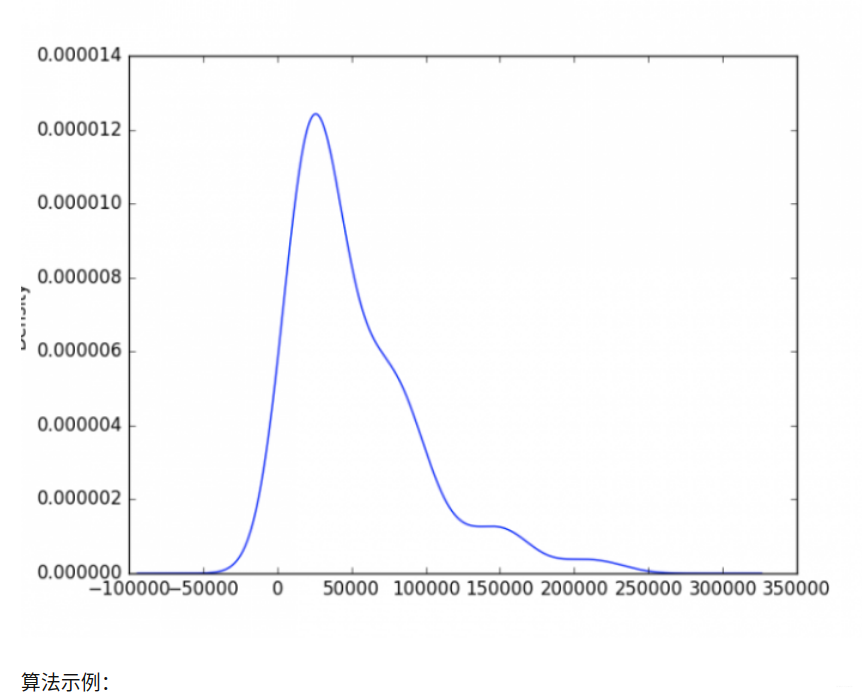

2. 箱线图分析
import tushare
from matplotlib import pyplot as pltdf = tushare.get_hist_data("600680")
v = df[-90: ].volume
v.plot("kde")
plt.show()
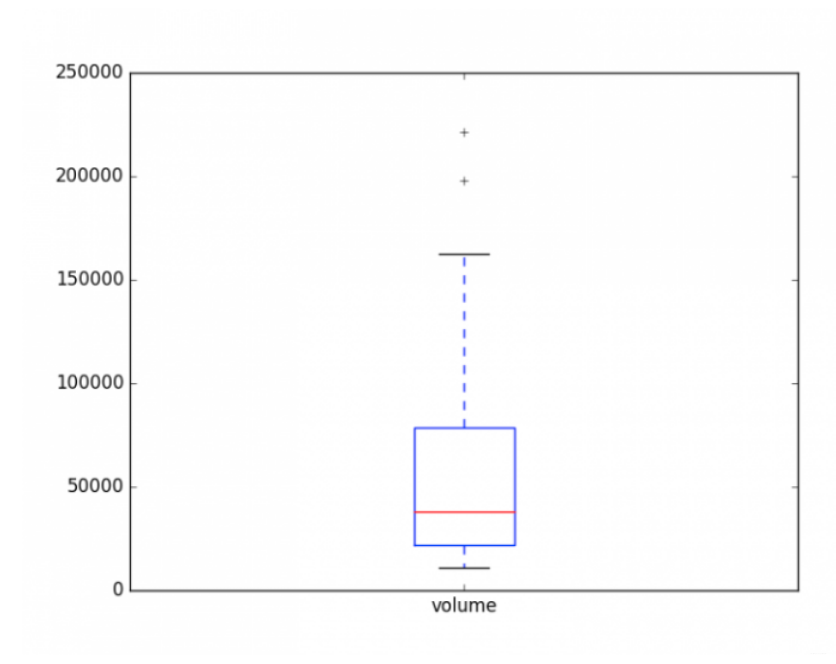
大体可以知道,该股票在成交量少于20000,或者成交量大于80000,就应该提高警惕啦!
3. 基于距离/密度
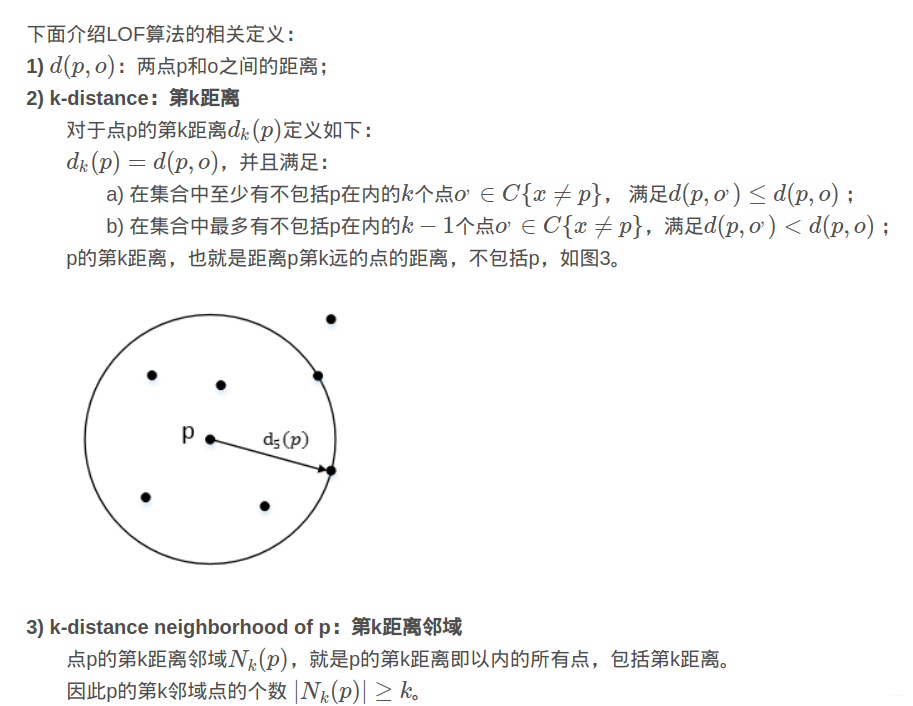
典型的算法是:“局部异常因子算法-Local Outlier Factor”,该算法通过引入“k-distance,第k距离”、“k-distance neighborhood,第k距离邻域”、“reach-distance,可达距离”、以及“local reachability density,局部可达密度 ”和“local outlier factor,局部离群因子”,来发现异常点。
用视觉直观的感受一下,如图2,对于C1集合的点,整体间距,密度,分散情况较为均匀一致,可以认为是同一簇;对于C2集合的点,同样可认为是一簇。o1、o2点相对孤立,可以认为是异常点或离散点。现在的问题是,如何实现算法的通用性,可以满足C1和C2这种密度分散情况迥异的集合的异常点识别。LOF可以实现我们的目标。

4. 基于划分思想
典型的算法是 “孤立森林,Isolation Forest”,其思想是:
假设我们用一个随机超平面来切割(split)数据空间(data space), 切一次可以生成两个子空间(想象拿刀切蛋糕一分为二)。之后我们再继续用一个随机超平面来切割每个子空间,循环下去,直到每子空间里面只有一个数据点为止。直观上来讲,我们可以发现那些密度很高的簇是可以被切很多次才会停止切割,但是那些密度很低的点很容易很早的就停到一个子空间了。
这个的算法流程即是使用超平面分割子空间,然后建立类似的二叉树的过程:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForestrng = np.random.RandomState(42)# Generate train data
X = 0.3 * rng.randn(100, 2)
X_train = np.r_[X + 1, X - 3, X - 5, X + 6]
# Generate some regular novel observations
X = 0.3 * rng.randn(20, 2)
X_test = np.r_[X + 1, X - 3, X - 5, X + 6]
# Generate some abnormal novel observations
X_outliers = rng.uniform(low=-8, high=8, size=(20, 2))# fit the model
clf = IsolationForest(max_samples=100*2, random_state=rng)
clf.fit(X_train)
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)# plot the line, the samples, and the nearest vectors to the plane
xx, yy = np.meshgrid(np.linspace(-8, 8, 50), np.linspace(-8, 8, 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)plt.title("IsolationForest")
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='green')
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='red')
plt.axis('tight')
plt.xlim((-8, 8))
plt.ylim((-8, 8))
plt.legend([b1, b2, c],["training observations","new regular observations", "new abnormal observations"],loc="upper left")
plt.show()

相关文章:

2023年第四届“华数杯”数学建模思路 - 案例:异常检测
文章目录 赛题思路一、简介 -- 关于异常检测异常检测监督学习 二、异常检测算法2. 箱线图分析3. 基于距离/密度4. 基于划分思想 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 一、简介 – 关于异常检测 异常…...

inline的盒子设置transform不生效
目录 如何遇到的问题原因为什么会这样怎么解决 如何遇到的问题 最近在开发过程中,因为需要对一个icon进行旋转,而icon本身,是设置span的伪类来进行的,结果我发现无论怎么设置transform都无法使其生效。 span::before {font-famil…...
————词典分词)
自然语言处理学习笔记(四)————词典分词
目录 1.中文分词 2.词典分词 (1)词的定义 (2)词典性质——齐夫定律 (3)词典 (4)加载词典 (5)hanlp词典路径 1.中文分词 中文分词:指的是将一…...

jsoncpp库和nlohmann-json库实现JSON与字符串类型转换
在ROS中,可以使用jsoncpp库来实现JSON与字符串类型之间的转换。jsoncpp是ROS自带的一个JSON库,它提供了一些函数来解析和生成JSON数据。 下面是一个使用jsoncpp库实现JSON与字符串类型转换的示例代码: #include <ros/ros.h> #include…...

20230803 函数传参引用
定义多输出变量的函数时,通过直接传参数内存地址在函数内部直接修改外部变量的值。需要定义函数时 在输入参数前加 引用符号 & 。 C 值传递、指针传递、引用传递详解...
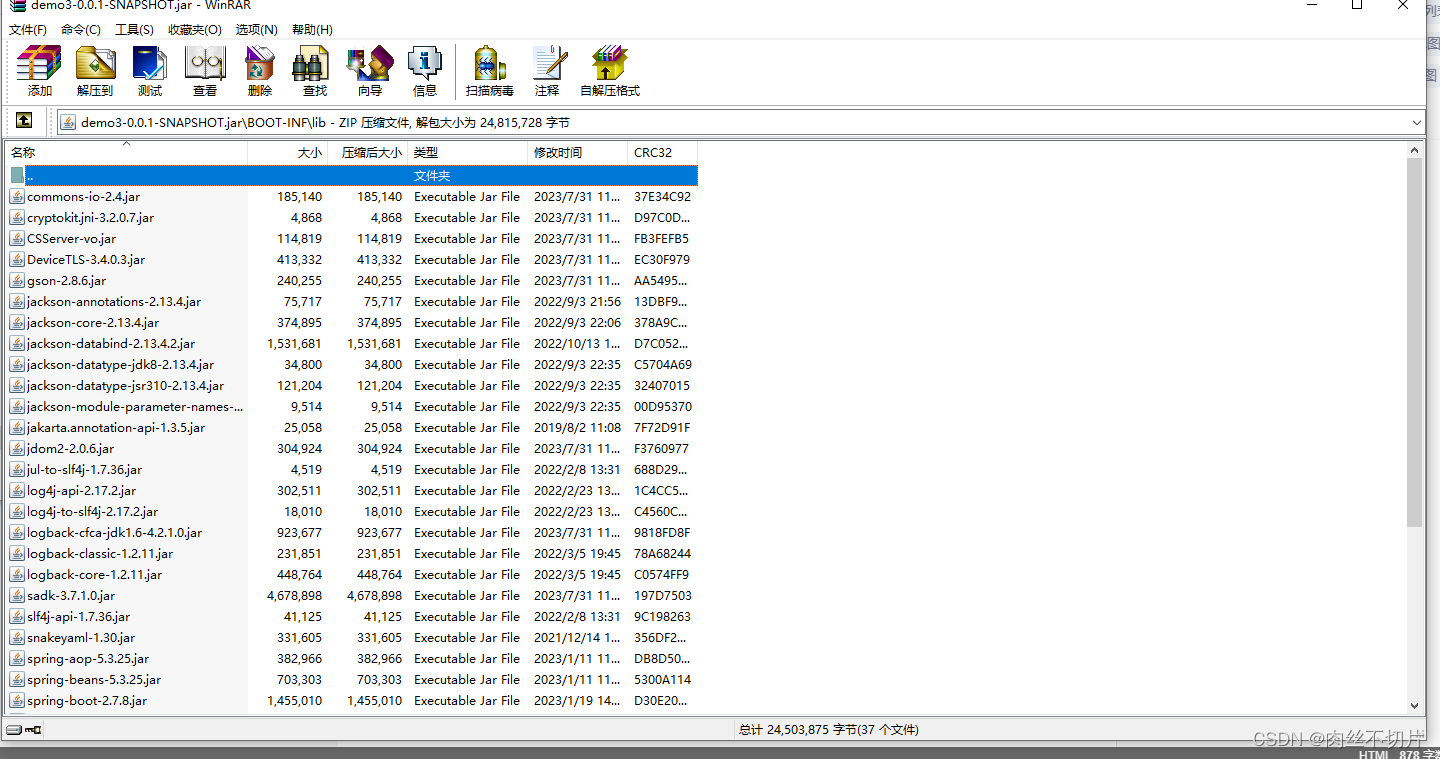
IDEA SpringBoot项目引入外部jar并打包
1、首先,我们再pom.xml中导入依赖包时,打包可以正常进行。 但如果我们引入了第三方的外部jar包(这里需要先把jar包添加到该项目依赖库中,这里不做演示),如图 2、导致打包时报错,程序包不存在或…...

ModaHub魔搭社区——阿里云通义千问宣布开源!70亿参数模型上线魔搭社区,免费可商用
通义千问开源!8月3日,AI模型社区魔搭ModaHub上架两款开源模型Qwen-7B和Qwen-7B-Chat,阿里云确认其为通义千问70亿参数通用模型和对话模型,两款模型均开源、免费、可商用。在多个权威测评中,通义千问7B模型取得了远超国内外同等尺寸模型的效果,成为当下业界最强的中英文7B…...

Jenkins 自动化部署实例讲解,另附安装教程!
【2023】Jenkins入门与安装_jenkins最新版本_丶重明的博客-CSDN博客 也可以结合这个互补看 前言 你平常在做自己的项目时,是否有过部署项目太麻烦的想法?如果你是单体项目,可能没什么感触,但如果你是微服务项目,相…...
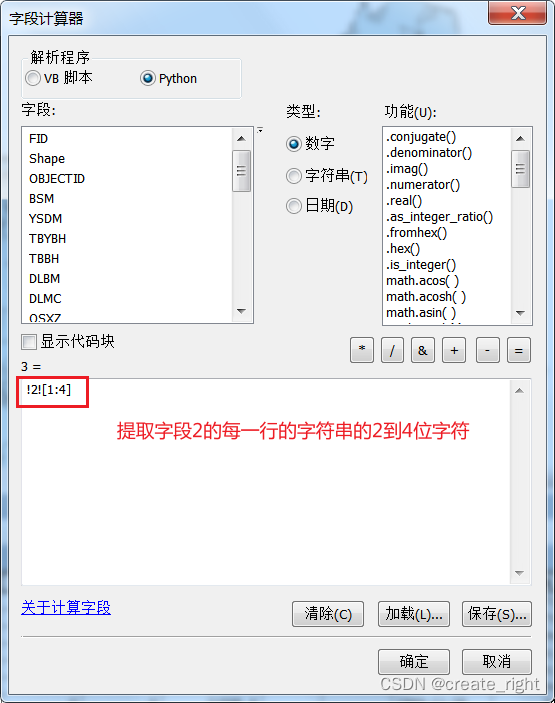
arcgis字段计算器
1、两字段叠加。要求待叠加的字段类型为文本或字符串类型。如下: 2、字符串部分提取。...
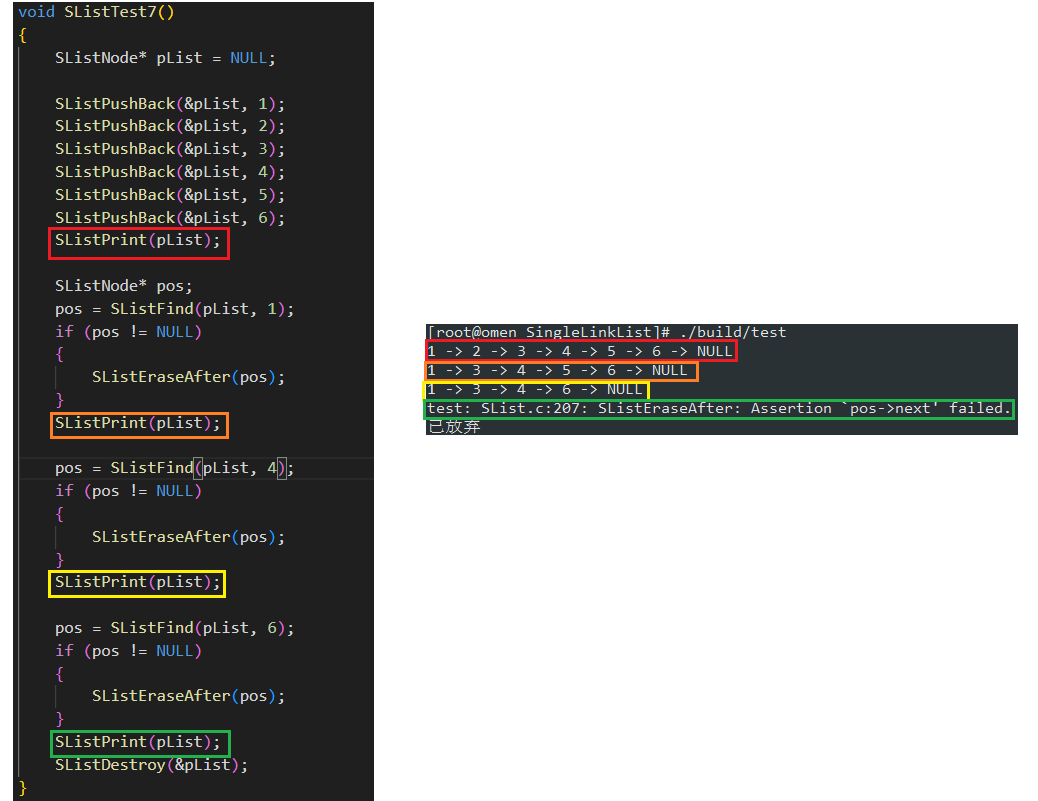
数据结构: 线性表(无哨兵位单链表实现)
文章目录 1. 线性表的链式表示: 链表1.1 顺序表的优缺点1.2 链表的概念1.3 链表的优缺点1.4 链表的结构 2. 单链表的定义2.1 单链表的结构体2.2 接口函数 3. 接口函数的实现3.1 动态申请一个结点 (BuySListNode)3.2 单链表打印 (SListPrint)3.3 单链表尾插 (SListPushBack)3.4 …...

Exploring the Underlying Architecture of CSS3
引言 在现代的网页设计中,CSS(层叠样式表)起着至关重要的作用。CSS3作为最新的CSS标准,引入了许多令人兴奋的功能和特性。但是,要真正理解CSS3的底层架构实现原理,对于前端开发者来说,是非常重…...

方差分析||判断数据是否符合正态分布
方差分析练习题 练习学习笔记: (1) 标准差和标准偏差、均方差是一个东西。标准误差和标准误是一个东西。这两个东西有区别。 (2)单因素方差分析(MATLAB求解) (3)使用an…...

java linq多字段排序时间比较
public static void main(String[] args) {//100万条数据List<CrmInvestSaleUserCount> waitAssignUserList new ArrayList<>();for (int i 0; i < 1000000; i) {waitAssignUserList.add(new CrmInvestSaleUserCount().setSales_username("test" i…...

【c++】rand()随机函数的应用(二)——舒尔特方格数字的生成
目录 一、舒尔特方格简介 二、如何生成舒尔特方格 (一)线性同余法 1、利用线性同余法生成随机数序列的规律 (1) 当a和c选取合适的数时,可以生成周期为m的随机数序列 (2) 种子seed取值也是有周期的 2、利用线性同余法生成5阶舒尔特方格…...

“深入剖析JVM内部机制:探索Java虚拟机的运行原理“
标题:深入剖析JVM内部机制:探索Java虚拟机的运行原理 摘要:本文将深入探讨Java虚拟机(JVM)的内部机制,包括类加载、内存管理、垃圾回收、即时编译等关键概念和原理,帮助开发者更好地理解JVM的运…...

pandas 新增数据列的几种方式
准备数据 将下面的数据存到csv中 ymd,bWendu,yWendu,tianqi,fengxiang,fengli,aqi,aqiInfo,aqiLevel 2018-01-01,3℃,-6℃,晴~多云,东北风,1-2级,59,良,2 2018-01-02,2℃,-5℃,阴~多云,东北风,1-2级,49,优,1 2018-01-03,2℃,-5℃,多云,北风,1-2级,28,优,1 2018-01-04,0℃,-8℃…...
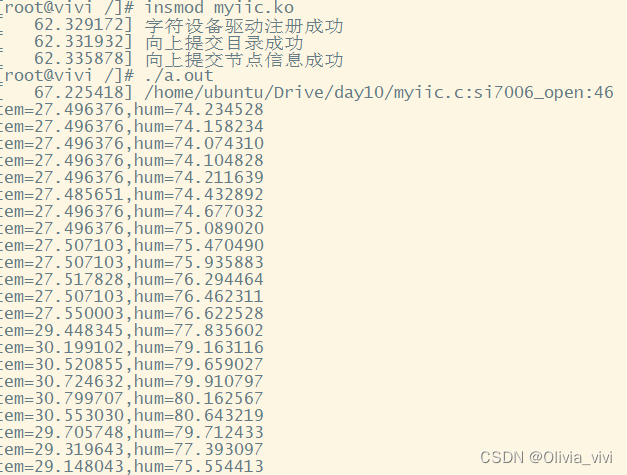
linux_驱动_iic总线获取si7006温湿度
应用层si7006.c #include<stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <unistd.h> #include <stdlib.h> #include <string.h> #include <sys/ioctl.h> #include <arpa/inet.h>…...
虚拟机网络图标不见了
有3台虚拟机之前正常运行的,有一天打开虚拟机发现2台虚拟机的网络连接图标不见了,也ping不通另外两台。 解决:在终端执行以下命令,即可ping通 [roothadoop103 ~]# sudo nmcli network off [roothadoop103 ~]# sudo nmcli network…...
CTF:信息泄露.(CTFHub靶场环境)
CTF:信息泄露.(CTFHub靶场环境) “ 信息泄露 ” 是指网站无意间向用户泄露敏感信息,泄露了有关于其他用户的数据,例如:另一个用户名的财务信息,敏感的商业 或 商业数据 ,还有一些有…...
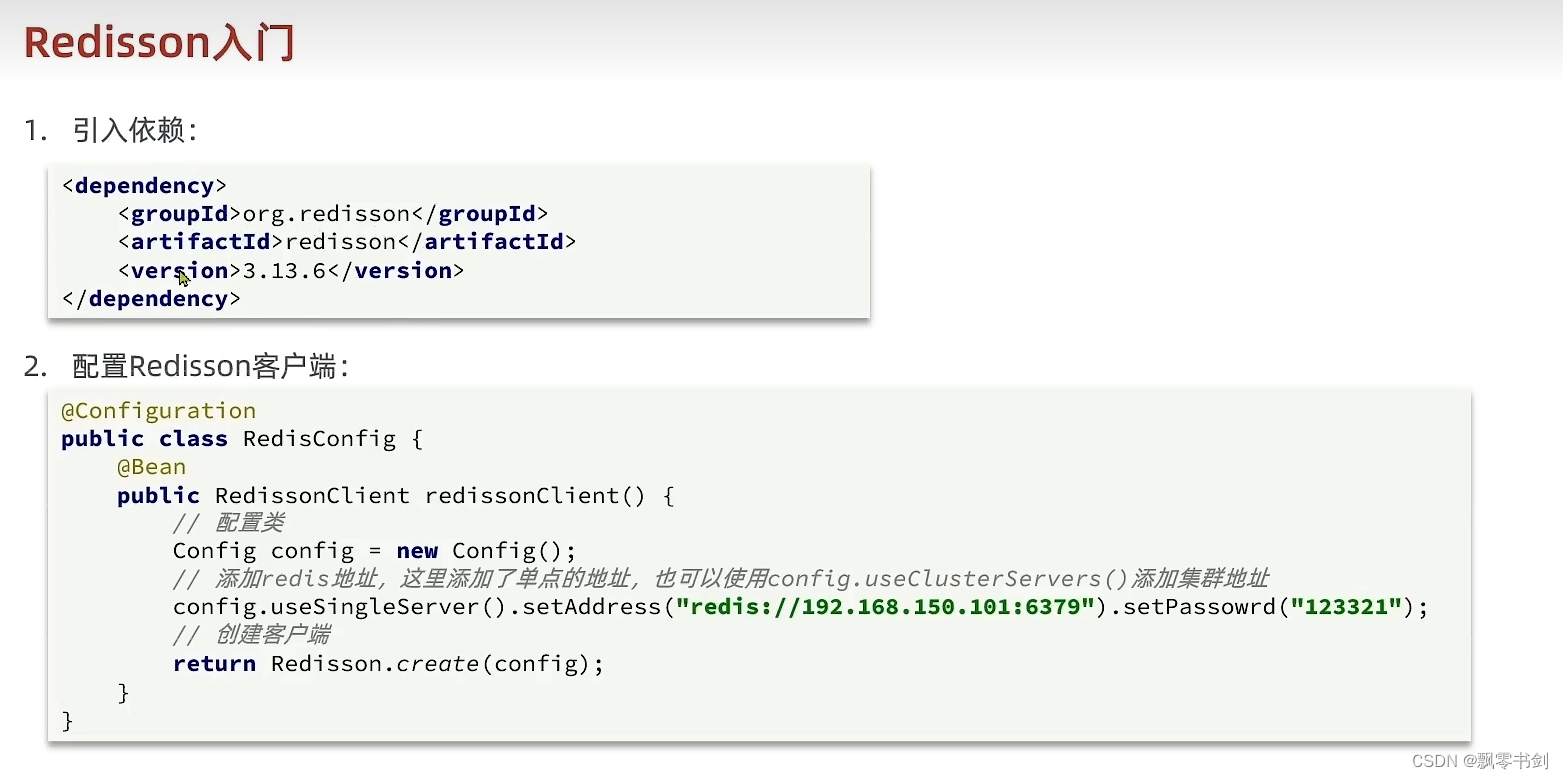
Redis学习总结
Redis学习总结 文章目录 Redis学习总结Radis基本介绍docker的安装基本数据结构通用命令字符型key的层次结构Hash类型Listset sortedset集合redis的java客户端jedis的使用jedis连接池的配置 SpringDataRedis自定义redistemplate的序列化与反序列化方式stringtemplate的使用 redi…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
