当前位置： 首页 > news >正文

JVM GC ROOT分析

news 2026/2/8 17:27:51


GC root原理：通过对枚举GCroot对象做引用可达性分析，即从GC root对象开始，向下搜索，形成的路径称之为 引用链。如果一个对象到GC roots对象没有任何引用，没有形成引用链，那么该对象等待GC回收，换而言之，如果减少内存泄漏，也就是切断引用链,常见的GCRoot对象如下：

1、虚拟机栈中的本地变量
能成为 GC Root，譬如各个线程被调用的方法堆栈中使用到的参数、局部变量、临时变量，

那么这个是什么？这个不就是我们在栈针中看到的这个吗？

 

那么为什么他能成GCROOT呢？或者他为什么能成为指向的依据呢？

我这个局部变量表为什么存在，因为他有栈针存在，因为栈针中有局部变量表的存在。

那么然后呢，栈针又为什么存在？

它对应的是一个方法的执行，那么然后呢？

他既然是对应一个方法的执行的话，说明有线程在调用这个方法。也就意味着线程中（栈针）的局部变量正在使用着。如果把它称之为GC ROOT的候选者的话，我认为是合适的，因为如果把这里局部变量比如op2,为什么能够成为，因为他被正在引用着。这个对象又有可能在引用其他对象，然后被引用的其他对象又有可能在引用其他对象，只要由op2这个对象去触发，能够去找到最终的一个对象，假如你有一个对象preson.这个对象经过由op2触发的对象。这个就能称之为我

相关文章：

JVM GC ROOT分析

GC root原理：通过对枚举GCroot对象做引用可达性分析，即从GC root对象开始，向下搜索，形成的路径称之为 引用链。如果一个对象到GC roots对象没有任何引用，没有形成引用链，那么该对象等待GC回收，换而言之，如果减少内存泄漏，也就是切断引用链,常见的GCRoot对象如下： 1、…...

编程日记 2023/8/4 11:10:03

记一道有趣的sql题

有一张运单表：dwd_biz_waybill_td，该表的主键是way_bill_id，并且有如下字段： way_bill_id（运单表主键），shiping_date（下单日期，时间格式为yyyy-MM-dd）&#…...

编程日记 2023/8/4 11:09:02

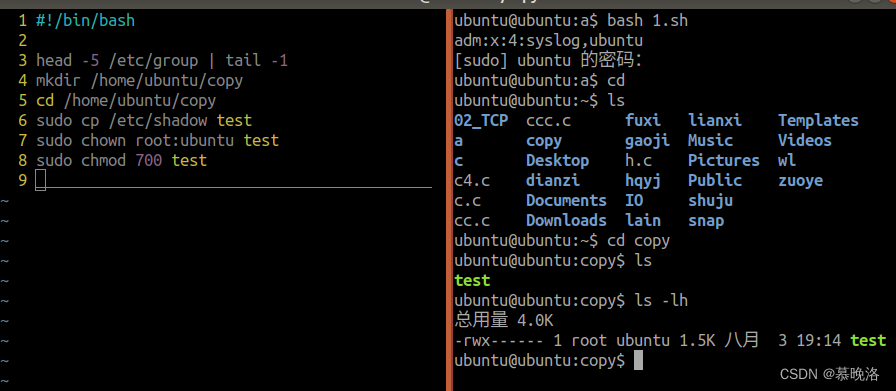
C高级【day2】

思维导图&#xff1a; 递归实现&#xff0c;输入一个数&#xff0c;输出这个数的每一位&#xff1a; #include<myhead.h>//递归函数 void fun(int num){//num没值不再递归if(0 num){return;}//输出数的最后一位printf("%d\t", num%10);//递归fun(num/10);}…...

编程日记 2023/8/4 11:08:01

认识Webpack插件Plugin；CleanWebpackPlugin插件；HtmlWebpackPlugin；DefinePlugin；Mode模式

目录 1_认识插件Plugin2_CleanWebpackPlugin3_HtmlWebpackPlugin4_DefinePlugin4.1_介绍4.2_DefinePlugin的使用 5_Mode模式 1_认识插件Plugin Webpack的另一个核心是Plugin&#xff0c;官方有这样一段对Plugin的描述&#xff1a; While loaders are used to transform certai…...

编程日记 2023/8/4 11:07:00

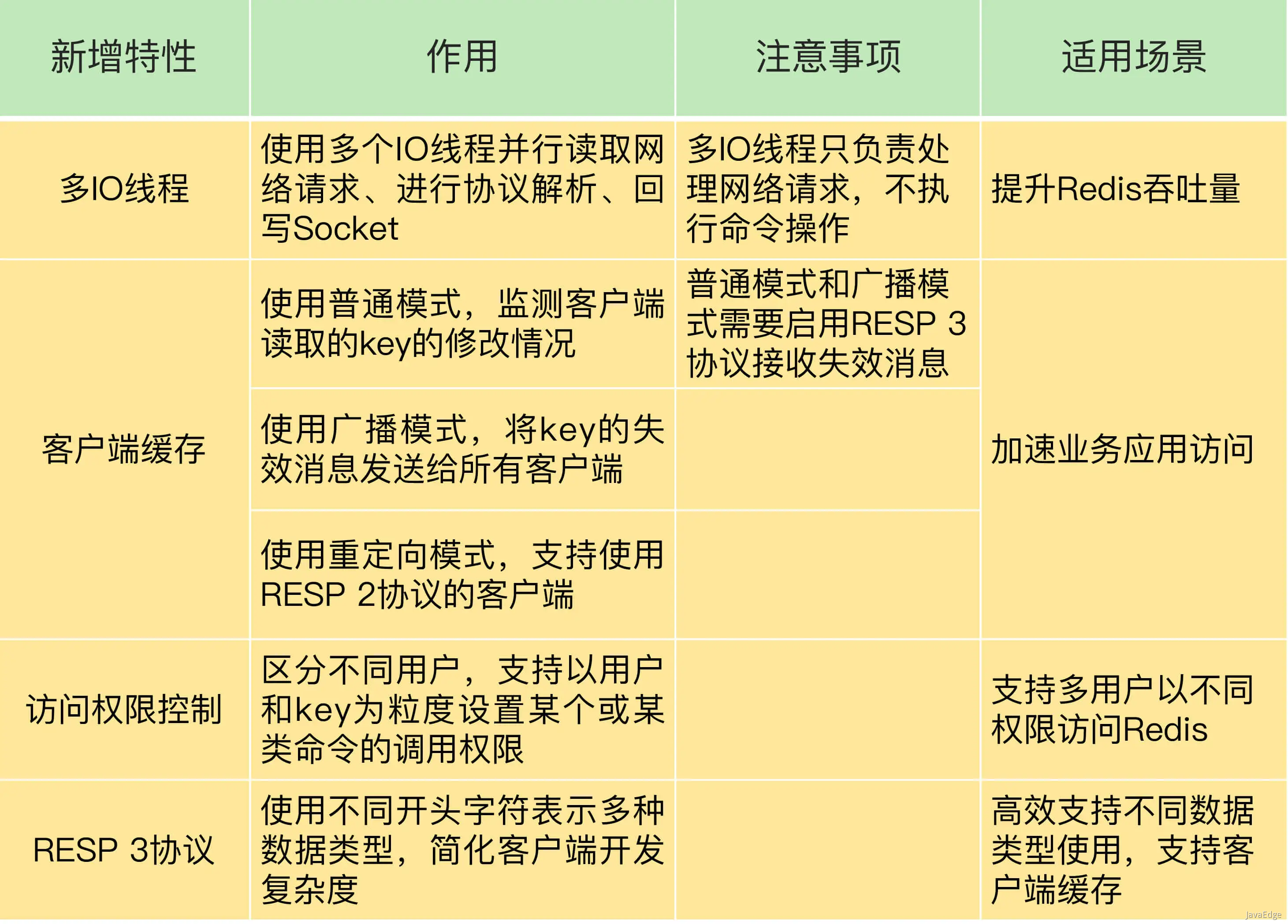
Redis 6.0的新特性：多线程、客户端缓存与安全

2020年5月份&#xff0c;6.0版本。 面向网络处理的多IO线程可以提高网络请求处理的速度&#xff0c;而客户端缓存可以让应用直接在客户端本地读取数据&#xff0c;这两个特性可以提升Redis的性能。 细粒度权限控制让Redis可以按照命令粒度控制不同用户的访问权限&#xff0c;…...

编程日记 2023/8/4 11:05:59

【雕爷学编程】MicroPython动手做（37）——驱动LCD与图文显示3

MixPY——让爱(AI)触手可及 MixPY布局 主控芯片&#xff1a;K210&#xff08;64位双核带硬件FPU和卷积加速器的 RISC-V CPU&#xff09; 显示屏&#xff1a;LCD_2.8寸 320*240分辨率&#xff0c;支持电阻触摸 摄像头&#xff1a;OV2640&#xff0c;200W像素 扬声器&#…...

编程日记 2023/8/4 11:04:58

自然语言处理从入门到应用——LangChain：提示（Prompts）-[提示模板：序列化提示信息]

分类目录&#xff1a;《自然语言处理从入门到应用》总目录 将提示信息存储为文件而不是Python代码通常更好。这样可以方便共享、存储和版本控制提示信息。本文介绍了如何在LangChain中进行提示信息的序列化&#xff0c;包括不同类型的提示信息和不同的序列化选项。 在高层次上…...

编程日记 2023/8/4 11:03:57

【LinearAlgebra】Chapter 12 - Linear Algebra in Probability Statistics

文章目录 Chapter 12 - Linear Algebra in Probability & StatisticsVariance (around athe mean) 方差&#xff08;接近均值&#xff09;Continuous Probability Distributions 连续概率分布Mean and Variance of p ( x ) p(x) p(x) p ( x ) p(x) p(x) 的均值和方差Norm…...

编程日记 2023/8/4 11:02:56

webshell详解

Webshell详解 一、 Webshell 介绍二 、 基础常见webshell案例 一、 Webshell 介绍 概念 webshell就是以asp、php、jsp或者cgi等网页文件形式存在的一种命令执行环境&#xff0c;也可以将其称做为一种网页后门。黑客在入侵了一个网站后&#xff0c;通常会将asp或php后门文件与…...

编程日记 2023/8/4 11:01:54

数据结构 | 搜索和排序——搜索

目录 一、顺序搜索 二、分析顺序搜索算法 三、二分搜索 四、分析二分搜索算法 五、散列 5.1 散列函数 5.2 处理冲突 5.3 实现映射抽象数据类型 搜索是指从元素集合中找到某个特定元素的算法过程。搜索过程通常返回True或False&#xff0c;分别表示元素是否存在。有时&a…...

编程日记 2023/8/4 11:00:53

【python】对象

对象 初识对象成员方法类和对象构造方法其它内置方法封装继承类型注释多态综合案例二级目录三级目录 初识对象 设计表格-生产表格-填写表格 对应于程序中&#xff1a;设计类-创建对象-对象属性赋值 class Student:nameNonegenderNone # 基于类创建对象 stu_1Student() stu_2S…...

编程日记 2023/8/4 10:59:52

k8s概念-污点与容忍

k8s 集群中可能管理着非常庞大的服务器&#xff0c;这些服务器可能是各种各样不同类型的&#xff0c;比如机房、地理位置、配置等&#xff0c;有些是计算型节点&#xff0c;有些是存储型节点&#xff0c;此时我们希望能更好的将 pod 调度到与之需求更匹配的节点上。 此时就需要…...

编程日记 2023/8/4 10:58:49

“从零开始学习Spring Boot：构建高效、可扩展的Java应用程序“

标题&#xff1a;从零开始学习Spring Boot&#xff1a;构建高效、可扩展的Java应用程序 简介&#xff1a; Spring Boot是一种用于简化Java应用程序开发的开源框架&#xff0c;它提供了一种快速、高效的方式来构建可扩展的应用程序。本文将介绍如何从零开始学习Spring Boot&…...

编程日记 2023/8/4 10:57:48

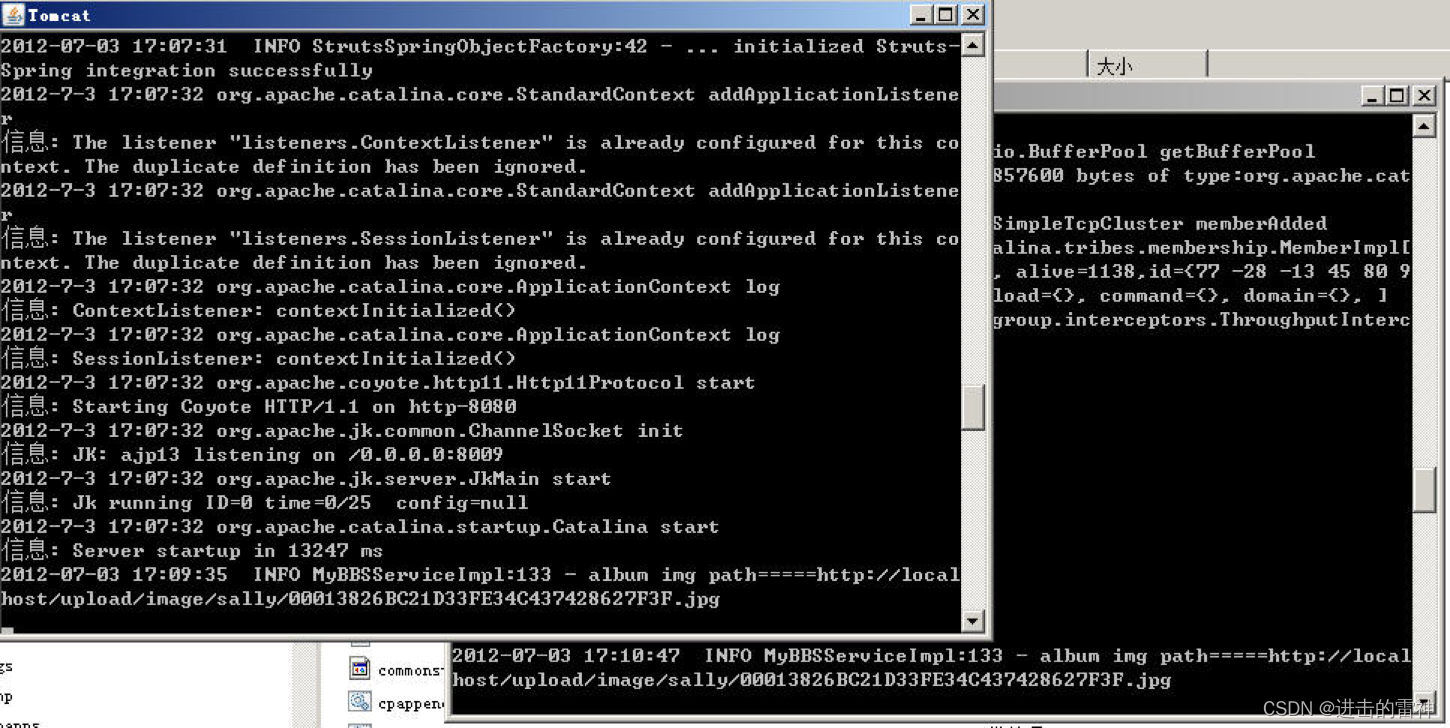
通向架构师的道路之tomcat集群

一、为何要集群 单台App Server再强劲&#xff0c;也有其瓶劲&#xff0c;先来看一下下面这个真实的场景。 当时这个工程是这样的&#xff0c;tomcat这一段被称为web zone&#xff0c;里面用springws&#xff0c;还装了一个jboss的规则引擎Guvnor5.x&#xff0c;全部是ws没有se…...

编程日记 2023/8/4 10:56:47

结构体，枚举，联合大小的计算规则

目录 1.结构体大小的计算 补充&#xff08;位段&#xff09; 2.枚举的大小&#xff08;4个字节&#xff09; 3.联合大小的计算 1.结构体大小的计算 &#xff08;1&#xff09;结构体内存对齐的规则 1. 第一个成员在与结构体变量偏移量为 0 的地址处。 2. 其他成员变量要对…...

编程日记 2023/8/4 10:55:46

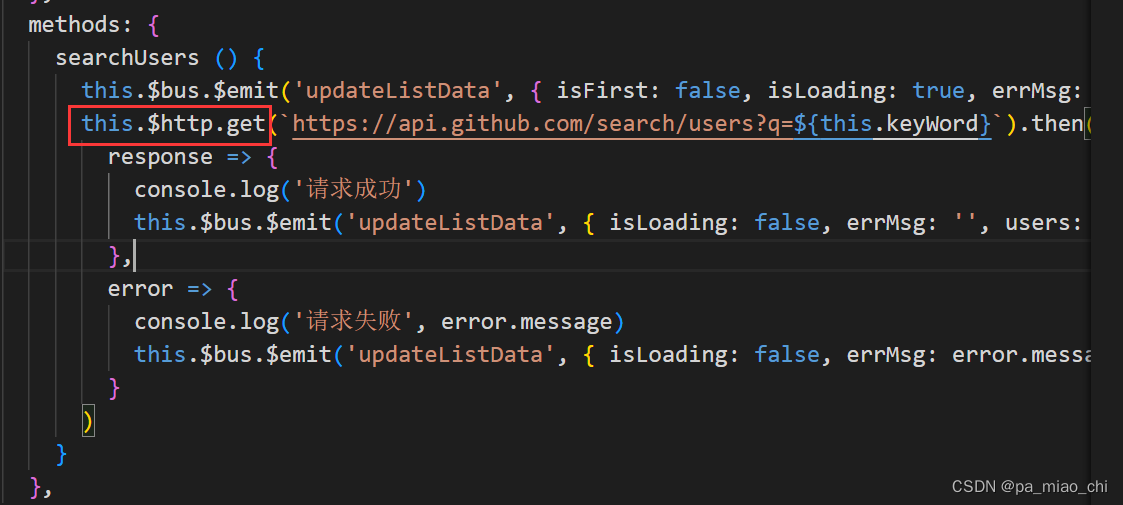
Vue2 第十七节 Vue中的Ajax

1.Vue脚手架配置代理 2.vue-resource 一.Vue脚手架配置代理 1.1 使用Ajax库 -- axios ① 安装 : npm i axios ② 引入: import axios from axios ③ 使用示例 1.2 解决开发环境Ajax跨域问题 跨域&#xff1a;违背了同源策略&#xff0c;同源策略规定协议名&#xff0…...

编程日记 2023/8/4 10:54:44

ES6 - 字符串新增的一些常用方法

文章目录 0&#xff0c;新增的一些方法1&#xff0c;includes()、startsWith()、endsWith()2&#xff0c;repeat()3&#xff0c;padStart()、padEnd()4&#xff0c;trimStart()、trimEnd()5&#xff0c;replaceAll()6&#xff0c;at() 0&#xff0c;新增的一些方法 介绍一些ES6…...

编程日记 2023/8/4 10:53:43

最新SQLMap安装与入门技术

点击星标&#xff0c;即时接收最新推文 本文选自《web安全攻防渗透测试实战指南&#xff08;第2版&#xff09;》 五折购买链接&#xff1a;u.jd.com/3ibjeF6 SQLMap详解 SQLMap是一个自动化的SQL注入工具&#xff0c;其主要功能是扫描、发现并利用给定URL的SQL注入漏洞。SQLMa…...

编程日记 2023/8/4 10:52:42

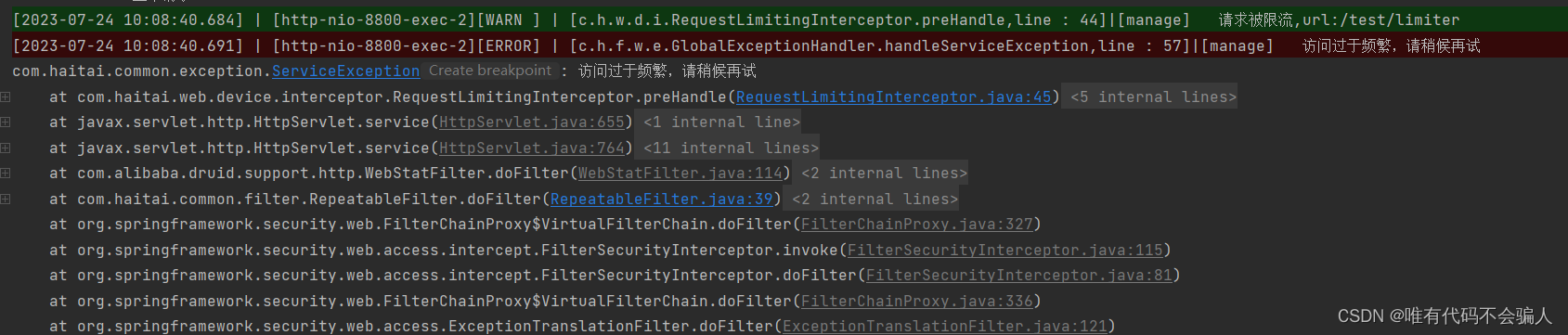
Java 使用 Google Guava 实现接口限流

一、引入依赖 <dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>30.0-jre</version> </dependency>二、自定义注解及限流拦截器 自定义注解&#xff1a;Limiter package com.haita…...

编程日记 2023/8/4 10:51:41

帮助中心的价值是什么？怎样才能在线搭建官网网站帮助中心？

帮助中心&#xff08;Help Center&#xff09;是一个提供公司或组织产品或服务相关信息的在线平台。它的价值在于为用户提供便捷的自助服务和解决问题的渠道&#xff0c;同时也能减轻客服人员的负担。 如何在线搭建官网网站帮助中心的步骤 确定需求&#xff1a;在搭建帮助中心…...

编程日记 2023/8/4 10:50:40

wordpress后台更新后 前端没变化的解决方法

使用siteground主机的wordpress网站&#xff0c;会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后&#xff0c;网站没有变化的情况。 不熟悉siteground主机的新手&#xff0c;遇到这个问题&#xff0c;就很抓狂&#xff0c;明明是哪都没操作错误&#x…...

编程新知 2026/2/7 23:18:37

Python爬虫实战：研究MechanicalSoup库相关技术

一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库，专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力，提供了直观的 API，让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

编程新知 2025/10/10 18:13:55

零门槛NAS搭建：WinNAS如何让普通电脑秒变私有云？

一、核心优势&#xff1a;专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发&#xff0c;是一款收费低廉但功能全面的Windows NAS工具&#xff0c;主打“无学习成本部署” 。与其他NAS软件相比&#xff0c;其优势在于&#xff1a; 无需硬件改造&#xff1a;将任意W…...

编程新知 2026/1/2 23:01:24

3.3.1_1 检错编码（奇偶校验码）

从这节课开始&#xff0c;我们会探讨数据链路层的差错控制功能&#xff0c;差错控制功能的主要目标是要发现并且解决一个帧内部的位错误&#xff0c;我们需要使用特殊的编码技术去发现帧内部的位错误&#xff0c;当我们发现位错误之后&#xff0c;通常来说有两种解决方案。第一…...

编程新知 2026/1/30 3:28:14

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?

论文网址&#xff1a;pdf 英文是纯手打的&#xff01;论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误&#xff0c;若有发现欢迎评论指正&#xff01;文章偏向于笔记&#xff0c;谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

编程新知 2026/2/6 14:42:11

如何为服务器生成TLS证书

TLS&#xff08;Transport Layer Security&#xff09;证书是确保网络通信安全的重要手段&#xff0c;它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书&#xff0c;可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

编程新知 2025/12/17 5:54:30

今日科技热点速览

&#x1f525; 今日科技热点速览 &#x1f3ae; 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售&#xff0c;主打更强图形性能与沉浸式体验&#xff0c;支持多模态交互&#xff0c;受到全球玩家热捧 。 &#x1f916; 人工智能持续突破 DeepSeek-R1&…...

编程新知 2025/11/20 14:26:29

select、poll、epoll 与 Reactor 模式

在高并发网络编程领域&#xff0c;高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表&#xff0c;以及基于它们实现的 Reactor 模式&#xff0c;为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。​ 一、I…...

编程新知 2026/2/8 6:37:36

CMake控制VS2022项目文件分组

我们可以通过 CMake 控制源文件的组织结构，使它们在 VS 解决方案资源管理器中以“组”（Filter）的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总（共4种） 方法描述是否推荐…...

编程新知 2025/12/4 15:47:17

大数据学习（132）-HIve数据分析

​​​​&#x1f34b;&#x1f34b;大数据学习&#x1f34b;&#x1f34b; &#x1f525;系列专栏&#xff1a; &#x1f451;哲学语录: 用力所能及&#xff0c;改变世界。 &#x1f496;如果觉得博主的文章还不错的话&#xff0c;请点赞&#x1f44d;收藏⭐️留言&#x1f4…...

编程新知 2025/10/7 8:52:21