【Leetcode】二叉树的最近公共祖先,二叉搜索树转换成排好序的双向链表,前序遍历与中序遍历构造二叉树
一.二叉树的最近公共祖先
链接
二叉树的最近公共祖先
题目再现

『Ⅰ』思路一:转换成相交链表问题

观察上图,节点1和节点4的最近公共祖先是3,这是不是很像相交链表的问题,关于相交链表,曾经我在另一篇文章里写到过,读者可以参考:反转链表 合并链表 相交链表
但是要转换成相交链表,就要从后向前遍历,如果节点中还存在一个指针,指向父节点就好了,这种结构其实叫三叉链结构:
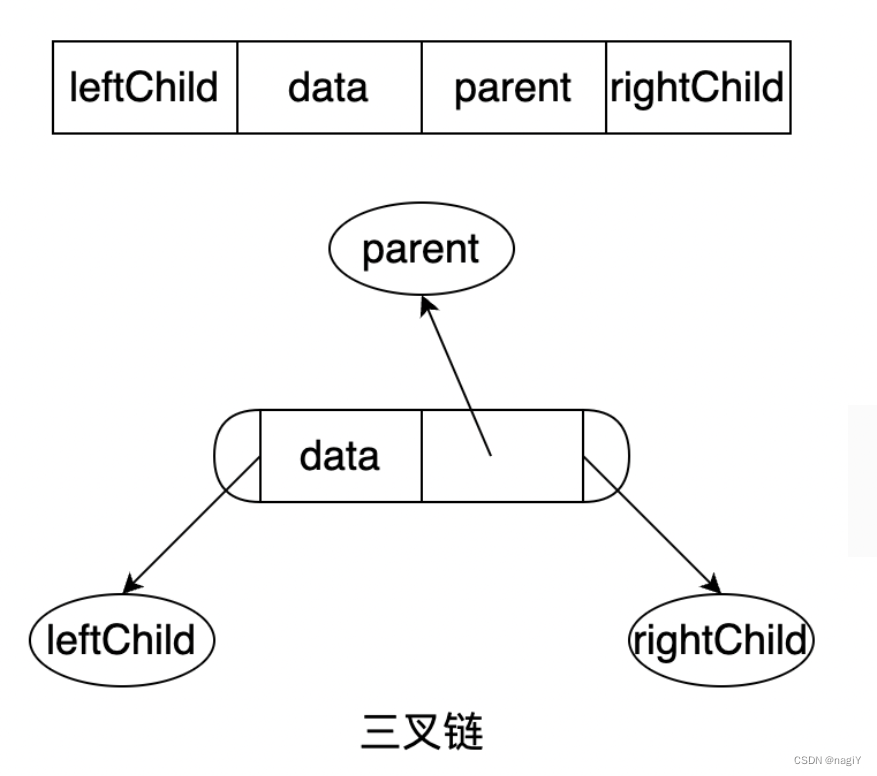
但是这题给我们的只是一个普通的二叉树,没有三叉链,那该怎么办呢?
那么就转换为第二种思路:寻找节点的祖先路径
『Ⅱ』思路二:寻找节点的祖先路径
我们可以把要找的两个节点的路径找出来,然后存到栈里,这样把两个节点的祖先路径找出来后,就可以转换成链表相交问题了。
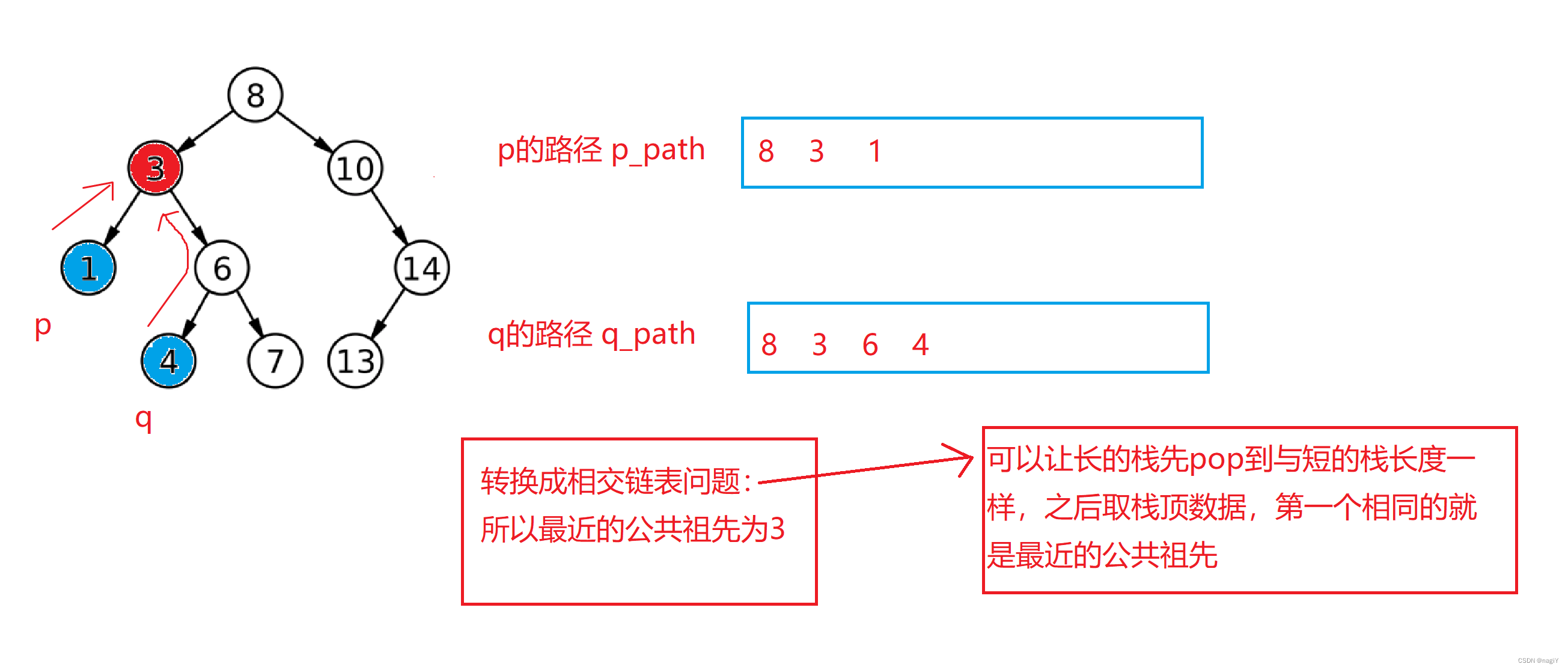
关于该怎么入栈:
我们先让节点入栈,然后判断它是否等于我们要找的节点,如果是,则返回true;如果不是,则
1.如果左节点不为空,返回true;
2.如果右节点不为空,返回true;
3.如果左右节点都为空,则pop掉栈顶的元素,返回false;
完整代码:
class Solution {
public:bool findpath(TreeNode*cur,TreeNode*x,stack<TreeNode*>&path) //注意这里要传引用{if(cur==nullptr)return false;path.push(cur);if(cur==x)return true;if(findpath(cur->left,x,path))return true;if(findpath(cur->right,x,path))return true;path.pop();return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {stack<TreeNode*> ppath;stack<TreeNode*> qpath;findpath(root,p,ppath);findpath(root,q,qpath);while(ppath.size()>qpath.size()) //使两个栈一样长{ppath.pop();}while(ppath.size()<qpath.size()){qpath.pop();}while(ppath.top()!=qpath.top()) //从栈顶开始,寻找第一个相同的数据{ppath.pop();qpath.pop();}return ppath.top();}
}; 
可以看到,这种方法效率使非常高的,它的时间复杂度是O(N);
『Ⅲ』思路三:暴力查找
其实当两个节点分别在左树和右树时,它们最近的公共祖先就是根节点,如果不在树两边,而是都在左树,或是都在右树,那么就可以转化成子问题,递归解决。
如下图:
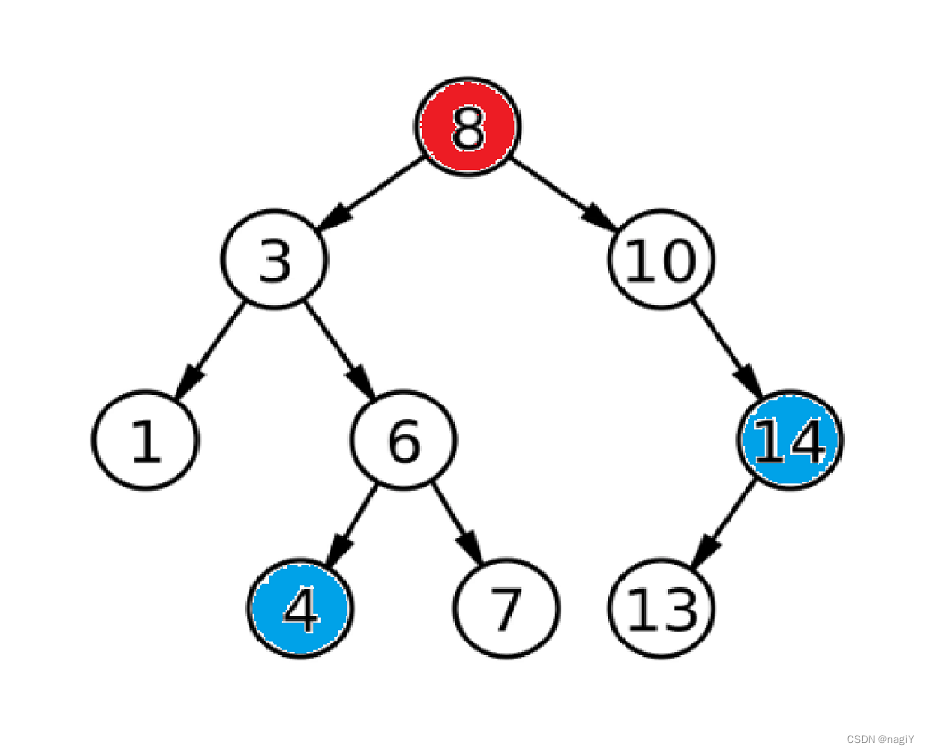
注意,如果有一个节点恰好是根节点,那么这个节点就是最近的公共祖先,也是说一个节点的祖先也算它自己。
如下图:

那么该怎么判断节点是在左树还是右树呢?
我们可以定义四个布尔变量,分别是:pinleft(p在左树) pinright(p在右树)
qinleft (q在左树 ) qinright(q在右树)
哪个布尔值为真就表明这个节点在哪边。
完整代码:
class Solution {
public:bool find(TreeNode*cur,TreeNode*x){if(cur==nullptr)return false;return cur==x||find(cur->left,x)||find(cur->right,x);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode*q) {if(root==nullptr)return nullptr;if(root==p||root==q) //某一个节点为根return root;bool pinleft,pinright;bool qinleft,qinright;pinleft=find(root->left,p); //去左树寻找p节点pinright=!pinleft;qinleft=find(root->left,q); //去左树寻找q节点qinright=!qinleft;if(pinleft&&qinleft) //都在左树转化成子问题return lowestCommonAncestor(root->left,p,q);else if(pinright&&qinright) //都在右树转化成子问题return lowestCommonAncestor(root->right,p,q);else //分别在左树和右树return root;}
};
可以看到,这个算法的效率是很差的,它的时间复杂度是O(N^2)。
二.二叉搜索树转换成排好序的双向链表
链接
二叉搜索树转换成排好序的双向链表
题目再现

解法
根据题意,原二叉搜索树的左指针就是双链表的前驱指针,右指针就是双链表的后继指针;
而且本题还要求空间复杂度是O(1),也就是说不能额外开空间,其实要是能额外开空间,那么这题就非常简单了。
我们知道,二叉搜索树的中序遍历结果是升序列,这恰好满足了题目排好序的要求;
那要怎么在原树上操作,使它转换成双链表呢?
举个例子:
对于我们过去(prev)的事,现在(cur)的我们肯定是一清二楚的,而且是可以确定的,但未来(next)的事并不能确定;
但如果我们是从未来穿越回现在的,那么穿越回来的我们,就可以确定未来的事。所以说过去(prev)的未来(next)就是现在(cur)。
回到题目,所以cur的左指针(left)就是双链表的前驱(prev),prev的右指针就是后继(next),然后再更新一下prev即可。
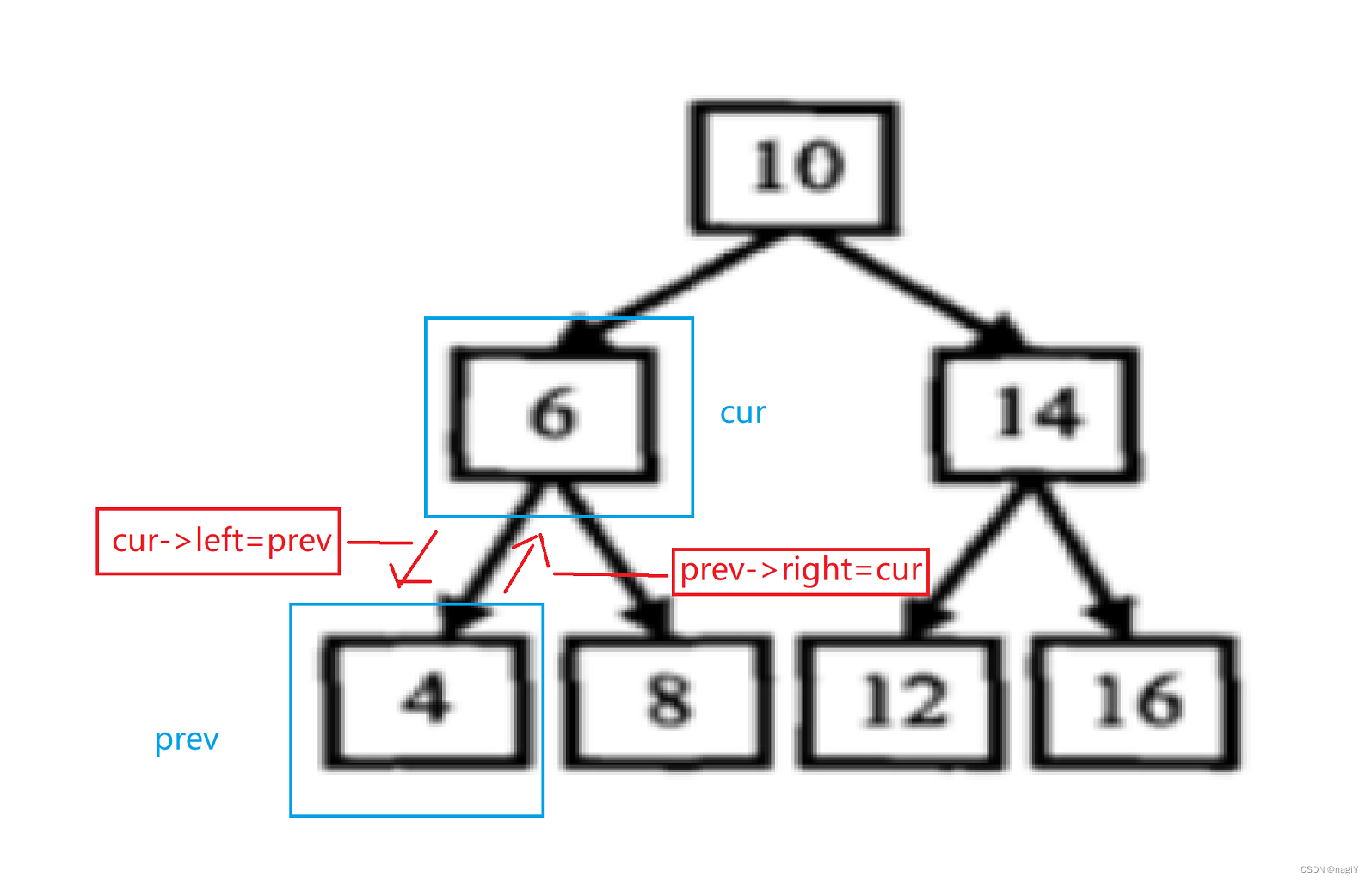
完整代码:
class Solution {
public:void InOrder(TreeNode*cur,TreeNode*&prev) //注意要传引用{if(cur==nullptr)return;InOrder(cur->left,prev);cur->left=prev; //cur的左指针就是previf(prev) //注意判断prev是否为空prev->right=cur; //prev的右指针就是curprev=cur; //更新prevInOrder(cur->right,prev);}TreeNode* Convert(TreeNode* pRootOfTree) {if(pRootOfTree==nullptr)return nullptr;TreeNode*prev=nullptr; //定义一个前驱指针InOrder(pRootOfTree,prev); //中序遍历TreeNode*head=pRootOfTree;while(head->left) //最左边的节点即为双链表的头{head=head->left;}return head;}
};三.根据一棵树的前序遍历与中序遍历构造二叉树
链接
根据一棵树的前序序列与中序序列构建二叉树
题目再现
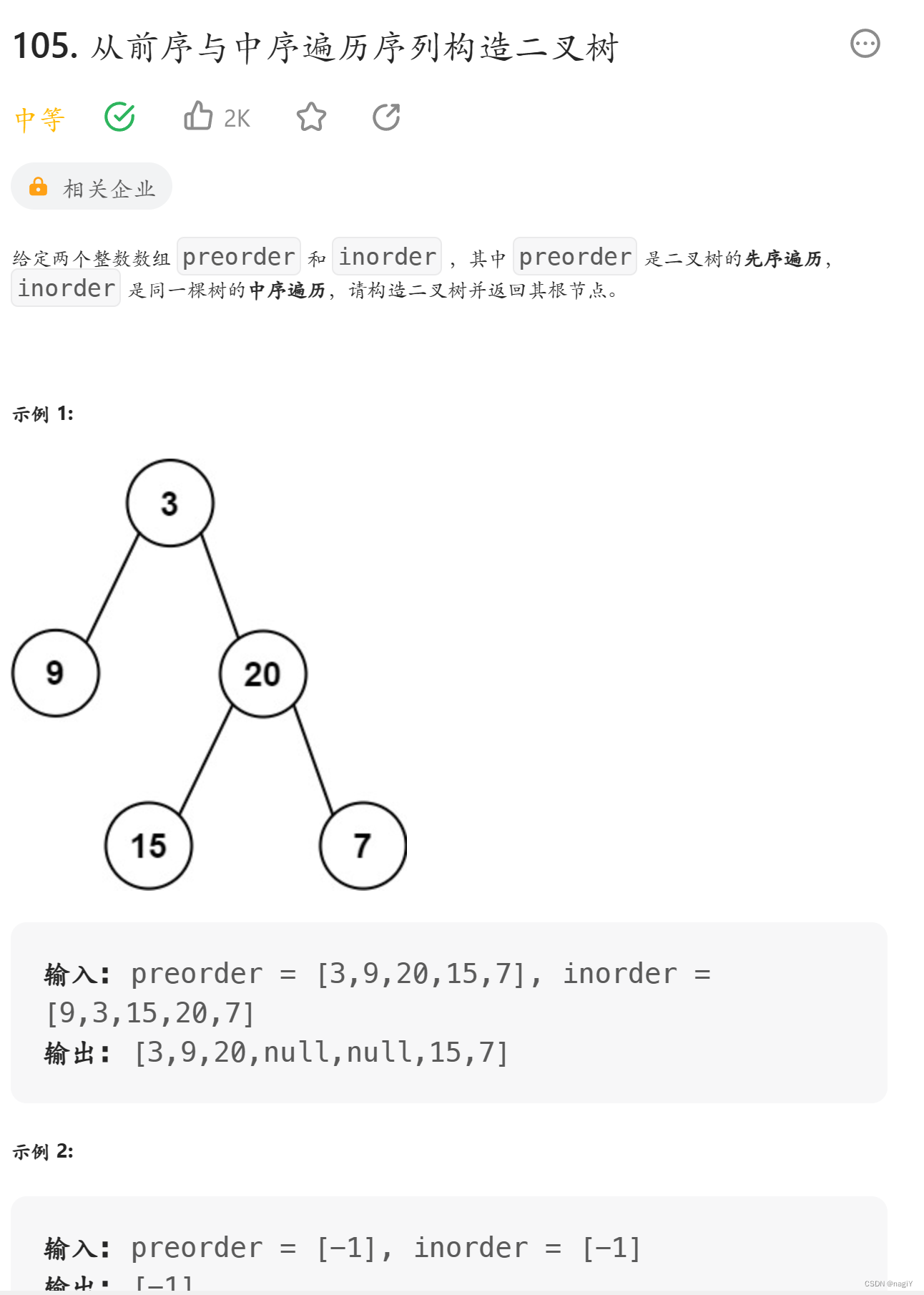
解法
众所周知,前序遍历的顺序为:根 左 右
中序遍历的顺序为:左 根 右
所以根据前序序列就可以确定根,确定了根后就可以分成左子树和右子树;
确定好根后,根据中序序列就可以分割左子树和右子树的区间,然后构建树;
而左子树或是右子树也有根,这样就可以转化成子问题,递归实现,但要注意,前序序列中的每个数只能使用一次。
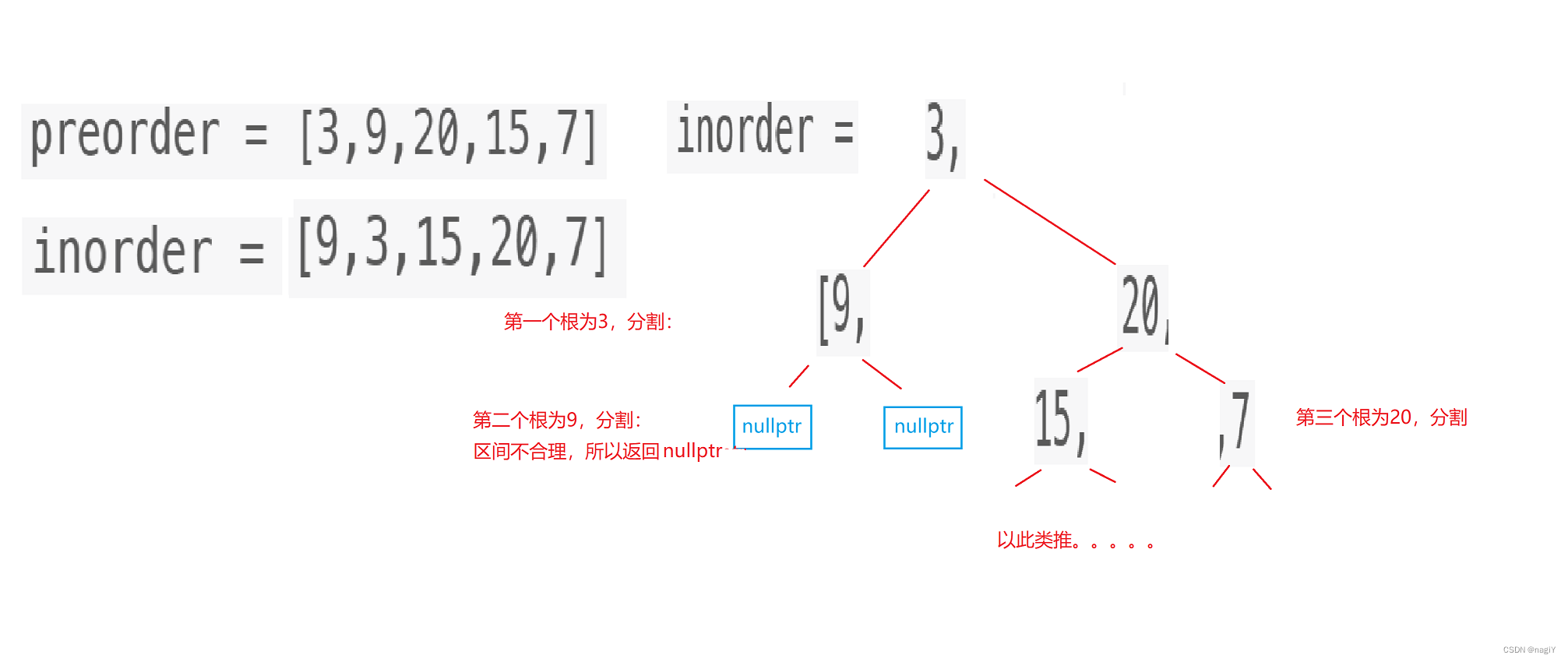
完整代码:
class Solution {
public://注意这个prei用于遍历前序序列数组,因为每个数只能用一次,所以要传引用TreeNode*_build(vector<int>& preorder, vector<int>& inorder,int &prei,int inbegin,int inend){if(inbegin>inend) //当区间不存在时返回空指针return nullptr;TreeNode*preroot=new TreeNode(preorder[prei]);int rooti=inbegin; //找根在中序序列中的位置while(rooti<=inend){if(preorder[prei]==inorder[rooti]) //找到后跳出循环break;rooti++;}prei++; //本次确定好根后,prei++找下一个根//分割区间,递归构建//[inbegin,rooti-1] rooti [rooti+1,inend]preroot->left=_build(preorder,inorder,prei,inbegin,rooti-1);preroot->right=_build(preorder,inorder,prei,rooti+1,inend);return preroot;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int i=0;return _build(preorder,inorder,i,0,inorder.size()-1);}
};🐬🤖本篇文章到此就结束了, 若有错误或是建议的话,欢迎小伙伴们指出;🕊️👻
😄😆希望小伙伴们能支持支持博主啊,你们的支持对我很重要哦;🥰🤩
😍😁谢谢你的阅读。😸😼
相关文章:

【Leetcode】二叉树的最近公共祖先,二叉搜索树转换成排好序的双向链表,前序遍历与中序遍历构造二叉树
一.二叉树的最近公共祖先 链接 二叉树的最近公共祖先 题目再现 『Ⅰ』思路一:转换成相交链表问题 观察上图,节点1和节点4的最近公共祖先是3,这是不是很像相交链表的问题,关于相交链表,曾经我在另一篇文章里写到过&a…...

途乐证券|互联金融概念爆发,安硕信息“20cm”涨停,高伟达等大涨
互联金融概念4日盘中强势拉升,截至发稿,安硕信息“20cm”涨停,高伟达、卓创资讯、慧博云通涨超12%,恒银科技、极点软件亦涨停,指南针涨超9%,金证股份涨逾7%。 高伟达昨日在投资者互动平台表明,公…...
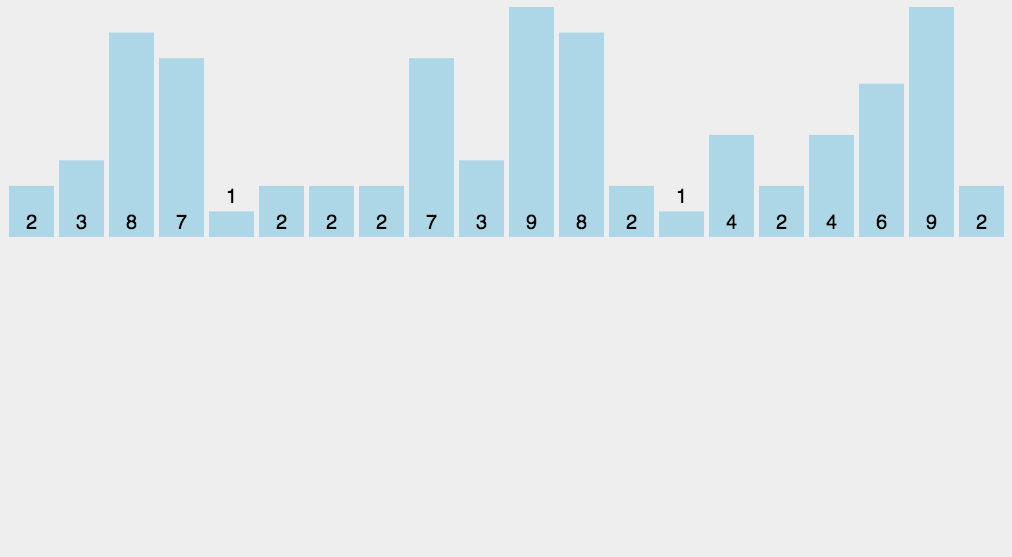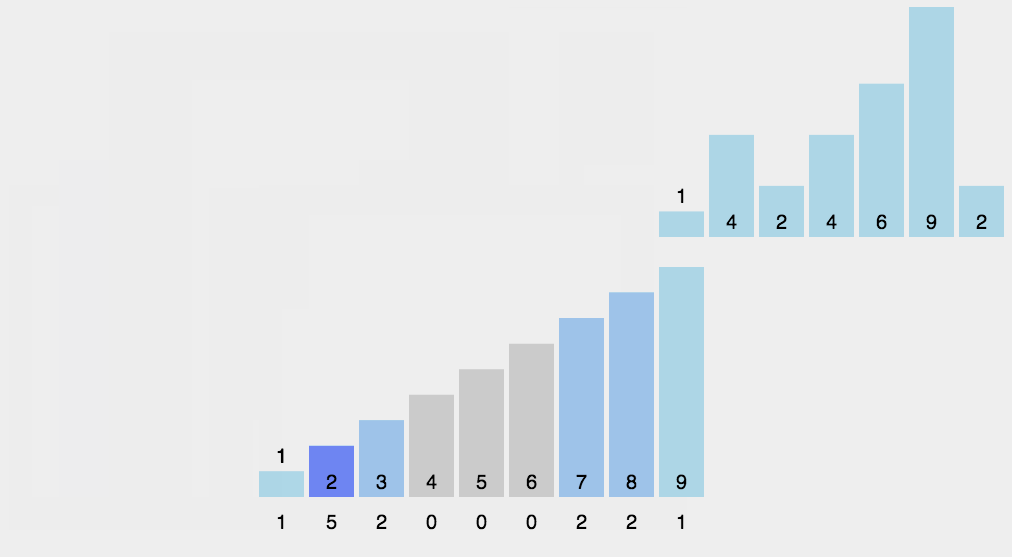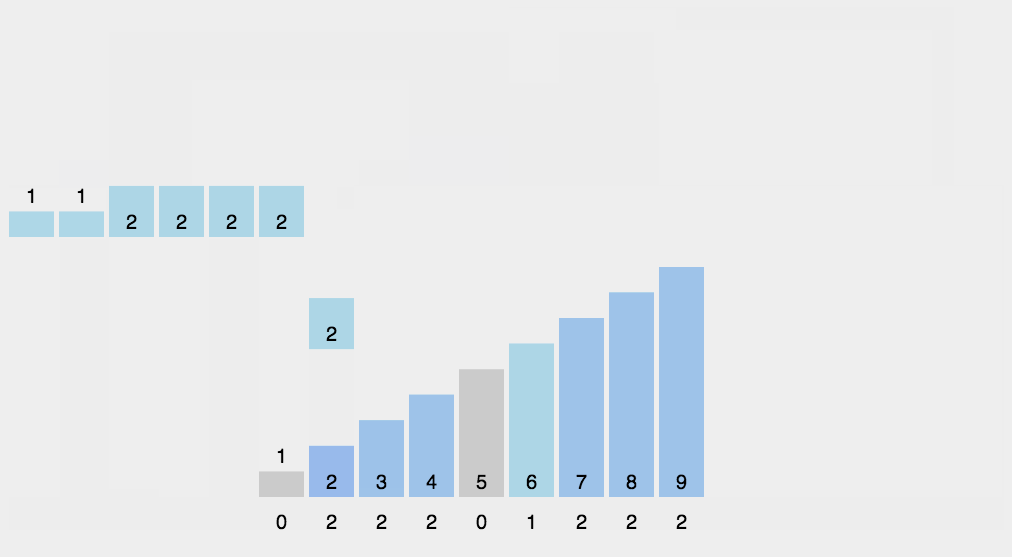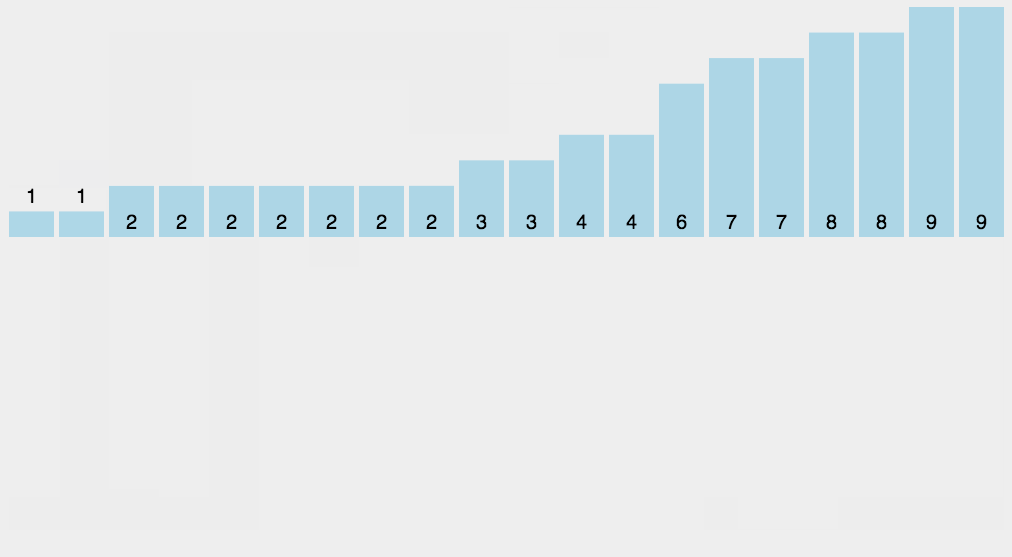
计数排序算法
计数排序 计数排序说明: 计数排序(Counting Sort)是一种非比较性的排序算法,它通过统计元素出现的次数,然后根据元素出现的次数将元素排列在正确的位置上,从而实现排序。计数排序适用于非负整数或者具有确…...

企业高性能web服务器-nginx
1.nginx简介: nginx是企业高可用的web服务器,nginx也可用来做反向代理服务器器,具有高并发,占用资源少,功能丰富,也可以作为简单的负载均衡。 nginx在企业中的功能: web服务软件 反向代理服务器…...
GaussDB数据库的元数据及其管理简介
目录 一、前言 二、元数据简介 1、元数据定义 2、元数据分类 3、数据库元数据管理 三、GaussDB数据库的元数据管理 1、GaussDB数据库的元数据管理 2、通过“SQL 系统表/系统视图/系统函数”的方式管理(采集)元数据 1)获取表、视图及…...

合并两个有序链表 LeetCode热题100
题目 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 思路 遍历两个链表比较大小,按从小到大添加到链表即可。 代码 /*** Definition for singly-linked list.* struct ListNode {* int val;* List…...
【C++】模拟实现string
目录 🌞专栏导读 🌛定义string类 🌛构造函数 🌛拷贝构造函数 🌛赋值函数 🌛析构函数 🌛[]操作符重载 🌛c_str、size、capacity函数 🌛比较运算符重载 &#…...

AI智慧安监视频监控汇聚平台EasyCVR调用接口出现跨域现象该如何解决?
视频监控汇聚EasyCVR可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有GB28181、RTSP/Onvif、RTMP等,以及厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等,能对外分发RTSP、RTMP、FLV、HLS、WebRTC等格式的视…...

无人机机巢有哪些,无人机机场/机场的主要分类
随着无人机技术的飞速发展,无人机已经渗透到了物流、农业、救援、公共安全等多个领域。而为了使这些无人机能更加高效、灵活地运行,一个新的概念应运而生,那就是无人机机巢(UAV Nest)。复亚智能无人机机巢是一种供无人…...

联想存储 HH0305_DE4000H 划分卷组、卷、主机
创建卷组 可使用卷组来创建可供主机访问的一个或多个卷。卷组是具有共同特性(如 RAID 级别和容量)的卷的容器。 关于本任务 如果拥有容量较大的驱动器且可以在控制器之间分发卷,则为每个卷组创建多个卷可以很好地利用存储容量和保护数据。…...
【Python机器学习】实验08 决策树
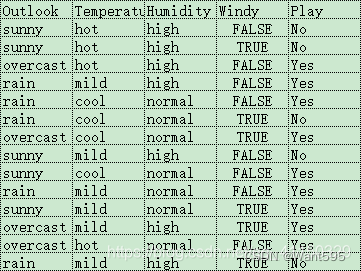
文章目录 决策树1 创建数据2 定义香农信息熵3 条件熵4 信息增益5 计算所有特征的信息增益,选择最优最大信息增益的特征返回6 利用ID3算法生成决策树7 利用数据构造一颗决策树Scikit-learn实例决策树分类决策树回归Scikit-learn 的决策树参数决策树调参 实验1 通过sk…...

MySQL的innoDB存储引擎如何解决幻读的问题?
MySQL的innoDB存储引擎如何解决幻读的问题 基本情况 MySQL有四种事务隔离级别,这四种隔离级别代表当存在多个事务并发冲突时,可能出现的脏读、不可重复读、幻读的问题InnoDB 在 RR 的隔离级别下 ,解决了幻读的问题幻读是指在同一个事务中&a…...

Web3.0:重新定义互联网的未来
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! Web3.0:重新定义互联网的未来 Web3.0是指下一代互联网,也称为“分布式互联网”。相比于Web1.0和Web2.0,Web3.0具有更强的去中心化、…...

2023年还能选择前端吗?
前言 在Github2022的 Octoverse年度报告上,稳居最多使用榜首的语言可以看到是JavaScript,作为前端中最为关键的一部分,这说明即使现在,前端这一块仍然是大量的人涌进来,依然是火热,但是,一门语…...
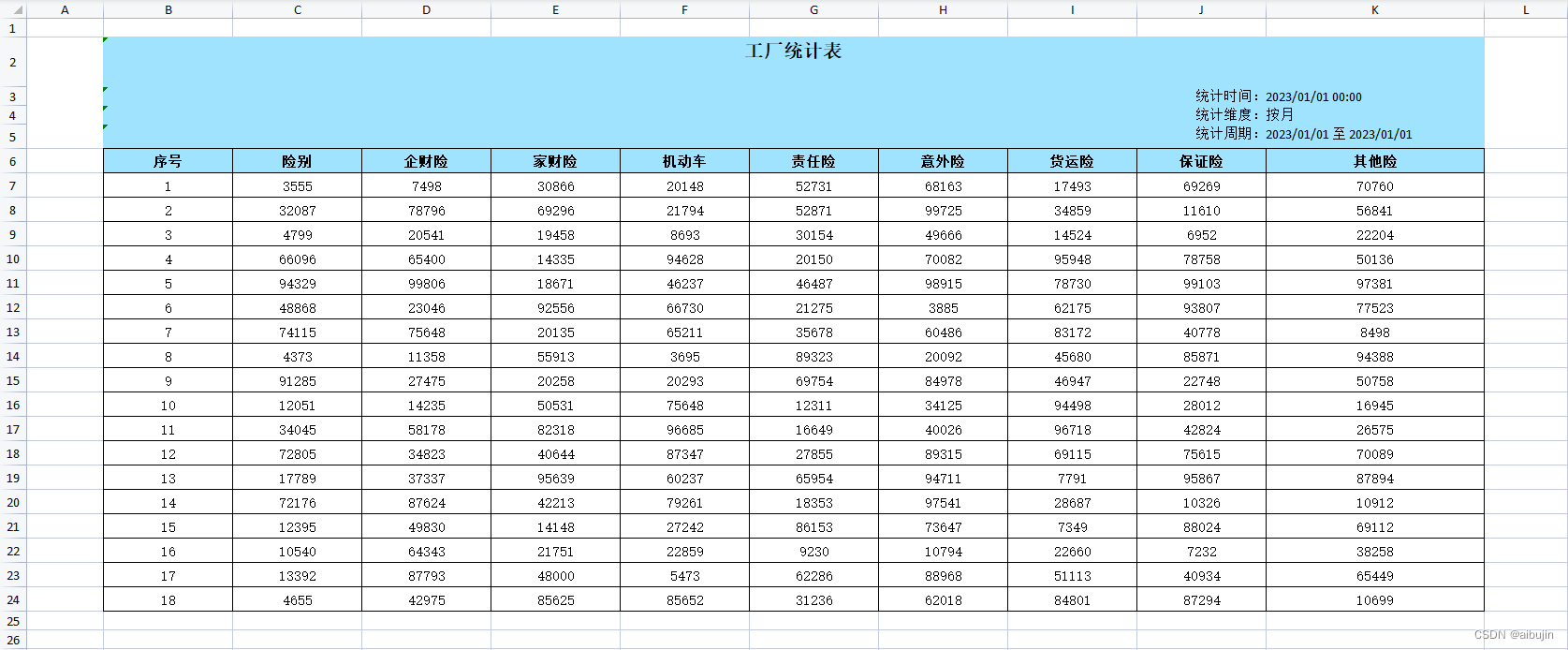
sheetJs / xlsx-js-style 纯前端实现导出 excel 表格及自定义单元格样式
文章目录 一、安装二、创建基础工作表三、设置单元格宽度/高度/隐藏单元格四、分配数字格式五、超链接六、单元格注释七、公式八、合并单元格九、自定义单元格样式十、项目地址 一、安装 xlsx 地址:https://www.npmjs.com/package/xlsxSheetJs 地址:htt…...
Redis 报错 RedisConnectionException: Unable to connect to x.x.x.x:6379
文章目录 Redis报错类型可能解决方案 Redis报错类型 org.springframework.data.redis.connection. spingboot调用redis出错 PoolException: Could not get a resource from the pool; 连接池异常:无法从池中获取资源; nested exception is io.lettuce.core. 嵌套异常 RedisConn…...

Stable Diffusion - 真人照片的高清修复 (StableSR + GFPGAN) 最佳实践
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/132032216 GFPGAN (Generative Facial Prior GAN) 算法,用于实现真实世界的盲脸恢复的算法,利用预训练的面部 GAN…...
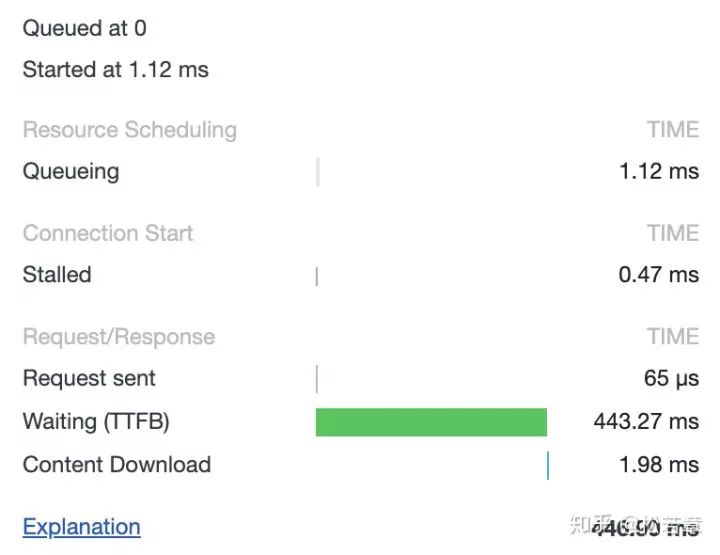
细讲一个 TCP 连接能发多少个 HTTP 请求(一)
一道经典的面试题是从 URL 在浏览器被被输入到页面展现的过程中发生了什么,大多数回答都是说请求响应之后 DOM 怎么被构建,被绘制出来。但是你有没有想过,收到的 HTML 如果包含几十个图片标签,这些图片是以什么方式、什么顺序、建…...

了解 CVSS:通用漏洞评分系统的应用
漏洞威胁管理至关重要,因为网络犯罪是一种持续存在的全球风险。网络犯罪分子愿意利用软件中的任何漏洞来访问网络和设备。对使用该软件的软件开发人员和组织的影响可能很严重。用户必须处理攻击的结果,例如赎金或数据盗窃,并且还可能面临法律…...
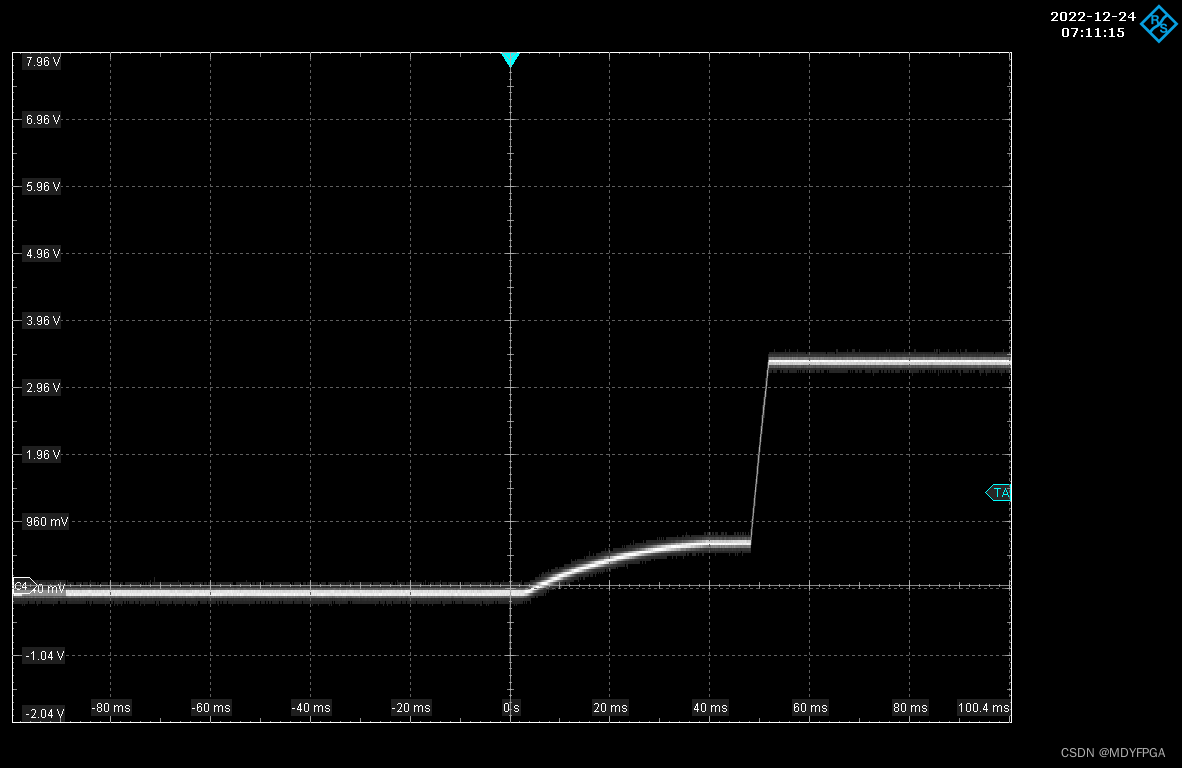
Xilinx FPGA电源设计与注意事项
1 引言 随着半导体和芯片技术的飞速发展,现在的FPGA集成了越来越多的可配置逻辑资源、各种各样的外部总线接口以及丰富的内部RAM资源,使其在国防、医疗、消费电子等领域得到了越来越广泛的应用。当采用FPGA进行设计电路时,大多数FPGA对上电的…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
