【LeetCode 算法】Linked List Cycle II 环形链表 II
Linked List Cycle II 环形链表 II
问题描述:
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
链表中节点的数目范围是 [ 0 , 1 0 4 ] − 1 0 5 < = N o d e . v a l < = 1 0 5 p o s 为 − 1 或者链表中的一个有效索引 链表中节点的数目范围是 [0, 10^4]\\ -10^5 <= Node.val <= 10^5\\ pos 为 -1 或者链表中的一个 有效索引 链表中节点的数目范围是[0,104]−105<=Node.val<=105pos为−1或者链表中的一个有效索引
分析
和昨天的环形链表类似,利用哈希可以在 O ( N ) O(N) O(N)的时间下,找到第一个节点。
另一种就是空间为常数的快慢指针,就是昨天发的那个,它还有个比较学术的名字,Floyd判圈算法(Floyd Cycle Detection Algorithm),它的应用场景很广泛,可以自行Bing,Google。
它的思路比较简单,如果存在环,那么先找到快慢指针在环中的相遇的点 x,然后再让2个指针分别从head,x出发,直到2者相遇,就是环的入口点。
思路很简单,但是大部分人还是不一定能AC。
为什么按照这个思路,可以找到的点一定是入口点?
讨论的前提是有环。
假设入口点是y,那么从 h e a d head head到达y需要 a步,从y到达2指针的相遇点x要走b步,b一定是小于n的,从x继续走c步到达入口y,所以环的大小为 b + c b+c b+c。
f a s t 走的路程 = a + ( k + 1 ) ( b + c ) + b fast 走的路程 = a+ (k+1)(b+c) + b fast走的路程=a+(k+1)(b+c)+b。 a 是无环段,b是环的入口到x的路程,而 ( k + 1 ) ( b + c ) (k+1)(b+c) (k+1)(b+c) 就是跑环的圈数, k > = 0 k>=0 k>=0。
而 s l o w 的路程 = a + b slow的路程 = a+b slow的路程=a+b ,因为fast的速度是slow的2倍,所以路程也是其2倍,即
a + b + ( k + 1 ) ( b + c ) = 2 ∗ ( a + b ) ( k + 1 ) ( b + c ) = a + b k ( b + c ) + c = a a+b +(k+1)(b+c) = 2*(a+b)\\ (k+1)(b+c) = a+b\\ k(b+c)+c = a a+b+(k+1)(b+c)=2∗(a+b)(k+1)(b+c)=a+bk(b+c)+c=a
到这里就会可以得到一个结论,设置2个指针分别从点x和head出发,每次一步,如果相遇就是入口点。
如果你无法理解这个结论.
提示你可以从路程的角度来思考,即一个从x出发的指针,它可能走c,或者是k(b+c)+c,然后恰好与另一个指针在入口相遇。
时间复杂度 O ( N ) 时间复杂度O(N) 时间复杂度O(N)
空间复杂度 O ( 1 ) 空间复杂度O(1) 空间复杂度O(1)
代码
哈希
public boolean hasCycle(ListNode head) {Set<ListNode> set = new HashSet();ListNode p = head;while(p!=null){if(!set.add(p)) return p;p = p.next;}return null;}
时间复杂度 O ( N ) O(N) O(N)
空间复杂度 O ( N ) O(N) O(N)
快慢指针
public ListNode detectCycle(ListNode head) {if(head==null||head.next==null) return null; ListNode vh = new ListNode(-1);vh.next = head;ListNode f = vh, s = vh;while(f!=null&&f.next!=null){ f = f.next.next;s = s.next;if(f==s) break;} if(f==null||f.next==null) return null;ListNode p = vh, q = f;while(p!=q){p = p.next;q = q.next;}return q;}
时间复杂度 O ( N ) O(N) O(N)
空间复杂度 O ( 1 ) O(1) O(1)
Tag
LinkedList
Hash
Two Pointers
相关文章:

【LeetCode 算法】Linked List Cycle II 环形链表 II
文章目录 Linked List Cycle II 环形链表 II问题描述:分析代码哈希快慢指针 Tag Linked List Cycle II 环形链表 II 问题描述: 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链…...

蒸散发与植被总初级生产力估算
目标 熟悉蒸散发ET及其组分(植被蒸腾Ec、土壤蒸发Es、冠层截留Ei)、植被总初级生产力GPP的概念和碳水耦合的基本原理;掌握利用Python与ArcGIS工具进行课程相关的操作;熟练掌握国际上流行的Penman-Monteith模型,并能够…...
uniapp微信小程序底部弹窗自定义组件
基础弹窗效果组件 <template><view><viewclass"tui-actionsheet-class tui-actionsheet":class"[show ? tui-actionsheet-show : ]"><view class"regional-selection">底部弹窗</view></view><!-- 遮罩…...

人工智能的最新进展:2024年将会发生什么?
文章目录 2024年AI最新发展2024年AI具体应用2024年AI的具体预测 ✍创作者:全栈弄潮儿 🏡 个人主页: 全栈弄潮儿的个人主页 🏙️ 个人社区,欢迎你的加入:全栈弄潮儿的个人社区 📙 专栏地址&#…...

使用Golang实现一套流程可配置,适用于广告、推荐系统的业务性框架——组合应用
在《使用Golang实现一套流程可配置,适用于广告、推荐系统的业务性框架——简单应用》中,我们看到了各种组合Handler的组件,如HandlerGroup和Layer。这些组件下面的子模块又是不同组件,比如LayerCenter的子组件是Layer。如果此时我…...
)
DNS入门学习:DNS缓存的原理和作用(中科三方)
在实际业务场景中,DNS解析过程并不总是严格遵循从根域名服务器、顶级域名服务器再到权威域名服务器的一级级查询过程,这只是一个标准状态。为了节省全球查询的时间,同时减轻各级服务器的解析压力,DNS系统中引入了缓存机制。本文中…...
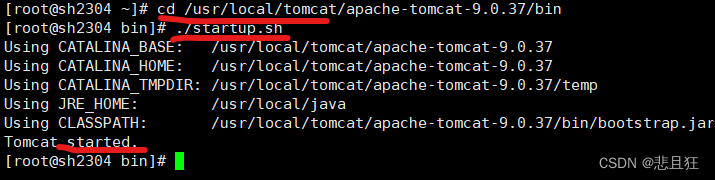
Linux虚拟机安装tomcat(图文详解)
目录 第一章、xshell工具和xftp的使用1.1)xshell下载与安装1.2)xshell连接1.3)xftp下载安装和连接 第二章、安装tomcat1.1)关闭防火墙,传输tomcat压缩包到Linux虚拟机12)启动tomcat 第一章、xshell工具和xf…...
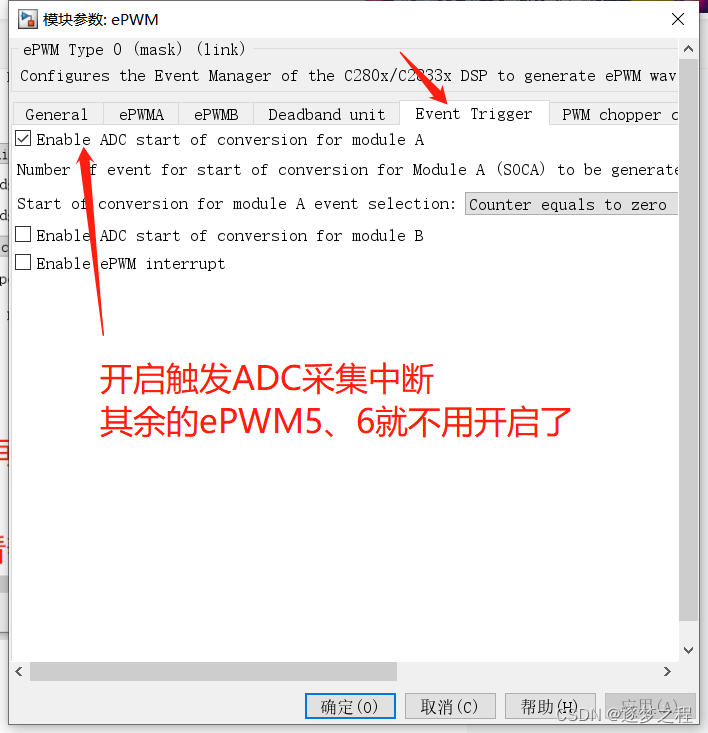
Matlab对TMS320F28335编程--SVPWM配置互补PWM输出
前言 F28335中断 目的:FOC的核心算法及SVPWM输出,SVPWM的载波频率10kHz,SVPWM的每个周期都会触发ADC中断采集相电流,SVPWM为芯片ePWM4、5、6通道,配置死区 1、配置中断SVPWM进ADC中断,查上表知CPU1,PIE1 …...
MySQL数据库——多表操作
文章目录 前言多表关系一对一关系一对多/多对一关系多对多关系 外键约束创建外键约束插入数据删除带有外键约束的表的数据删除外键约束 多表联合查询数据准备交叉连接查询内连接查询外连接查询左外连接查询右外连接查询满外连接查询 子查询子查询关键字ALL 关键字ANY 和 SOME 关…...
Java版本spring cloud + spring boot企业电子招投标系统源代码 tbms
功能模块: 待办消息,招标公告,中标公告,信息发布 描述: 全过程数字化采购管理,打造从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通供应商门户具备内外协同的能力,为…...

css实现,正常情况下div从左到右一次排列,宽度超出时,右侧最后一个div固定住,左侧其他div滚动
需求:正常情况下 宽度超出时: 实现: <templete><div class"jieduanbox"><div v-for"(item, index) in stageList" :key"index" style"display: inline-block">.......</div><div class"rightBtn&q…...

【Linux手动搭建Sftp,创建用户、用户组及删除用户】
SFTP (Secure File Transfer Protocol)是一种安全的文件传输协议,基于SSH协议进行加密传输。在进行文件传输时,SFTP客户端通过SSH协议与服务器进行连接,并且通过使用公钥和/或密码进行身份验证,从而确保传输…...

云上 Index:看「简墨」如何为云原生打造全新索引
拓数派首款数据计算引擎 PieCloudDB Database 是一款全新的云原生虚拟数仓。为了提升用户使用体验,提高查询效率,在实现存算分离的同时,PieCloudDB 设计与打造了全新的存储引擎「简墨」等模块,并针对云场景和分析型场景设计了高效…...
Linux安装cuda和cudnn教程
Linux安装cuda和cudnn教程 文章目录 1.下载cuda和cudnn2. 安装cuda并检验安装是否成功3. 安装cudnn4.验证cuda是否能用代码附件:解压各种格式文件的Linux命令参考文献 卸载之前的cuda 卸载之前的cuda教程 1.下载cuda和cudnn CUDA下载地址:https://dev…...

短视频矩阵源码
一、短视频矩阵源码搭建解析: 目录 一、短视频矩阵源码搭建解析: 二、短视频矩阵源码的开发路径分享: 三、短视频矩阵系统开发应具备哪些能力? 短视频技术开发能力: 开发人员应具备短视频相关技术能力,…...

群狼调研—连锁化妆品品牌门店神秘顾客调查的行家
连锁化妆品品牌门店神秘顾客调查作为群狼调研(湖南专业市场调查)的优势业务之一,公司成立至今已承包包括北京、上海、广州、深圳、长沙在内全国多个城市上百家不同化妆品品牌客户的神秘顾客调查服务,在创新性、行业操守及客户服务等方面赢得了广大客户的…...

C# 回文链表
234 回文链表 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。 示例 1: 输入:head [1,2,2,1] 输出:true 示例 2: 输入&…...

基于freertos的温湿度蓝牙系统
前言:本项目主要是基于freertos的小项目,目的是为了巩固近期学习的知识,功能较简单,可自行扩充。 一、项目基本架构 项目基本功能:通过STM32单片机的freertos操作系统,将温湿度数据显示在oled屏幕上&#…...
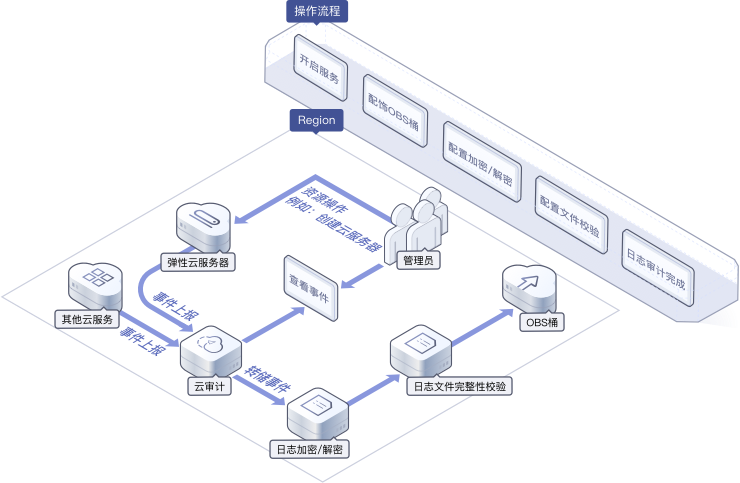
华为云CTS 使用场景
云审计服务 CTS 云审计服务(Cloud Trace Service),帮助您监控并记录华为云账号的活动,包括通过控制台、API、开发者工具对云上产品和服务的访问和使用行为,提供对各种云资源操作记录的收集、存储和查询功能࿰…...
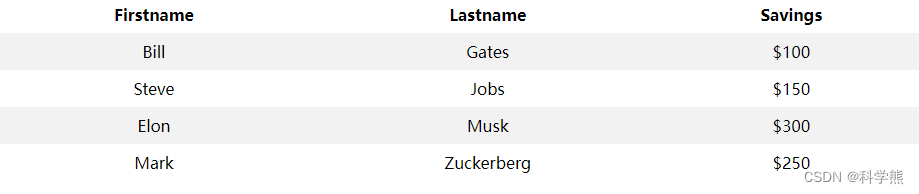
【css】nth-child选择器实现表格的斑马纹效果
nth-child() 选择器可以实现为所有偶数(或奇数)的表格行添加css样式,even:偶数,odd:奇数。 代码: <style> table {border-collapse: collapse;width: 100%; }th, td {text-align: cente…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
