java 框架
目录
- Spring 如何解决 bean 的循环依赖?
- 什么是 AOP?Spring 如何实现的?
- BeanFactory 和 ApplicationContext 有什么区别?
- 介绍一下 Spring bean 的生命周期
- Spring 的隔离级别
- Spring 框架用到了哪些设计模式?并举出典型例子
Spring 如何解决 bean 的循环依赖?
Spring中引入三级缓存是为了解决循环依赖问题。循环依赖是指在创建bean的过程中,存在两个或多个bean相互依赖的情况,形成一个闭环。这样的情况下,如果没有合适的机制来解决循环依赖,会导致bean的创建陷入死循环,最终导致应用程序无法启动或抛出异常。
三级缓存是Spring用来处理循环依赖的特殊机制,其原理如下:
-
第一级缓存(singletonObjects):当Spring创建一个bean时,会先检查是否有其它的实例正在创建中(即是否在第二级缓存
earlySingletonObjects中),如果是,则返回尚未填充属性的实例。如果没有,则创建一个"空壳"(即一个空的bean实例),将其放入第一级缓存singletonObjects中,并继续创建bean的其他依赖。 -
第二级缓存(earlySingletonObjects):当创建bean时,如果发现依赖的其他bean正在创建中(即已经在第一级缓存
singletonObjects中),则将正在创建的bean放入第二级缓存earlySingletonObjects中,作为一个尚未填充属性的实例。 -
第三级缓存(singletonFactories):当创建bean时,如果发现依赖的其他bean还未创建完成(即还没有放入第一级缓存
singletonObjects中),则将创建bean所需的ObjectFactory放入第三级缓存singletonFactories中。
通过这三级缓存的机制,Spring能够在创建bean的过程中解决循环依赖问题。当遇到循环依赖时,Spring会提前暴露正在创建的bean对象,然后继续创建其他依赖的bean,最终再回过头来填充这些“空壳”,从而解决了循环依赖的问题。
需要注意的是,三级缓存主要用于解决单例作用域的bean的循环依赖问题,对于原型作用域的bean,Spring无法解决循环依赖。
什么是 AOP
相关文章:

java 框架
目录 Spring 如何解决 bean 的循环依赖?什么是 AOP?Spring 如何实现的?BeanFactory 和 ApplicationContext 有什么区别?介绍一下 Spring bean 的生命周期Spring 的隔离级别Spring 框架用到了哪些设计模式?并举出典型例子Spring 如何解决 bean 的循环依赖? Spring中引入三…...
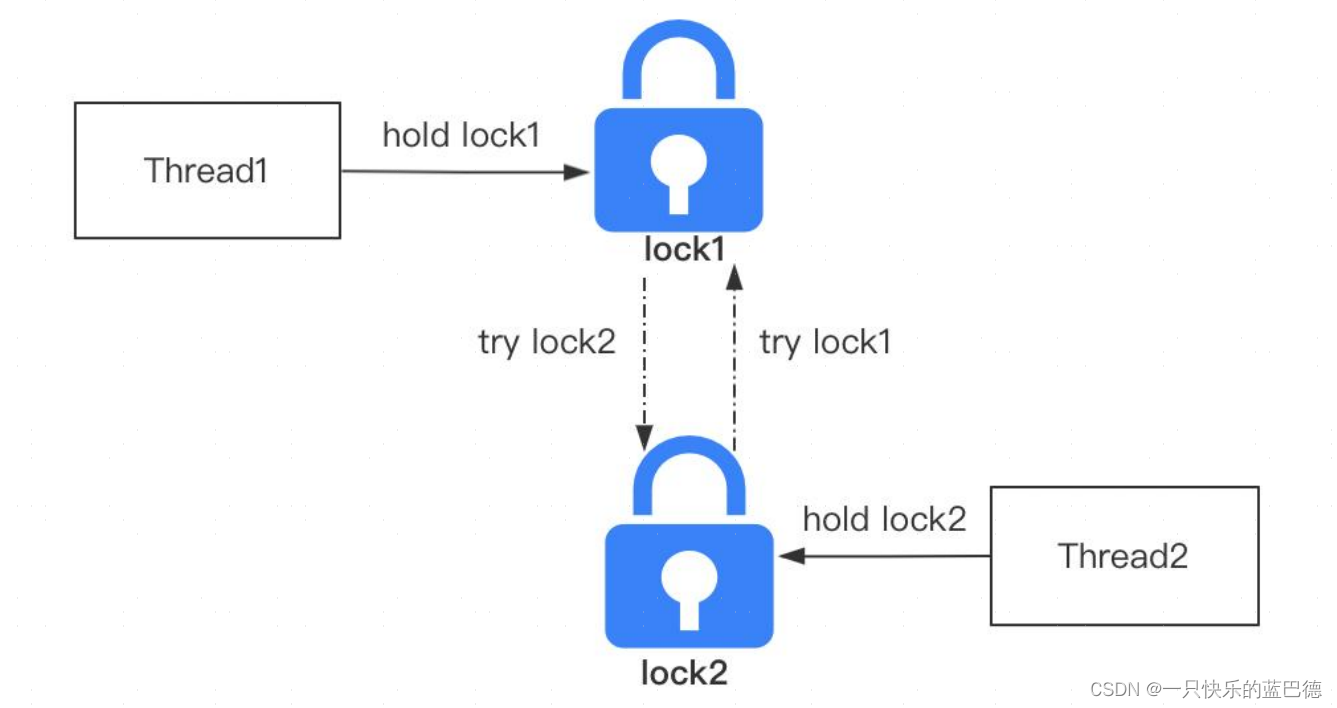
死锁的发生原因和怎么避免
项目场景: 提示:这里简述项目相关背景: 例如:项目场景:示例:通过蓝牙芯片(HC-05)与手机 APP 通信,每隔 5s 传输一批传感器数据(不是很大) 问题描述 死锁,简单来说就是两个或者两个以上的线程在…...
visual studio 生成dll文件以及修改输出dll文件名称操作
目录 visual studio 生成dll文件以及修改dll文件名称一、准备测试代码二、设置导出dll属性三、生成dll文件 .lib .dll .pdb 的简单介绍dll文件使用方式lib文件使用方式1、动态链接 (原理)2、静态链接: visual studio 生成dll文件以及修改dll文…...
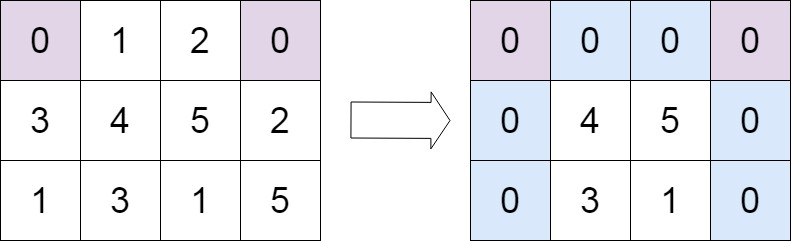
【Leetcode】73.矩阵置零
一、题目 1、题目描述 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例1: 输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例2: 输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1…...
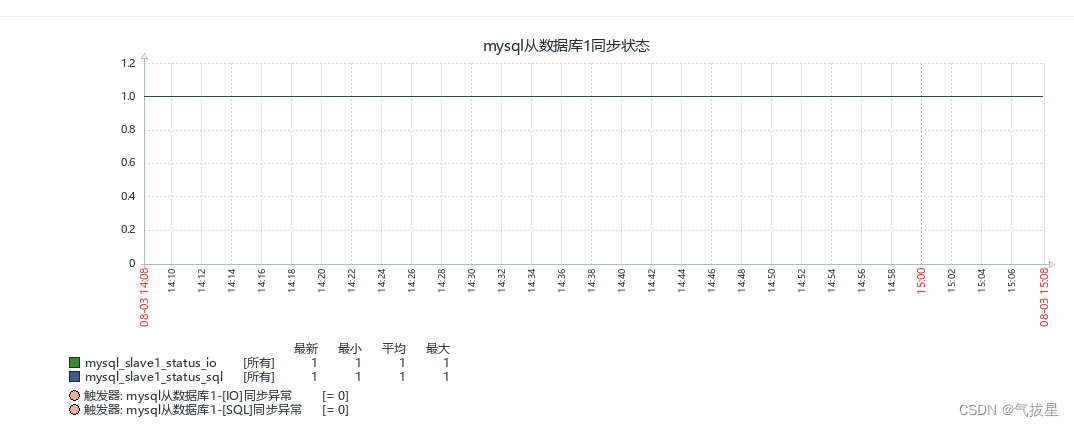
zabbix监控mysql容器主从同步状态并告警钉钉/企业微信
前言:被监控的主机已经安装和配置mysql主从同步,和zabbix-agent插件。 mysql创建主从同步:http://t.csdn.cn/P4MYq centos安装zabbix-agent2:http://t.csdn.cn/fx74i mysql主从同步,主要监控这2个参数指标…...

ARM 常见汇编指令学习 9 - 缓存管理指令 DC 与 IC
文章目录 ARM64 DC 与 IC 指令 上篇文章:ARM 常见汇编指令学习 8 - dsb sy 指令及 dsb 参数介绍 ARM64 DC 与 IC 指令 AArch64指令集中有两条关于缓存维护(cache maintenance)的指令,分别是IC和DC。 IC 是用于指令缓存操作&…...
落地数字化管理,提升企业市场竞争力
数字化企业管理方案是一种利用数字技术和信息系统来提升企业管理效率和运营效果的策略。 潜在的数字化企业管理方案 1、企业资源规划(ERP)系统:建立一个集成的ERP系统来统一管理企业的各项业务流程,包括采购、销售、库存管理、财…...
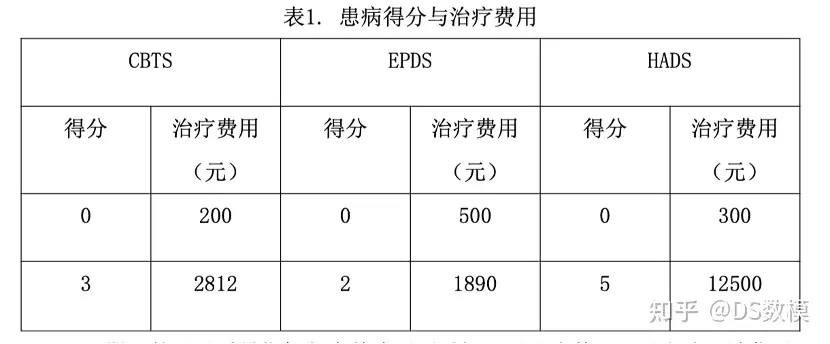
2023华数杯数学建模竞赛C题思路解析
如下为:2023华数杯数学建模竞赛C题 母亲身心健康对婴儿成长的影响 的思路解析 C题 母亲身心健康对婴儿成长的影响 母亲是婴儿生命中最重要的人之一,她不仅为婴儿提供营养物质和身体保护,还为婴儿提供情感支持和安全感。母亲心理健康状态的不…...

Photon之如何解决Photon Server无法在局域网使用的bug
前言 先介绍一下Photon的两个服务器服务: Photon Cloud 是一个完全托管的软件即服务 (SaaS) 解决方案。我们可以完全专注于应用程序客户端,而托管、服务器操作和扩展均由光子官方负责。 Photon Server 是一个本地服务器应用程序,我们可以在本地或指定的计算机上运行和托管。…...
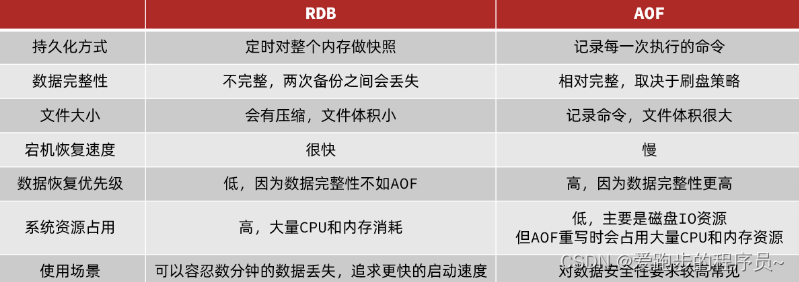
Redis两种持久化方案RDB持久化和AOF持久化
Redis持久化 Redis有两种持久化方案: RDB持久化AOF持久化 1.1.RDB持久化 RDB全称Redis Database Backup file(Redis数据备份文件),也被叫做Redis数据快照。简单来说就是把内存中的所有数据都记录到磁盘中。当Redis实例故障重启…...

银河麒麟v10 vnc环境配置
方法一、启用自带远程桌面 银河麒麟默认已经自带远程桌面,如下图。此时即可用Realvnc Viewer访问该终端,仔细查看后自带的远程桌面是开源组件gnome-remote-desktopGNOME / gnome-remote-desktop GitLabhttps://gitlab.gnome.org/GNOME/gnome-remote-de…...
【动态内存管理助力程序优化与性能飞升】
本章重点 为什么存在动态内存分配 动态内存函数的介绍 malloc free calloc realloc 常见的动态内存错误 几个经典的笔试题 柔性数组 1. 为什么存在动态内存分配 我们已经掌握的内存开辟方式有: int val 20;//在栈空间上开辟四个字节 char arr[10] {0};//在栈…...

电动汽车设计、制造、研发的学科、技术和前沿科技综述
引言:电动汽车作为替代传统燃油汽车的一种先进交通工具,不仅具有环保、低噪音等优势,而且对于能源消耗和气候变化等全球性问题也具有重要意义。本文将综述与电动汽车设计、制造、研发相关的学科、技术和前沿科技,以期对电动汽车领…...
NsPack3.x脱壳手记
发现是NsPack3.x的壳 使用ESP守恒快速脱壳 F9遇到popfd后下面的jmp就是通往OEP了 打开LordPE准备转储映像, 首先调整下ImageSize, 接着dump full 接着不要退出目前的调试, 打开Scylla修复IAT, 把OEP的VA地址输入到OEP处, 接着按照如下图所示步骤 完成后如下, 但NsPack3.x…...

在.net 6.0中 调用远程服务器web服务,Webservices(xxx.asmx) ,RESTful 风格,2种解决方案。
1.使用 Connected Services: 右键单击您的项目,选择 "Add"(添加)-> "Connected Services"(已连接的服务)。 在 "Connected Services" 对话框中,选择 "W…...

深度学习基础01-深度学习简介
什么是深度学习? 深度学习是机器学习的一个分支,是一种基于人工神经网络的学习方法。它是一种模仿人脑神经元之间信息传递和学习的过程的机器学习算法。深度学习的核心思想是通过构建多层神经网络来学习从输入到输出的复杂映射关系,从而实现各…...

Flink DataStream API详解
DataStream API 参考:https://ci.apache.org/projects/flink/flink-docs-release-1.9/dev/datastream_api.html Data Sources Source是程序读取其输入的位置,您可以使用env.addSource(sourceFunction)将Source附加到程序中。Fl…...
函数对图像进行腐蚀操作】)
【如何使用cv::erode()函数对图像进行腐蚀操作】
文章目录 `cv::erode()`函数主要用途`cv::erode()`函数的参数卷积核cv::erode()函数主要用途 cv::erode()函数主要用于进行图像的腐蚀操作。这是一种图像处理技术,通常用于消除图像中的噪声、分离两个连接在一起的物体、或者使物体的边界变得更加明显。 腐蚀操作的基本思想是…...

C++数据结构之BST(二叉搜索树)的实现
目录 BST 的方法摘要查找节点四个引用,都有妙用递归版非递归版 插入节点利用search的返回值更新高度的注意事项插入算法的完整代码 删除节点框架单分支,直接替代双分支,化繁为简代码 code BST 预告:本文是后续实现各种各样平衡二叉…...
QT以管理员身份运行
以下配置后,QT在QT Creator调试时,或者生成的.exe程序,都将会默认以管理员身份运行。 一、MSVC编译器 1、在Pro文件中添加以下代码: QMAKE_LFLAGS /MANIFESTUAC:\"level\requireAdministrator\ uiAccess\false\\" …...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
