2023牛客暑期多校训练营6-A Tree
2023牛客暑期多校训练营6-A Tree
https://ac.nowcoder.com/acm/contest/57360/A
文章目录
- 2023牛客暑期多校训练营6-A Tree
- 题意
- 解题思路
- 代码
题意

解题思路
最大价值和这个数据范围,一眼 d p dp dp。
直接在树上并不好处理,问题是如何有效转化、处理 x , y x,y x,y之间的最短路径上的最大边权值。这里用到了 k r u s k a l 重构树 kruskal重构树 kruskal重构树, k r u s k a l 算法 kruskal算法 kruskal算法是一种贪心地求最小生成树的算法,本题所用算法参照了该算法的思路,将一张无向图的边按边权排序,一次取用,不同的是,我们将每条边转化为带有点权的虚点,任意两点由虚点连接,而原图上的点均为叶子结点,如图:

一条边的两个端点将祖先连在一起,可以用并查集实现。
根据这种树的特殊性质,其虚点的权值自上而下减少,原图上两个点之间的最短路径上的最大权值即为该图上两点最近公共祖先的点权。此时可以进行树形 d p dp dp了!

设 d p x , b dp_{x,b} dpx,b表示以 x x x为根的字数内黑点个数为 b b b的贡献最大值,对于原图上任意边,其贡献值为
( W 1 × B 2 + W 2 × B 1 ) × k (W_1\times B_2+W_2\times B_1)\times k (W1×B2+W2×B1)×k,推理得:
d p x , b = M a x b − s z r ≤ b 1 ≤ m i n ( b , s z l ) ( d p l , b 1 + d p r , b − b 1 + k x × ( b 1 ( 左子树黑点个数 ) × ( s z r − b + b 1 ) ( 右子树白点个数 ) + ( s z l − b 1 ) ( 左子树白点个数 ) × ( b − b 1 ) ( 右子树黑点个数 ) ) ) dp_{x,b}=Max_{b-sz_r\le b_1\le min(b,sz_l)}(dp_{l,b_1}+dp_{r,b-b_1}+\\ k_x\times(b_1(左子树黑点个数)\times(sz_r-b+b_1)(右子树白点个数)+\\ (sz_l-b_1)(左子树白点个数)\times(b-b_1)(右子树黑点个数))) dpx,b=Maxb−szr≤b1≤min(b,szl)(dpl,b1+dpr,b−b1+kx×(b1(左子树黑点个数)×(szr−b+b1)(右子树白点个数)+(szl−b1)(左子树白点个数)×(b−b1)(右子树黑点个数)))
对于叶子结点 l e a f leaf leaf:
d p l e a f , a [ l e a f ] ⊕ 1 = − c o s t l e a f d p l e a f , a [ l e a f ] = 0 dp_{leaf,a[leaf]\oplus 1}=-cost_{leaf}\\ dp_{leaf,a[leaf]}=0 dpleaf,a[leaf]⊕1=−costleafdpleaf,a[leaf]=0
注意内存与结果大小, d p dp dp数组可以用 v e c t o r < l o n g l o n g > vector<long long> vector<longlong>。
代码
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int N=6005;
int n,a[N],c[N],f[N],m,sz[N],b[N];
pair<int,int>e[N];
struct node{int u,v,w;
}p[N];
vector<ll> dp[N];
bool cmp(node a,node b){return a.w<b.w;
}
int sf(int x){if(f[x]==x)return x;return f[x]=sf(f[x]);
}
void dfs(int u){if(u<=n){dp[u][a[u]^1]=-c[u];dp[u][a[u]]=0;sz[u]=1;return;}int l=e[u].first,r=e[u].second;dfs(l),dfs(r);sz[u]=sz[l]+sz[r];dp[u]=vector<ll>(sz[u]+1,-0x3f3f3f3f3f3f);if(sz[l]>sz[r])swap(l,r);for(int x=0;x<=sz[u];x++)for(int i=max(0,x-sz[r]);i<=min(sz[l],x);i++){dp[u][x]=max(dp[u][x],dp[l][i]+dp[r][x-i]+b[u]*(i*(sz[r]-x+i)+(sz[l]-i)*(x-i)));}
}
int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i],dp[i].resize(2);for(int i=1;i<=2*n;i++)f[i]=i;for(int i=1;i<=n;i++)cin>>c[i];for(int i=1;i<n;i++){int u,v,w;cin>>u>>v>>w;p[i].u=u,p[i].v=v,p[i].w=w;}sort(p+1,p+n,cmp);m=n;for(int i=1;i<n;i++){int u=p[i].u,v=p[i].v,w=p[i].w;if(sf(u)==sf(v))continue;++m;b[m]=w;e[m].first=sf(u),e[m].second=sf(v);f[sf(u)]=f[sf(v)]=m;}dfs(sf(1));ll ans=0;for(int i=0;i<=n;i++){ans=max(ans,dp[sf(1)][i]);}cout<<ans;
}
相关文章:

2023牛客暑期多校训练营6-A Tree
2023牛客暑期多校训练营6-A Tree https://ac.nowcoder.com/acm/contest/57360/A 文章目录 2023牛客暑期多校训练营6-A Tree题意解题思路代码 题意 解题思路 最大价值和这个数据范围,一眼 d p dp dp。 直接在树上并不好处理,问题是如何有效转化、处理…...

Vc - Qt - QPainter::SmoothPixmapTransform及QPainter::Antialiasing
QPainter::SmoothPixmapTransform是一个标志,用于指定绘制操作中的平滑像素变换行为。当使用QPainter绘制一幅图像时,设置SmoothPixmapTransform标志可以使图像变换过程更加平滑,减少锯齿状边缘的出现。此标志通常用于绘制缩放后图像的情况。…...

【练习】条件变量:创建三个线程 id号为ABC,三个线程循环打印自己的ID号,运行顺序为 ABCABC
题目: 创建三个线程 id号为ABC,三个线程循环打印自己的ID号,运行顺序为 ABCABC......要求使用条件变量 #include <stdio.h> #include <pthread.h> #include <unistd.h>//创建互斥锁 pthread_mutex_t mutex PTHREAD_MUTE…...
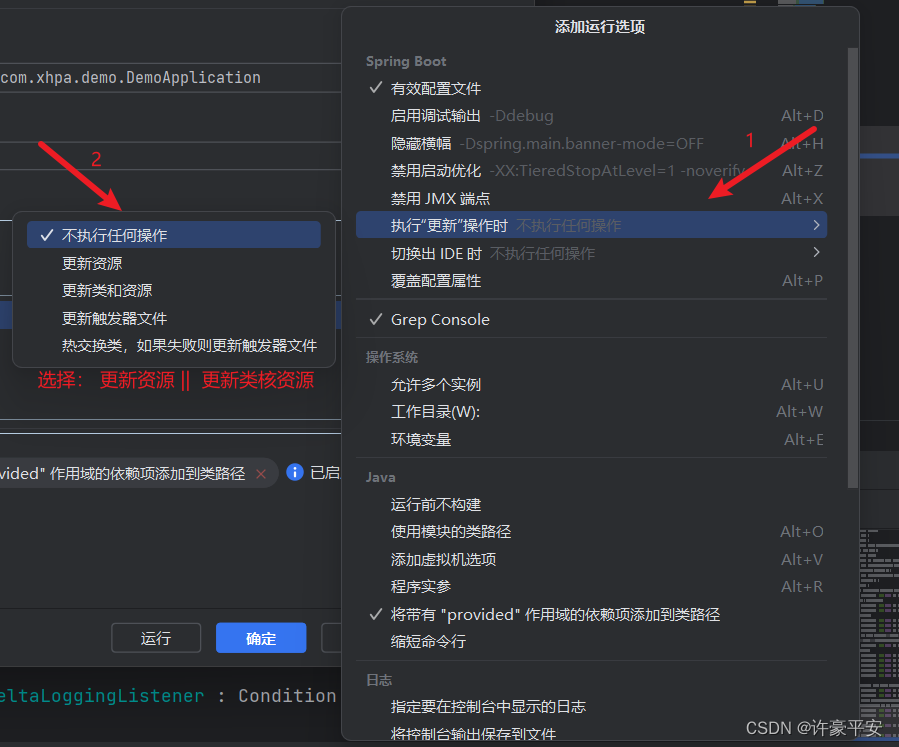
SpringBoot项目修改中静态资源,只需刷新页面无需重启项目(附赠—热加载)
初衷 💢初衷💢 因为一遍遍修改并重启项目觉得很麻烦,所以刚开始就自己给项目配置了热加载,但奈何代码更新还是慢,还不如我重启一遍项目的速度,所以放弃了自己上网找到的热加载配置。直到我debugger前端代码…...

clear_data_code_2d_model
dev update off () dev close window () ImageFiles:-./二维条码/read_image(Image,ImageFiles 十二维条码原图.png)dev_open_window_fit_image(Image,0,0,-,-1,WindowHandle)set_display_font (WindowHan…...

“深入剖析JVM:揭秘Java虚拟机的工作原理“
标题:深入剖析JVM:揭秘Java虚拟机的工作原理 摘要:本文将深入探讨Java虚拟机(JVM)的工作原理,包括JVM的架构、内存管理、垃圾回收、即时编译等关键技术。通过对JVM的剖析,我们可以更好地理解Ja…...

elementui表格table中实现内容的换行
问题 elementui 中的 table 行内的内容不能进行换行。 解决方法 思路: 利用 作用域插槽 结合 v-html,通过作用域插槽传递内容到表格行内,再通过 v-html 进行内容的替换。 代码: <el-table:data"tableData"stri…...

java 框架
目录 Spring 如何解决 bean 的循环依赖?什么是 AOP?Spring 如何实现的?BeanFactory 和 ApplicationContext 有什么区别?介绍一下 Spring bean 的生命周期Spring 的隔离级别Spring 框架用到了哪些设计模式?并举出典型例子Spring 如何解决 bean 的循环依赖? Spring中引入三…...
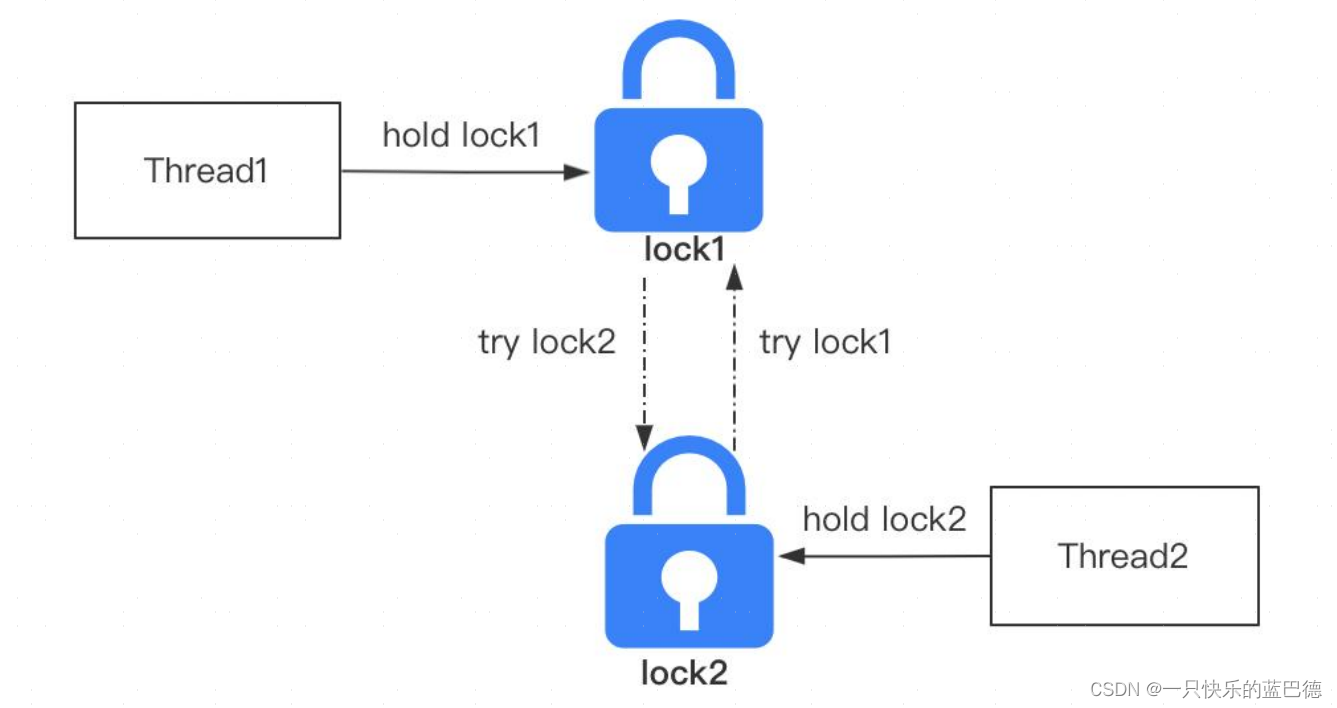
死锁的发生原因和怎么避免
项目场景: 提示:这里简述项目相关背景: 例如:项目场景:示例:通过蓝牙芯片(HC-05)与手机 APP 通信,每隔 5s 传输一批传感器数据(不是很大) 问题描述 死锁,简单来说就是两个或者两个以上的线程在…...
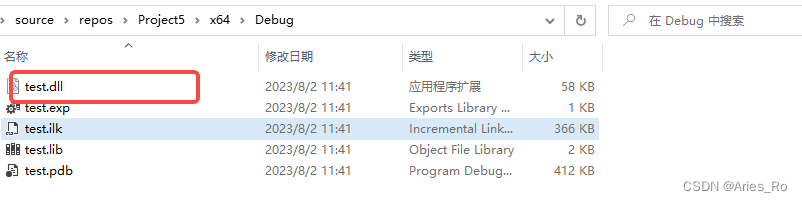
visual studio 生成dll文件以及修改输出dll文件名称操作
目录 visual studio 生成dll文件以及修改dll文件名称一、准备测试代码二、设置导出dll属性三、生成dll文件 .lib .dll .pdb 的简单介绍dll文件使用方式lib文件使用方式1、动态链接 (原理)2、静态链接: visual studio 生成dll文件以及修改dll文…...
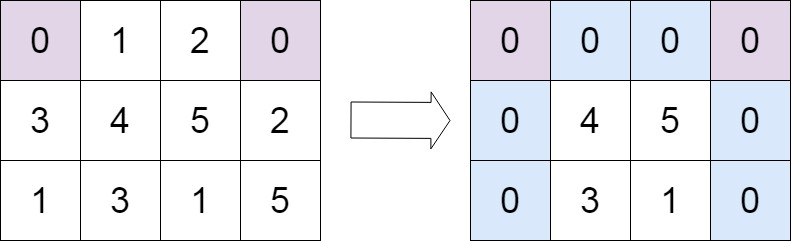
【Leetcode】73.矩阵置零
一、题目 1、题目描述 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例1: 输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例2: 输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1…...
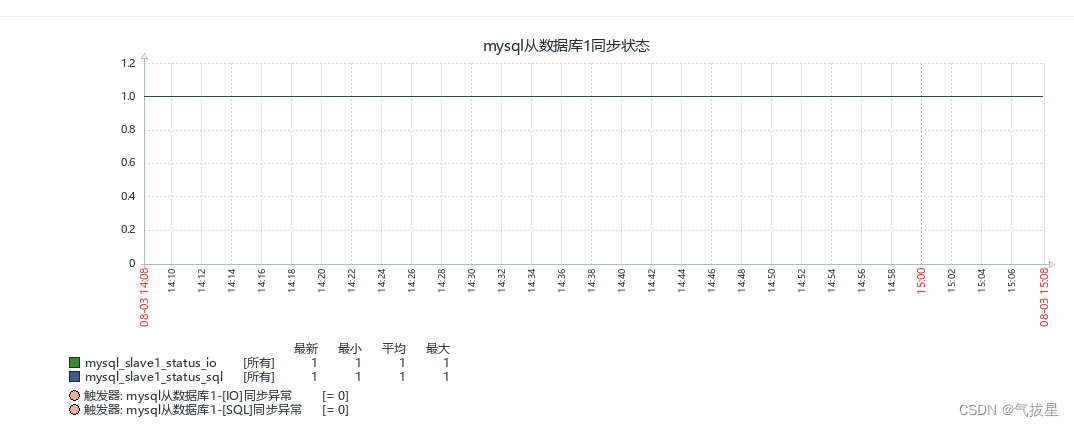
zabbix监控mysql容器主从同步状态并告警钉钉/企业微信
前言:被监控的主机已经安装和配置mysql主从同步,和zabbix-agent插件。 mysql创建主从同步:http://t.csdn.cn/P4MYq centos安装zabbix-agent2:http://t.csdn.cn/fx74i mysql主从同步,主要监控这2个参数指标…...

ARM 常见汇编指令学习 9 - 缓存管理指令 DC 与 IC
文章目录 ARM64 DC 与 IC 指令 上篇文章:ARM 常见汇编指令学习 8 - dsb sy 指令及 dsb 参数介绍 ARM64 DC 与 IC 指令 AArch64指令集中有两条关于缓存维护(cache maintenance)的指令,分别是IC和DC。 IC 是用于指令缓存操作&…...
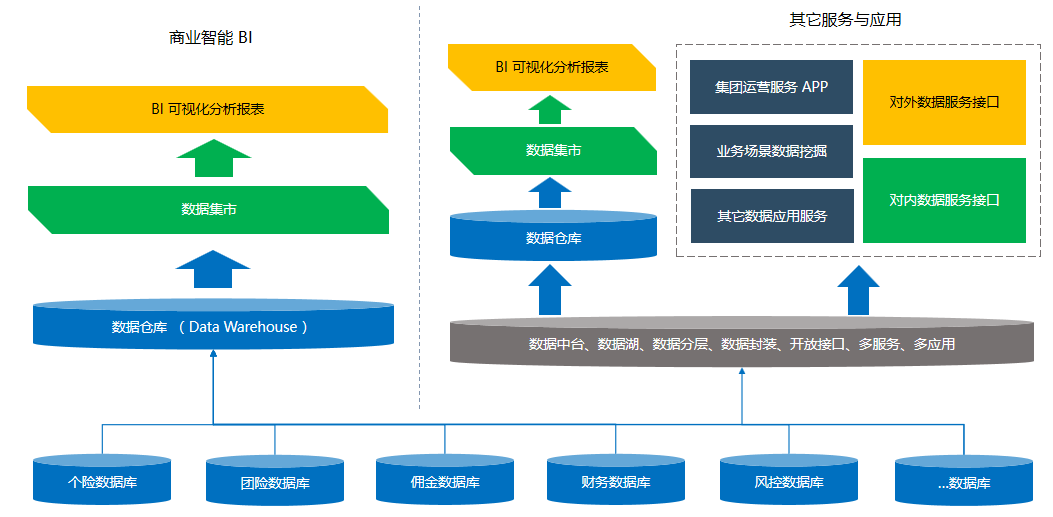
落地数字化管理,提升企业市场竞争力
数字化企业管理方案是一种利用数字技术和信息系统来提升企业管理效率和运营效果的策略。 潜在的数字化企业管理方案 1、企业资源规划(ERP)系统:建立一个集成的ERP系统来统一管理企业的各项业务流程,包括采购、销售、库存管理、财…...
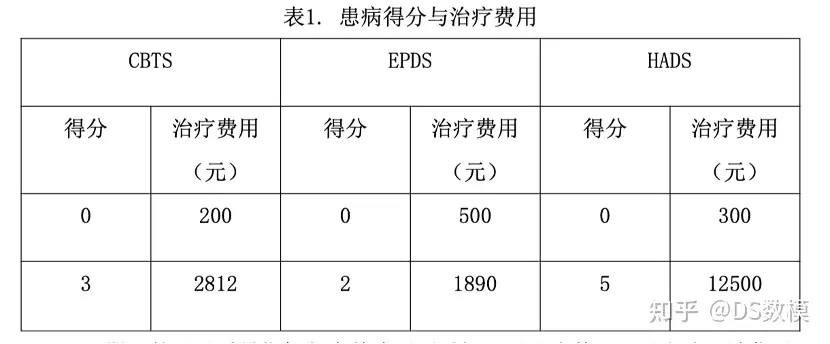
2023华数杯数学建模竞赛C题思路解析
如下为:2023华数杯数学建模竞赛C题 母亲身心健康对婴儿成长的影响 的思路解析 C题 母亲身心健康对婴儿成长的影响 母亲是婴儿生命中最重要的人之一,她不仅为婴儿提供营养物质和身体保护,还为婴儿提供情感支持和安全感。母亲心理健康状态的不…...

Photon之如何解决Photon Server无法在局域网使用的bug
前言 先介绍一下Photon的两个服务器服务: Photon Cloud 是一个完全托管的软件即服务 (SaaS) 解决方案。我们可以完全专注于应用程序客户端,而托管、服务器操作和扩展均由光子官方负责。 Photon Server 是一个本地服务器应用程序,我们可以在本地或指定的计算机上运行和托管。…...
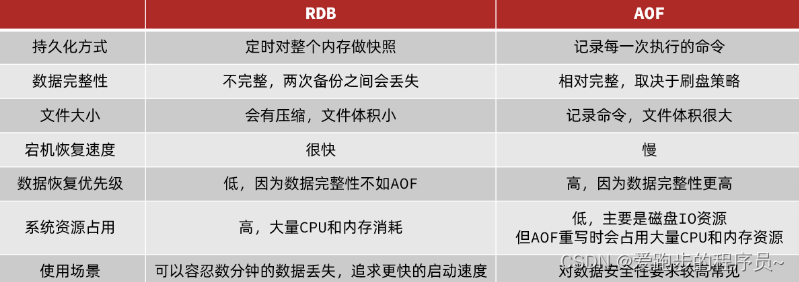
Redis两种持久化方案RDB持久化和AOF持久化
Redis持久化 Redis有两种持久化方案: RDB持久化AOF持久化 1.1.RDB持久化 RDB全称Redis Database Backup file(Redis数据备份文件),也被叫做Redis数据快照。简单来说就是把内存中的所有数据都记录到磁盘中。当Redis实例故障重启…...

银河麒麟v10 vnc环境配置
方法一、启用自带远程桌面 银河麒麟默认已经自带远程桌面,如下图。此时即可用Realvnc Viewer访问该终端,仔细查看后自带的远程桌面是开源组件gnome-remote-desktopGNOME / gnome-remote-desktop GitLabhttps://gitlab.gnome.org/GNOME/gnome-remote-de…...
【动态内存管理助力程序优化与性能飞升】
本章重点 为什么存在动态内存分配 动态内存函数的介绍 malloc free calloc realloc 常见的动态内存错误 几个经典的笔试题 柔性数组 1. 为什么存在动态内存分配 我们已经掌握的内存开辟方式有: int val 20;//在栈空间上开辟四个字节 char arr[10] {0};//在栈…...

电动汽车设计、制造、研发的学科、技术和前沿科技综述
引言:电动汽车作为替代传统燃油汽车的一种先进交通工具,不仅具有环保、低噪音等优势,而且对于能源消耗和气候变化等全球性问题也具有重要意义。本文将综述与电动汽车设计、制造、研发相关的学科、技术和前沿科技,以期对电动汽车领…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...
