第三章 图论 No.2单源最短路之虚拟源点，状压最短路与最短路次短路条数

dp是特殊的最短路，是无环图（拓扑图）上的最短路问题

1137. 选择最佳线路

1137. 选择最佳线路 - AcWing题库

// 反向建图就行
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;typedef pair<int, int> PII;
const int N = 1e3 + 10, M = 2e4 + 10;
int h[N], e[M], ne[M], w[M], idx;
int n, m, s;
int a[N];
int dis[N]; bool st[N];void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void dijkstra()
{priority_queue<PII, vector<PII>, greater<PII>> q;memset(dis, 0x3f, sizeof(dis));memset(st, 0, sizeof(st));dis[s] = 0;q.push({ dis[s], s });while (q.size()){auto t = q.top(); q.pop();int x = t.second, d = t.first;if (st[x]) continue;st[x] = true;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (dis[y] > d + w[i]) {dis[y] = d + w[i];q.push({ dis[y], y });}}}
}int main()
{while (~scanf("%d%d%d", &n, &m, &s)){idx = 0;memset(h, -1, sizeof(h));int x, y, d;while ( m -- ){scanf("%d%d%d", &x, &y, &d);add(y, x, d);}int wn;scanf("%d", &wn);for (int i = 1; i <= wn; ++ i ) scanf("%d", &a[i]);dijkstra();int res = 0x3f3f3f3f;for (int i = 1; i <= wn; ++ i ) res = min(res, dis[a[i]]);if (res == 0x3f3f3f3f) puts("-1");else printf("%d\n", res);}return 0;
}

对于每组测试数据，该重置的数据要重置，我没有重置idx，导致TLE

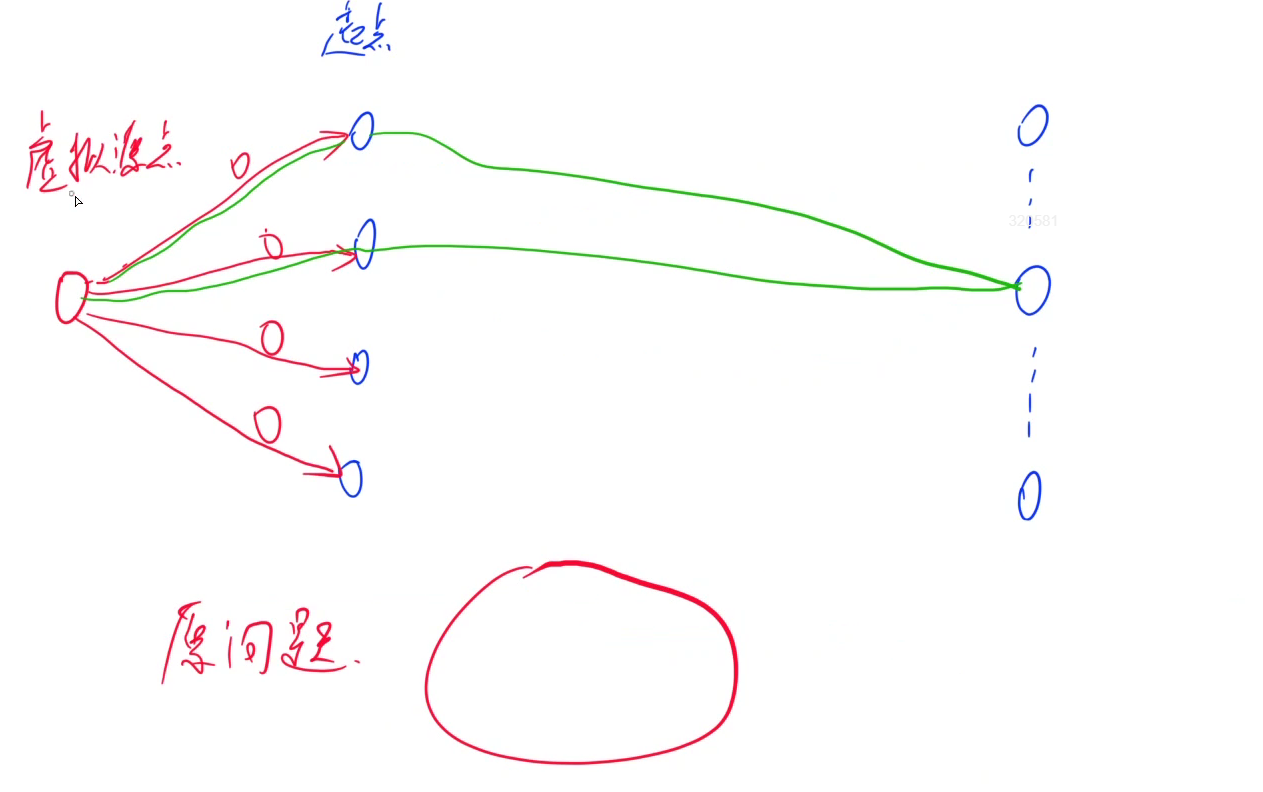
处理反向建图，还有一种扩展做法：虚拟源点

设置虚拟源点，与每个起点之间连接边权为0的边
原问题：从多个源点出发，到达终点的最短路径
先问题：从虚拟源点出发，到达终点的最短路径
两者的最短路径一一对应，并且路径和相同

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;typedef pair<int, int> PII;
const int N = 1e3 + 10, M = 3e4 + 10;
int h[N], e[M], ne[M], w[M], idx;
int n, m, s;
int a[N];
int dis[N]; bool st[N];void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void dijkstra()
{priority_queue<PII, vector<PII>, greater<PII>> q;memset(dis, 0x3f, sizeof(dis));memset(st, 0, sizeof(st));dis[0] = 0;q.push({ dis[0], 0 });while (q.size()){auto t = q.top(); q.pop();int x = t.second, d = t.first;if (st[x]) continue;st[x] = true;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (dis[y] > d + w[i]) {dis[y] = d + w[i];q.push({ dis[y], y });}}}
}int main()
{while (~scanf("%d%d%d", &n, &m, &s)){idx = 0;memset(h, -1, sizeof(h));int x, y, d;while ( m -- ){scanf("%d%d%d", &x, &y, &d);add(x, y, d);}int wn;scanf("%d", &wn);for (int i = 1; i <= wn; ++ i ) {scanf("%d", &a[i]);add(0, a[i], 0);  // 设置虚拟源点}dijkstra();if (dis[s] == 0x3f3f3f3f) puts("-1");else printf("%d\n", dis[s]);}return 0;
}

debug：将虚拟源点与起点之间建立边，要注意M的大小是否足够，又是M开小了…

---

1131. 拯救大兵瑞恩

1131. 拯救大兵瑞恩 - AcWing题库

从集合的角度分析
状态表示：
集合：起点为左上角，终点为图中任意一点的所有路径，用$f(x,y)$表示终点为$[x,y]$的路径
属性：最小时间（路径和）
所以$f(x,y)$表示终点为$[x,y]$的最小路径和
但是图中存在无法通过的墙以及需要钥匙打开的门，所以用两个维度表示路径将无法更新集合
考虑增加一个维度$state$，状态压缩，表示拥有的钥匙状态
即$f(x,y,state)$表示拥有钥匙的状态为$state$时，递达$[x,y]$的最短路

状态计算：
如何划分$f(x,y,state)$？一般的dp问题是从后往前考虑，图论中的集合分析一般从前往后考虑
即$f(x,y,state)$能推导出哪些集合？
若$[x,y]$有钥匙，可以捡起这些钥匙，假设钥匙的状态为key，那么状态推导就是$f(x,y,state)->f(x,y,state|key)$
若$[x,y]$无钥匙，那么可以向相邻的位置走，$f(x,y,state)->f(nx,ny,state)$，此时的最短距离要+1
由于这个问题中存在环路，所以无法用dp更新集合，只能用最短路算法更新集合

这题比较麻烦的是：建边，相邻两个位置若没有墙，那么可以建立一条权值为1的边
如何表示两个二维坐标之间有边？这里涉及到二维坐标到一维的转换，然后用邻接表存储图
若两个位置之间存在门，用边权表示门的种类，但是实际的边权为1
若两个位置之间既不存在门，也不存在墙，那么创建一条权值为0的边，但时间的边权为1。所以$w[i]$为非0表示这个边上有道门，为0表示可以直接通过
对于墙的情况，直接忽略，不建立边（表示不连通）即可
用set存储已经建立的边，防止重复建边

#include <iostream>
#include <cstring>
#include <deque>
#include <set>
using namespace std;typedef pair<int, int> PII;
const int N = 11, P = 1 << N;
const int M = 400;
int h[N * N], e[M], ne[M], w[M], idx;
int g[N][N]; // 二维到一维的转换
int key[N * N]; // 每个坐标的钥匙状态
int dis[N * N][P]; bool st[N * N][P];
set<PII> s;int n, m, p, k;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void build()
{int dx[4] = { 0, 1, 0, -1}, dy[4] = { 1, 0, -1, 0 };for (int x = 1; x <= n; ++ x )for (int y = 1; y <= m; ++ y )for (int i = 0; i < 4; ++ i ){int nx = x + dx[i], ny = y + dy[i];if (nx > 0 && nx <= n && ny > 0 && ny <= m){int a = g[x][y], b = g[nx][ny];if (!s.count({a, b})) add(a, b, 0);}}
}int bfs()
{memset(dis, 0x3f, sizeof(dis));deque<PII> q;dis[1][0] = 0;q.push_back({1, 0});while (q.size()){auto t = q.front(); q.pop_front();int x = t.first, state = t.second;if (st[x][state]) continue;st[x][state] = true;if (x == n * m) return dis[n * m][state];if (key[x]){int nstate = state | key[x];if (dis[x][nstate] > dis[x][state]){dis[x][nstate] = dis[x][state];q.push_front({x, nstate});}}for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (w[i] && !((state >> w[i]) & 1)) continue;if (dis[y][state] > dis[x][state] + 1){dis[y][state] = dis[x][state] + 1;q.push_back({y, state});}}}   return -1;
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d%d%d", &n, &m, &p, &k);int cnt = 1;for (int i = 1; i <= n; ++ i )for (int j = 1; j <= m; ++ j ) g[i][j] = cnt ++ ;int x1, y1, x2, y2, x, y, d;while ( k -- ){scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &d);x = g[x1][y1], y = g[x2][y2];s.insert({x, y}), s.insert({y, x});if (d) add(x, y, d), add(y, x, d);}build(); // 建立除了门和墙的边int l;scanf("%d", &l);while ( l -- ){scanf("%d%d%d", &x, &y, &d);key[g[x][y]] |= 1 << d;}printf("%d\n", bfs());return 0;
}

debug：int x = t.first, state = t.second写成int x = t.secnd, state = t.first
只能说是dijkstra写多了

---

1134. 最短路计数

1134. 最短路计数 - AcWing题库

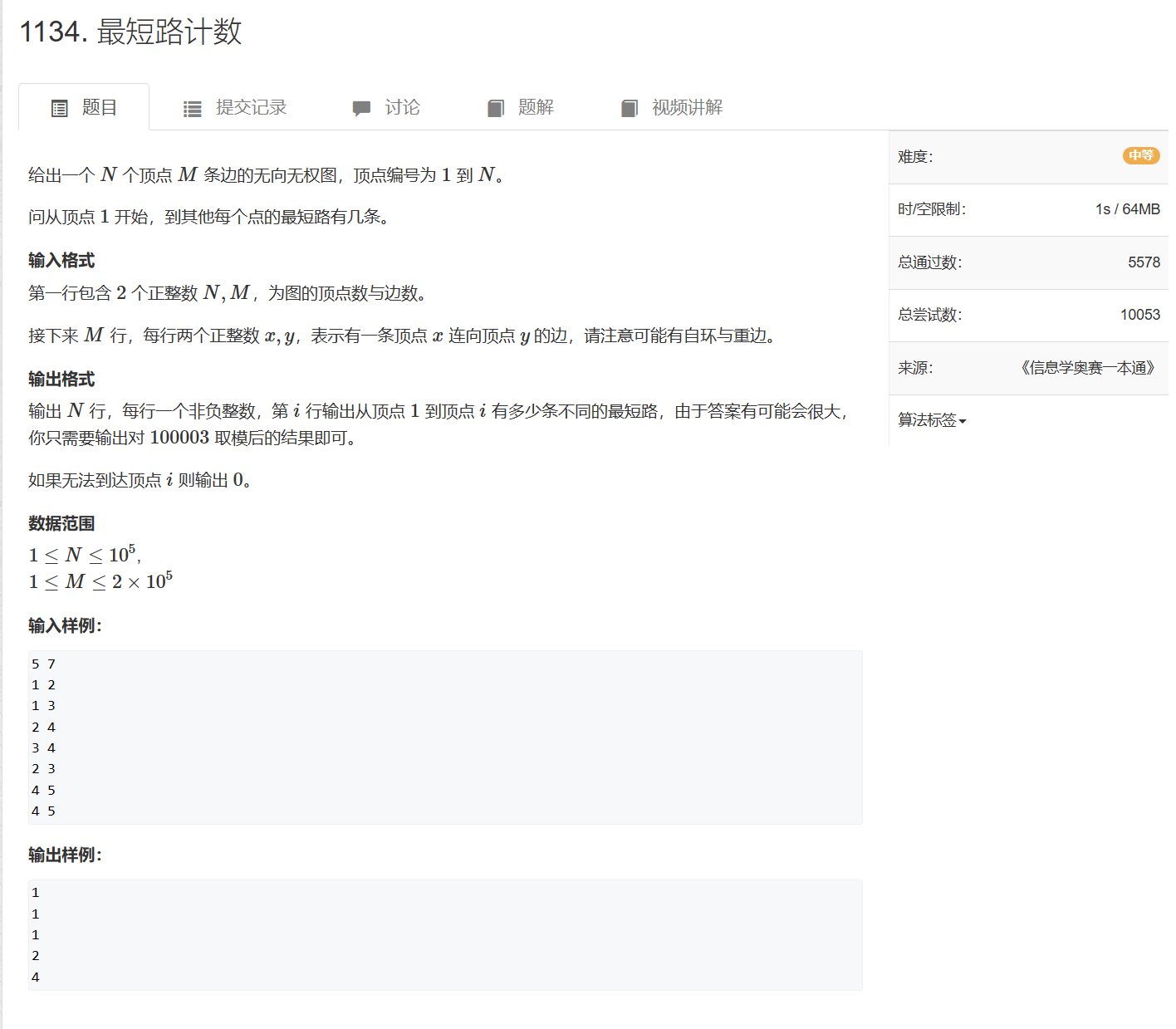
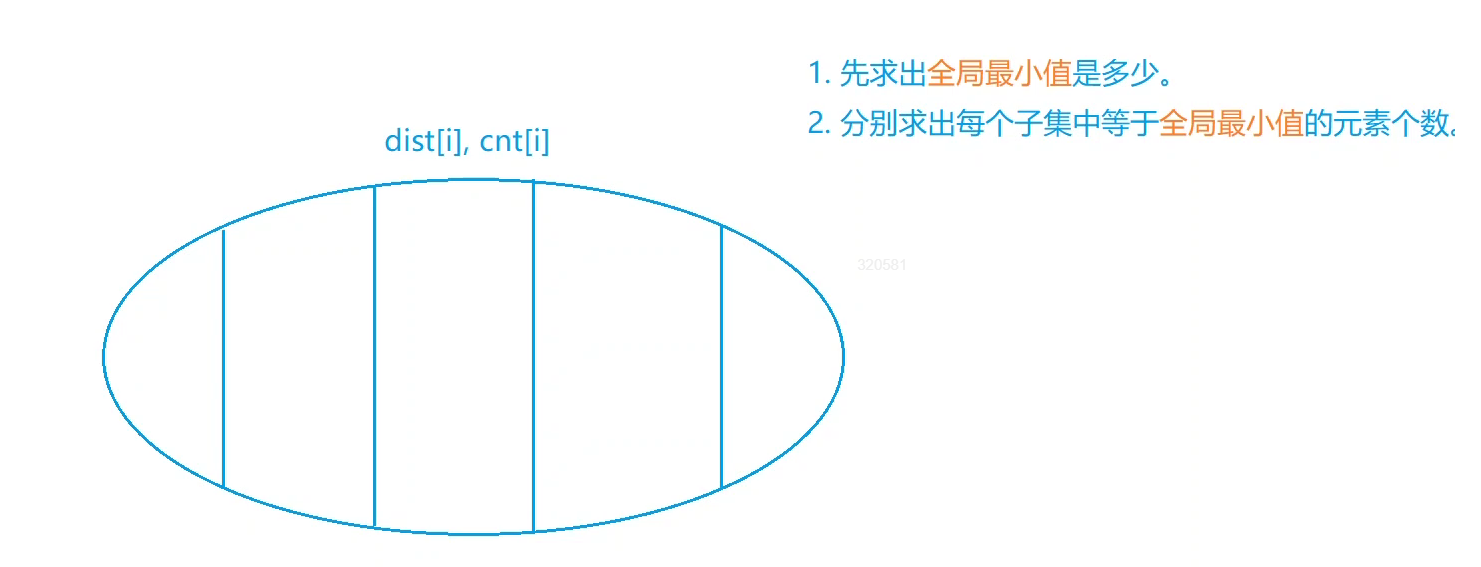
从集合的角度考虑，$f(i)$表示图中第i个点的最短路条数，假设与i相连的点由k个，那么$f(i)=f(s_1)+f(s_2)+...+f(s_k)$，第i个点的最短路条数由与之直接相连的点的最短路条数累加而成
那么要求解$f(i)$，就要先算出它的子集，但是图论问题可能存在环，无法确定$f(i)$是否会影响它的子集。所以只能在拓扑图中才能这样更新集合，考虑最短路算法的更新是否具有拓扑序

三种求最短路的方法：1.BFS 2.Dijkstra 3.Bellman-ford
探讨它们求解最短路时，是否具有拓扑序？
对于BFS，由于每个点只会入队一次且只会出队一次，说明BFS的更新天然地具有拓扑序，因为出队的点不会被后续入队的点影响
对于Dijkstra，由于每个点会入队多次，但只会出队一次，也说明了Dijkstra的更新天然地具有拓扑序
对于spfa，由于它是暴力算法的优化，每个点都会入队与出队多次，所以spfa的更新不具有拓扑序，已经出队（更新完成）的点可能影响被后续入队的点影响
即bfs和dijkstra的更新是一颗最短路树，而spfa的更新不是一颗最短路树

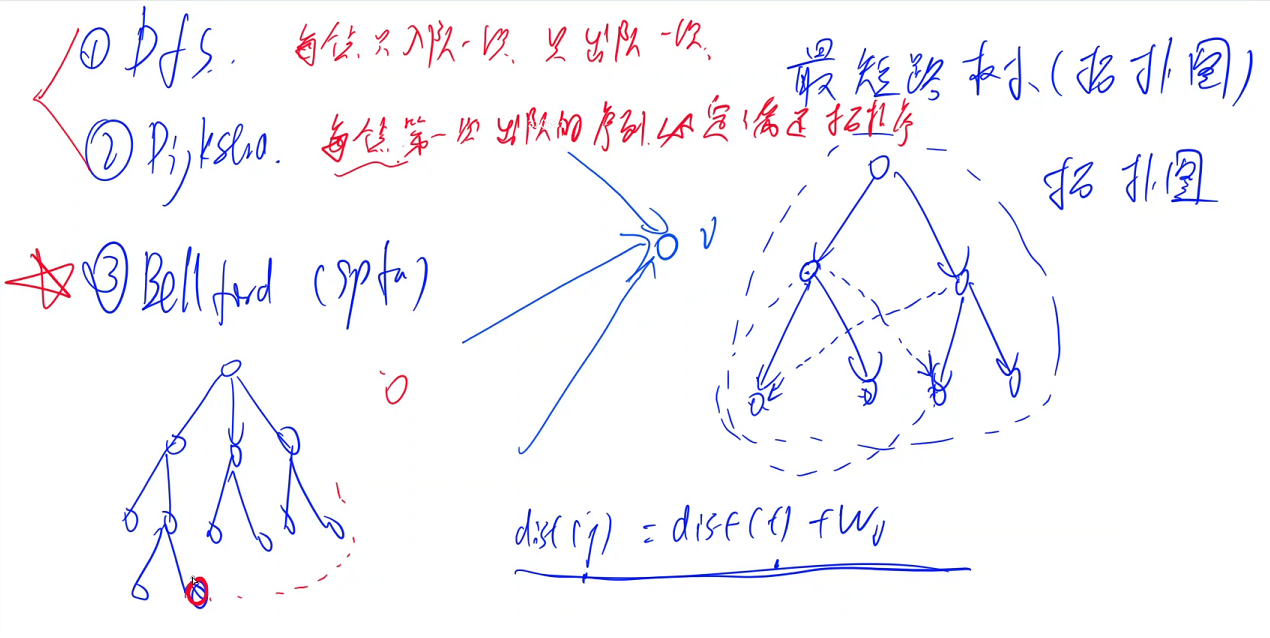
统计最短路条数时，可以遍历最短路树
若统计i节点的最短路条数，只需要累乘父节点的数量即可
而spfa的更新不具有拓扑序，即不存在最短路树，要是图中存在负权边，无法使用天然具有拓扑序的bfs和dijkstra时，只能先用spfa求出最短路，维护出最短路树，再求最短路条数

一般情况下，图中不能存在权值为0的点，否则无法建立出最短路树，因为达到某一个点的最短路不能确定

这题直接用bfs更新最短路，在更新过程中完成最短路条数的统计：用x更新y时，dis[y] > dis[x] + 1时，y的最短路数量等于x的最短路数量
若dis[y] == dix[x] + 1，y的最短路条数等于两者的数量累加

#include <iostream>
#include <cstring>
using namespace std;const int N = 1e5 + 10, M = 4e5 + 10, mod = 100003;
int h[N], e[M], ne[M], idx;
int dis[N], q[N], hh, tt = -1;
int cnt[N];
int n, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void bfs()
{memset(dis, 0x3f, sizeof(dis));q[++ tt ] = 1;dis[1] = 0, cnt[1] = 1;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (dis[y] > dis[x] + 1){dis[y] = dis[x] + 1;q[++ tt ] = y;cnt[y] = cnt[x];}else if(dis[y] == dis[x] + 1) cnt[y] = (cnt[y] + cnt[x]) % mod;}}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);int x, y;while ( m -- ){scanf("%d%d", &x, &y);add(x, y), add(y, x);}bfs();for (int i = 1; i <= n; ++ i ) {if (cnt[i] == 0x3f3f3f3f) puts("0");else printf("%d\n", cnt[i]);}return 0;
}

---

383. 观光

383. 观光 - AcWing题库

由于无负权边，所以用dijkstra更新最短路，同时维护最短路条数
但是题目还要维护最短路条数，所以这里用了个类似拯救大兵瑞恩的思想：状压
dis[i][0]表最短路距离，dis[i][1]表示次短路距离，由于次短路的更新也具有拓扑序，所以我们可以在更新次短路的时候维护次短路条数

$dis[i][1]$如何计算？与i相连的所有点的最短路以及次短路中，第二大的数
代码体现在：
若dis[y][0] > dis[x][0] + w[i]，则更新最短路$dis[y][0]$，那么最短路成为次短路$dis[y][1]$，更新次短路，同时更新最短路
若dis[y][0] == dis[x][0] + w[i]，那么最短路条数累加，cnt[y][0] += cnt[x][0]
若dis[y][1] > dis[x][0] + w[i]，那么更新次短路$dis[y][1]$
若dis[y][1] == dis[x][0] + w[i]，那么次短路条数累加，cnt[y][1] += cnt[x][1]

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;const int N = 1010, M = 10010;
int h[N], e[M], ne[M], w[M], idx;
int n, m, s, t;
int dis[N][2], cnt[N][2]; bool st[N][2];struct Ver
{int x, d, type;bool operator>(const Ver& v) const // 建小堆重载>{return d > v.d;}
};void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}int dijkstra()
{memset(dis, 0x3f, sizeof(dis));memset(st, 0, sizeof(st));memset(cnt, 0, sizeof(cnt));priority_queue<Ver, vector<Ver>, greater<Ver>> q;q.push({s, 0, 0});dis[s][0] = 0, cnt[s][0] = 1;while (q.size()){auto t = q.top(); q.pop();int x = t.x, d = t.d, type = t.type;int count = cnt[x][type];if (st[x][type]) continue;st[x][type] = true;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (dis[y][0] > d + w[i]){dis[y][1] = dis[y][0], cnt[y][1] = cnt[y][0];q.push({y, dis[y][1], 1});dis[y][0] = d + w[i], cnt[y][0] = count;q.push({y, dis[y][0], 0});}else if (dis[y][0] == d + w[i]) cnt[y][0] += count;else if(dis[y][1] > d + w[i]){dis[y][1] = d + w[i], cnt[y][1] = count;q.push({y, dis[y][1], 1});}else if (dis[y][1] == d + w[i]) cnt[y][1] += count;}}int res = cnt[t][0];if (dis[t][0] + 1== dis[t][1]) res += cnt[t][1];return res;
}int main()
{int T;scanf("%d", &T);while ( T -- ){idx = 0;memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);int x, y, d;while ( m -- ){scanf("%d%d%d", &x, &y, &d);add(x, y, d);}scanf("%d%d", &s, &t);printf("%d\n", dijkstra());}return 0;
}