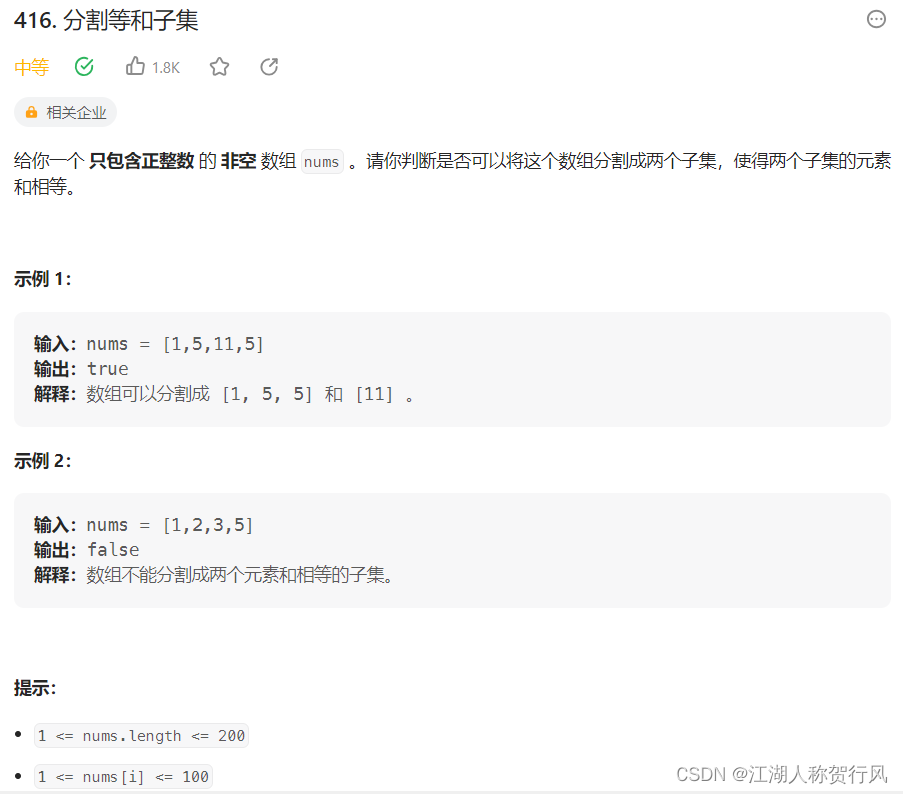
力扣 416. 分割等和子集
题目来源:https://leetcode.cn/problems/partition-equal-subset-sum/description/
C++题解(思路来源代码随想录) :
背包问题有多种背包方式,常见的有:01背包、完全背包、多重背包、分组背包和混合背包等等。一个商品如果可以重复多次放入是完全背包,而只能放入一次是01背包,本题中是01背包。
把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
以上分析完,我们就可以套用01背包,来解决这个问题了。
- 确定dp数组以及下标的含义。二维数组: dp[i][j]表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
- 确定递推公式。两种情况:不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。);放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值。所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])。
- dp数组初始化。一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。状态转移方程可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化,即i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。当 j < weight[0]的时候,dp[0][j] 应该是 0;当j >= weight[0]时,dp[0][j] 应该是value[0]。
- 确定遍历顺序。有两个遍历的维度:物品与背包重量。都可以! 但是先遍历物品更好理解。
- 举例推导dp数组。
class Solution {
public:bool canPartition(vector<int>& nums) {int len = nums.size();int sum = 0;for(int i = 0; i < len; i++) {sum += nums[i];}if(sum % 2 == 1) return false;vector<vector<int>> dp(len, vector<int>(sum/2+1, 0));for(int ii = nums[0]; ii <= sum/2; ii++) {dp[0][ii] = nums[0];}// 相当于包容量为sum/2,在len个物品中挑选,能装满则返回true。// 表示从0-j的元素中,取出和小于k的最大值。for(int j = 1; j < len; j++) {for(int k = 0; k <= sum/2; k++) {if(k < nums[j]) dp[j][k] = dp[j-1][k];else dp[j][k] = max(dp[j-1][k], dp[j-1][k-nums[j]]+nums[j]);}}if(dp[len-1][sum/2] == sum/2) return true;else return false;}
};# 使用一维dp数组(滚动数组)
在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组)。这就是滚动数组的由来,需要满足的条件是上一层可以重复利用,直接拷贝到当前层。
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
注意:遍历顺序必须先遍历物品再遍历包容量,且更新内层for循环需要递减(从后往前),因为滚动数组的更新需要用到未更新的前面元素,如果是递增(从前往后),前面更新的元素会影响后面的元素。
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;// dp[i]中的i表示背包内总和// 题目中说:每个数组中的元素不会超过 100,数组的大小不会超过 200// 总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了vector<int> dp(10001, 0);for (int i = 0; i < nums.size(); i++) {sum += nums[i];}// 也可以使用库函数一步求和// int sum = accumulate(nums.begin(), nums.end(), 0);if (sum % 2 == 1) return false;int target = sum / 2;// 开始 01背包for(int i = 0; i < nums.size(); i++) {for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}// 集合中的元素正好可以凑成总和targetif (dp[target] == target) return true;return false;}
};相关文章:

力扣 416. 分割等和子集
题目来源:https://leetcode.cn/problems/partition-equal-subset-sum/description/ C题解(思路来源代码随想录) : 背包问题有多种背包方式,常见的有:01背包、完全背包、多重背包、分组背包和混合背包等等。…...
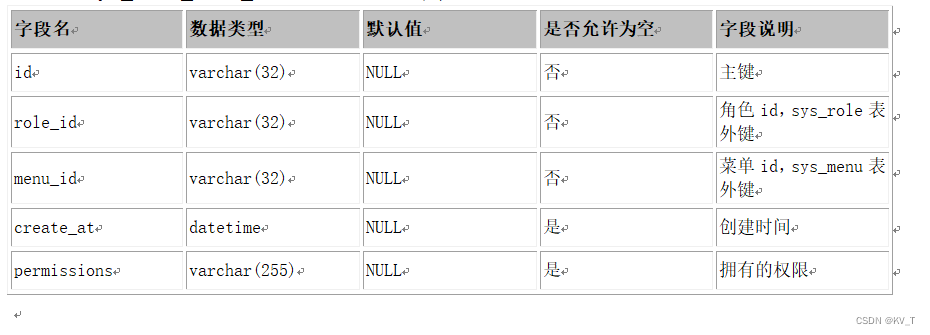
sqlyog导出mysql数据字典
1.打开sqlyog执行sql获取字典数据 SELECTt.COLUMN_NAME AS 字段名,t.COLUMN_TYPE AS 数据类型,CASE IFNULL(t.COLUMN_DEFAULT,Null) WHEN THEN 空字符串 WHEN Null THEN NULL ELSE t.COLUMN_DEFAULT END AS 默认值,CASE t.IS_NULLABLE WHEN YES THEN 是 ELSE 否 END AS 是否…...
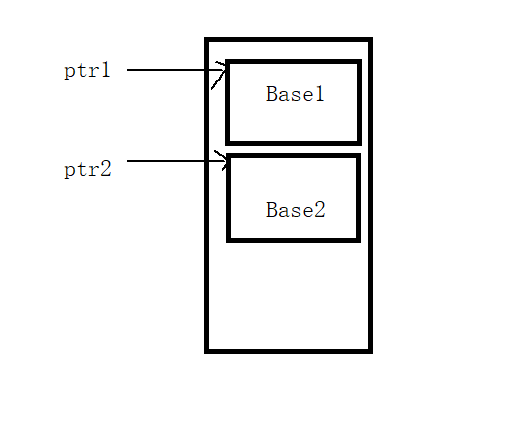
【C++】多态的实现及其底层原理
个人主页:🍝在肯德基吃麻辣烫 我的gitee:gitee仓库 分享一句喜欢的话:热烈的火焰,冰封在最沉默的火山深处。 文章目录 前言一、什么是多态?二、多态的构成条件2.1什么是虚函数?2.2虚函数的重写2…...

【网络编程】TCP带外数据总结
文章目录 一、带外数据基本知识二、带外数据的读写三、检测带外数据是否到达3.1、select上的异常事件3.2、SIGURG信号 四、带外标记 一、带外数据基本知识 带外数据(Out Of Band,OOB),用于迅速通告对方本端发生的重要事件…...

高薪程序员面试题精讲系列133之微服务里的网关有哪些实现方案?你熟悉Gateway网关吗?
一. 面试题及剖析 1. 今日面试题 微服务里的网关有哪些实现方案? Gateway网关是怎么实现的? 你用过Gateway网关吗? Gateway里有哪些路由规则? 2. 题目剖析 在上一篇文章中,壹哥给大家梳理了微服务里的远程调用、熔断等相关的面试题。今天这篇文章,壹哥会重点给大家梳理…...
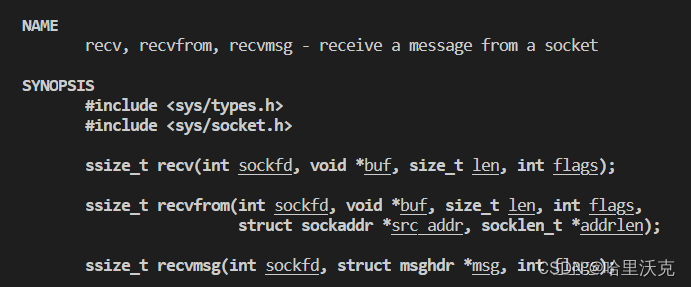
计算机网络(4) --- 协议定制
计算机网络(3) --- 网络套接字TCP_哈里沃克的博客-CSDN博客https://blog.csdn.net/m0_63488627/article/details/132035757?spm1001.2014.3001.5501 目录 1. 协议的基础知识 TCP协议通讯流程 编辑 2.协议 1.介绍 2.手写协议 1.内容 2.接口 …...
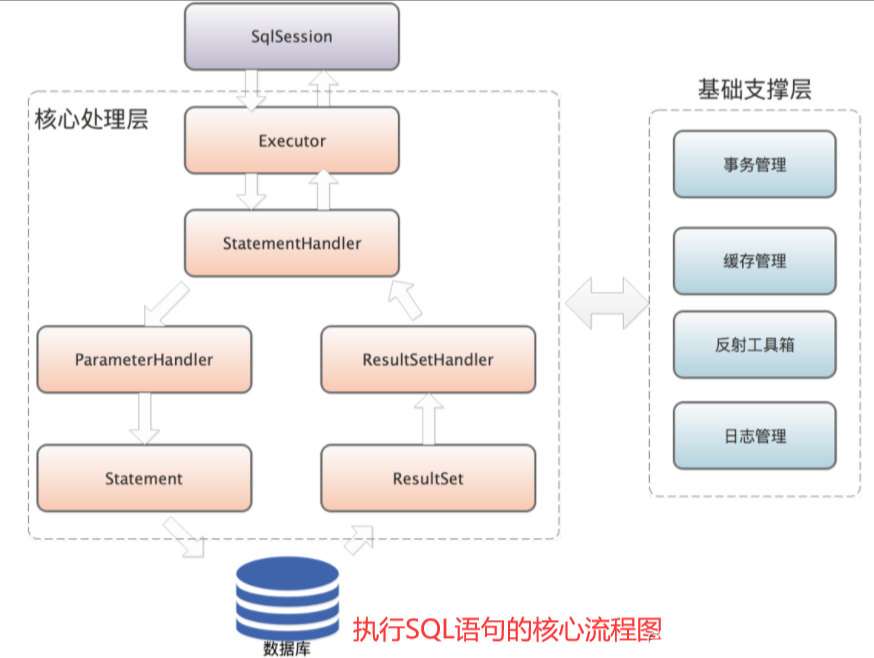
【Mybatis】Mybatis架构简介
文章目录 1.整体架构图2. 基础支撑层2.1 类型转换模块2.2 日志模块2.3 反射工具模块2.4 Binding 模块2.5 数据源模块2.6缓存模块2.7 解析器模块2.8 事务管理模块 3. 核心处理层3.1 配置解析3.2 SQL 解析与 scripting 模块3.3 SQL 执行3.4 插件 4. 接口层 1.整体架构图 MyBatis…...
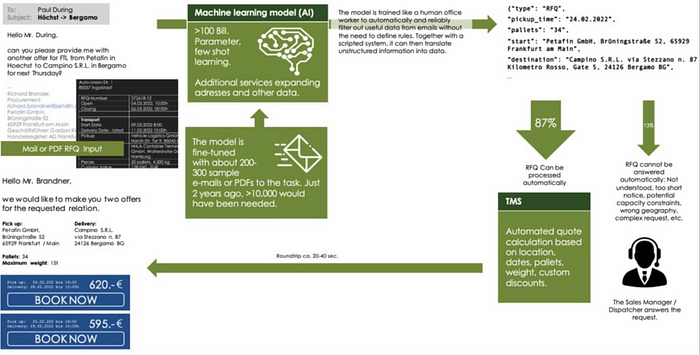
如何使用大模型处理生活繁琐的工作
如果每封电子邮件、每个带有订单、发票、投诉、录用请求或工作申请的 PDF 都可以翻译成机器可读的数据,会怎样?然后可以由 ERP / CRM / LMS / TMS 自动处理吗?无需编程特殊接口。 听起来很神奇?它确实有一些魔力。但最近已成为可…...

RpcController作用浅析
RpcController作用浅析 前面提到了RpcConsumer的实现思路,但是并没说明RpcController有什么作用,不妨看看google::protobuf::RpcController: class PROTOBUF_EXPORT RpcController {public:inline RpcController() {}virtual ~RpcControlle…...
Linux(三):Linux服务器下日常实操命令 (常年更新)
基础命令 cd命令:切换目录 cd :切换当前目录百至其它目录,比如进入/etc目录,则执行 cd /etccd / :在Linux 系统中斜杠“/”表示的是根目录。cd / ,即进入根目录.cd ~:进入用户在该系统的home目录&#…...

强大的截图软件--Snipaste
这里写目录标题 前言Snipaste贴图并置顶标注功能 下载 前言 在工作中,我们经常需要保存当前屏幕的图片,虽然系统总是会自带一些截图工具,但似乎用起来总是不那个顺手,例如我们需要对图片进行一些标注,或者将图片贴在屏…...
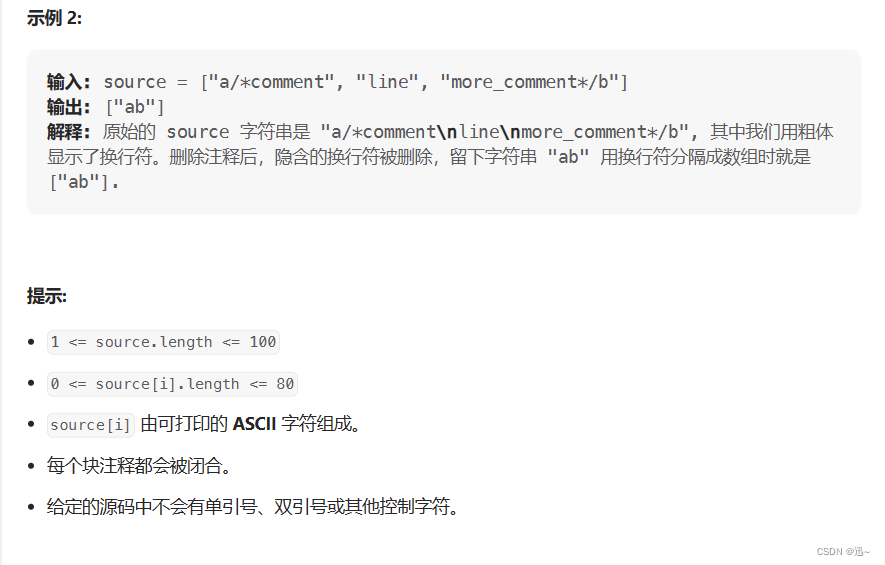
LeetCode·每日一题·722. 删除注释·模拟
题目 示例 思路 题意 -> 给定一段代码,将代码中的注释删除并返回。 由于注释只有两种类型: 字符串// 表示行注释,表示//和其右侧的其余字符应该被忽略。字符串/* 表示一个块注释,它表示直到下一个(非重叠&#x…...
npm更新和管理已发布的包
目录 1、更改包的可见性 1.1 将公共包设为私有 编辑 使用网站 使用命令行 1.2 将私有包公开 使用网站 使用命令行 2、将协作者添加到用户帐户拥有的私有包 2.1 授予对Web上私有用户包的访问权限 2.2 从命令行界面授予私有包访问权限 2.3 授予对私有组织包的访问权限…...

如何高效使用Gherkin
背景 时间回到2022年,我参与了一个使用了Flutter技术构建的Web前端项目。在这个项目上,我们小组的目标是实施Flutter前端自动化测试。 彼时,Flutter 2.x刚在Web端发力不久,Flutter Web上的应用和生态才刚刚开始,而在…...

[CKA]考试之调度 pod 到指定节点
由于最新的CKA考试改版,不允许存储书签,本博客致力怎么一步步从官网把答案找到,如何修改把题做对,下面开始我们的 CKA之旅 题目为: Task 创建一个Pod,名字为nginx-kusc00401,镜像地址是nginx…...
git 常用命令有哪些
Git 是我们开发工作中使用频率极高的工具,下面总结下他的基本指令有哪些,顺便温习一下。 前言 一般项目中长存2个分支: 主分支(master) 和开发分支(develop) 项目存在三种短期分支 ࿱…...
)
算法leetcode|66. 加一(rust重拳出击)
文章目录 66. 加一:样例 1:样例 2:样例 3:提示: 分析:题解:rust:go:c:python:java: 66. 加一: 给定一个由 整数 组成的 非…...

MySQL备份Shell脚本
将此脚本添加到crontab计划中,自动留存最新的两份备份 #!/bin/bash # 数据库配置 DB_HOST"localhost" DB_USER"root" DB_PASS"Sxbdc123!#" DB_NAME"ww"# 备份目录 BACKUP_DIR"/opt/mysqlbak"# 备份文件名称 BA…...

Python批量查字典和爬取双语例句
最近,有网友反映,我的批量查字典工具换到其它的网站就不好用了。对此,我想说的是,互联网包罗万象,网站的各种设置也有所不同,并不是所有的在线字典都可以用Python爬取的。事实上,很多网站为了防…...

uni-app、H5实现瀑布流效果封装,列可以自定义
文章目录 前言一、效果二、使用代码三、核心代码总结前言 最近做项目需要实现uni-app、H5实现瀑布流效果封装,网上搜索有很多的例子,但是代码都是不够完整的,下面来封装一个uni-app、H5都能用的代码。在小程序中,一个个item渲染可能出现问题,也通过加锁来解决问题。 一、…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
