C语言的_Bool类型
C99 新增了 _Bool 类型,用于表示布尔值,即逻辑值 true 和 false。
_Bool 类型也是一种整数类型。
原则上 _Bool 类型只占用一位存储空间。
C语言将非 0 的数当为 true,0 当为 false。
代码示例:
#include<stdio.h>
int main(void)
{int beep=11;if (beep){printf("1\n");}else{printf("2\n");}return 0;
}
结果:
1
代码示例:
#include<stdio.h>
int main(void)
{int beep=0;if (beep){printf("1\n");}else{printf("2\n");}return 0;
}
结果:
2
相关文章:

C语言的_Bool类型
C99 新增了 _Bool 类型,用于表示布尔值,即逻辑值 true 和 false。 _Bool 类型也是一种整数类型。 原则上 _Bool 类型只占用一位存储空间。 C语言将非 0 的数当为 true,0 当为 false。 代码示例: #include<stdio.h> int…...

【python爬虫】获取某一个网址下面抓取所有的a 超链接下面的内容
import requests as rq from bs4 import BeautifulSoup as bs import re# rooturl是传的是我需要查询和抓取的一个网址,可以是html js 等 def gethtml(rooturl, encoding"utf-8"):#默认解码方式utf-8response rq.get(rooturl)response.encoding encodin…...

AutoDL从0到1搭建stable-diffusion-webui
前言 AI绘画当前非常的火爆,随着Stable diffusion,Midjourney的出现将AI绘画推到顶端,各大行业均受其影响,离我们最近的AI绘画当属Stable diffusion,可本地化部署,只需电脑配备显卡即可完成AI绘画工作&…...

手动调整broker扩容后的旧topic分区
在broker扩容了两台机器之后,想让旧topic:quickstart76-events的分区也能铺满broker 1、创建一个topics-to-move.json json文件 $ vim topics-to-move.json json {"topics": [{"topic":"quickstart76-events"}],"v…...
)
【LeetCode-简单】剑指 Offer 25. 合并两个排序的链表(详解)
题目 入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。 示例1: 输入:1->2->4, 1->3->4 输出:1->1->2->3->4->4 本题与主站 21 题相同:力扣 题目地址&#x…...
Java版工程行业管理系统源码-专业的工程管理软件-em提供一站式服务
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目…...

【Spring】简化事件的使用,Spring提供了2种使用方式
Spring中事件可以配置顺序,利用线程池还可以做异步线程通知。怎么样使用事件?Spring简化事件的使用,Spring提供了2种使用方式:面向接口和面向EventListener注解。 1,面相接口的方式 案例 发布事件 需要先继承ApplicationEventP…...

探究Spring事务:了解失效场景及应对策略
在现代软件开发中,数据的一致性和完整性是至关重要的。为了保证这些特性,Spring框架提供了强大的事务管理机制,让开发者能够更加自信地处理数据库操作。然而,事务并非银弹,存在一些失效的情景,本文将带您深…...

Maven Manifold 条件编译
Maven 配置 通过 Maven 的不同 profile 实现不同环境传递不同符号。另外 lombok 可以 manifold 一同使用,见下方配置。 <properties><maven.compiler.source>8</maven.compiler.source><maven.compiler.target>8</maven.compiler.targ…...

4.数组与基本数学函数
一、数组 1.概念 数组是存放相同类型对象的容器,数组中存放的对象没有名字,而是要通过其所在的位置访问。数组中的每一个元素都相当于一个普通的变量,可以和普通变量一样进行赋值操作。 数组可以帮助我们批量地处理相同数据类型的相关数据…...

python与深度学习(十六):CNN和宝可梦模型二
目录 1. 说明2. 宝可梦模型的CNN模型测试2.1 导入相关库2.2 加载模型2.3 设置保存图片的路径2.4 加载图片2.5 数据处理和归一化2.6 对图片进行预测2.7 显示图片 3. 完整代码和显示结果4. 多张图片进行测试的完整代码以及结果 1. 说明 本篇文章是对上篇文章宝可梦模型训练的模型…...

PTA 1030 Travel Plan
个人学习记录,代码难免不尽人意。 A traveler’s map gives the distances between cities along the highways, together with the cost of each highway. Now you are supposed to write a program to help a traveler to decide the shortest path between his/h…...
MFC、Qt、WPF?该用哪个?
MFC、Qt和WPF都是流行的框架和工具,用于开发图形用户界面(GUI)应用程序。选择哪个框架取决于你的具体需求和偏好。MFC(Microsoft Foundation Class)是微软提供的框架,使用C编写,主要用于Windows…...

使用logback记录日志
1. Pom引用依赖 <dependency> <groupId>ch.qos.logback</groupId> <artifactId>logback-classic</artifactId> <version>1.2.11</version> </dependency> 2. logback.xml <?xml version"1.0" encoding"U…...
企业工程项目管理系统源码(三控:进度组织、质量安全、预算资金成本、二平台:招采、设计管理) em
工程项目管理软件(工程项目管理系统)对建设工程项目管理组织建设、项目策划决策、规划设计、施工建设到竣工交付、总结评估、运维运营,全过程、全方位的对项目进行综合管理 工程项目各模块及其功能点清单 一、系统管理 1、数据字典&#…...
【安装】XMind2022XMind2020安装教程(资源)
Xmind是一个制作思维导图很便利的软件。 1.资源链接 Xmind2022: 链接:https://pan.baidu.com/s/1j4DFedxxX2YJ3HBy1-MpHw?pwdxmin 提取码:xmin Xmind2020: 链接:https://pan.baidu.com/s/1wNqMApuy0yoBF2CvpBDpDA?pwdxmin 提取码&#x…...
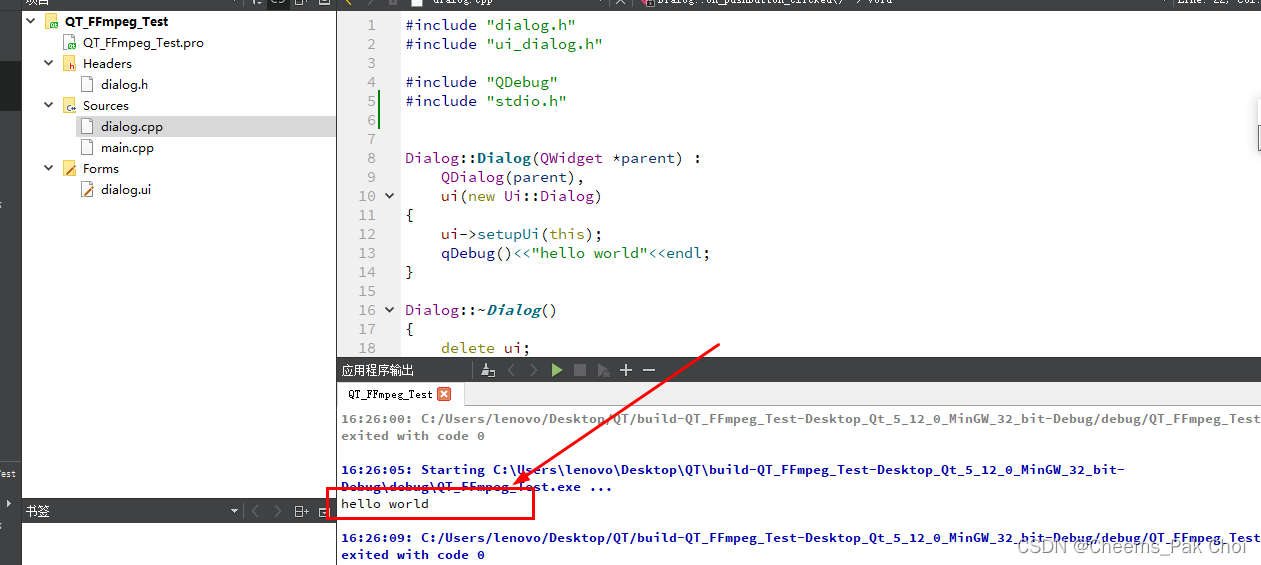
Windows下QT Creator安装MinGW 32bit编译器
前言 注:本作者是基于FFmpeg开发需要,故在Windows下QT Creator中安装MinGW 32bit编译器!其它型号编译器参照此文章基本可以实现! 一、下载需要的编译器 1、下载链接 链接: 链接:https://pan.baidu.com/…...
Emacs之解决键值绑定冲突问题(一百二十三)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

瞄准产业应用,大模型加持的深兰科技AI虚拟数字人落地业务场景
伴随ChatGPT的问世,在技术与商业运作上都日渐发展成熟的AI数字人产业正持续升温。 目前的AI数字人不仅拥有超高“颜值”,同时还拥有更为丰富的、细腻的表情和动作。更有甚者,AI数字人已经具备自定义构建知识图谱、自主对话、不断学习成长的能…...
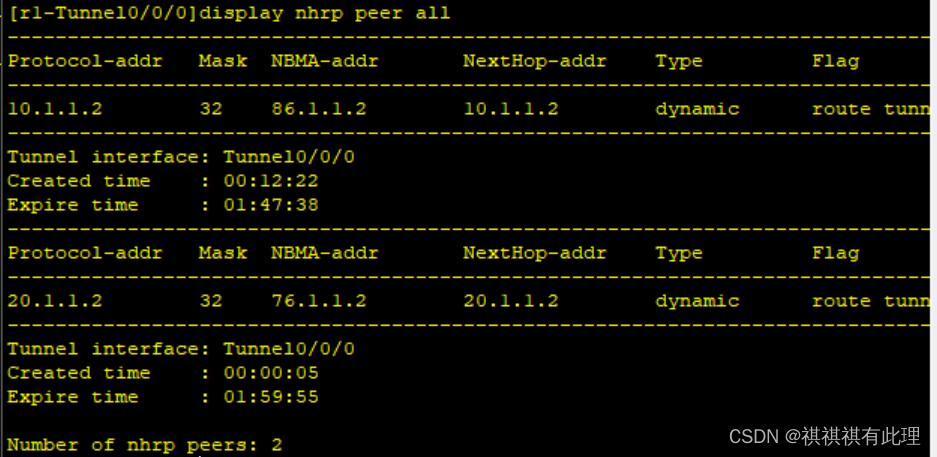
【网络基础进阶之路】基于MGRE多点协议的实战详解
PS:本要求基于华为的eNSP模拟软件进行 具体要求: 完成步骤: 1、根据上述要求,对各路由器进行地址安排,如下图。 2、进入各路由器,对每个端口进行地址设置。 R1路由器设置: ISP路由器设置&…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
