华为OD机试 - 检查数组中是否存在满足规则的数组组合1（Python）
相关文章：
华为OD机试 - 检查数组中是否存在满足规则的数组组合1（Python）
检查数组中是否存在满足规则的数组组合1 题目 给定一个正整数数组 检查数组中是否存在满足规则的数组组合 规则： A = B + 2C 输入 第一行输出数组的元素个数 接下来一行输出所有数组元素，用空格隔开 输出 如果存在满足要求的数 在同一行里依次输出规则里A B C的取值，用…...
深圳“托育”放大招！政府出钱帮你带娃啦！
工作忙得不可开交 难以照料孩子的起居 这个带娃难题常常让双职工家庭 感觉到头疼不已 一边是工作，一边是孩子 父母都上班，宝宝谁来带？ 未来这个问题将迎刃而解！ 因为政府要出钱帮你带娃啦！ 近日，深圳市总工…...
服务间调用方式 OpenFeign 的介绍和使用
文章目录前言1、 RestTemplate1.1、通用方法 exchange1.2、RestTemplate 和 OpenFeign 的区别2、RPC 和 HTTP2.1、RPC 是什么2.2、RPC 调用过程示意图2.3、HTTP 是什么2.4、HTTP 调用过程示意图2.5、对比3 、OpenFeign3.1 、OpenFeign 常用注解3.2 、案例前言 Feign 停更了&am…...
从开始测试到年薪40W，我的自动化测试艰辛历程
我希望我的故事能够激励现在的软件测试人，尤其是还坚持在做“点点点”的测试人。 你可能会有疑问：“我也能做到这一点的可能性有多大？”因此，我会尽量把自己做决定和思考的过程讲得更具体一些，并尽量体现更多细节。 …...
《C++ Primer Plus》第17章：输入、输出和文件（1）
对C输入和输出（简称I/O）的讨论提出了一个问题。一方面，几乎每个程序都要使用输入和输出，因此了解如何使用它们是每个学习计算机语言的人面临的首要任务；另一方面，C使用了很多较为高级的语言特性来实现输入和…...
静态代码审计插件 snyk 使用教程
目录 1、vscode 插件安装 2、手动生成 token 3、自动分析 1、vscode 插件安装 2、手动生成 token 点击登录链接：...
从“服务”，到“赋能”，日日顺再次定义供应链生态建设
在众多不确定因素的交织下，当下的供应链企业变革呈现出前所未有的紧迫感。一体化、全链路的趋势，为企业的发展指明方向，与此同时数字化与科技化开始承托供应链管理能力的升级与变革。 2月15日，由日日顺供应链、运联智库联合举办的…...
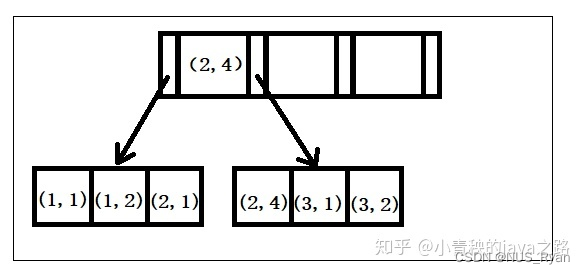
MySQL(一):B+ Tree,索引以及其优点, 索引实战, 聚簇索引和非聚簇索引, 最左匹配,索引失效
文章目录一、B TreeB Tree相比于红黑树的优点1. B树有更低的树高2. B树更符合磁盘访问原理二、MySQL索引2.1 B Tree索引2.2 哈希索引2.3 全文索引2.4 空间数据索引三、索引的优点以及什么时候需要使用索引什么时候需要使用索引四、索引实战建立普通索引建立唯一索引建立主键索引…...
06：进阶篇 - Hello，CTK！
作者： 一去、二三里 个人微信号： iwaleon 微信公众号： 高效程序员 在接触任何语言时，我们总能看到“Hello,World!"，它的中文意思是“你好，世界！”。由于简洁、实用，所以非常著名。 为了延续这个优良传统并迎接 CTK，在演示第一个插件时，我们使用“Hello,CTK!&qu…...
SpringCloud(一)注册中心
注册中心eureka服务端客户端负载均衡nacos服务端客户端nacos分级存储模型配置集群属性nacos环境隔离-namespace临时实例和非临时实例Eureka和Nacos的异同负载均衡策略饥饿加载eureka 服务端 依赖 <!-- eureka注册中心服务端依赖--><dependencies><depe…...
centos7环境配置
Python Centos7中自带的python2，如果要是用python3，就需要自己安装了，因为yum源中没有python3，需要下载包进行源码编译安装。 安装步骤 1、安装python3相关依赖包 yum -y install zlib-devel bzip2-devel openssl-devel nc…...
如何解锁华为手机PIN/图案/指纹/人脸锁？
您的手机存储主要数据，因此为您的设备设置安全代码让您高枕无忧。屏幕和生物识别锁可在手机丢失时保护您的手机，并使其在被盗时无法访问。每次您需要密码来解锁手机时，但如果您被锁在密码之外怎么办？ 今天的话题将独家帮助华为用…...
物理层基本介绍
corset 0 告诉下行初始带宽是多少 initail DL BWP, 4g 是20M带宽，5G是FR1 如果5G是全带宽的话，手机很快就会没电了。 告诉手机带宽会分布在某一个带宽里面去，将手机的带宽调整就行。 DCI，告诉手机，未来的某一个时刻&a…...
数据库原理及应用期末复习汇总(附某高校期末真题试卷)
文章目录《数据库原理及应用》试题1一、选择题（共35分）二、填空（每空1分，共20分）三、T-SQL综合题(共35分)四、综合应用题(共10分)《数据库原理及应用》试题2一、选择题（共35分）二、填空…...
mummerplot gnuplot 安装（nucmer）
可用ref：https://blog.sciencenet.cn/home.php?modspace&uid2970729&doblog&id1174911 下载稳定老版本gnuplot v4.6.2 mkdir gnuplot && cd gnuplot wget https://sourceforge.net/projects/gnuplot/files/gnuplot/4.6.2/gnuplot-4.6.2.tar…...
怎样做校园外卖配送系统创业？打造一体化服务校园平台如何进行？
在大学校园里，兼职赚钱、勤工俭学、自主创业是一种普遍现象。如今，大学校园在大力支持在校生自主创业。比如用校园外卖配送系统创业，不仅可以丰富校园生活，接触人和事，还可以积累经验。 怎样做校园外卖配送系统平台&am…...
MySQL(三):切分，主从复制，读写分离
文章目录一、切分水平切分垂直切分水平切分策略二、主从复制三、读写分离一、切分 水平切分 水平切分又称为sharding,它是将同一个表中的记录拆分到多个结构相同的表中。当一个表的数据不断增多的时候，sharding是必然的选择，它可以将数据分布到集群的不…...
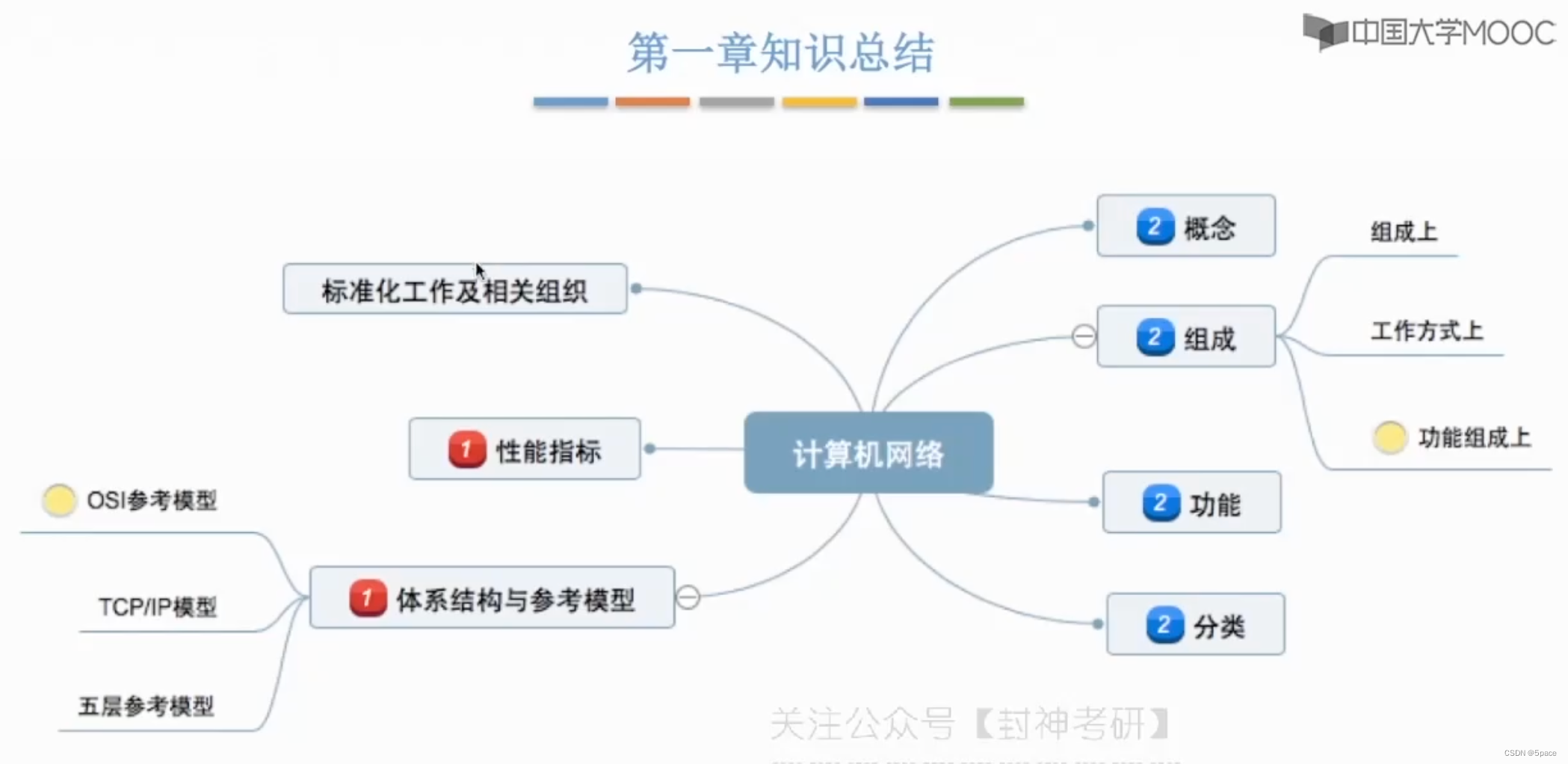
王道考研——计算机网络（第一章 计算机网络体系结构）
1.0认识计算机网络 在下载电影（不会出现乱序问题）和微信收发消息（比如表情包乱序了）所使用的协议是不同的 1.1-1概念和功能 （1）计算机网络的概念 （2）计算机网络的功能 （…...
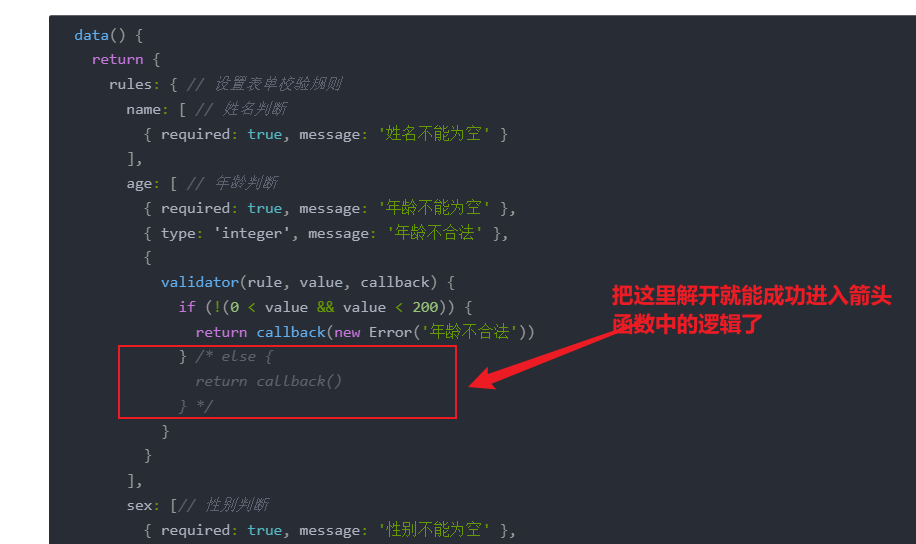
ElementUI中为什么使用this.$refs.form.validate验证成功却直接跳过
ElementUI中为什么使用this.$refs.form.validate验证成功却直接跳过 问题背景 在写一个Vue练手项目时，我使用rulse对表单中用户输入的数据进行校验，但莫名奇妙就发现：当我点击提交表单时，表单中的数据都验证成功了，但是…...
全期望值定理与全方差定理
全期望值定理（law of total expectation）比较熟悉，竟然还有个全方差定理（law of total variance），关于条件期望与条件方差的，总结一下。 1. 全期望值定理 随机变量 XXX 关于另外一个随机变量 …...
内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤： 1）请求大小调整：首先，malloc 需要调整用户请求的大小，以适应内部数据结构（例如，可能需要存储额外的元数据）。通常，这包括对齐调整，确保分配的内存地址满足特定硬件要求（如对齐到8字节或16字节边界）。 2）空闲…...
地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波：可以用来解决所提出的地质任务的波；干扰波：所有妨碍辨认、追踪有效波的其他波。 地震勘探中，有效波和干扰波是相对的。例如，在反射波…...
阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...
无法与IP建立连接，未能下载VSCode服务器
如题，在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈，发现是VSCode版本自动更新惹的祸！！！ 在VSCode的帮助->关于这里发现前几天VSCode自动更新了，我的版本号变成了1.100.3 才导致了远程连接出…...
（二）TensorRT-LLM | 模型导出（v0.20.0rc3）
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述，后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作，其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...
从深圳崛起的“机器之眼”：赴港乐动机器人的万亿赛道赶考路
进入2025年以来，尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断，但全球市场热度依然高涨，入局者持续增加。 以国内市场为例，天眼查专业版数据显示，截至5月底，我国现存在业、存续状态的机器人相关企…...
el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
（二）原型模式
原型的功能是将一个已经存在的对象作为源目标，其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现，忽略对象创建过程中的其它细节。 📌 核心特点： 避免重复初…...
第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用，通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试，通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
三体问题详解
从物理学角度，三体问题之所以不稳定，是因为三个天体在万有引力作用下相互作用，形成一个非线性耦合系统。我们可以从牛顿经典力学出发，列出具体的运动方程，并说明为何这个系统本质上是混沌的，无法得到一般解…...