【深度学习_TensorFlow】感知机、全连接层、神经网络
写在前面
感知机、全连接层、神经网络是什么意思?
感知机: 是最简单的神经网络结构,可以对线性可分的数据进行分类。
全连接层: 是神经网络中的一种层结构,每个神经元与上一层的所有神经元相连接,实现全连接。
神经网络: 是由大量神经元组成的网络结构,通过层与层之间的连接,实现对数据的表示和转换。神经网络通常由输入层、隐藏层和输出层等全连接层构成。
三者有什么关系?
-
感知机是最简单的单层神经网络,仅有输入层和输出层。
-
全连接层是构建多层神经网络时常用的一种层类型。
-
神经网络通常由多层的全连接层叠加构成,从而实现比单层感知机更强大的功能。
所以可以说,感知机是简单的神经网络,全连接层是构建复杂神经网络的基础模块,神经网络通过组合多层全连接层实现复杂的功能。感知机和全连接层都是神经网络的组成要素。
写在中间
一、感知机
感知机(Perceptron)是一种简单的人工神经网络,由Frank Rosenblatt于1957年提出。它是一种线性二分类模型,主要用于解决二元分类问题。感知机的基本结构包括输入层、输出层和一个线性分类器。输入层接收输入数据,输出层提供分类结果,线性分类器将输入数据映射到输出层。
感知机模型的结构如下,它接受长度为𝑛的一维向量𝒙 = [𝑥1, 𝑥2, … , 𝑥𝑛],每个输入节点通过权值为[w1, w2, … , w𝑛]的连接汇集为变量 𝑧
z = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b z=w_{1}x_{1}+w_{2}x_{2}+\cdots+w_{n}x_{n}+b z=w1x1+w2x2+⋯+wnxn+b
写为向量的形式为:
z = w T x + b z=w^{\mathrm{T}}x+b z=wTx+b
其中𝑏称为感知机的偏置(Bias),一维向量𝒘 = [𝑤1, 𝑤2, … , 𝑤𝑛]称为感知机的权值(Weight),𝑧 称为感知机的净活性值(Net Activation)。
感知机是线性模型,并不能处理线性不可分问题。通过在线性模型后添加激活函数后得到活性值(Activation) :
a = σ ( z ) = σ ( w T x + b ) a=\sigma(z)=\sigma(w^{\mathrm{T}}x+b) a=σ(z)=σ(wTx+b)
其中激活函数可以是阶跃函数,也可以是符号函数:
a = { 1 w T x + b ≥ 0 0 w T x + b < 0 a=\left\{\begin{matrix}1&w^\mathrm{T}x+b\geq0\\0&w^\mathrm{T}x+b<0\end{matrix}\right. a={10wTx+b≥0wTx+b<0
a = { 1 w T x + b ≥ 0 − 1 w T x + b < 0 a=\left\{\begin{matrix}1&\text{w}^\mathrm{T}x+b\geq0\\-1&\text{w}^\mathrm{T}x+b<0\end{matrix}\right. a={1−1wTx+b≥0wTx+b<0

二、全连接层
( 1 )了解概念
全连接层(Fully Connected Layer)是神经网络中的一种层结构,主要用于将前一层的输出与后一层的输入进行连接。全连接层中的每个神经元都与前一层的所有神经元相连,因此得名。它在感知机的基础上,将不连续的阶跃激活函数换成了其它平滑连续可导的激活函数,并通过堆叠多个网络层来增强网络的表达能力
我们通过替换感知机的激活函数,同时并行堆叠多个神经元来实现多输入、多输出的网络层结构。举一个最常用的例子:
构成 3 输入节点、2 个输出节点的网络层。其中第一个输出节点的输出为:
o 1 = σ ( w 11 ⋅ x 1 + w 21 ⋅ x 2 + w 31 ⋅ x 3 + b 1 ) o_1=\sigma(w_{11}\cdot x_1+w_{21}\cdot x_2+w_{31}\cdot x_3+b_1) o1=σ(w11⋅x1+w21⋅x2+w31⋅x3+b1)
第二个输出节点的输出为:
o 2 = σ ( w 12 ⋅ x 1 + w 22 ⋅ x 2 + w 32 ⋅ x 3 + b 2 ) o_{2}=\sigma(w_{12}\cdot x_{1}+w_{22}\cdot x_{2}+w_{32}\cdot x_{3}+b_{2}) o2=σ(w12⋅x1+w22⋅x2+w32⋅x3+b2)
输出向量为𝒐 = [𝑜1, 𝑜2],通过矩阵可以表达为如下的形式:
[ o 1 o 2 ] = [ x 1 x 2 x 3 ] @ [ w 11 w 12 w 21 w 22 w 31 w 32 ] + [ b 1 b 2 ] \begin{bmatrix}o_1&o_2\end{bmatrix}=\begin{bmatrix}x_1&x_2&x_3\end{bmatrix}@\begin{bmatrix}w_{11}&w_{12}\\w_{21}&w_{22}\\w_{31}&w_{32}\end{bmatrix}+\begin{bmatrix}b_1&b_2\end{bmatrix} [o1o2]=[x1x2x3]@ w11w21w31w12w22w32 +[b1b2]
可以归纳为
O = X @ W + b \boldsymbol{O}=X@W+\boldsymbol{b} O=X@W+b
输入矩阵𝑿的 shape 定义为 [ b , d i n ] [b, d_{in}] [b,din],𝑏为样本数量,此处只有 1 个样本参与前向运算, d i n d_{in} din为输入节点数;权值矩阵 W 的 shape 定义为 [ d i n , d o u t ] [d_{in}, d_{out}] [din,dout], d o u t d_{out} dout为输出节点数,偏置向量 b 的 shape 定义为 [ d o u t ] [d_{out}] [dout]。
( 2 )学会实现
全连接层本质上是矩阵的相乘和相加运算,实现并不复杂。TensorFlow 中有使用方便的层实现方式:layers.Dense(units, activation)。通过 layer.Dense 类,只需要指定输出节点数 units 和激活函数类型 activation 即可。
fc = layers.Dense(units=512, activation=tf.nn.relu)
上述通过一行代码即可以创建一层全连接层 fc,并指定输出节点数为 512,并创建内部权值张量𝑾和偏置张量𝒃。我们可以通过类内部的成员名 fc.kernel和 fc.bias来获取权值张量𝑾和偏置张量𝒃对象
三、神经网络
通过层层堆叠上面的全连接层,保证前一层的输出节点数与当前层的输入节点数匹配,,即可堆叠出任意层数的网络。我们把这种由神经元相互连接而成的网络叫做神经网络。
如图其中第 1~3 个全连接层在网络中间,称之为隐藏层 1、2、3,最后一个全连接层的输出作为网络的输出,称为输出层。隐藏层 1、2、3 的输出节点数分别为[256,128,64],输出层的输出节点数为 10。

下面我们就用张量的方式来实现上面的神经网络
# 隐藏层 1 张量
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
# 隐藏层 2 张量
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1))
b2 = tf.Variable(tf.zeros([128]))
# 隐藏层 3 张量
w3 = tf.Variable(tf.random.truncated_normal([128, 64], stddev=0.1))
b3 = tf.Variable(tf.zeros([64]))
# 输出层张量
w4 = tf.Variable(tf.random.truncated_normal([64, 10], stddev=0.1))
b4 = tf.Variable(tf.zeros([10])) 但是随着网络层数的增加,这样手动创建一个神经网络就显得过于繁琐,我们有更为简单的层实现方式,对于这种数据依次向前传播的网络,也可以通过 Sequential 容器封装成一个网络大类对象,调用大类的前向计算函数一次即可完成所有层的前向计算,使用起来更加方便:
# 导入 Sequential 容器
from keras import layers,Sequential # 通过 Sequential 容器封装为一个网络类
model = Sequential([ layers.Dense(256, activation=tf.nn.relu) , # 创建隐藏层 1 layers.Dense(128, activation=tf.nn.relu) , # 创建隐藏层 2 layers.Dense(64, activation=tf.nn.relu) , # 创建隐藏层 3 layers.Dense(10, activation=None) , # 创建输出层
]) out = model(x) # 前向计算得到输出
至此,网络构建的大体流程就讲解完毕了
写在最后
👍🏻点赞,你的认可是我创作的动力!
⭐收藏,你的青睐是我努力的方向!
✏️评论,你的意见是我进步的财富!
相关文章:

【深度学习_TensorFlow】感知机、全连接层、神经网络
写在前面 感知机、全连接层、神经网络是什么意思? 感知机: 是最简单的神经网络结构,可以对线性可分的数据进行分类。 全连接层: 是神经网络中的一种层结构,每个神经元与上一层的所有神经元相连接,实现全连接。 神经…...

软件测试(功能、接口、性能、自动化)详解
一、软件测试功能测试 测试用例编写是软件测试的基本技能;也有很多人认为测试用例是软件测试的核心;软件测试中最重要的是设计和生成有效的测试用例;测试用例是测试工作的指导,是软件测试的必须遵守的准则。 黑盒测试常见测试用…...

Oracle表段中的高水位线HWM
在Oracle数据的存储中,可以把存储空间想象为一个水库,数据想象为水库中的水。水库中的水的位置有一条线叫做水位线,在Oracle中,这条线被称为高水位线(High-warter mark, HWM)。在数据库表刚建立的时候&…...

【福建事业单位-推理判断】03类别推理
【福建事业单位-推理判断】03类别推理 一、类别推理1.1语义关系考点一、近义反义关系(不需要严格的,意思相近即可)近义反义的二级辨析(感情色彩)考点二:比喻义、象征义 1.2 逻辑关系1.2.1全同关系ÿ…...

Leetcode-每日一题【剑指 Offer 05. 替换空格】
题目 请实现一个函数,把字符串 s 中的每个空格替换成"%20"。 示例 1: 输入:s "We are happy."输出:"We%20are%20happy." 限制: 0 < s 的长度 < 10000 解题思路 前置知识 Str…...

zookeeper+kafka分布式消息队列集群的部署
目录 一、zookeeper 1.Zookeeper 定义 2.Zookeeper 工作机制 3.Zookeeper 特点 4.Zookeeper 数据结构 5.Zookeeper 应用场景 (1)统一命名服务 (2)统一配置管理 (3)统一集群管理 (4&…...

VR全景旅游,智慧文旅发展新趋势!
引言: VR全景旅游正在带领我们踏上一场全新的旅行体验。这种沉浸式的旅行方式,让我们可以足不出户,却又身临其境地感受世界各地的美景。 一.VR全景旅游是什么? VR全景旅游是一种借助虚拟现实技术,让用户…...

详解EMBER数据集中对PE文件提取ByteEntropyHistogram特征
1. 引入 在我们对PE文件提取特征时,经常会在PE特征工程的项目中,看到如下这段代码 class ByteEntropyHistogram(FeatureType): 2d byte/entropy histogram based loosely on (Saxe and Berlin, 2015).This roughly approximates the joint probability…...
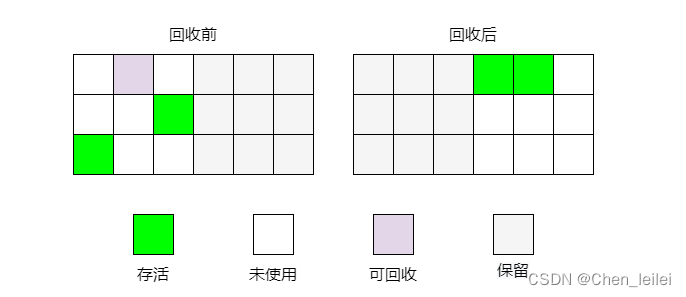
垃圾回收机制和常用的算法
一.什么是垃圾回收? 垃圾回收主要针对堆和方法区(非堆),程序计数器,虚拟机栈,本地方法栈这三个区域属于线程私有,随着线程的销毁,自然就会雄安会了,因此不需要堆着三个区域进行垃圾…...
【PostgreSQL】系列之 一 schema详解(二)
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_Linux,Java基础学习,大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的…...
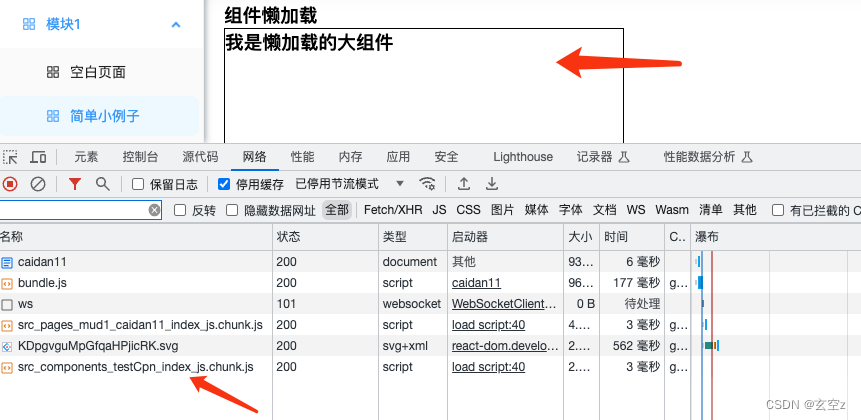
性能优化-react路由懒加载和组件懒加载
背景 随着项目越来越大,打包后的包体积也越来越大,严重影响了首屏加载速度,需要对路由和组件做懒加载处理 主要用到了react中的lazy和Suspense。 废话不多说,直接上干货 路由懒加载 核心代码 import React, { lazy, Suspens…...

静态网页加速器:优化性能和交付速度的 Node.js 最佳实践
如何使用 Node.js 发布静态网页 在本文中,我们将介绍如何使用 Node.js 来发布静态网页。我们将创建一个简单的 Node.js 服务器,将 HTML 文件作为响应发送给客户端。这是一个简单而灵活的方法,适用于本地开发和轻量级应用。 1、创建静态网页…...

Spring 非自定义Bean注解
Spring 非自定义Bean注解 1.概述 在xml中配置的Bean都是自己定义的, 例如:UserDaolmpl,UserServicelmpl。但是,在实际开发中有些功能类并不是我们自己定义的, 而是使用的第三方jar包中的,那么,…...
微信小程序:点击按钮实现数据加载(带模糊查询)
效果图 代码 wxml: <!-- 搜索框--> <form action"" bindsubmit"search_all_productiond"><view class"search_position"><view class"search"><view class"search_left">工单号:</view…...

2023-2029年中国烘焙工坊市场经营管理风险与未来竞争优势分析报告
2023-2029年中国烘焙工坊市场经营管理风险与未来竞争优势分析报告 ################################### 《报告编号》: BG460671 《出版时间》: 2023年8月 《出版机构》: 中智正业研究院 免费售后 服务一年,具体内容及订购流程欢迎咨询客服人员 内容简介&…...

用Rust实现23种设计模式之适配器
关注我,学习Rust不迷路 在 Rust 中,可以使用结构体和 trait 来实现适配器模式。适配器模式是一种结构型设计模式,它允许将一个类的接口转换为客户端所期望的另一个接口。下面是一个使用 Rust 实现适配器模式的示例,带有详细的注释…...
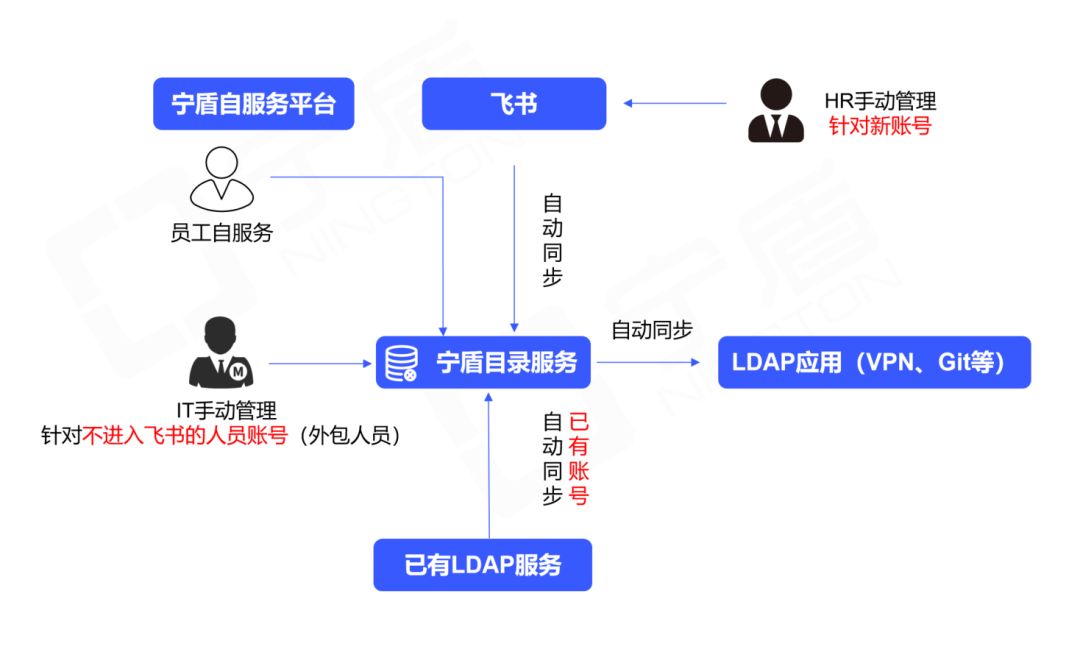
替换开源LDAP,西井科技用宁盾目录统一身份,为业务敏捷提供支撑
客户介绍 上海西井科技股份有限公司成立于2015年,是一家深耕于大物流领域的人工智能公司,旗下无人驾驶卡车品牌Q-Truck开创了全球全时无人驾驶新能源商用车的先河,迄今为止已为全球16个国家和地区,120余家客户打造智能化升级体验…...
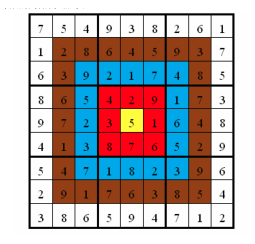
靶形数独
题目描述 小城和小华都是热爱数学的好学生,最近,他们不约而同地迷上了数独游戏,好胜的他们想用数独来一比高低。但普通的数独对他们来说都过于简单了,于是他们向 Z 博士请教,Z 博士拿出了他最近发明的“靶形数独”&am…...

C语言阶段性测试题
【前言】:本部分是C语言初阶学完阶段性测试题,最后一道编程题有一定的难度,需要多去揣摩,代码敲多了,自然就感觉不难了,加油,铁汁们!!! 一、选择题 1.下面程…...

java工厂设计模式
Java中的工厂设计模式是一种创建型设计模式,它提供了一种将对象的创建逻辑抽象出来的方法,使得客户端代码不需要直接实例化具体的类,而是通过一个共同的接口来创建对象。这样可以降低代码之间的耦合性,提高代码的可维护性和可扩展…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
