数据结构10 -查找_树表查找
-
创建二叉搜索树
二叉搜索树
二叉搜索树是有数值的了,二叉搜索树是一个有序树。
-
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
-
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
-
它的左、右子树也分别为二叉排序树
下面这两棵树都是搜索树

bstree.c(二叉搜索树)
#include <stdio.h>
#include <stdlib.h>
#define SIZE 10//二叉树节点
struct BSTree_node
{unsigned int elem;struct BSTree_node *ltree, *rtree; // 左右子树
};struct BSTree_node *create_bstree(unsigned int *pt, int n);
struct BSTree_node *insert_bstree(struct BSTree_node *T, unsigned int elem);
void in_order(struct BSTree_node *tree);int main(void)
{unsigned int num;unsigned int arr[SIZE] = {37, 22, 11, 82, 67, 9, 45, 91, 33, 52}; // 无序数组struct BSTree_node *mytree = NULL;mytree = create_bstree(arr, SIZE); // 创建二叉树in_order(mytree); // 中序遍历printf("\n");return 0;
}// 创建二叉搜索树
struct BSTree_node *create_bstree(unsigned int *pt, int n)
{struct BSTree_node *tree = NULL;for(int i = 0; i < n; i++){tree = insert_bstree(tree, *pt);pt++;}return tree;
}struct BSTree_node *insert_bstree(struct BSTree_node *T, unsigned int elem)
{if(!T){T = (struct BSTree_node *)malloc(sizeof(struct BSTree_node));T->elem = elem;T->ltree = T->rtree = NULL;}else if(elem < T->elem);{T->ltree = insert_bstree(T->ltree, elem); //递归}else if(elem > T->elem);{T->rtree = insert_bstree(T->rtree, elem); //递归}else{printf("inserting repeat node is fobidden.\n");exit(0);}return T;
}
// 遍历
void in_order(struct BSTree_node *tree)
{if(tree){in_order(tree->ltree);printf("%d", tree->elem);in_order(tree->rtree);}
}力扣题目
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。示例 1:

输入:root = [2,1,3]
输出:true示例 2:

输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
//递归1 ---》中序遍历 左 - 中 - 右,所以中序遍历应该是有序数组(单调递增)
class Solution {
private:vector<int> vec;void traversal(TreeNode* root) {if (root == NULL) return;traversal(root->left); // 左vec.push_back(root->val); // 中 // 将二叉搜索树转换为有序数组traversal(root->right); // 右}
public:bool isValidBST(TreeNode* root) {vec.clear(); // 不加这句在leetcode上也可以过,但最好加上traversal(root);for (int i = 1; i < vec.size(); i++) {// 注意要小于等于,搜索树里不能有相同元素if (vec[i] <= vec[i - 1]) return false;}return true;}
};//递归2 中序遍历
class Solution {
public:TreeNode* pre = NULL; // 用来记录前一个节点bool isValidBST(TreeNode* root) {if (root == NULL) return true; // 空二叉树属于任何是各种二叉树bool left = isValidBST(root->left); // 左if (pre != NULL && pre->val >= root->val) return false;pre = root; // 记录前一个节点bool right = isValidBST(root->right); // 右return left && right;}
};//迭代
class Solution {
public:bool isValidBST(TreeNode* root) {stack<TreeNode*> st;TreeNode* cur = root;TreeNode* pre = NULL; // 记录前一个节点while (cur != NULL || !st.empty()) {if (cur != NULL) {st.push(cur);cur = cur->left; // 左} else {cur = st.top(); // 中st.pop();if (pre != NULL && cur->val <= pre->val)return false;pre = cur; //保存前一个访问的结点cur = cur->right; // 右}}return true;}
};-
查找_添加二叉搜索树
二叉搜索树插入以及查找数值
bstree_find.c
#include <stdio.h>
#include <stdlib.h>
#define SIZE 10//二叉树节点
struct BSTree_node
{unsigned int elem;struct BSTree_node *ltree, *rtree; // 左右子树
};struct BSTree_node *create_bstree(unsigned int *pt, int n);
struct BSTree_node *insert_bstree(struct BSTree_node *T, unsigned int elem);
void in_order(struct BSTree_node *tree);int main(void)
{unsigned int num;unsigned int arr[SIZE] = {37, 22, 11, 82, 67, 9, 45, 91, 33, 52}; // 无序数组struct BSTree_node *mytree = NULL;mytree = create_bstree(arr, SIZE); // 创建二叉树in_order(mytree); // 中序遍历printf("\n");//查找printf("please enter a number you want to find in the BSTree:\n");scanf("%d", &num);if(search_bstree(mytree, num))printf("find %d in the mytree.\n", num);elseprintf("can't find %d in the mytree.\n", num); //插入printf("please enter a number you want to insert in the BSTree:\n");scanf("%d", &num);mytree = insert_bstree(mytree, num);in_order(mytree);printf("\n");return 0;
}// 创建二叉搜索树
struct BSTree_node *create_bstree(unsigned int *pt, int n)
{struct BSTree_node *tree = NULL;for(int i = 0; i < n; i++){tree = insert_bstree(tree, *pt);pt++;}return tree;
}
// 创建二叉搜索树插入节点
struct BSTree_node *insert_bstree(struct BSTree_node *T, unsigned int elem)
{if(!T){T = (struct BSTree_node *)malloc(sizeof(struct BSTree_node));T->elem = elem;T->ltree = T->rtree = NULL;}else if(elem < T->elem);{T->ltree = insert_bstree(T->ltree, elem); //递归}else if(elem > T->elem);{T->rtree = insert_bstree(T->rtree, elem); //递归}else{printf("inserting repeat node is fobidden.\n");exit(0);}return T;
}//中序遍历
void in_order(struct BSTree_node *tree)
{if(tree){in_order(tree->ltree); //左printf("%d", tree->elem); //中in_order(tree->rtree); //右}
}//二叉搜索树查找
int search_bstree(struct BSTree_node *tree, unsigned int n)
{struct BSTree_node *p = tree; // 指针while(p){if(n == p->elem)return 1;else if(n < p->elem)p = p->ltree;elsep = p->rtree; }return 0;
}力扣题目
700. 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null
示例 1:

输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]示例 2:

输入:root = [4,2,7,1,3], val = 5
输出:[]
//c++
//递归1
class Solution {
public: //1.返回值参数TreeNode* searchBST(TreeNode* root, int val) {if (root == NULL || root->val == val) return root; // 2.终止条件TreeNode* result = NULL; // 变量存放返回值if (root->val > val) result = searchBST(root->left, val); // 3.单层搜索if (root->val < val) result = searchBST(root->right, val); // result 接住目标值指针return result; // 没有搜索到result就是NULL}
};
//递归2
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if (root == NULL || root->val == val) return root;if (root->val > val) return searchBST(root->left, val);if (root->val < val) return searchBST(root->right, val);return NULL;}
};//迭代法
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {while (root != NULL) { // 当节点不为空if (root->val > val) root = root->left; // > 左子树遍历else if (root->val < val) root = root->right; // < 右子树遍历else return root; // 等于时返回该节点}return NULL; // 如果搜索不到}
};701. 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:

输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
解释:另一个满足题目要求可以通过的树是:
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
//递归
class Solution {
private:TreeNode* parent;void traversal(TreeNode* cur, int val) { if (cur == NULL) { //2.终止条件,找到插入位置(叶子节点)TreeNode* node = new TreeNode(val);if (val > parent->val) parent->right = node;else parent->left = node;return;}parent = cur;if (cur->val > val) traversal(cur->left, val);if (cur->val < val) traversal(cur->right, val);return;}public:TreeNode* insertIntoBST(TreeNode* root, int val) {1.确定递归参数,返回值parent = new TreeNode(0);if (root == NULL) {root = new TreeNode(val);}traversal(root, val);return root;}
};//迭代
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if (root == NULL) {TreeNode* node = new TreeNode(val);return node;}TreeNode* cur = root;TreeNode* parent = root; // 这个很重要,需要记录上一个节点,否则无法赋值新节点while (cur != NULL) {parent = cur;if (cur->val > val) cur = cur->left;else cur = cur->right;}TreeNode* node = new TreeNode(val);if (val < parent->val) parent->left = node;// 此时是用parent节点的进行赋值else parent->right = node;return root;}
};-
删除二叉搜索树
#include <stdio.h>
#include <stdlib.h>
#define SIZE 10//二叉树节点
struct BSTree_node
{unsigned int elem;struct BSTree_node *ltree, *rtree; // 左右子树
};struct BSTree_node *create_bstree(unsigned int *pt, int n);
struct BSTree_node *insert_bstree(struct BSTree_node *T, unsigned int elem);
void in_order(struct BSTree_node *tree);
int search_bstree(struct BSTree_node *tree, unsigned int n);
struct BSTree_node *delete_bstree(struct BSTree_node *T, unsigned int elem);int main(void)
{unsigned int num;unsigned int arr[SIZE] = {37, 22, 11, 82, 67, 9, 45, 91, 33, 52}; // 无序数组struct BSTree_node *mytree = NULL;mytree = create_bstree(arr, SIZE); // 创建二叉树in_order(mytree); // 中序遍历printf("\n");
//查找printf("please enter a number you want to find in the BSTree:\n");scanf("%d", &num);if(search_bstree(mytree, num))printf("find %d in the mytree.\n", num);elseprintf("can't find %d in the mytree.\n", num);
//插入printf("please enter a number you want to insert in the BSTree:\n");scanf("%d", &num);mytree = insert_bstree(mytree, num);in_order(mytree);printf("\n");//删除printf("please enter a number you want to delet from the BSTree:\n");scanf("%d", &num);mytree = delete_bstree(mytree, num);in_order(mytree);printf("\n");return 0;
}// 创建二叉搜索树
struct BSTree_node *create_bstree(unsigned int *pt, int n)
{struct BSTree_node *tree = NULL;for(int i = 0; i < n; i++){tree = insert_bstree(tree, *pt);pt++;}return tree;
}
// 创建二叉搜索树插入节点
struct BSTree_node *insert_bstree(struct BSTree_node *T, unsigned int elem)
{if(!T){T = (struct BSTree_node *)malloc(sizeof(struct BSTree_node));T->elem = elem;T->ltree = T->rtree = NULL;}else if(elem < T->elem);{T->ltree = insert_bstree(T->ltree, elem); //递归}else if(elem > T->elem);{T->rtree = insert_bstree(T->rtree, elem); //递归}else{printf("inserting repeat node is fobidden.\n");exit(0);}return T;
}//中序遍历
void in_order(struct BSTree_node *tree)
{if(tree){in_order(tree->ltree); //左printf("%d", tree->elem); //中in_order(tree->rtree); //右}
}//二叉搜索树查找
int search_bstree(struct BSTree_node *tree, unsigned int n)
{struct BSTree_node *p = tree; // 指针while(p){if(n == p->elem)return 1;else if(n < p->elem)p = p->ltree;elsep = p->rtree; }return 0;
}//删除 使用后继点代替删除节点
struct BSTree_node *delete_bstree(struct BSTree_node *T, unsigned int elem)
{ //递归//1.空if(T == NULL){printf("no exist %d node.\n", elem);exit(0);}//2.等于时if(T->elem == elem){ //2.1 没有右子树,直接删除该节点,T指向左子树if(T->rtree == NULL){struct BSTree_node *temp = T; T = T->ltree;free(temp);}else //2.2 有右子树,找右子树最左点{struct BSTree_node *temp = T->rtree; while(temp->ltree) //找最左点temp = temp->ltree; T->elem = temp->elem;T->rtree = delete_bstree(T->rtree, T->elem); // 递归删除最左节点}}//3.大于或者小于时else if(T->elem > elem)T->ltree = delete_bstree(T->ltree, elem);elseT->rtree = delete_bstree(T->rtree, elem);return T;
}力扣题目
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。示例 1:

输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点示例 3:
输入: root = [], key = 0
输出: []确定单层递归的逻辑
这里就把二叉搜索树中删除节点遇到的情况都搞清楚。
有以下五种情况:
-
第一种情况:没找到删除的节点,遍历到空节点直接返回了
-
找到删除的节点
-
第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
-
第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
-
第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
-
第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
//递归
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (root == nullptr) return root; // 第一种情况:没找到删除的节点,遍历到空节点直接返回了if (root->val == key) {// 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点if (root->left == nullptr && root->right == nullptr) {///! 内存释放delete root;return nullptr;}// 第三种情况:其左孩子为空,右孩子不为空,删除节点,右孩子补位 ,返回右孩子为根节点else if (root->left == nullptr) {auto retNode = root->right;///! 内存释放delete root;return retNode;}// 第四种情况:其右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点else if (root->right == nullptr) {auto retNode = root->left;///! 内存释放delete root;return retNode;}// 第五种情况:左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置// 并返回删除节点右孩子为新的根节点。else {TreeNode* cur = root->right; // 找右子树最左面的节点while(cur->left != nullptr) {cur = cur->left;}cur->left = root->left; // 把要删除的节点(root)左子树放在cur的左孩子的位置TreeNode* tmp = root; // 把root节点保存一下,下面来删除root = root->right; // 返回旧root的右孩子作为新rootdelete tmp; // 释放节点内存(这里不写也可以,但C++最好手动释放一下吧)return root;}}if (root->val > key) root->left = deleteNode(root->left, key);if (root->val < key) root->right = deleteNode(root->right, key);return root;}
};//迭代
class Solution {
private:// 将目标节点(删除节点)的左子树放到 目标节点的右子树的最左面节点的左孩子位置上// 并返回目标节点右孩子为新的根节点// 是动画里模拟的过程TreeNode* deleteOneNode(TreeNode* target) {if (target == nullptr) return target;if (target->right == nullptr) return target->left;TreeNode* cur = target->right;while (cur->left) {cur = cur->left;}cur->left = target->left;return target->right;}
public:TreeNode* deleteNode(TreeNode* root, int key) {if (root == nullptr) return root;TreeNode* cur = root;TreeNode* pre = nullptr; // 记录cur的父节点,用来删除curwhile (cur) {if (cur->val == key) break;pre = cur;if (cur->val > key) cur = cur->left;else cur = cur->right;}if (pre == nullptr) { // 如果搜索树只有头结点return deleteOneNode(cur);}// pre 要知道是删左孩子还是右孩子if (pre->left && pre->left->val == key) {pre->left = deleteOneNode(cur);}if (pre->right && pre->right->val == key) {pre->right = deleteOneNode(cur);}return root;}
};530. 二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
示例 1:

输入:root = [4,2,6,1,3]
输出:1示例 2:

输入:root = [1,0,48,null,null,12,49]
输出:1501. 二叉搜索树中的众数
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树示例 1:

输入:root = [1,null,2,2]
输出:[2]示例 2:
输入:root = [0]
输出:[0]236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。示例 2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
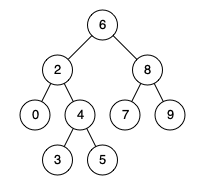
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点1 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。相关文章:

数据结构10 -查找_树表查找
创建二叉搜索树 二叉搜索树 二叉搜索树是有数值的了,二叉搜索树是一个有序树。 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它…...

第126天:内网安全-隧道技术SSHDNSICMPSMB上线通讯LinuxMac
知识点 #知识点: 1、入站规则不出网上线方案 2、出站规则不出网上线方案 3、隧道技术-SMB&ICMP&DNS&SSH 4、控制上线-Linux&Mac&IOS&Android-连接方向:正向&反向(基础课程有讲过) -内网穿透…...

开发一个饲料商城小程序需要多少钱
随着宠物行业的蓬勃发展,饲料商城小程序作为一个重要的销售渠道,吸引了越来越多的投资者。那么,开发一套饲料商城小程序需要多少钱呢?本文将为您详细解答。 首先,开发一套饲料商城小程序的价格受到多个因素的影响&…...

Emacs之set-face-attribute与font-lock-add-keywords用法区别(一百二十八)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

JavaScript高阶函数和闭包
在JavaScript编程中,高阶函数和闭包是两个重要而又常见的概念。它们是函数式编程的重要组成部分,可以让我们的代码更加灵活、简洁和高效。本文将详细解释高阶函数和闭包的概念、用法以及它们在JavaScript中的重要性。 高阶函数 1. 什么是高阶函数&…...

私有化部署企业IM即时通讯:提升效率、防止泄密、高效协同办公
随着科技的飞速发展和智能手机的普及,即时通讯(IM)应用在我们的生活和工作中变得越来越重要。在企业中,IM已成为员工之间交流沟通的主要方式之一。然而,对于大多数企业来说,选择私有化部署企业IM即时通讯软…...
react ant icon的简单使用
refer: 快速上手 - Ant Design 1.引入ant npm install antd --save 2.在页面引用: import { StarOutlined } from ant-design/icons; 如果想要引入多个icon,可以这样书写: import { UserOutlined, MailOutlined, PieChartOutlined } fr…...

用Rust实现23种设计模式之原型模式
在 Rust 中,原型模式可以通过实现 Clone trait 来实现。原型模式是一种创建型设计模式,它允许通过复制现有对象来创建新对象,而无需显式地使用构造函数。下面是一个使用 Rust 实现原型模式的示例,带有详细的代码注释和说明&#x…...

visual studio 2022 编译时出现MSB3721问题
cuda1C:\code\SSR\Impl\Dev\gE\cO\G.Common.XrayRegistration_nc>“C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v11.7\bin\nvcc.exe” -gencodearchcompute_86,code“sm_86,compute_86” --use-local-env -ccbin “C:\Program Files\Microsoft Visual Studio\2022…...
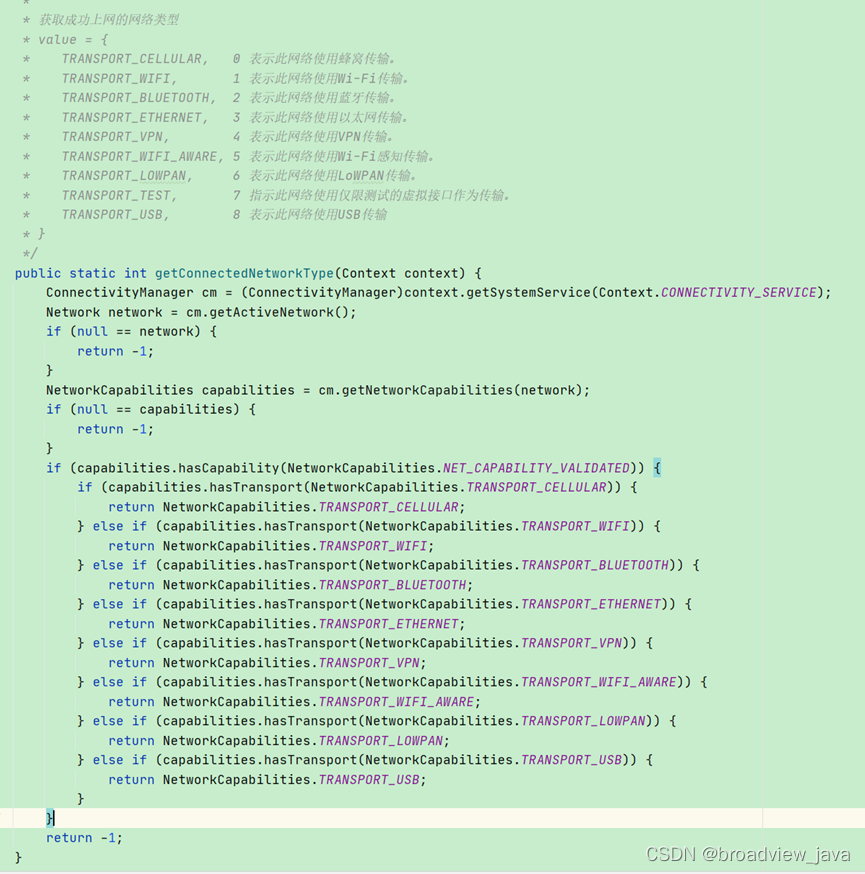
Android 获取网络连接状态新方法
一. 问题背景 Android12上,有的app模块判断当前网络的类型和连接状态时,还是使用的旧的API,导致返回的结果不准确,影响代码逻辑判断,本篇文章就这一问题,整理一下判断网络类型和连接状态的新方法。 二. 原因…...
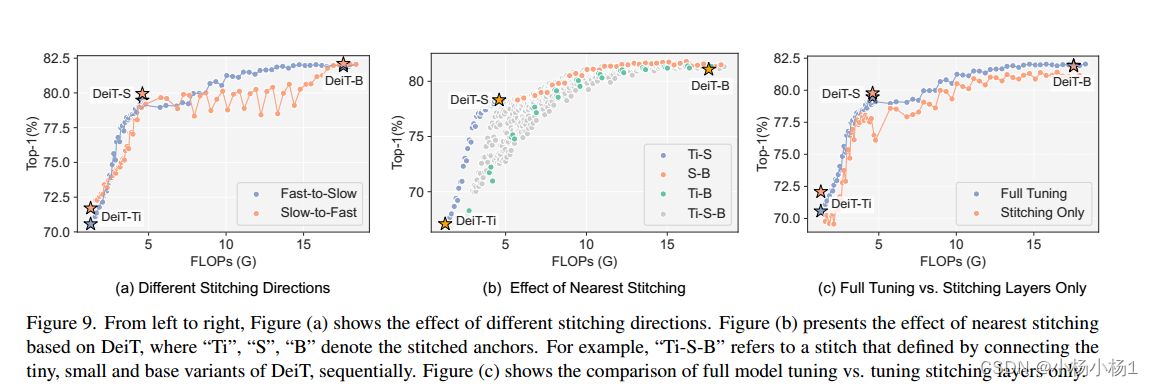
可缝合神经网络
文章目录 Stitchable Neural Networks摘要本文方法实验结果 Stitchable Neural Networks 摘要 包含大量强大的预训练模型族(如ResNet/DeiT)的model zoo已经达到了前所未有的范围,这对深度学习的成功有重要贡献。由于每个模型族都由具有不同尺度的预训练模型(例如&…...
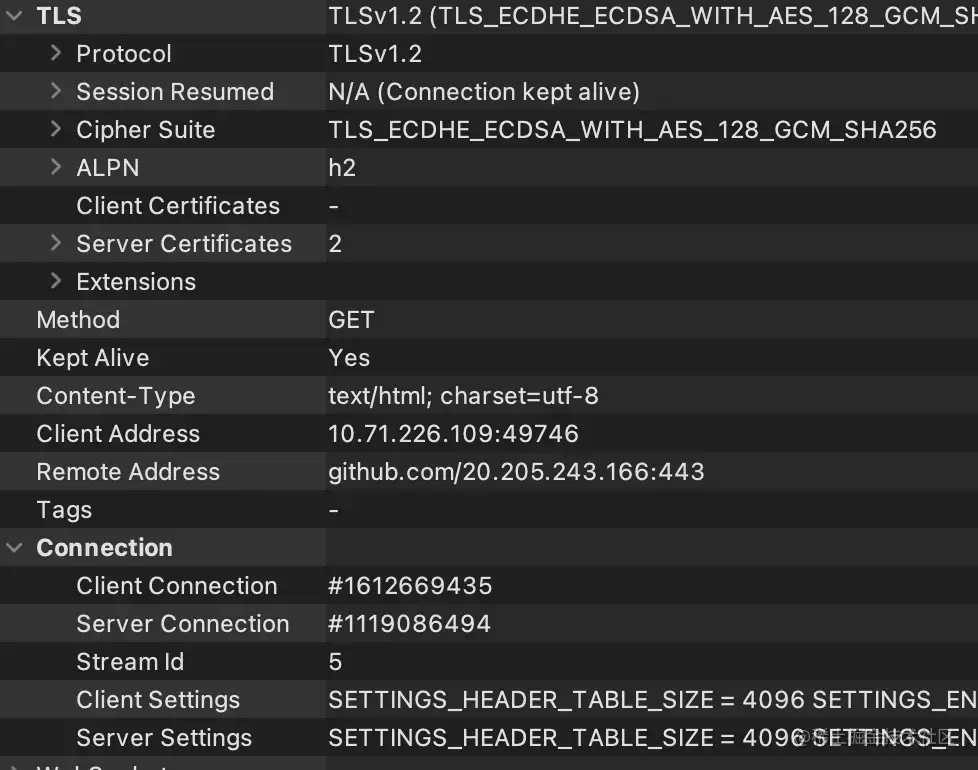
Android优化篇|网络预连接
作者:苍耳叔叔 一个示例 前后分别去请求同一个域名下的接口,通过 Charles 抓包,可以看到 Timing 下面的时间: 第二次请求时,DNS、Connect 和 TLS Handshake 部分都是 -,说明没有这部分的耗时,…...
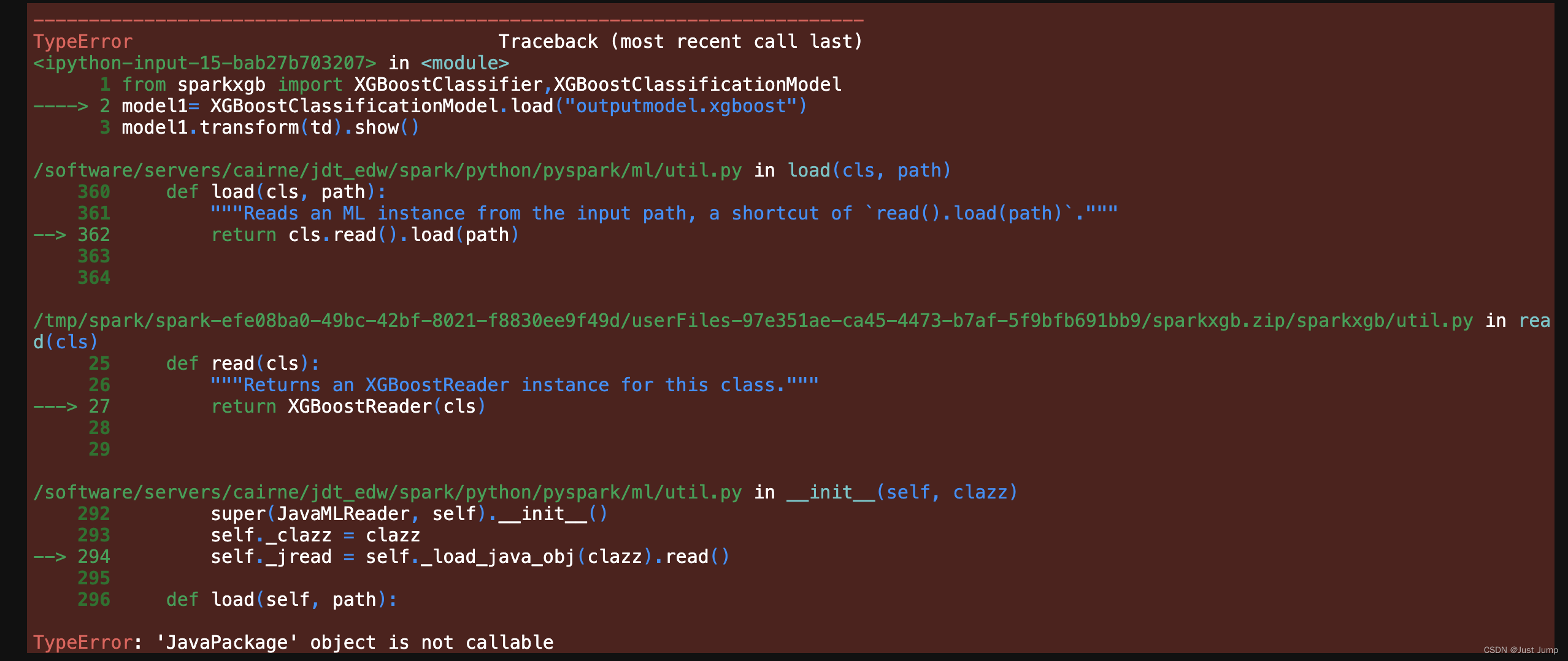
pyspark使用XGboost训练模型实例
遇到一个还不错的使用Xgboost训练模型的githubhttps://github.com/MachineLP/Spark-/tree/master/pyspark-xgboost 1、这是一个跑通的代码实例,使用的是泰坦尼克生还数据,分类模型。 这里使用了Pipeline来封装特征处理和模型训练步骤,保存为…...
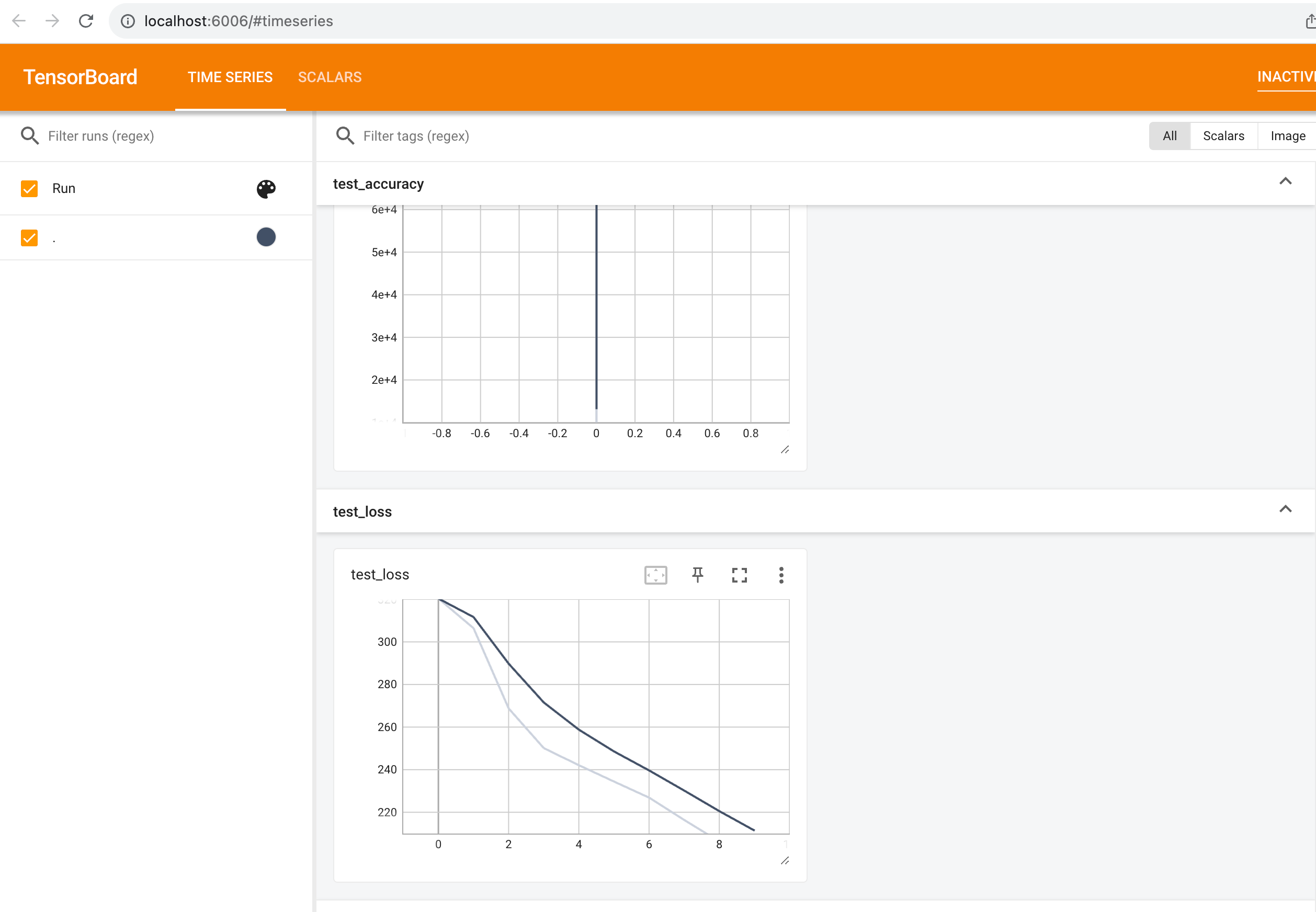
完整模型的训练套路
从心所欲 不逾矩 天大地大 皆可去 一、官方模型的初使用 使用VGG16模型 VGG模型使用代码示例: import torchvision.models from torch import nndataset torchvision.datasets.CIFAR10(/cifar10, False, transformtorchvision.transforms.ToTensor())vgg16_true …...

PtahDAO:全球首个DAO治理资产信托计划的金融平台
金融科技是当今世界最具创新力和影响力的领域之一,区块链技术作为金融科技的核心驱动力,正在颠覆传统的金融模式,为全球用户提供更加普惠、便捷、安全的金融服务。在这个变革的浪潮中,PtahDAO(普塔道)作为全…...
从零搭建一个react + electron项目
最近打算搭建一个react electron的项目,发现并不是那么傻瓜式 于是记录一下自己的实践步骤 通过create-react-app 创建react项目 npx create-react-app my-app 安装electron依赖 npm i electron -D暴露react项目的配置文件(这一步看自己需求,…...

MATLAB /Simulink 快速开发STM32(使用st官方工具 STM32-MAT/TARGET),以及开发过程
配置好环境以后就是开发: stm32cube配置芯片,打开matlab添加ioc文件,写处理逻辑,生成代码,下载到板子中去。 配置需要注意事项: STM32CUBEMAX6.5.0 MABLAB2022BkeilV5.2 Matlab生成的代码CTRLB 其中关键的…...
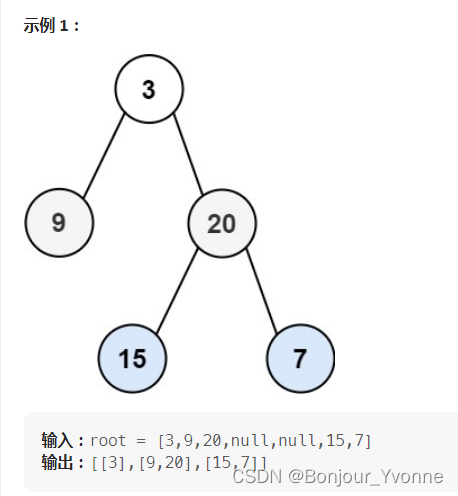
LeetCode 热题 100 JavaScript--102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 输入:root [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]] 示例 2: 输入:root [1…...

常见Git命令
Git常见命令 1. 添加单个文件 git add a.txt2. 添加多个文件 git add a.txt b.txt c.txt3. 添加(commit)修改,此时修改还未push到服务器上 git commit -m "修改了a.txt内容"4. 提交(push)修改,此时修改会同步到服务器上 git push5. 查看当…...

在C语言中调用汇编语言的函数
在C语言中调用汇编文件中的函数,要做的主要工作有两个: 一是在C语言中声明函数原型,并加extern关键字; 二是在汇编中用EXPORT导出函数名,并用该函数名作为汇编代码段的标识,最后用mov pc, lr返回。然后&a…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
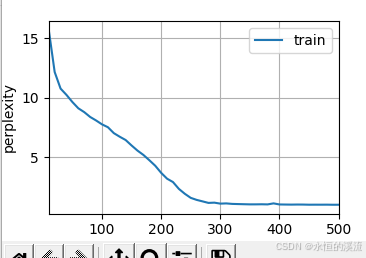
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...
