算法提高-树状数组
算法提高-树状数组
- 241. 楼兰图腾(区间求和 + 单点修改)
- 242. 一个简单的整数问题(差分+推公式 实现 维护区间修改+单点求和)
- 243. 一个简单的整数问题2(区间修改和区间求和)
- AcWing 244. 谜一样的牛(用二分查找想要的状态 + 树状数组动态记录当前区间的状态)
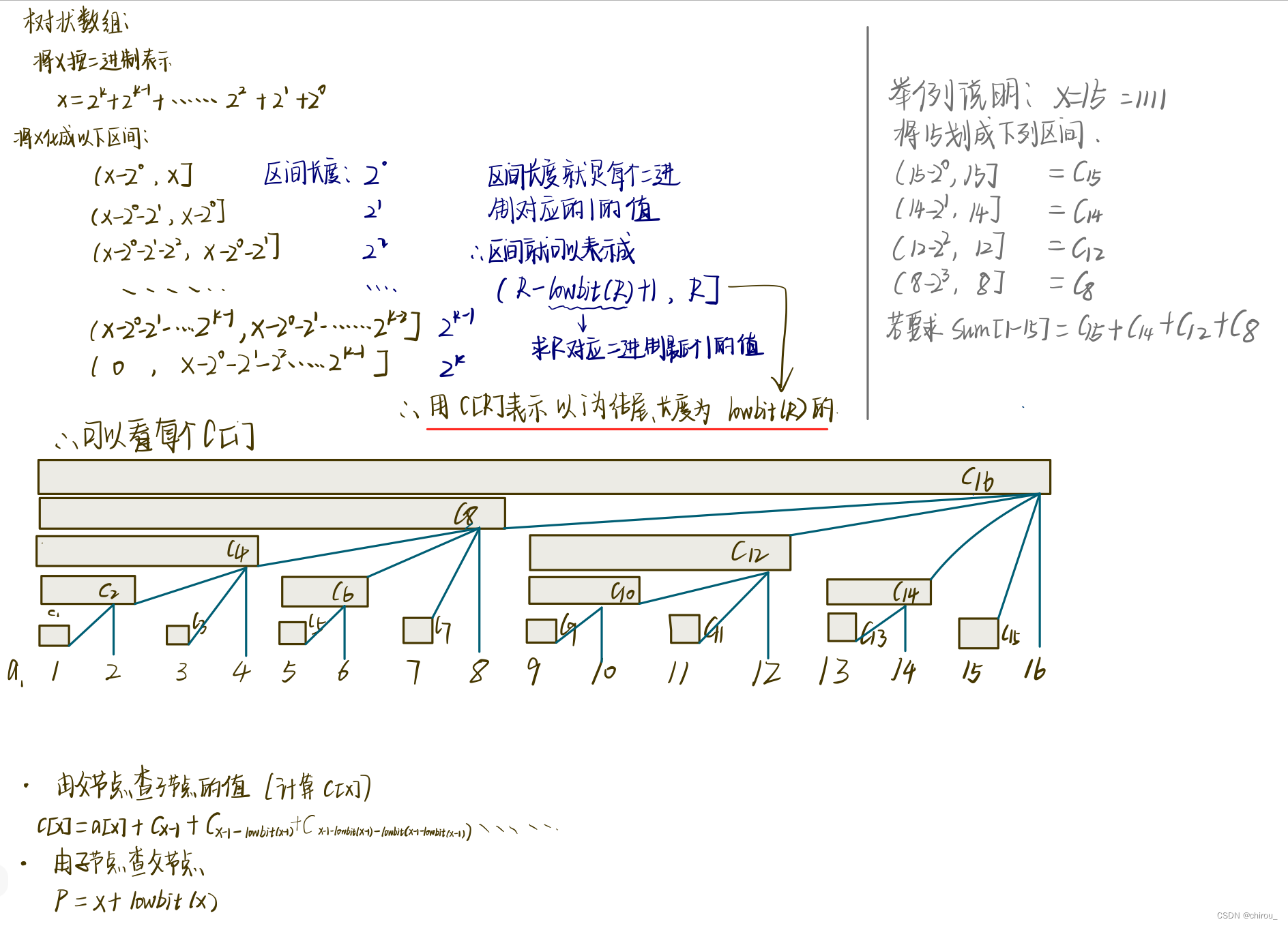
树状数组的两个作用
- 快速求区间和
- 快速修改某一个数同时可以快速修改区间和
- tr[i]记录的区间的长度是lowbit(i)
241. 楼兰图腾(区间求和 + 单点修改)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
typedef pair<int, int> pii;
const int N = 2e5 + 10;
int tr[N];
int a[N];
int n;
int lowbit(int x)
{return x & -x;
}
void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}int sum(int x)//统计下标为1-x的前缀和
{int res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res;
}void solve()
{scanf("%d", &n);vector<int> Greater(N+1);//y的取值正好也是1-n,否则就需要离散化了vector<int> lower(N+1);for (int i = 1; i <= n; ++ i) scanf("%d", &a[i]);for (int i = 1; i <= n; ++ i){int y = a[i];Greater[i] = sum(n) - sum(y);//遍历到a[i]的时候,下标为(1, n)在n~y+1之间的数有几个lower[i] = sum(y-1);遍历到a[i]的时候,从1~y-1之间的数有几个add(y, 1);//遍历完a[i]后,将a[i]出现的次数加1,我们前缀和sum}memset(tr, 0, sizeof tr);typedef long long LL;LL res1 = 0, res2 = 0;for (int i = n; i; -- i)//逆向遍历{res1 += Greater[i] *(LL)(sum(n) - sum(a[i]));//记录下标在(n, i)之间有多少个数字大于a[i]res2 += lower[i] * (LL)(sum(a[i]-1));add(a[i], 1);}cout << res1 << " "<< res2;
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;// cin >> T;while (T --) solve();return 0;
}
242. 一个简单的整数问题(差分+推公式 实现 维护区间修改+单点求和)
树状数组擅长的是单点加然后求区间和,本题是区间加然后求单点和;
- 在原数组上求某个点的值 = 求差分数组的前缀和
- 在原数组上更改某个区间的值 = 修改差分数组两个端点的值
为了将我们对原数组的操作转化为经典的树状数组的操作(修改单点的值, 求一个区间的和),我们这里tr[]维护的就是a[]的差分数组。
差分数组b[]和原数组a[]的关系
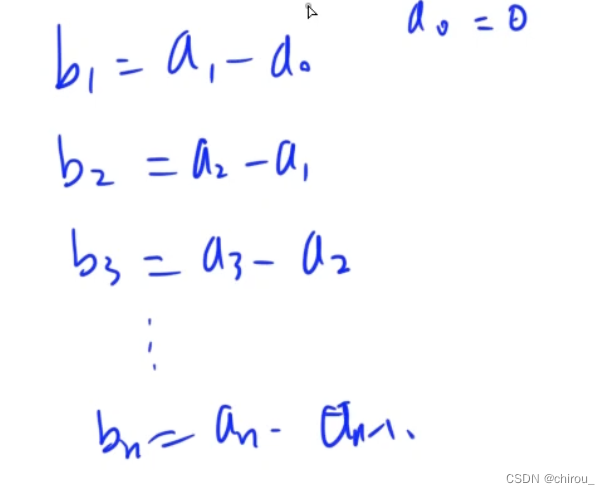
用树状数组实现前缀和 脱裤子放屁多此一举版本
事实上能写出这种代码还是没有理解树状数组的作用是啥,树状数组的作用就是区间求和和单点修改,使得区间求和和单点修改的复杂度都不至于太慢。
数组的区间求和复杂度是n,单点修改复杂度是1
前缀和的区间求和复杂度是1,单点修改的复杂度是n;
树状数组的区间求和和单点修改的复杂度都是logn。
本题是区间修改和单点求和,这显然不是树状数组的正常操作,即我们树状数组不能去维护a[],而是应该去维护他的差分数组b[]
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
typedef long long LL;
int a[N];
LL tr[N];
int n, m;
// 10 5
// 1 2 3 4 5 6 7 8 9 10
// Q 4
// Q 1
// Q 2
// C 1 6 3
// Q 2
int lowbit(int x)
{return x & -x;
}
void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
LL presum(int x)
{LL res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res ;
}
void solve()
{cin >> n >> m;for (int i = 1; i <= n; ++ i) {cin >> a[i];add(i, a[i]);}char op[2];while (m -- ){cin >> op;int l, r, x;if (*op == 'Q'){cin >> x;cout << presum(x) - presum(x - 1)<< endl;//这不就是前缀和么,虽然查找是1,但是修改就很大了,} //我用树状数组多次一举的话更大else {cin >> l >> r >> x;for(int i = l; i <= r; ++ i)//可以看到前缀和的话修改操作的复杂度是n^2logn{add(i, x);}}}}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;// cin >> T;while (T --) solve();return 0;
}
ac代码
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
typedef long long LL;
int a[N];
LL tr[N];
int n, m;
// 10 5
// 1 2 3 4 5 6 7 8 9 10
// Q 4
// Q 1
// Q 2
// C 1 6 3
// Q 2
int lowbit(int x)
{return x & -x;
}
void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
LL presum(int x)
{LL res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res ;
}
void solve()
{cin >> n >> m;for (int i = 1; i <= n; ++ i) {cin >> a[i];add(i, a[i] - a[i - 1]);}char op[2];while (m -- ){cin >> op;int l, r, x;if (*op == 'Q'){cin >> x;cout << presum(x) << endl;//这不就是前缀和么,虽然查找是1,但是修改就很大了,} //我用树状数组多次一举的话更大else {cin >> l >> r >> x;add(l, x);add(r + 1, -x);}}}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;// cin >> T;while (T --) solve();return 0;
}
243. 一个简单的整数问题2(区间修改和区间求和)
- 区间求和 + 单点修改 = 普通树状数组(对前缀和以及普通数组的优化)
- 区间修改 + 单点求和 = 树状数组维护差分数组(这样的话区间修改就可以对应到单点修改差分数组,单点求和就可以对应到区间求差分数组的和)
- 区间求和 + 区间修改 = 维护两个树状数组,一个用维护差分数组b[i](可以做到区间修改),一个维护i*b[i],推公式可以得出对a[]数组区间求和就是下面这个公式

还不懂的话可以看下面这段解释


因为多维护一个i * b[i], add函数里面的c可能会爆int,所以要强转一下
经验:
- 如果过了样例数据也过了大部分,那就看一下是不是没开longlong
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
typedef long long LL;
int a[N];
LL tr[N], tri[N];
int n, m;int lowbit(int x)
{return x & -x;
}
void add(LL tree[], int x, LL c)//开LL
{for (int i = x; i <= n; i += lowbit(i)) tree[i] += c;
}
LL presum(LL tree[], int x)
{LL res = 0;for (int i = x; i; i -= lowbit(i)) res += tree[i];return res ;
}
LL prefixsum (int x)
{return presum(tr, x) * (x + 1) - presum(tri, x);
}
void solve()
{cin >> n >> m;for (int i = 1; i <= n; ++ i) {cin >> a[i];add(tr, i, a[i] - a[i - 1]);add(tri, i, (LL)i * (a[i] - a[i - 1]));//开LL}char op[2];while (m -- ){cin >> op;int l, r, x;if (*op == 'Q'){cin >> l >> r;cout << prefixsum(r) - prefixsum(l - 1) << endl;}else {cin >> l >> r >> x;add(tr, l, x); add(tr, r + 1, -x);add(tri, l, l * x); add(tri, r + 1, (r + 1) * (-x));}}}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;// cin >> T;while (T --) solve();return 0;
}
AcWing 244. 谜一样的牛(用二分查找想要的状态 + 树状数组动态记录当前区间的状态)
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
int tr[N], pos[N];
int n;
// 5
// 1
// 2
// 1
// 0
int lowbit(int x)
{return x & -x;
}
void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
int presum(int x)//树状数组的本质就是求前缀和
{int sum = 0;for (int i = x; i; i -= lowbit(i)) sum += tr[i];return sum;
}
int find(int k)//
{int l = 1, r = n;while (l < r){int mid = l + r >> 1;if (presum(mid) >= k) r = mid;//求高度为1到n之间高度为mid的牛之前有多少头牛还没有被用过,其实也就是求高度为mid的牛在当前剩下的牛中是否为第k高的牛else l = mid + 1; //因为我们求的是第一个第k高的牛,那么当前搜索的高度为mid的牛一定是还没有确定位置的牛}return l;
}
void solve()
{cin >> n;add(1, 1);for (int i = 2; i <= n; ++ i){cin >> pos[i];add(i, 1);//单点修改tr[i] = 1,同时对i后面的树状数组造成影响。树状数组的本质就是前缀和,同时单点修改的复杂度也不低不高}vector<int> ans(n + 1);for (int i = n; i; -- i){int height;height = find(pos[i] + 1);//找到当前在剩下的牛中第pos + i高的牛,它的高度是heightans[i] = height;add(height, -1);//表明这个height这个高度的牛已经用过了,他会对1-n中高度 >height的牛的前缀和造成影响}for (int i = 1; i <= n; ++ i) cout << ans[i] << endl;
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;// cin >> T;while (T --) solve();return 0;
}相关文章:

算法提高-树状数组
算法提高-树状数组 241. 楼兰图腾(区间求和 单点修改)242. 一个简单的整数问题(差分推公式 实现 维护区间修改单点求和)243. 一个简单的整数问题2(区间修改和区间求和)AcWing 244. 谜一样的牛(…...

Django ORM详解:最全面的数据库处理指南
概要 深度探讨Django ORM的概念、基础使用、进阶操作以及详细解析在实际使用中如何处理数据库操作。这篇文章旨在帮助大家全面掌握Django ORM,理解其如何简化数据库操作,并透过表象理解其内部工作原理。 Django ORM简介 在深入讨论Django的ORMÿ…...

Istio 安全 授权管理AuthorizationPolicy
这个和cka考试里面的网络策略是类似的。它是可以实现更加细颗粒度限制的。 本质其实就是设置谁可以访问,谁不可以访问。默认命名空间是没有AuthorizationPolicy---允许所有的客户端访问。 这里是没有指定应用到谁上面去,有没有指定使用哪些客户端&#…...
04 Ubuntu中的中文输入法的安装
在Ubuntu22.04这种版本相对较高的系统中安装中文输入法,一般推荐使用fctix5,相比于其他的输入法,这款输入法的推荐词要好得多,而且不会像ibus一样莫名其妙地失灵。 首先感谢文章《滑动验证页面》,我是根据这篇文章的教…...
faac内存开销较大,为方便嵌入式设备使用进行优化(valgrind使用)
faac内存开销较大,为方便嵌入式设备使用进行优化,在github上提了issues但是没人理我,所以就搞一份代码自己玩吧。 基于faac_1_30版本,原工程https://github.com/knik0/faac faac内存优化: faac内存开销较大,为方便嵌入…...
)
分数线划定(c++题解)
题目描述 世博会志愿者的选拔工作正在 A 市如火如荼的进行。为了选拔最合适的人才,A 市对所有报名的选手进行了笔试,笔试分数达到面试分数线的选手方可进入面试。面试分数线根据计划录取人数的 150% 划定,即如果计划录取 m 名志愿者…...
React 在 html 中 CDN 引入(包含 antd、axios ....)
一、简介 cdn 获取推荐 https://unpkg.com,unpkg 是一个快速的全球内容交付网络,适用于 npm 上所有内容。 【必备】react 相关 cdn。附:github 官方文档获取、现阶段官方文档 CDN 网址。 <script crossorigin src"https://unpkg.com…...

数据结构----异或
数据结构----异或 一.何处用到了异或 1. 运算符 //判断是否相同 用到了异或,看异或结果如果是0就是相同,不是0就是不同//注意: 不能给小数用,小数没有相等的概念,所以小数判断是否相同都是进行相减判断2.找一堆数中…...

PHP Smarty模板的语法规则是怎样的?
首先,你要知道Smarty模板是以模板格式来编写的。模板格式类似于HTML,但它的语法更加简洁明了。 以下是PHP Smarty模板的语法规则和代码例子: 变量:在Smarty模板中,你可以使用变量来显示动态内容。变量通常以“{$”符…...

Socks IP轮换:为什么是数据挖掘和Web爬取的最佳选择?
在数据挖掘和Web爬取的过程中,IP轮换是一个非常重要的概念。数据挖掘和Web爬取需要从多个网站或来源获取数据,而这些网站通常会对来自同一IP地址的请求进行限制或封锁。为了避免这些问题,数据挖掘和Web爬取过程中需要使用Socks IP轮换技术。在…...

优化|当机器学习上运筹学:PyEPO与端对端预测后优化
分享者:唐博 编者按: 这篇文章我想要写已经很久了,毕竟“端对端预测后优化”(End-to-End Predict-then-Optimize)正是我读博期间的主要研究方向,但我又一直迟迟没能下笔。想说自己杂事缠身(实…...
Cocos Creator的 Cannot read property ‘applyForce‘ of undefined报错
序: 1、博主是看了这个教程操作的时候出的bug>游戏开发 | 17节课学会如何用Cocos Creator制作3D跑酷游戏 | P9 代码控制对象移动_哔哩哔哩_bilibili 2、其实问题不是出在代码上,但是发现物体就是不平移 3、node全栈的资料》node全栈框架 正文…...

纯css实现九宫格图片
本篇文章所分享的内容主要涉及到结构伪类选择器,不熟悉的小伙伴可以了解一下,在常用的css选择器中我也有分享相关内容。 话不多说,接下来我们直接上代码: <!DOCTYPE html> <html lang"en"><head>&l…...

【MySQL】数据库的增删查改+备份与恢复
文章目录 一、创建数据库create二、数据库所使用的编码2.1 查询字符集和校验集2.2 指定编码创建数据库2.3 不同的校验集对比 三、删除数据库drop四、查看数据库show五、修改数据库alter六、数据库的备份与恢复6.1 备份 mysqldump6.2 恢复source6.3 仅备份几张表或备份多个数据库…...

Docker 部署 redis 举例
1、搜索镜像,也可以访问 https://hub.docker.com/ 搜索镜像,查看所有版本。 $ docker search redis2、拉取镜像 $ docker pull redis:5.03、启动镜像,并配置相关映射与绑定(附:Docker 常用命令与指令参数)…...

通过HandlerMethodArgumentResolver实现统一添加接口入参参数
背景:项目中有些接口的入参需要用户id信息,最简单的做法在每个Controller方法调用的时候获取登录信息然后给入参设置用户id,但是这样就会有很多重复性的工作。另一个可行的也更好的方案可以使用HandlerMethodArgumentResolver来实现。 部分示…...

JAVA-spring boot 2.4.X报错Unable to find GatewayFilterFactory with name Hystrix
网关升级spring boot项目后,启动网关报错,具体报错信息如下: 2021-12-06 09:06:25.335 ERROR 45102 --- [oundedElastic-3] reactor.core.publisher.Operators : Operator called default onErrorDropped reactor.core.Exceptions$ErrorCallback…...

运输层---UDP协议
目录 一. 无连接运输:UDP1.1 定义1.2 特点1.3 应用 二. UDP报文段结构三. UDP检验和3.1 定义3.2 检验和计算实例3.2 UDP检验和的局限 一. 无连接运输:UDP 1.1 定义 UDP(User Datagram Protocol)用户数据报协议:由 [RF…...
【LeetCode】剑指 Offer Ⅱ 第3章:字符串(7道题) -- Java Version
题库链接:https://leetcode.cn/problem-list/e8X3pBZi/ 题目解决方案剑指 Offer II 014. 字符串中的变位词双指针 数组模拟哈希表 ⭐剑指 Offer II 015. 找到字符串中所有字母异位词双指针 数组模拟哈希表 ⭐剑指 Offer II 016. 不含重复字符的最长子字符串双指针…...
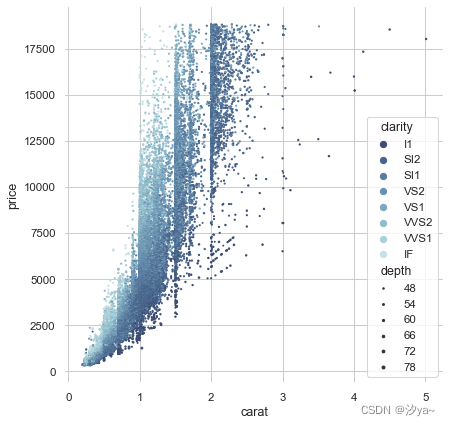
【python】绘图代码模板
【python】绘图代码模板 pandas.DataFrame.plot( )画图函数Seaborn绘图 -数据可视化必备主题样式导入数据集可视化统计关系散点图抖动图箱线图小提琴图Pointplot群图 可视化数据集的分布绘制单变量分布柱状图直方图 绘制双变量分布Hex图KDE 图可视化数据集中的成对关系 好看的图…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...
