规划模型Matlab代码
文章目录
- 数学规划定义
- 一般形式
- 分类
- 1.线性规划(linear programming)
- 2.非线性规划(nonlinear programming)
- 3. 整数规划(integer programming)
- 4. 0-1规划(0-1 programming)
- 5. 最大最小化模型
- 6. 多目标规划模型
- 7.敏感性分析(对权重)
- [例题]
数学规划定义
数学规划是统筹学的一个分支,用来研究:在给定条件下(约束条件),如何按照某一行衡量指标(目标函数)来寻求计划、管理工作中的最优方案。
通俗的讲,就是求目标函数在一定约束条件下的极值问题。
一般形式
min(或max):z = f(x)
x:决策变量(一般有多个自变量)
f(x):目标函数
不等式约束、等式约束、整数约束:约束条件
分类
线性规划
非线性规划
整数规划
0-1规划
1.线性规划(linear programming)
目标函数f(x)和约束条件均是决策变量的线性表达式。

注:linprog函数 只能求解最小值问题,最大值问题要在目标函数前加负号,转化为最小值问题,将结果 fval = - fval 即可。
2.非线性规划(nonlinear programming)
目标函数f(x) 和 约束条件中存在决策变量的非线性表达式。
注:解决起来比线性规划困难,目前没有通用的算法,大多数算法都是在选定决策变量的初始之后通过一定的收索方法寻求最优的决策变量。

3. 整数规划(integer programming)
存在变量要求取整数值的数学规则,分为 线性整数规划 和 非线性整数规划 。
注:目前所流行的求解整数规划的算法往往只适用于线性整数规划。
[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
% Matlab线性整数规划求解
% intcon 参数可以指定哪些决策变量是整数(行向量)。
0-1规划(0-1 programming)
4. 0-1规划(0-1 programming)
整数规划的特例,整数变量的取值只能为0和1。
[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
% 仍然使用线性整数规划的 intlinprog 函数,只不过在lb和ub上做文章。
% 0-1变量的 lb = 0, ub = 1。
5. 最大最小化模型
在最不利的的条件下,寻求最有利的策略。
[x,feval] = fminimax(@Fun,x0,A,b,Aeg,beg,lb,ub,@nonlfun,option)
max(feval)
% 目标函数 Fun 用一个函数向量表示
% 其他变量与非线性规划相同
6. 多目标规划模型
一个规划问题中有多个目标。
解决方案:对多目标函数进行加权组合将问题变为单目标规划。
[x fval] = linprog(c, A, b, Aeq, beq, lb,ub, x0)
% 仍然使用线性规划的 linprog 函数
% c中系数乘上了相应权重,并除以某一个常数(做标准化)
注:
多个目标函数统一为最大化或最小化问题后才可以进行加权组合。
如果目标函数量纲不相同,则需要对其进行标准化后再进行加权。标准化的方法一般是由目标函数除以某一个常数,该常数是指目标函数某个取值具体取值可根据经验确定。
对多目标函数进行加权求和时,权重需要由该问题领域的专家给定。实际建模比赛中若无特殊要求我们可另权重相同。
7.敏感性分析(对权重)
通过逐一改变相关变量数值的方法来解释关键指标受这些因素变动影响大小规律。
[例题]
某化工厂今年拟生产两种新产品 A 和 B,其生产费用分别为 2 万元/吨和 5 万元/吨。这两种产品均将造成环境污染,每生产一吨 A 产品会产生 0.4 吨的污染,每生产一吨 B产品会产生 0.3 吨的污染。由于条件限制,工厂生产产品A和B的最大生产能力各为每月5吨和 6 吨,而市场需要这两种产品的总量每月不少于7 吨。该工厂决策认为,这两个目标中环境污染应优先考虑,且根据经验生产费用的参考值为 30 万元,污染量参老缜园试问工厂如何安排生产计划,在满足市场需要的前提下,使设备的花费和产生的污染均达最小。
%% 多目标规划
w1 = 0.4; w2 = 0.6; % 两个目标函数的权重 x1 = 5 x2 = 2
% w1 = 0.5; w2 = 0.5; % 两个目标函数的权重 x1 = 5 x2 = 2
% w1 = 0.3; w2 = 0.7; % 两个目标函数的权重 x1 = 1 x2 = 6
c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3]; % 线性规划目标函数的系数
A = [-1 -1]; b = -7; % 不等式约束
lb = [0 0]'; ub = [5 6]'; % 上下界
[x,fval] = linprog(c,A,b,[],[],lb,ub) % 求解线性规划时使用 —— 目标函数和约束条件都是线性的
f1 = 2*x(1)+5*x(2)
f2 = 0.4*x(1) + 0.3*x(2)%% 敏感性分析
clear;clc
W1 = 0.1:0.001:0.5; W2 = 1- W1;
n =length(W1);
F1 = zeros(n,1); F2 = zeros(n,1); X1 = zeros(n,1); X2 = zeros(n,1); FVAL = zeros(n,1);
A = [-1 -1]; b = -7; % 不等式约束
lb = [0 0]; ub = [5 6]; % 上下界
for i = 1:nw1 = W1(i); w2 = W2(i);c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3]; % 线性规划目标函数的系数[x,fval] = linprog(c,A,b,[],[],lb,ub);F1(i) = 2*x(1)+5*x(2);F2(i) = 0.4*x(1) + 0.3*x(2);X1(i) = x(1);X2(i) = x(2);FVAL(i) = fval;
end% 「Matlab」“LaTex字符汇总”讲解:https://blog.csdn.net/Robot_Starscream/article/details/89386748
% 在图上可以加上数据游标,按住Alt加鼠标左键可以设置多个数据游标出来。
figure(1)
plot(W1,F1,W1,F2)
xlabel('f_{1}的权重')
ylabel('f_{1}和f_{2}的取值')
legend('f_{1}','f_{2}')figure(2)
plot(W1,X1,W1,X2)
xlabel('f_{1}的权重')
ylabel('x_{1}和x_{2}的取值')
legend('x_{1}','x_{2}')figure(3)
plot(W1,FVAL) % 看起来是两个直线组合起来的下半部分
xlabel('f_{1}的权重')
ylabel('综合指标的值')
相关文章:

规划模型Matlab代码
文章目录 数学规划定义一般形式分类 1.线性规划(linear programming)2.非线性规划(nonlinear programming)3. 整数规划(integer programming)4. 0-1规划(0-1 programming)5. 最大最小化模型6. 多目标规划模型7.敏感性分析(对权重)[例题] 数学规划定义 数…...

用html+javascript打造公文一键排版系统11:改进单一附件说明排版
一、用htmljavascript打造公文一键排版系统10中的一个bug 在 用htmljavascript打造公文一键排版系统10:单一附件说明排版 中,我们对附件说明的排版函数是: function setAtttDescFmt(p) {var t p;var a ;if (-1 ! t.indexOf(:))//是半角冒…...

snap xxx has “install-snap“ change in progress
error description * 系重复安装,进程冲突 solution 展示snap的改变 然后sudo snap abort 22即可终止该进程 之后重新运行install command~~ PS: ubuntu有时候加载不出来,执行resolvectl flush-caches,清除dns缓存…...

Elasticsearch 性能调优指南
目录 1、通用优化策略 1.1 通用最小化法则 1.2 职责单一原则 1.3 其他 2、写性能调优 2.1 基本原则 2.2 优化手段 2.2.1 增加 flush 时间间隔, 2.2.2 增加refresh_interval的参数值 2.2.3 增加Buffer大小, 2.2.4 关闭副本 2.2.5 禁用swap 2…...

学习Boost一:学习方法和学习目的
学习目的 Boost 的学习目的: 因为从知乎和CSND上根据了解内容来看,Boost作为一个历史悠久的开源库,已经脱离了一个单纯的库的概念了,他因庞大的涉及面应当被称之为库集。 并且,因为boost库优秀的试用反馈和开发人员的…...

c语言每日一练(1)
前言: 每日一练系列,每一期都包含5道选择题,2道编程题,博主会尽可能详细地进行讲解,令初学者也能听的清晰。每日一练系列会持续更新,暑假时三天之内必有一更,到了开学之后,将看学业情…...

iOS开发-CocoaLumberjack日志库实现Logger日志功能
iOS开发-Logger日志功能实现 在iOS开发中,常用CocoaLumberjack来作为日志功能实现的日志框架 一、CocoaLumberjack是什么? CocoaLumberjack 是 支持 iOS 和 Mac 平台的日志框架,使用简单,功能强大且不失灵活,它的主…...
深度学习(34)—— StarGAN(2)
深度学习(34)—— StarGAN(2) 完整项目在这里:欢迎造访 文章目录 深度学习(34)—— StarGAN(2)1. build model(1)generator(2&#…...

use lua
-- basic.lua print("hello ".."world") local a 1 --only this file can see b 2 -- global see -- not declare vaiable all asign to nil print(fuck) -- 字符串可以"" , ,[[]] -- 一些数值运算支持,进制数,科学数&a…...
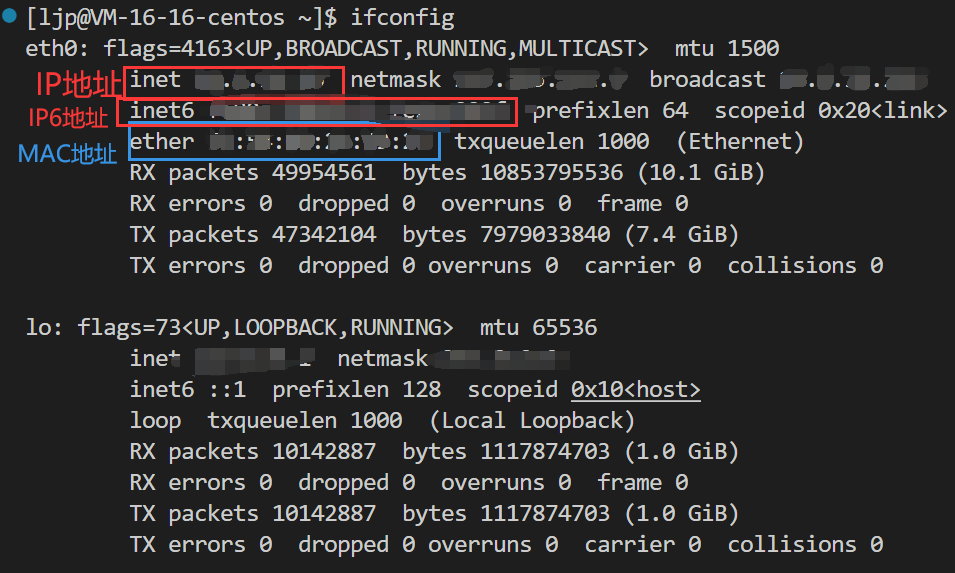
网络——初识网络
网络基础 文章目录 网络基础计算机网络产生的背景认识网络协议网络协议初识协议分层OSI七层模型TCP/IP四层模型网络传输基本流程协议报头 认识IP地址认识MAC地址ifconfig查看主机地址ifconfig查看主机地址 计算机网络产生的背景 独立模式:计算机之间相互独立 早期的…...

调试技巧(2)
6. 如何写出好(易于调试)的代码 6.1 优秀的代码: 代码运行正常bug很少效率高可读性高可维护性高注释清晰文档齐全 常见的coding技巧: 使用assert尽量使用const养成良好的编码风格添加必要的注释避免编码的陷阱。 这里讲一下assert…...

骨传导耳机真不伤耳吗?骨传导耳机有什么好处?
骨传导耳机真不伤耳吗?骨传导耳机有什么好处? 我先来说说骨传导耳机的工作原理吧,骨传导是一种传声方式,声波通过颅骨、颌骨等头部骨头的振动,将声音传到内耳。其实骨传导的现象我们很常见,就像我们平时嗑瓜…...

mac切换jdk版本
查询mac已有版本 1、打开终端,输入: /usr/libexec/java_home -V注意:输入命令参数区分大小写(必须是-V) 2.目前本地装有两个版本的jdk xxxxedydeMacBook-Pro-9 ~ % /usr/libexec/java_home -V Matching Java Virtual Machines (2):20.0.1 (…...
go 基本语法(简单案例)
!注: go中 对变量申明很是严格,申明了,在没有使用的情况下,也会产生编译错误 1.行分隔符 一行就是代码,无;分割,如果需要在一行展示,需要以;分割,…...
Permute 3 for mac音视频格式转换
Permute是一款Mac平台上的媒体格式转换软件,由Chaotic Software开发。它可以帮助用户快速地将各种音频、视频和图像文件转换成所需格式,并提供了一些常用工具以便于用户进行编辑和处理。 Permute的主要特点包括: - 支持大量格式:支…...

线程概念linux
何为线程: 线程是程序中负责执行的单位,它可以被看作是进程的一部分,是进程的子任务。线程与进程的区别在于,进程是一个资源单位,而线程是进程的一部分,它只有栈这个独立的资源,其他资源如代码…...
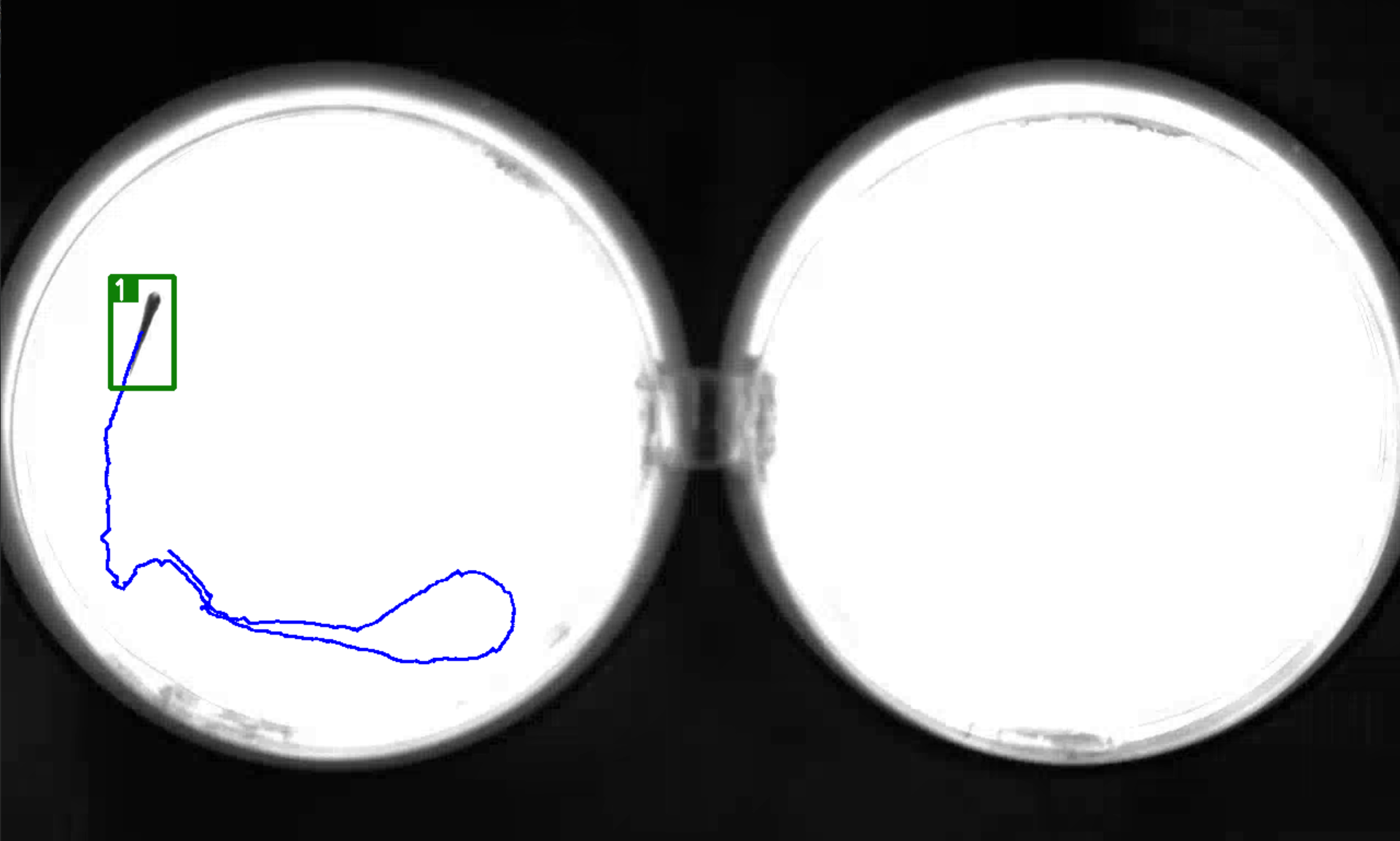
【Yolov5+Deepsort】训练自己的数据集(1)| 目标检测追踪 | 轨迹绘制
📢前言:本篇是关于如何使用YoloV5Deepsort训练自己的数据集,从而实现目标检测与目标追踪,并绘制出物体的运动轨迹。本章讲解的为第一个内容:简单介绍YoloV5Deepsort中所用到的目标检测,追踪及sort&Depp…...
express学习笔记4 - 热更新以及express-boom
我们每次改动代码的时候都要重启项目,现在我们给项目添加一个热更新 npm install --save-dev nodemon # or using yarn: yarn add nodemon -D 在package.json添加一行代码 "dev": "nodemon ./bin/www" 重启项目 然后随便做改动ÿ…...
)
Ajax_02学习笔记(源码 + 图书管理业务 + 以及 个人信息修改功能)
Ajax_02 01_Bootstrap框架-控制弹框的使用 代码 <!-- 引入bootstrap.css --> <link href"https://cdn.jsdelivr.net/npm/bootstrap5.2.2/dist/css/bootstrap.min.css" rel"stylesheet"><button type"button" class"btn btn…...

Python-数据类型转换
当涉及数据类型转换时,Python提供了多种内置函数来执行不同类型之间的转换 以下是每个方法的详细说明和示例案例 整数和浮点数转换: int(x, base10): 将给定的参数x转换为整数。x可以是一个整数、浮点数或字符串。如果x是字符串,则可以提供…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
