刷题记录:牛客NC51101Lost Cows
传送门:牛客
题目描述:
(2≤N≤8,000) cows have unique brands in the range 1..N. In a spectacular display of poor judgment,
they visited the neighborhood 'watering hole' and drank a few too many beers before dinner. When it
was time to line up for their evening meal, they did not line up in the required ascending numerical
order of their brands.
Regrettably, FJ does not have a way to sort them. Furthermore, he's not very good at observing
problems. Instead of writing down each cow's brand, he determined a rather silly statistic: For each
cow in line, he knows the number of cows that precede that cow in line that do, in fact, have smaller
brands than that cow.
Given this data, tell FJ the exact ordering of the cows.
输入
5
1
2
1
0
输出:
2
4
5
3
1
方法一
首先本题有一个比较显然的解决方法,我们可以从最后一个人开始为他定编号,因为对于最后一个人来说,如果他选了aaa编号,那么对于它的前面的人来说,此时除了aaa,所有剩下的编号肯定都是有的,那么就说明我们现在的aaa编号在我们剩下的所有的编号的位置(从小到大)就是当前这个人前面比他小的个数+1.
那么此时我们的问题就变成了如何找出一段序列中排名为kkk的数字,并且支持单点删除操作.对于这个问题,我在这道题中有详细的解释,所以此处就不在赘述了.具体可参考代码
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3fc
struct Segment_tree{int l,r,sum;
}tree[maxn];
int n;
void pushup(int rt) {tree[rt].sum=tree[ls].sum+tree[rs].sum;
}
void build(int l,int r,int rt) {tree[rt].l=l;tree[rt].r=r;if(l==r) {tree[rt].sum=1;return ;}int mid=(tree[rt].l+tree[rt].r)>>1;build(lson);build(rson);pushup(rt);
}
void update(int pos,int rt) {if(tree[rt].l==pos&&tree[rt].r==pos) {tree[rt].sum=0;return ;}int mid=(tree[rt].l+tree[rt].r)>>1;if(pos<=mid) update(pos,ls);else update(pos,rs);pushup(rt);
}
int query(int l,int r,int rt,int k) {if(tree[rt].l==tree[rt].r) return tree[rt].l;int mid=(tree[rt].l+tree[rt].r)>>1;if(tree[ls].sum>=k) return query(l,mid,ls,k);else return query(mid+1,r,rs,k-tree[ls].sum);
}
int ans[maxn];int a[maxn];
int main() {n=read();build(root);for(int i=2;i<=n;i++) a[i]=read();for(int i=n;i>=2;i--) {ans[i]=query(1,n,1,a[i]+1);update(ans[i],1);}ans[1]=query(1,n,1,1);for(int i=1;i<=n;i++) {printf("%d\n",ans[i]);}return 0;
}
方法二
我们可以反向的去思考这道题.我们此时考虑对排在前iii位的人分配我们的相对编号大小.那么对于第iii个人来说,我们之前的所有i−1i-1i−1位人显然都是排在这个人前面的,所以我们要将第iii个人插在i−1i-1i−1排好的编号之中,并且满足当前的需求即可.因为对于插入操作来说,我们并不影响之前的i−1i-1i−1的相对编号大小.
以样例为例(下标为编号):
对于第一只奶牛,在它之前没有奶牛,所以编号为1:1
对于第二只奶牛,在它之前有1只奶牛编号比它小,所以编号为2:1 2
对于第三只奶牛,在它之前有2只奶牛编号比它小,在它之前实际也只有两只奶牛,所以编号为3:1 2 3
对于第四只奶牛,由样例,在它之前有1只奶牛编号比它小,而在他前面有三个奶牛,所以此时它的编号应该大于三个奶牛中的两个,所以此时将他的编号赋为4,其他奶牛编号顺延:1 4 2 3
对于第五只奶牛,解决方法同第四只,编号赋值为1:5 1 4 2 3
对于插入操作,最优的写法显然是链表,但是由于此题的数据不多,才800080008000,所以此时我们直接使用vectorvectorvector来进行维护依旧是可以接受的,复杂度为n∗(n+1)/2n*(n+1)/2n∗(n+1)/2,差不多为3e73e73e7左右
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
vector<int>v;
int a;int ans[maxn];
int main() {int n=read();v.insert(v.begin(),1);for(int i=2;i<=n;i++) {a=read();v.insert(v.begin()+a,i);}for(int i=0;i<v.size();i++) {ans[v[i]]=i+1;}for(int i=1;i<=n;i++) {cout<<ans[i]<<endl;}return 0;
}
相关文章:

刷题记录:牛客NC51101Lost Cows
传送门:牛客 题目描述: (2≤N≤8,000) cows have unique brands in the range 1..N. In a spectacular display of poor judgment, they visited the neighborhood watering hole and drank a few too many beers before dinner. When it was time to line up for their ev…...

华为OD机试 - 不等式 | 备考思路,刷题要点,答疑 【新解法】
最近更新的博客 华为OD机试 - 寻找路径 | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 最小叶子节点 | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 对称美学 | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 最近的点 | 备考思路,刷题要点,答疑 【新解法】华…...

GuLi商城-SpringCloud-OpenFeign测试远程调用
1. Feign 简介 Feign 是一个声明式的 HTTP 客户端,它的目的就是让远程调用更加简单。Feign 提供了HTTP请 求的模板,通过编写简单的接口和插入注解,就可以定义好 HTTP 请求的参数、格式、地址等信 息。Feign 整合了 Ribbon(负载…...
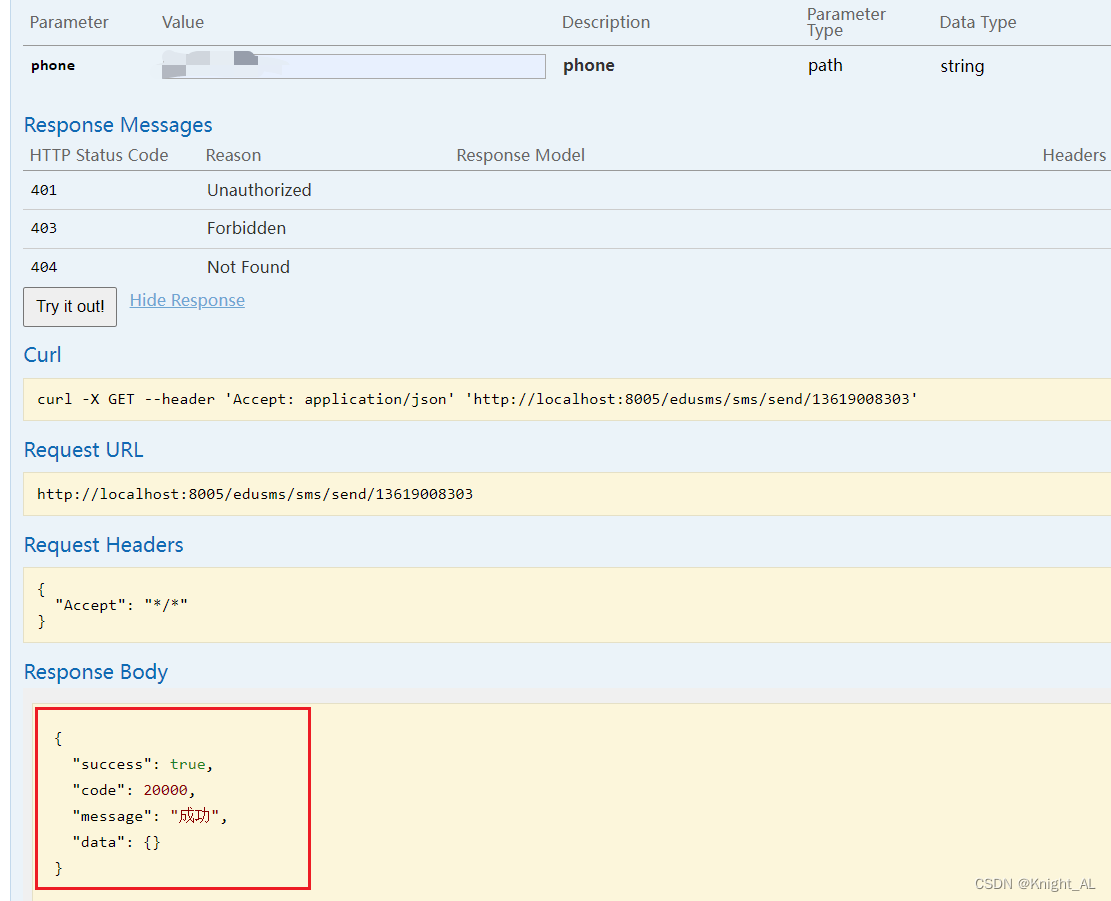
阿里云_山东鼎信短信的使用(云市场)
目录山东鼎信API工具类随机验证码工具类进行测试Pom依赖(可以先导入依赖)创建controllerSmsServiceSmsServiceImplswagger测试(也可以使用postman)山东鼎信API工具类 山东鼎信短信官网 找到java的Api,复制下来 适当改了一下,为了调用(类名SmsUtils) p…...

基于虚拟机机的代码保护技术
虚拟机保护技术是基于x86汇编系统的可执行代码转换为字节码指令系统的代码,以达到保护原有指令不被轻易逆向和篡改的目的。 字节码(Byte-code)是一种包含执行程序,由一序列 op 代码/数据对组成的 ,是一种中间码。字节是…...
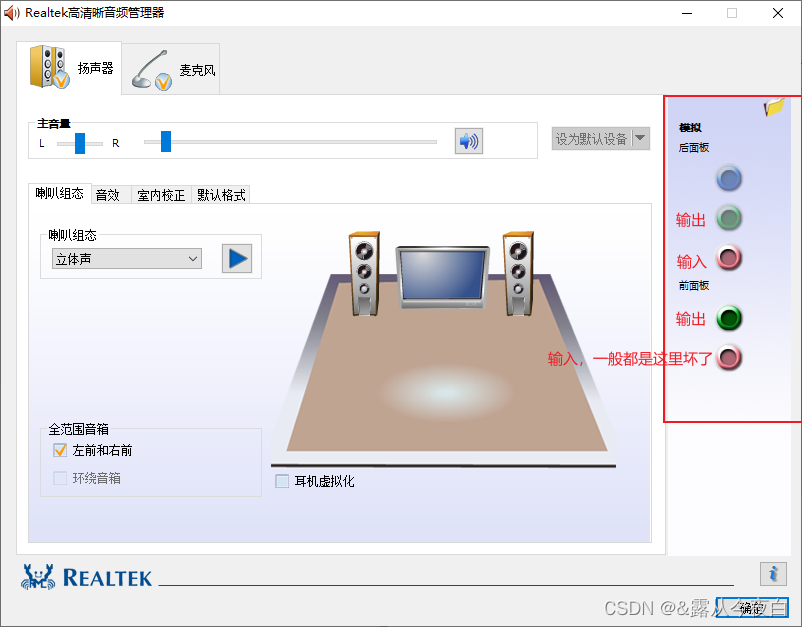
Win10耳机有声音麦不能说话怎么办?麦克风说话别人听不到解决方法
网上找了一些解决办法,一般都是重复的,几个设置调来调去也就那样,没什么用 这种问题一般是“老式”一点的台式机会出现,提供的解决办法如下: 首先下载带面板的音频管理器,如realtek高清晰音频管理器&…...
 Final Round 题解)
The 22nd Japanese Olympiad in Informatics (JOI 2022/2023) Final Round 题解
交题:https://cms.ioi-jp.org/documentation A 给一个序列 a1,⋯,ana_1,\cdots,a_na1,⋯,an。 执行nnn个操作,第iii个操作为找出第iii个数前离其最近且与它相同的数的位置,把这两个数之间的数全部赋值aia_iai。求最后的序列。 考虑第…...

openEuler RISC-V 成功适配 VisionFive 2 单板计算机
近日,RISC-V SIG 成功在 VisionFive 2 开发板上适配欧拉操作系统,目前最新版本的 openEuler RISC-V 22.03 V2 镜像已在 VisionFive 2 开发板上可用,这是 openEuler 推动 RISC-V 生态演进的又一新进展。下载链接https://mirror.iscas.ac.c…...
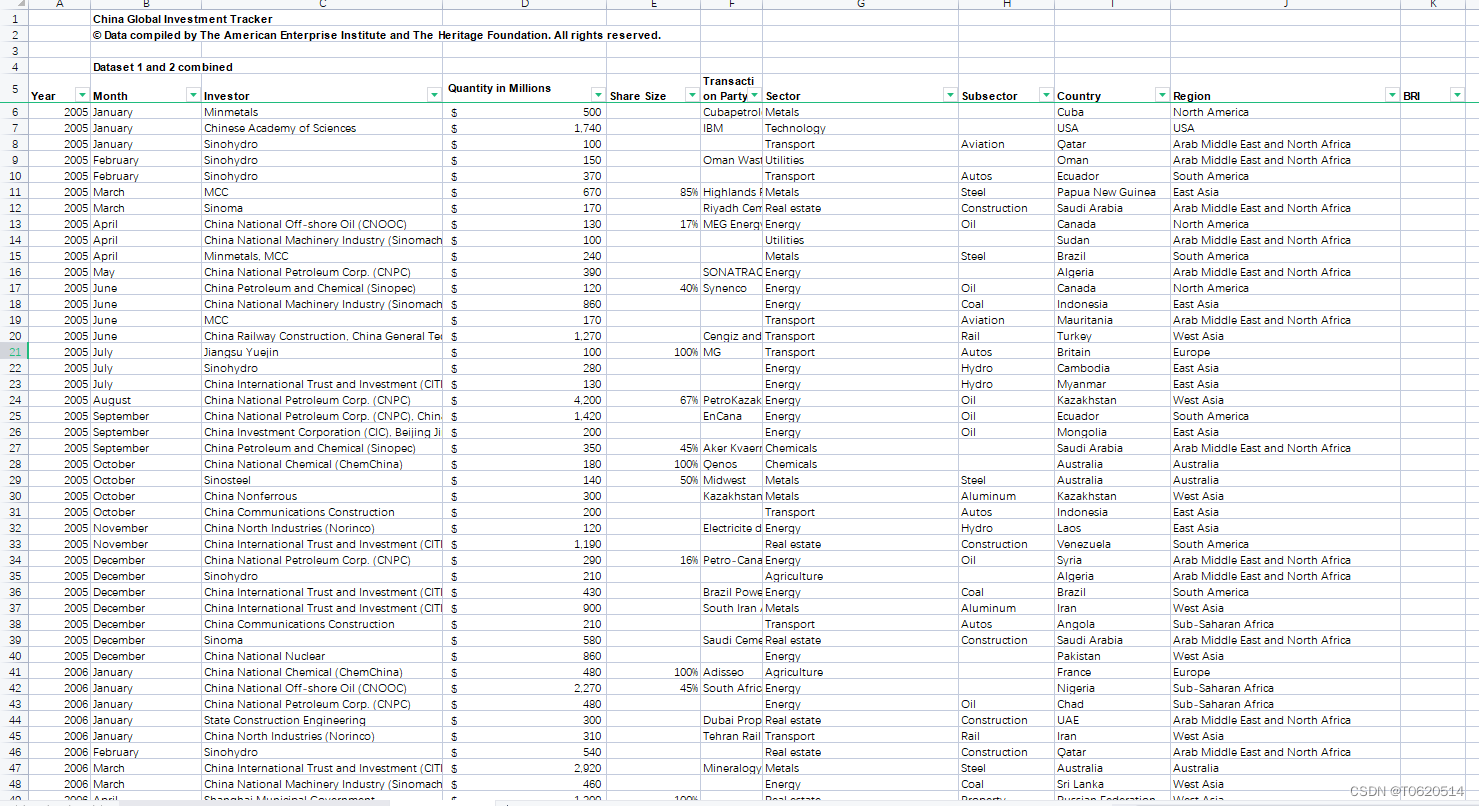
2005-2022中国企业对外直接投资、OFDI海外投资明细、中国全球投资追踪数据CGIT(含非建筑施工类问题投资)
中国全球投资跟踪”(China Global Investment Tracker),数据库,美国企业研究所于1月28日发布。数据库显示,2005年以来,中国对外投资和建设总额已接近2万亿美元。该数据库是唯一一套涵盖中国全球投资和建设的…...
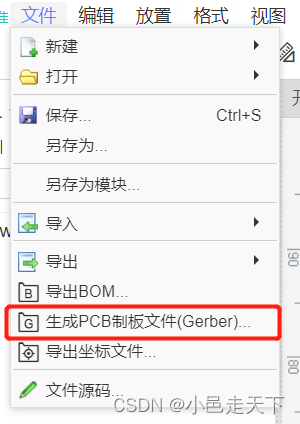
PCB学习笔记——使用嘉立创在线绘制原理图与PCB
嘉立创软件地址:https://lceda.cn/ 新建工程-新建原理图,在元件库中可以搜索元器件,可以直接放置在原理图上。 原理图绘制完成后,保存文件,设计-原理图转PCB,可以直接生成对应的PCB,设置边框&…...

【C++】类型转化
🌈欢迎来到C专栏~~类型转化 (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort目前状态:大三非科班啃C中🌍博客主页:张小姐的猫~江湖背景快上车🚘,握好方向盘跟我有一起打天下嘞!送给自己的一句鸡汤&…...

Mybatis -- resultMap以及分页
查询为null问题 要解决的问题:属性名和字段名不一致 环境:新建一个项目,将之前的项目拷贝过来 1、查看数据库的字段名 2、Java中的实体类设计 public class User { private int id; //id private String name; //姓名 private String passwo…...
Linux之进程
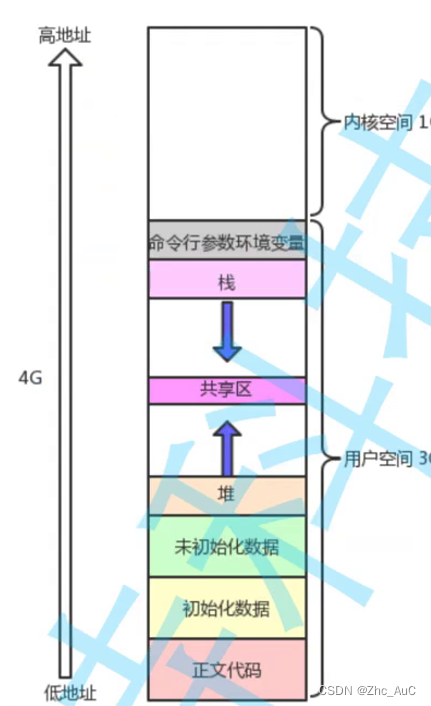
一.冯诺依曼体系 在计算机中,CPU(中央处理器)是不直接跟外部设备直接进行通信的,因为CPU处理速度太快了,而设备的数据读取和输入有太慢,而是CPU以及外设直接跟存储器(内存)打交道&am…...

结构体——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容是结构体噢,之前我们在初始C语言中其实就已经学习过了结构体的知识,但是不是很全面,这次,我们也只是稍微详细一点,敬请期待小雅兰之后的博客ÿ…...

CCNP350-401学习笔记(51-100题)
51、Which statement about a fabric access point is true?A. It is in local mode and must be connected directly to the fabric edge switch. B. It is in local mode and must be connected directly to the fabric border node C. It is in FlexConnect mode and must …...
C语言学习_DAY_4_判断语句if_else和分支语句switch_case【C语言学习笔记】
高质量博主,点个关注不迷路🌸🌸🌸! 目录 1.案例引入 2.if判断语句的语法与注意事项 3.switch多分支语句的语法与注意事项 前言: 书接上回,我们已经学习了所有的数据类型、运算符,并且可以书写…...
)
实验07 赫夫曼编码及综合2022(带程序填空)
A. 【程序填空】赫夫曼编码题目描述给定n个叶子的权值,根据这些权值构造huffman树,并输出huffman编码参考课本第6.6节的算法6.12,注意算法中数组访问是从位置1开始赫夫曼构建中,默认左孩子权值不大于右孩子权值如果遇到两个孩子权…...
分布式 CAP BASE理论
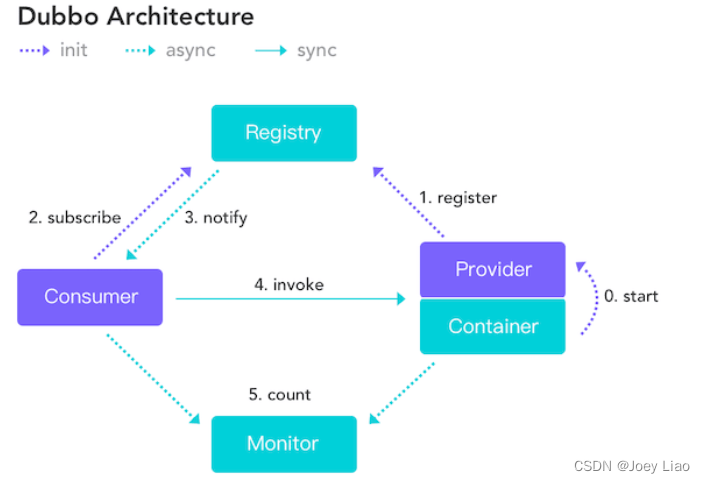
文章目录CAP简介不是所谓的“3 选 2”CAP 实际应用案例BASE简介BASE 理论的核心思想总结CAP 简介 在理论计算机科学中,CAP 定理(CAP theorem)指出对于一个分布式系统来说,当设计读写操作时,只能同时满足以下三点中的…...

三调地类筛选器,Arcgis地类筛选
三调地类在使用是,需要分类统计,这个可以用于筛选; 标准地类筛选 农用地: DLBM IN(0303,0304,0306,0402,0101,0102,0103,0201,0201K,0202,0202K,0203,0203K,0204,0204K,0301,0301K,0302,0302K,0305,0307,0307K,0401,0403,0403K…...
)
华为OD机试 - 密室逃生游戏(Python)
密室逃生游戏 题目 小强增在参加《密室逃生》游戏,当前关卡要求找到符合给定 密码 K(升序的不重复小写字母组成) 的箱子, 并给出箱子编号,箱子编号为 1~N 。 每个箱子中都有一个 字符串 s ,字符串由大写字母、小写字母、数字、标点符号、空格组成, 需要在这些字符串中…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
