【RL】Wasserstein距离-GAN背后的直觉
一、说明
在本文中,我们将阅读有关Wasserstein GANs的信息。具体来说,我们将关注以下内容:i)什么是瓦瑟斯坦距离?,ii)为什么要使用它?iii) 我们如何使用它来训练 GAN?
二、Wasserstein距离概念
Wasserstein距离,又称为Earth Mover's Distance (EMD),是衡量两个概率分布之间的差异程度的一种数学方式。它考虑了分布之间的距离和它们之间的“传输成本”。
简单来说,Wasserstein距离将两个分布看作“堆积在地图上的土堆”,并计算将一个堆移到另一个的最小成本。这个距离度量的优点是它能够处理非均匀分布,并且能够考虑分布的形状和结构。
Wasserstein距离在机器学习领域中应用非常广泛,特别是在生成模型中用来评估生成器生成的图像与真实图像之间的差异。
2.1 瓦瑟施泰因距离
Wasserstein 距离(地球移动器的距离)是给定度量空间上两个概率分布之间的距离度量。直观地说,它可以被视为将一个分布转换为另一个分布所需的最小功,其中功被定义为必须移动的分布的质量和要移动的距离的乘积。在数学上,它被定义为:

在方程1中,Π(P_r,P_g)是x和y上所有联合分布的集合,使得边际分布等于P_r和P_g。 γ(x, y)可以看作是必须从x移动到y才能将P_r转换为P_g的质量量[1]。因此,瓦瑟斯坦距离是最佳运输计划的成本。
2.2 瓦瑟斯坦距离 vs. 詹森-香农分歧
最初的GAN目标被证明是Jensen-Shannon分歧的最小化[2]。JS背离定义为:

与JS相比,Wasserstein距离具有以下优点:
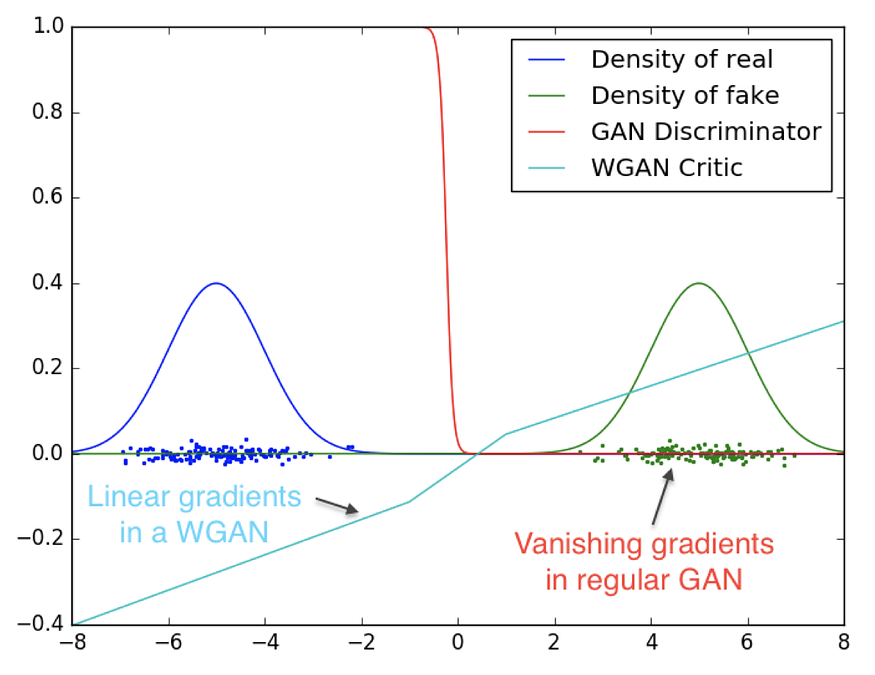
- Wasserstein 距离是连续的,几乎可以在任何地方微分,这使我们能够训练模型达到最佳状态。
- 随着鉴别器的变好,JS散度局部饱和,因此梯度变为零并消失。
- Wasserstein 距离是一个有意义的度量,即当分布彼此靠近时,它收敛到 0,当它们越来越远时发散。
- 作为目标函数的 Wasserstein 距离比使用 JS 散度更稳定。当使用Wasserstein距离作为目标函数时,模式崩溃问题也得到了缓解。
从图 1 我们清楚地看到,最佳GAN鉴别器饱和并导致梯度消失,而优化Wasserstein距离的WGAN评论家在整个过程中具有稳定的梯度。
有关数学证明和更详细的研究,请查看此处的论文!
三、瓦瑟斯坦·GAN
现在可以清楚地看到,优化 Wasserstein 距离比优化 JS 散度更有意义,还需要注意的是,方程 1 中定义的 Wasserstein 距离非常棘手[3],因为我们不可能计算所有 γ ∈Π(Pr ,Pg) 的下界(最大下界)。然而,从坎托罗维奇-鲁宾斯坦二元性中,我们有,
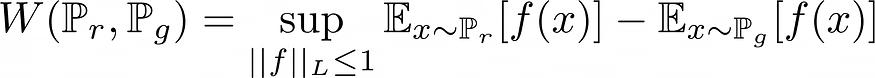
这里我们有 W(P_r, P_g) 作为所有 1-Lipschitz 函数 f: X → R 的上确界(最低上限)。
K-利普希茨连续性:给定 2 个度量空间 (X, d_X) 和 (Y, d_Y),变换函数 f: X → Y 是 K-利普希茨连续的,如果
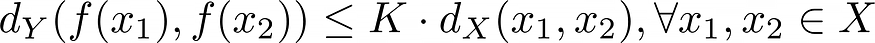
其中d_X和d_Y是各自度量空间中的距离函数。当一个函数是 K-Lipschitz 时,从方程 2 开始,我们最终得到 K ∙ W(P_r, P_g)。
现在,如果我们有一系列参数化函数 {f_w},其中 w∈W 是 K-Lipschitz 连续的,我们可以有

即,w∈W 最大化方程 4 给出瓦瑟斯坦距离乘以一个常数。
四、WGAN评论家
为此,WGAN引入了一个批评者,而不是我们在GAN中了解到的鉴别器。批评者网络在设计上类似于判别器网络,但通过优化找到将最大化方程 4 的 w* 来预测 Wasserstein 距离。为此,批评家的客观功能如下:

在这里,为了在函数f上强制执行Lipschitz连续性,作者诉诸于将权重w限制在一个紧凑的空间内。这是通过将砝码夹紧到一个小范围(论文中的[-1e-2,1e-2][1])来完成的。
鉴别器和批评者之间的区别在于,鉴别器经过训练以正确识别P_r样本和P_g样本,批评家估计P_r和P_g之间的Wasserstein距离。
这是训练批评家的python代码。
for ix in n_critic_steps:opt_critic.zero_grad()real_images = data[0].float().to(device)# * Generate imagesnoise = sample_noise()fake_images = netG(noise)# * though they are name so, they are not logits!real_logits = netCritic(real_images)fake_logits = netCritic(fake_images)# * max E_{x~P_X}[C(x)] - E_{Z~P_Z}[C(g(z))]loss = -(real_logits.mean() - fake_logits.mean())loss.backward(retain_graph=True)opt_critic.step()# * Gradient clipplingfor p in netCritic.parameters():p.data.clamp_(-self.c, self.c)五、WGAN生成器目标
当然,发电机的目标是最小化P_r和P_g之间的瓦瑟斯坦距离。生成器试图找到最小化P_g和P_r之间的 Wasserstein 距离的 θ*。为此,生成器的目标函数如下:
![]()
公式 6:生成器目标函数。
在这里,WGAN生成器和标准生成器之间的主要区别再次在于,WGAN生成器试图最小化P_r和P_g之间的Wasserstein距离,而标准生成器试图用生成的图像欺骗鉴别器。
以下是训练生成器的 python 代码:
opt_gen.zero_grad()noise = sample_noise()fake_images = netG(noise)# again, these are not logits.
fake_logits = netCritic(fake_images)# * - E_{Z~P_Z}[C(g(z))]
loss = -fake_logits.mean().view(-1)loss.backward()
opt_gen.step()六、培训结果

图例.2显示了训练WGAN的一些早期结果。请注意,图 2 中的图像是早期结果,一旦确认模型按预期训练,训练就会停止。
七、代码
Wasserstein GAN的完整实现可以在这里找到[3]。
八、结论
WGAN提供非常稳定的培训和有意义的培训目标。本文介绍并直观地解释了什么是 Wasserstein 距离,Wasserstein 距离相对于标准 GAN 使用的 Jensen-Shannon 散度的优势,以及如何使用 Wasserstein 距离来训练 WGAN。我们还看到了用于训练 Critic 和生成器的代码片段,以及早期训练模型的大量输出。尽管WGAN比标准GAN具有许多优势,但WGAN论文的作者明确承认,权重裁剪不是执行Lipschitz连续性的最佳方法[1]。为了解决这个问题,他们提出了带有梯度惩罚的Wasserstein GAN[4],我们将在后面的文章中讨论。
如果您喜欢这个,请查看本系列的下一篇文章,其中讨论了 WGAN-GP!
相关文章:

【RL】Wasserstein距离-GAN背后的直觉
一、说明 在本文中,我们将阅读有关Wasserstein GANs的信息。具体来说,我们将关注以下内容:i)什么是瓦瑟斯坦距离?,ii)为什么要使用它?iii) 我们如何使用它来训练 GAN&…...

sentinel引入CommonFilter类
最近在做一个springcloudAlibaba项目,做链路流控模式时需要将入口资源关闭聚合,做法如下: spring-cloud-alibaba v2.1.1.RELEASE及前,sentinel1.7.0及后: 1.pom 中引入: <dependency><groupId>…...

Phoenix创建local index失败
执行创建local index出现如下错误 0: jdbc:phoenix:hbase01:2181> create local index local_index_name on "test" ("user"."name","user"."address"); 23/07/28 17:28:56 WARN client.SyncCoprocessorRpcChannel: Cal…...

css3 hover border 流动效果
/* Hover 边线流动 */.hoverDrawLine {border: 0 !important;position: relative;border-radius: 5px;--border-color: #60daaa; } .hoverDrawLine::before, .hoverDrawLine::after {box-sizing: border-box;content: ;position: absolute;border: 2px solid transparent;borde…...

jdk安装
JDK的下载、安装和环境配置教程(2021年,win10)_「已注销」的博客-CSDN博客_jdk 以上文章如果没有成功在环境变量中part再添加一句 C:\Program Files (x86)\Java\jdk1.7.0_80\bin 安装目录下的bin目录 写完环境后重启 📎jdk-20_w…...

utf8mb4_general_ci 和utf8mb4_unicode_ci有什么异同,有什么优劣
utf8mb4_general_ci 和 utf8mb4_unicode_ci 都是 MySQL 数据库中的字符集和排序规则(collation)。它们主要用于指定字符数据的排序和比较规则,以确保在数据库中对字符串进行查询和比较时得到正确的结果。 异同点: 1. utf8mb4_gen…...
java实现钉钉群机器人@机器人获取信息后,机器人回复(机器人接收消息)
1.需求 鉴于需要使用钉钉群机器人回复,人们提出的问题,需要识别提出的问题中的关键词,后端进行处理实现对应的业务逻辑 2.实现方式 用户群机器人,附带提出的问题,后端接收消息后识别消息内容,读取到关键…...

ffmpeg转码时出现missing picture in access unit with size 14019
使用ffmpeg录制网络流视频,因为网卡的缘故导致录制中断,视频在转换的时候就出现这个问题。 missing picture in access unit with size 14019怀疑是在最后的地方视频是损坏的,索性截取掉最后的2秒时间,原本视频时长是02:06:28&am…...

以Llama-2为例,在生成模型中使用自定义StoppingCriteria
以Llama-2为例,在生成模型中使用自定义StoppingCriteria 1. 前言2. 场景介绍3. 解决方法4. 结语 1. 前言 在之前的文章中,介绍了使用transformers模块创建的模型,其generate方法的详细原理和使用方法,文章链接: 以be…...

servlet接受参数和乱码问题
servlet接受参数和乱码问题 1、乱码问题 1)get请求 传输参数出现中文乱码问题: 如果还存在问题: 2)post请求 传输参数出现中文乱码问题: 2、接受参数: 3、登录注册案例...

2023-08-05力扣今日三题
链接: 剑指 Offer 22. 链表中倒数第k个节点 题意: 如题 解: 快慢指针 实际代码: #include<iostream> using namespace std; struct ListNode {int val;ListNode *next;ListNode(int x) : val(x), next(NULL) {} }; L…...

webpack图片压缩
减少代码体积 | 尚硅谷 Web 前端之 Webpack5 教程 (yk2012.github.io) npm install image-mininizer webpack plugin imagemin -D 无损压缩 npm install imagemin-gifsicle imagemin-jpegtran imagemin-optipng imagemin-svgo -D 有损压缩 npm install imagemin-gifsicle image…...

JPA使用nativeQuery自定义SQL怎么插入一个对象参数呢?
0、我们在前后端传递数据时候,参数多的情况下,常常将这些参数封装成对象;当有些场景你需要使用JPA nativeQuery自定义SQL,要将这个对象insert时候,初学者似乎有点犯难,jpa不是spring-data项目的内容吗&…...

用C语言构建一个数字识别卷积神经网络
卷积神经网络的具体原理和对应的python例子参见末尾的参考资料2.3. 这里仅叙述卷积神经网络的配置, 其余部分不做赘述,构建和训练神经网络的具体步骤请参见上一篇: 用C语言构建一个手写数字识别神经网路 卷积网络同样采用简单的三层结构,包括输入层con…...
【CSS】圆形放大的hover效果
效果 index.html <!DOCTYPE html> <html><head><title> Document </title><link type"text/css" rel"styleSheet" href"index.css" /></head><body><div class"avatar"></…...

work weekly
每周汇报:围绕着项目范围及需求内容完成情况多少、人力资源情况、整体进度情况、成本情况、【范围】多少工作、【资源】投入多少人、【时间】花费多少时间、【成本】花了多少钱 【质量】一般没有特别要求的默认软件开发过程规范要求响应时间 【沟通】这里不说了 …...
Mac端口扫描工具
端口扫描工具 Mac内置了一个网络工具 网络使用工具 按住 Command 空格 然后搜索 “网络实用工具” 或 “Network Utility” 即可 域名/ip转换Lookup ping功能 端口扫描 https://zhhll.icu/2022/Mac/端口扫描工具/ 本文由 mdnice 多平台发布...
如何隐藏开源流媒体EasyPlayer.js视频H.265播放器的实时录像按钮?
目前我们TSINGSEE青犀视频所有的视频监控平台,集成的都是EasyPlayer.js版播放器,它属于一款高效、精炼、稳定且免费的流媒体播放器,可支持多种流媒体协议播放,包括WebSocket-FLV、HTTP-FLV,HLS(m3u8&#x…...
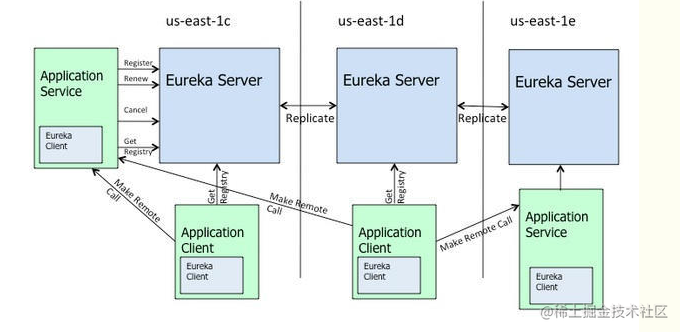
Spring Cloud Eureka 和 zookeeper 的区别
CAP理论 在了解eureka和zookeeper区别之前,我们先来了解一下这个知识,cap理论。 1998年的加州大学的计算机科学家 Eric Brewer 提出,分布式有三个指标。Consistency,Availability,Partition tolerance。简称即为CAP。…...

Golang之路---04 并发编程——信道/通道
信道/通道 如果说 goroutine 是 Go语言程序的并发体的话,那么 channel(信道) 就是 它们之间的通信机制。channel,是一个可以让一个 goroutine 与另一个 goroutine 传输信息的通道,我把他叫做信道,也有人将…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
