【LeetCode】647. 回文子串
题目链接
文章目录
- 1. 思路讲解
- 1.1 方法选择
- 1.2 dp表的创建
- 1.3 状态转移方程
- 1.4 填表顺序
- 2. 代码实现
1. 思路讲解
1.1 方法选择
这道题我们采用动态规划的解法,倒不是动态规划的解法对于这道题有多好,它并不是最优解。但是,这道题的动态规划思想是非常有用的,我们使用这道题的动态规划思想,可以让一些hard题变为easy题。
也就是说,这道题的动态规划思想其实就是起到了一个抛砖引玉的作用。
1.2 dp表的创建
如何表示出所有的子串的情况?可以用 i 表示某个子串的起始位置,用 j 来表示某个子串的末尾位置,暴力枚举,可以在N^2的时间复杂度内求出所有子串是否为回文子串。
所以,我们用二维dp[i][j]表来表示,以 i 位置为起始位置且以 j 位置为结尾的子串是否为回文子串。如果为回文子串那么dp[i][j]为true,否则为false。(我们人为规定 i <= j)
1.3 状态转移方程
我们要知道dp[i][j]为是否为回文子串,首先要判断 s[i] 是否等于 s[j]。
如果 s[i] != s[j],那么不管 i 和 j 中间的元素序列是怎样的,以 i 位置为起始位置,以 j 位置为终止位置的子串一定不为回文子串。
如果 s[i] == s[j],那么需要对 i 和 j 的位置进行判断。
- 如果 i == j,那么说明当前初识位置和末尾位置在同一个位置,也就是说,子串只有一个元素,此时根据题意它为回文子串;
- 如果 i + 1 == j,那么 i 和 j 的位置是相邻的,此时它们中间没有元素,它们位置上的元素又相同,那么一定是回文子串;
- 如果 i + 1 < j,说明 i 位置 和 j 位置中间还有其他元素,此时只需判断dp[i+1][j-1]为true还是false即可。
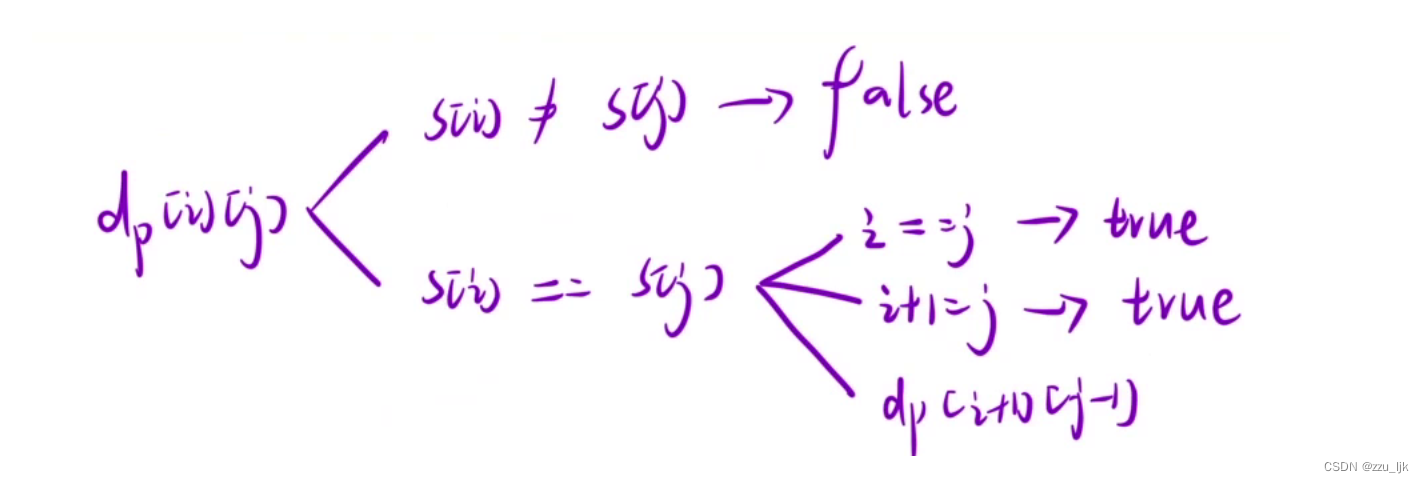
1.4 填表顺序
由于我们求dp[i][j]的时候,需要用到 dp[i+1][j-1],且 i 的循环为外层的循环,所以让 i 从大到小循环即可。
2. 代码实现
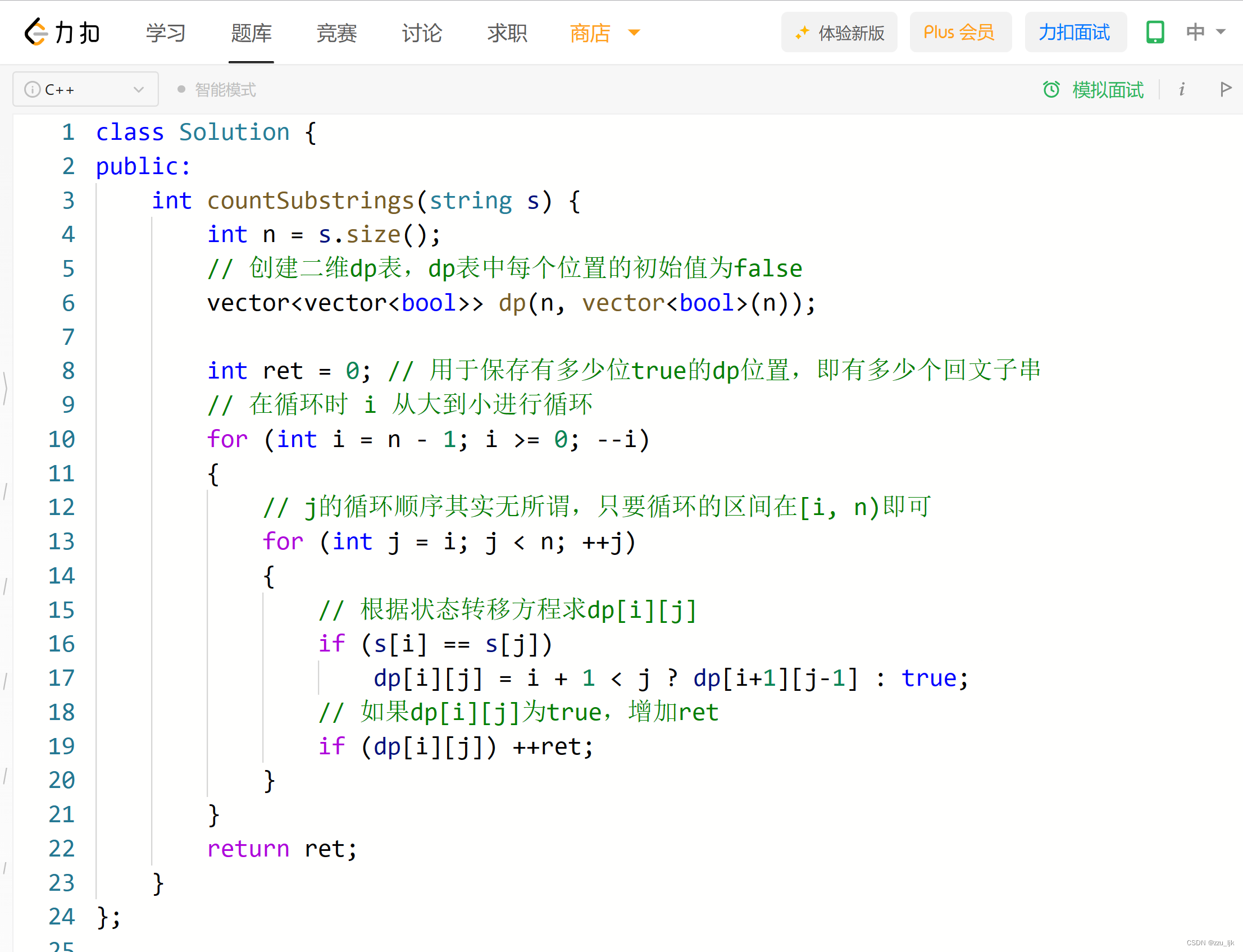
class Solution {
public:int countSubstrings(string s) {int n = s.size();// 创建二维dp表,dp表中每个位置的初始值为falsevector<vector<bool>> dp(n, vector<bool>(n));int ret = 0; // 用于保存有多少位true的dp位置,即有多少个回文子串// 在循环时 i 从大到小进行循环for (int i = n - 1; i >= 0; --i){// j的循环顺序其实无所谓,只要循环的区间在[i, n)即可for (int j = i; j < n; ++j){// 根据状态转移方程求dp[i][j]if (s[i] == s[j])dp[i][j] = i + 1 < j ? dp[i+1][j-1] : true;// 如果dp[i][j]为true,增加retif (dp[i][j]) ++ret;}}return ret;}
};
相关文章:

【LeetCode】647. 回文子串
题目链接 文章目录 1. 思路讲解1.1 方法选择1.2 dp表的创建1.3 状态转移方程1.4 填表顺序 2. 代码实现 1. 思路讲解 1.1 方法选择 这道题我们采用动态规划的解法,倒不是动态规划的解法对于这道题有多好,它并不是最优解。但是,这道题的动态…...
 角度制与弧度制的相互转换)
Open3D(C++) 角度制与弧度制的相互转换
目录 一、弧度转角度1、计算公式2、主要函数3、示例代码4、结果展示二、角度转弧度1、计算公式2、主要函数3、示例代码4、结果展示三、归一化到(-PI,PI)1、主要函数<...

【小沐学NLP】在线AI绘画网站(网易云课堂:AI绘画工坊)
文章目录 1、简介1.1 参与方式1.2 模型简介 2、使用费用3、操作步骤3.1 选择模型3.2 输入提示词3.3 调整参数3.4 图片生成 4、测试例子4.1 小狗4.2 蜘蛛侠4.3 人物4.4 龙猫 结语 1、简介 Stable Diffusion是一种强大的图像生成AI,它可以根据输入的文字描述词&#…...

GNN code Tips
1. 重置label取值范围 problem: otherwise occurs IndexError: target out of bounds # reset labels value range, otherwise occurs IndexError: target out of bounds uni_set torch.unique(labels) to_set torch.tensor(list(range(len(uni_set)))) labels_reset label…...
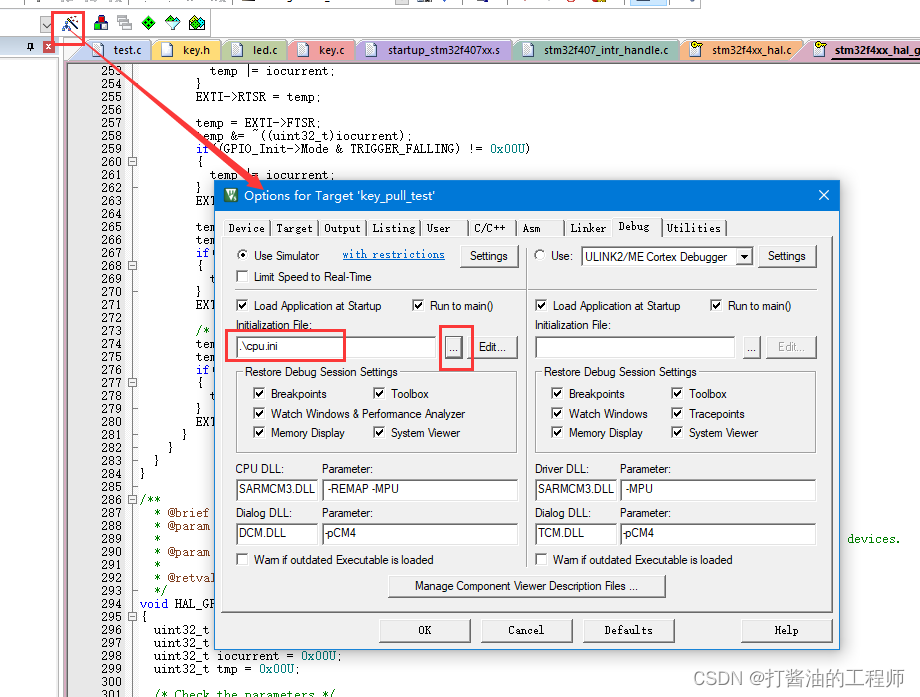
物联网|按键实验---学习I/O的输入及中断的编程|函数说明的格式|如何使用CMSIS的延时|读取通过外部中断实现按键捕获代码的实现及分析-学习笔记(14)
文章目录 通过外部中断实现按键捕获代码的实现及分析Tip1:函数说明的格式Tip2:如何使用CMSIS的延时GetTick函数原型stm32f407_intr_handle.c解析中断处理函数:void EXTI4_IRQHandler 调试流程软件模拟调试 两种代码的比较课后作业: 通过外部中断实现按键捕获代码的实…...

Java对象的前世今生
文章目录 一、创建对象的步骤二、类加载机制三、内存分配指针碰撞 (内存连续)空闲列表 (内存不连续) 四、创建对象的5种方法五、浅拷贝与深拷贝 以下一行代码内部发生了什么? Person person new Person();一、创建对象的步骤 根据JLS中的规定,Java对象…...

Qt中JSON的使用
一.前言: JSON是一种轻量级数据交换格式,常用于客户端和服务端的数据交互,不依赖于编程语言,在很多编程语言中都可以使用JSON,比如C,C,Java,Android,Qt。除了JSON&#x…...

linux安装Tomcat部署jpress教程
yum在线安装: 查看tomcat相关的安装包: [rootRHCE ~]# yum list | grep -i tomcat tomcat.noarch 7.0.76-16.el7_9 updates tomcat-el-2.2-api.noarch 7.0.76-16.el7_9 updat…...

高并发负载均衡---LVS
目录 前言 一:负载均衡概述 二:为啥负载均衡服务器这么快呢? 编辑 2.1 七层应用程序慢的原因 2.2 四层负载均衡器LVS快的原因 三:LVS负载均衡器的三种模式 3.1 NAT模式 3.1.1 什么是NAT模式 3.1.2 NAT模式实现LVS的缺点…...

微前端中的 CSS
本文为翻译 本文译者为 360 奇舞团前端开发工程师原文标题:CSS in Micro Frontends 原文作者:Florian Rappl 原文地址:https://dev.to/florianrappl/css-in-micro-frontends-4jai 我被问得最多的问题之一是如何在微前端中处理 CSS。毕竟&…...
)
在CSDN学Golang场景化解决方案(分布式日志系统)
一,传统 elk 解决方案及其弊端 传统ELK(Elasticsearch Logstash Kibana)方案是一种流行的分布式日志系统解决方案,但也存在一些弊端: 依赖性:ELK使用Java编写,需要安装JVM,并且还…...

电脑第一次使用屏幕键盘
操作流程 1.在键盘上同时按WinR打开运行; 2.输入control 3.找到设置中心 4.点击屏幕键盘 效果 具体怎么使用 我不咋清除 简单 测试了一下 可以用鼠标点击屏幕键盘的按键 用键盘 按字母键和数字键 是和屏幕键盘不同步的 其他 tab、shift、后退、enter好像同步...

【C#学习笔记】类型转换
文章目录 类型转换字符转数字GetNumericValueConvert.ToInt32隐式转换计算 字符串转数字Parse 或 TryParse 方法 字节数组转整数 as,is强制类型转换isas 用户定义的转换 类型转换 我们简单地将值类型分为5种:整数型,浮点型,布尔型…...

SpringBoot+SSM实战<一>:打造高效便捷的企业级Java外卖订购系统
文章目录 项目简介项目架构功能模块管理端用户端 技术选型用户层网关层应用层数据层工具 项目优缺点结语 黑马程序员最新Java项目实战《苍穹外卖》:让你轻松掌握SpringBootSSM的企业级开发技巧项目简介 《苍穹外卖》是一款为餐饮企业(餐厅、饭店&#x…...

笙默考试管理系统-MyExamTest--calculagraph
笙默考试管理系统-MyExamTest--calculagra(1) 目录 一、 笙默考试管理系统-MyExamTest--calculagra 二、 笙默考试管理系统-MyExamTest--calculagra 三、 笙默考试管理系统-MyExamTest--calculagra 四、 笙默考试管理系统-MyExamTest--calculagra …...

Mysql面试突击班索引,事务与锁
Mysql面试突击班索引,事务与锁 1.为什么Mysql要使用B树做为索引而不用B树 B树能显著减少IO次数,提高效率B树的查询效率更加稳定,因为数据放在叶子节点B树能提高范围查询的效率,因为叶子节点指向下一个叶子节点B树采取顺序读 2.…...
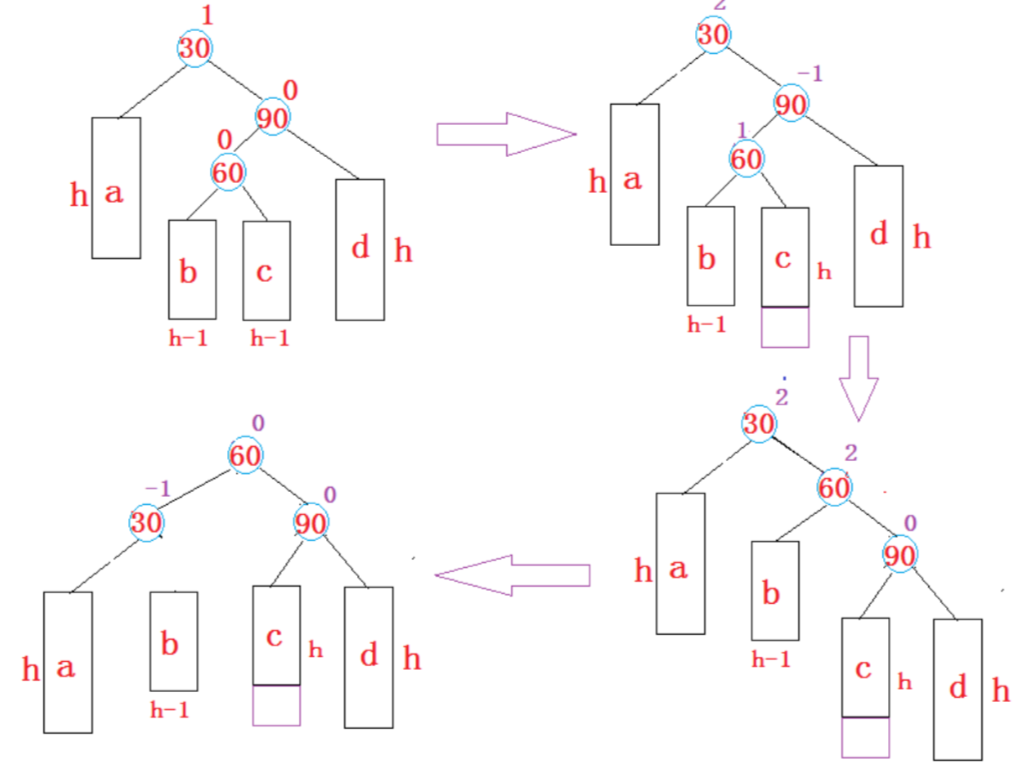
数据结构——AVL树
文章目录 一.AVL树的定义二.AVL树的插入三.插入后更新平衡因子四.AVL树的旋转1.左单旋2.右单旋3.先左单旋再右单旋4.先右单旋再左单旋 五.AVL树的性能分析六.检查是否满足AVL树七.源码 一.AVL树的定义 二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉…...
AI写作宝有哪些,分享两种AI写作工具
AI写作宝是一种基于人工智能技术的写作辅助工具。它可以根据用户输入的关键词和主题快速生成文章。AI写作宝可以为用户节省大量的时间和精力,帮助用户快速生成高质量的文章。今天就为大家推荐两款AI写作宝: 一、AI创作家 AI创作家是一款基于人工智能技…...

【uniapp 控制页面滑动速度】
可以使用 uni-app 提供的 onTouchMove 事件来控制页面滑动速度。 可以在 onTouchMove 事件方法中使用 event.deltaY 计算页面滑动的速度,然后根据需要来调整速度值,最后通过 event.preventDefault() 阻止默认的滑动行为,从而实现控制页面滑动…...
)
7-24 整数的分类处理 (20 分)
7-24 整数的分类处理 (20 分) 给定 N 个正整数,要求你从中得到下列三种计算结果: A1 能被 3 整除的最大整数 A2 存在整数 K 使之可以表示为 3K1 的整数的个数 A3 存在整数 K 使之可以表示为 3K2 的所有整数的平均值(精确到小数…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

使用高斯朴素贝叶斯算法对鸢尾花数据集进行分类
高斯朴素贝叶斯算法通常用于特征变量是连续变量,符合高素分布的情况。 使用高斯朴素贝叶斯算法对鸢尾花数据集进行分类 """ 使用高斯贝叶斯堆鸢尾花进行分类 """ #导入需要的库 from sklearn.datasets import load_iris from skle…...

Redis——主从哨兵配置
目录 基础概念 一、核心原理 二、核心特性 三、技术意义与应用价值 四、典型应用场景 案例部署 一、主从复制配置命令 二、哨兵模式部署命令 关键注意事项 基础概念 一、核心原理 内存存储与高性能 Redis 所有数据存储于内存中&…...
)
Ubuntu挂载本地镜像源(像CentOS 一样挂载本地镜像源)
1.挂载 ISO 镜像 sudo mount -o loop /ubuntu-22.04.5-desktop-amd64.iso /mnt/iso 2.备份现有的软件源配置文件: sudo cp /etc/apt/sources.list /etc/apt/sources.list.bak 3.编辑软件源配置文件 编辑 /etc/apt/sources.list sudo nano /etc/apt/sources.l…...
