线性代数 | 机器学习数学基础
前言
线性代数(linear algebra)是关于向量空间和线性映射的一个数学分支。它包括对线、面和子空间的研究,同时也涉及到所有的向量空间的一般性质。
本文主要介绍机器学习中所用到的线性代数核心基础概念,供读者学习阶段查漏补缺或是快速学习参考。
线性代数
行列式
1.行列式按行(列)展开定理
(1) 设 A = ( a i j ) n × n A = ( a_{{ij}} )_{n \times n} A=(aij)n×n,则: a i 1 A j 1 + a i 2 A j 2 + ⋯ + a i n A j n = { ∣ A ∣ , i = j 0 , i ≠ j a_{i1}A_{j1} +a_{i2}A_{j2} + \cdots + a_{{in}}A_{{jn}} = \begin{cases}|A|,i=j\\ 0,i \neq j\end{cases} ai1Aj1+ai2Aj2+⋯+ainAjn={∣A∣,i=j0,i=j
或 a 1 i A 1 j + a 2 i A 2 j + ⋯ + a n i A n j = { ∣ A ∣ , i = j 0 , i ≠ j a_{1i}A_{1j} + a_{2i}A_{2j} + \cdots + a_{{ni}}A_{{nj}} = \begin{cases}|A|,i=j\\ 0,i \neq j\end{cases} a1iA1j+a2iA2j+⋯+aniAnj={∣A∣,i=j0,i=j即 A A ∗ = A ∗ A = ∣ A ∣ E , AA^{*} = A^{*}A = \left| A \right|E, AA∗=A∗A=∣A∣E,其中: A ∗ = ( A 11 A 12 … A 1 n A 21 A 22 … A 2 n … … … … A n 1 A n 2 … A n n ) = ( A j i ) = ( A i j ) T A^{*} = \begin{pmatrix} A_{11} & A_{12} & \ldots & A_{1n} \\ A_{21} & A_{22} & \ldots & A_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ A_{n1} & A_{n2} & \ldots & A_{{nn}} \\ \end{pmatrix} = (A_{{ji}}) = {(A_{{ij}})}^{T} A∗= A11A21…An1A12A22…An2…………A1nA2n…Ann =(Aji)=(Aij)T
D n = ∣ 1 1 … 1 x 1 x 2 … x n … … … … x 1 n − 1 x 2 n − 1 … x n n − 1 ∣ = ∏ 1 ≤ j < i ≤ n ( x i − x j ) D_{n} = \begin{vmatrix} 1 & 1 & \ldots & 1 \\ x_{1} & x_{2} & \ldots & x_{n} \\ \ldots & \ldots & \ldots & \ldots \\ x_{1}^{n - 1} & x_{2}^{n - 1} & \ldots & x_{n}^{n - 1} \\ \end{vmatrix} = \prod_{1 \leq j < i \leq n}^{}\,(x_{i} - x_{j}) Dn= 1x1…x1n−11x2…x2n−1…………1xn…xnn−1 =∏1≤j<i≤n(xi−xj)
(2) 设 A , B A,B A,B为 n n n阶方阵,则 ∣ A B ∣ = ∣ A ∣ ∣ B ∣ = ∣ B ∣ ∣ A ∣ = ∣ B A ∣ \left| {AB} \right| = \left| A \right|\left| B \right| = \left| B \right|\left| A \right| = \left| {BA} \right| ∣AB∣=∣A∣∣B∣=∣B∣∣A∣=∣BA∣,但 ∣ A ± B ∣ = ∣ A ∣ ± ∣ B ∣ \left| A \pm B \right| = \left| A \right| \pm \left| B \right| ∣A±B∣=∣A∣±∣B∣不一定成立。
(3) ∣ k A ∣ = k n ∣ A ∣ \left| {kA} \right| = k^{n}\left| A \right| ∣kA∣=kn∣A∣, A A A为 n n n阶方阵。
(4) 设 A A A为 n n n阶方阵, ∣ A T ∣ = ∣ A ∣ ; ∣ A − 1 ∣ = ∣ A ∣ − 1 |A^{T}| = |A|;|A^{- 1}| = |A|^{- 1} ∣AT∣=∣A∣;∣A−1∣=∣A∣−1(若 A A A可逆), ∣ A ∗ ∣ = ∣ A ∣ n − 1 |A^{*}| = |A|^{n - 1} ∣A∗∣=∣A∣n−1
n ≥ 2 n \geq 2 n≥2
(5) ∣ A O O B ∣ = ∣ A C O B ∣ = ∣ A O C B ∣ = ∣ A ∣ ∣ B ∣ \left| \begin{matrix} & {A\quad O} \\ & {O\quad B} \\ \end{matrix} \right| = \left| \begin{matrix} & {A\quad C} \\ & {O\quad B} \\ \end{matrix} \right| = \left| \begin{matrix} & {A\quad O} \\ & {C\quad B} \\ \end{matrix} \right| =| A||B| AOOB = ACOB = AOCB =∣A∣∣B∣
, A , B A,B A,B为方阵,但 ∣ O A m × m B n × n O ∣ = ( − 1 ) m n ∣ A ∣ ∣ B ∣ \left| \begin{matrix} {O} & A_{m \times m} \\ B_{n \times n} & { O} \\ \end{matrix} \right| = ({- 1)}^{{mn}}|A||B| OBn×nAm×mO =(−1)mn∣A∣∣B∣ 。
(6) 范德蒙行列式 D n = ∣ 1 1 … 1 x 1 x 2 … x n … … … … x 1 n − 1 x 2 n 1 … x n n − 1 ∣ = ∏ 1 ≤ j < i ≤ n ( x i − x j ) D_{n} = \begin{vmatrix} 1 & 1 & \ldots & 1 \\ x_{1} & x_{2} & \ldots & x_{n} \\ \ldots & \ldots & \ldots & \ldots \\ x_{1}^{n - 1} & x_{2}^{n 1} & \ldots & x_{n}^{n - 1} \\ \end{vmatrix} = \prod_{1 \leq j < i \leq n}^{}\,(x_{i} - x_{j}) Dn= 1x1…x1n−11x2…x2n1…………1xn…xnn−1 =∏1≤j<i≤n(xi−xj)
设 A A A是 n n n阶方阵, λ i ( i = 1 , 2 ⋯ , n ) \lambda_{i}(i = 1,2\cdots,n) λi(i=1,2⋯,n)是 A A A的 n n n个特征值,则
∣ A ∣ = ∏ i = 1 n λ i |A| = \prod_{i = 1}^{n}\lambda_{i} ∣A∣=∏i=1nλi
矩阵
矩阵: m × n m \times n m×n个数 a i j a_{{ij}} aij排成 m m m行 n n n列的表格 [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ ⋯ a m 1 a m 2 ⋯ a m n ] \begin{bmatrix} a_{11}\quad a_{12}\quad\cdots\quad a_{1n} \\ a_{21}\quad a_{22}\quad\cdots\quad a_{2n} \\ \quad\cdots\cdots\cdots\cdots\cdots \\ a_{m1}\quad a_{m2}\quad\cdots\quad a_{{mn}} \\ \end{bmatrix} a11a12⋯a1na21a22⋯a2n⋯⋯⋯⋯⋯am1am2⋯amn 称为矩阵,简记为 A A A,或者 ( a i j ) m × n \left( a_{{ij}} \right)_{m \times n} (aij)m×n 。若 m = n m = n m=n,则称 A A A是 n n n阶矩阵或 n n n阶方阵。
矩阵的线性运算
1.矩阵的加法
设 A = ( a i j ) , B = ( b i j ) A = (a_{{ij}}),B = (b_{{ij}}) A=(aij),B=(bij)是两个 m × n m \times n m×n矩阵,则 m × n m \times n m×n 矩阵 C = c i j ) = a i j + b i j C = c_{{ij}}) = a_{{ij}} + b_{{ij}} C=cij)=aij+bij称为矩阵 A A A与 B B B的和,记为 A + B = C A + B = C A+B=C 。
2.矩阵的数乘
设 A = ( a i j ) A = (a_{{ij}}) A=(aij)是 m × n m \times n m×n矩阵, k k k是一个常数,则 m × n m \times n m×n矩阵 ( k a i j ) (ka_{{ij}}) (kaij)称为数 k k k与矩阵 A A A的数乘,记为 k A {kA} kA。
3.矩阵的乘法
设 A = ( a i j ) A = (a_{{ij}}) A=(aij)是 m × n m \times n m×n矩阵, B = ( b i j ) B = (b_{{ij}}) B=(bij)是 n × s n \times s n×s矩阵,那么 m × s m \times s m×s矩阵 C = ( c i j ) C = (c_{{ij}}) C=(cij),其中 c i j = a i 1 b 1 j + a i 2 b 2 j + ⋯ + a i n b n j = ∑ k = 1 n a i k b k j c_{{ij}} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{{in}}b_{{nj}} = \sum_{k =1}^{n}{a_{{ik}}b_{{kj}}} cij=ai1b1j+ai2b2j+⋯+ainbnj=∑k=1naikbkj称为 A B {AB} AB的乘积,记为 C = A B C = AB C=AB 。
4. A T \mathbf{A}^{\mathbf{T}} AT、 A − 1 \mathbf{A}^{\mathbf{-1}} A−1、 A ∗ \mathbf{A}^{\mathbf{*}} A∗三者之间的关系
(1) ( A T ) T = A , ( A B ) T = B T A T , ( k A ) T = k A T , ( A ± B ) T = A T ± B T {(A^{T})}^{T} = A,{(AB)}^{T} = B^{T}A^{T},{(kA)}^{T} = kA^{T},{(A \pm B)}^{T} = A^{T} \pm B^{T} (AT)T=A,(AB)T=BTAT,(kA)T=kAT,(A±B)T=AT±BT
(2) ( A − 1 ) − 1 = A , ( A B ) − 1 = B − 1 A − 1 , ( k A ) − 1 = 1 k A − 1 , \left( A^{- 1} \right)^{- 1} = A,\left( {AB} \right)^{- 1} = B^{- 1}A^{- 1},\left( {kA} \right)^{- 1} = \frac{1}{k}A^{- 1}, (A−1)−1=A,(AB)−1=B−1A−1,(kA)−1=k1A−1,
但 ( A ± B ) − 1 = A − 1 ± B − 1 {(A \pm B)}^{- 1} = A^{- 1} \pm B^{- 1} (A±B)−1=A−1±B−1不一定成立。
(3) ( A ∗ ) ∗ = ∣ A ∣ n − 2 A ( n ≥ 3 ) \left( A^{*} \right)^{*} = |A|^{n - 2}\ A\ \ (n \geq 3) (A∗)∗=∣A∣n−2 A (n≥3), ( A B ) ∗ = B ∗ A ∗ , \left({AB} \right)^{*} = B^{*}A^{*}, (AB)∗=B∗A∗, ( k A ) ∗ = k n − 1 A ∗ ( n ≥ 2 ) \left( {kA} \right)^{*} = k^{n -1}A^{*}{\ \ }\left( n \geq 2 \right) (kA)∗=kn−1A∗ (n≥2)
但 ( A ± B ) ∗ = A ∗ ± B ∗ \left( A \pm B \right)^{*} = A^{*} \pm B^{*} (A±B)∗=A∗±B∗不一定成立。
(4) ( A − 1 ) T = ( A T ) − 1 , ( A − 1 ) ∗ = ( A A ∗ ) − 1 , ( A ∗ ) T = ( A T ) ∗ {(A^{- 1})}^{T} = {(A^{T})}^{- 1},\ \left( A^{- 1} \right)^{*} ={(AA^{*})}^{- 1},{(A^{*})}^{T} = \left( A^{T} \right)^{*} (A−1)T=(AT)−1, (A−1)∗=(AA∗)−1,(A∗)T=(AT)∗
5.有关 A ∗ \mathbf{A}^{\mathbf{*}} A∗的结论
(1) A A ∗ = A ∗ A = ∣ A ∣ E AA^{*} = A^{*}A = |A|E AA∗=A∗A=∣A∣E
(2) ∣ A ∗ ∣ = ∣ A ∣ n − 1 ( n ≥ 2 ) , ( k A ) ∗ = k n − 1 A ∗ , ( A ∗ ) ∗ = ∣ A ∣ n − 2 A ( n ≥ 3 ) |A^{*}| = |A|^{n - 1}\ (n \geq 2),\ \ \ \ {(kA)}^{*} = k^{n -1}A^{*},{{\ \ }\left( A^{*} \right)}^{*} = |A|^{n - 2}A(n \geq 3) ∣A∗∣=∣A∣n−1 (n≥2), (kA)∗=kn−1A∗, (A∗)∗=∣A∣n−2A(n≥3)
(3) 若 A A A可逆,则 A ∗ = ∣ A ∣ A − 1 , ( A ∗ ) ∗ = 1 ∣ A ∣ A A^{*} = |A|A^{- 1},{(A^{*})}^{*} = \frac{1}{|A|}A A∗=∣A∣A−1,(A∗)∗=∣A∣1A
(4) 若 A A A为 n n n阶方阵,则:
r ( A ∗ ) = { n , r ( A ) = n 1 , r ( A ) = n − 1 0 , r ( A ) < n − 1 r(A^*)=\begin{cases}n,\quad r(A)=n\\ 1,\quad r(A)=n-1\\ 0,\quad r(A)<n-1\end{cases} r(A∗)=⎩ ⎨ ⎧n,r(A)=n1,r(A)=n−10,r(A)<n−1
6.有关 A − 1 \mathbf{A}^{\mathbf{- 1}} A−1的结论
A A A可逆 ⇔ A B = E ; ⇔ ∣ A ∣ ≠ 0 ; ⇔ r ( A ) = n ; \Leftrightarrow AB = E; \Leftrightarrow |A| \neq 0; \Leftrightarrow r(A) = n; ⇔AB=E;⇔∣A∣=0;⇔r(A)=n;
⇔ A \Leftrightarrow A ⇔A可以表示为初等矩阵的乘积; ⇔ A ; ⇔ A x = 0 \Leftrightarrow A;\Leftrightarrow Ax = 0 ⇔A;⇔Ax=0。
7.有关矩阵秩的结论
(1) 秩 r ( A ) r(A) r(A)=行秩=列秩;
(2) r ( A m × n ) ≤ min ( m , n ) ; r(A_{m \times n}) \leq \min(m,n); r(Am×n)≤min(m,n);
(3) A ≠ 0 ⇒ r ( A ) ≥ 1 A \neq 0 \Rightarrow r(A) \geq 1 A=0⇒r(A)≥1;
(4) r ( A ± B ) ≤ r ( A ) + r ( B ) ; r(A \pm B) \leq r(A) + r(B); r(A±B)≤r(A)+r(B);
(5) 初等变换不改变矩阵的秩
(6) r ( A ) + r ( B ) − n ≤ r ( A B ) ≤ min ( r ( A ) , r ( B ) ) , r(A) + r(B) - n \leq r(AB) \leq \min(r(A),r(B)), r(A)+r(B)−n≤r(AB)≤min(r(A),r(B)),特别若 A B = O AB = O AB=O
则: r ( A ) + r ( B ) ≤ n r(A) + r(B) \leq n r(A)+r(B)≤n
(7) 若 A − 1 A^{- 1} A−1存在 ⇒ r ( A B ) = r ( B ) ; \Rightarrow r(AB) = r(B); ⇒r(AB)=r(B); 若 B − 1 B^{- 1} B−1存在
⇒ r ( A B ) = r ( A ) ; \Rightarrow r(AB) = r(A); ⇒r(AB)=r(A);
若 r ( A m × n ) = n ⇒ r ( A B ) = r ( B ) ; r(A_{m \times n}) = n \Rightarrow r(AB) = r(B); r(Am×n)=n⇒r(AB)=r(B); 若 r ( A m × s ) = n ⇒ r ( A B ) = r ( A ) r(A_{m \times s}) = n\Rightarrow r(AB) = r\left( A \right) r(Am×s)=n⇒r(AB)=r(A)。
(8) r ( A m × s ) = n ⇔ A x = 0 r(A_{m \times s}) = n \Leftrightarrow Ax = 0 r(Am×s)=n⇔Ax=0只有零解
8.分块求逆公式
( A O O B ) − 1 = ( A − 1 O O B − 1 ) \begin{pmatrix} A & O \\ O & B \\ \end{pmatrix}^{- 1} = \begin{pmatrix} A^{-1} & O \\ O & B^{- 1} \\ \end{pmatrix} (AOOB)−1=(A−1OOB−1); ( A C O B ) − 1 = ( A − 1 − A − 1 C B − 1 O B − 1 ) \begin{pmatrix} A & C \\ O & B \\\end{pmatrix}^{- 1} = \begin{pmatrix} A^{- 1}& - A^{- 1}CB^{- 1} \\ O & B^{- 1} \\ \end{pmatrix} (AOCB)−1=(A−1O−A−1CB−1B−1);
( A O C B ) − 1 = ( A − 1 O − B − 1 C A − 1 B − 1 ) \begin{pmatrix} A & O \\ C & B \\ \end{pmatrix}^{- 1} = \begin{pmatrix} A^{- 1}&{O} \\ - B^{- 1}CA^{- 1} & B^{- 1} \\\end{pmatrix} (ACOB)−1=(A−1−B−1CA−1OB−1); ( O A B O ) − 1 = ( O B − 1 A − 1 O ) \begin{pmatrix} O & A \\ B & O \\ \end{pmatrix}^{- 1} =\begin{pmatrix} O & B^{- 1} \\ A^{- 1} & O \\ \end{pmatrix} (OBAO)−1=(OA−1B−1O)
这里 A A A, B B B均为可逆方阵。
向量
1.有关向量组的线性表示
(1) α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs线性相关 ⇔ \Leftrightarrow ⇔至少有一个向量可以用其余向量线性表示。
(2) α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs线性无关, α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs, β \beta β线性相关 ⇔ β \Leftrightarrow \beta ⇔β可以由 α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs唯一线性表示。
(3) β \beta β可以由 α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs线性表示
⇔ r ( α 1 , α 2 , ⋯ , α s ) = r ( α 1 , α 2 , ⋯ , α s , β ) \Leftrightarrow r(\alpha_{1},\alpha_{2},\cdots,\alpha_{s}) =r(\alpha_{1},\alpha_{2},\cdots,\alpha_{s},\beta) ⇔r(α1,α2,⋯,αs)=r(α1,α2,⋯,αs,β) 。
2.有关向量组的线性相关性
(1)部分相关,整体相关;整体无关,部分无关.
(2) ① n n n个 n n n维向量
α 1 , α 2 ⋯ α n \alpha_{1},\alpha_{2}\cdots\alpha_{n} α1,α2⋯αn线性无关 ⇔ ∣ [ α 1 α 2 ⋯ α n ] ∣ ≠ 0 \Leftrightarrow \left|\left\lbrack \alpha_{1}\alpha_{2}\cdots\alpha_{n} \right\rbrack \right| \neq0 ⇔∣[α1α2⋯αn]∣=0, n n n个 n n n维向量 α 1 , α 2 ⋯ α n \alpha_{1},\alpha_{2}\cdots\alpha_{n} α1,α2⋯αn线性相关
⇔ ∣ [ α 1 , α 2 , ⋯ , α n ] ∣ = 0 \Leftrightarrow |\lbrack\alpha_{1},\alpha_{2},\cdots,\alpha_{n}\rbrack| = 0 ⇔∣[α1,α2,⋯,αn]∣=0
。
② n + 1 n + 1 n+1个 n n n维向量线性相关。
③ 若 α 1 , α 2 ⋯ α S \alpha_{1},\alpha_{2}\cdots\alpha_{S} α1,α2⋯αS线性无关,则添加分量后仍线性无关;或一组向量线性相关,去掉某些分量后仍线性相关。
3.有关向量组的线性表示
(1) α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs线性相关 ⇔ \Leftrightarrow ⇔至少有一个向量可以用其余向量线性表示。
(2) α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs线性无关, α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs, β \beta β线性相关 ⇔ β \Leftrightarrow\beta ⇔β 可以由 α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs唯一线性表示。
(3) β \beta β可以由 α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs线性表示
⇔ r ( α 1 , α 2 , ⋯ , α s ) = r ( α 1 , α 2 , ⋯ , α s , β ) \Leftrightarrow r(\alpha_{1},\alpha_{2},\cdots,\alpha_{s}) =r(\alpha_{1},\alpha_{2},\cdots,\alpha_{s},\beta) ⇔r(α1,α2,⋯,αs)=r(α1,α2,⋯,αs,β)
4.向量组的秩与矩阵的秩之间的关系
设 r ( A m × n ) = r r(A_{m \times n}) =r r(Am×n)=r,则 A A A的秩 r ( A ) r(A) r(A)与 A A A的行列向量组的线性相关性关系为:
(1) 若 r ( A m × n ) = r = m r(A_{m \times n}) = r = m r(Am×n)=r=m,则 A A A的行向量组线性无关。
(2) 若 r ( A m × n ) = r < m r(A_{m \times n}) = r < m r(Am×n)=r<m,则 A A A的行向量组线性相关。
(3) 若 r ( A m × n ) = r = n r(A_{m \times n}) = r = n r(Am×n)=r=n,则 A A A的列向量组线性无关。
(4) 若 r ( A m × n ) = r < n r(A_{m \times n}) = r < n r(Am×n)=r<n,则 A A A的列向量组线性相关。
5. n \mathbf{n} n维向量空间的基变换公式及过渡矩阵
若 α 1 , α 2 , ⋯ , α n \alpha_{1},\alpha_{2},\cdots,\alpha_{n} α1,α2,⋯,αn与 β 1 , β 2 , ⋯ , β n \beta_{1},\beta_{2},\cdots,\beta_{n} β1,β2,⋯,βn是向量空间 V V V的两组基,则基变换公式为:
( β 1 , β 2 , ⋯ , β n ) = ( α 1 , α 2 , ⋯ , α n ) [ c 11 c 12 ⋯ c 1 n c 21 c 22 ⋯ c 2 n ⋯ ⋯ ⋯ ⋯ c n 1 c n 2 ⋯ c n n ] = ( α 1 , α 2 , ⋯ , α n ) C (\beta_{1},\beta_{2},\cdots,\beta_{n}) = (\alpha_{1},\alpha_{2},\cdots,\alpha_{n})\begin{bmatrix} c_{11}& c_{12}& \cdots & c_{1n} \\ c_{21}& c_{22}&\cdots & c_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ c_{n1}& c_{n2} & \cdots & c_{{nn}} \\\end{bmatrix} = (\alpha_{1},\alpha_{2},\cdots,\alpha_{n})C (β1,β2,⋯,βn)=(α1,α2,⋯,αn) c11c21⋯cn1c12c22⋯cn2⋯⋯⋯⋯c1nc2n⋯cnn =(α1,α2,⋯,αn)C
其中 C C C是可逆矩阵,称为由基 α 1 , α 2 , ⋯ , α n \alpha_{1},\alpha_{2},\cdots,\alpha_{n} α1,α2,⋯,αn到基 β 1 , β 2 , ⋯ , β n \beta_{1},\beta_{2},\cdots,\beta_{n} β1,β2,⋯,βn的过渡矩阵。
6.坐标变换公式
若向量 γ \gamma γ在基 α 1 , α 2 , ⋯ , α n \alpha_{1},\alpha_{2},\cdots,\alpha_{n} α1,α2,⋯,αn与基 β 1 , β 2 , ⋯ , β n \beta_{1},\beta_{2},\cdots,\beta_{n} β1,β2,⋯,βn的坐标分别是
X = ( x 1 , x 2 , ⋯ , x n ) T X = {(x_{1},x_{2},\cdots,x_{n})}^{T} X=(x1,x2,⋯,xn)T,
Y = ( y 1 , y 2 , ⋯ , y n ) T Y = \left( y_{1},y_{2},\cdots,y_{n} \right)^{T} Y=(y1,y2,⋯,yn)T 即: γ = x 1 α 1 + x 2 α 2 + ⋯ + x n α n = y 1 β 1 + y 2 β 2 + ⋯ + y n β n \gamma =x_{1}\alpha_{1} + x_{2}\alpha_{2} + \cdots + x_{n}\alpha_{n} = y_{1}\beta_{1} +y_{2}\beta_{2} + \cdots + y_{n}\beta_{n} γ=x1α1+x2α2+⋯+xnαn=y1β1+y2β2+⋯+ynβn,则向量坐标变换公式为 X = C Y X = CY X=CY 或 Y = C − 1 X Y = C^{- 1}X Y=C−1X,其中 C C C是从基 α 1 , α 2 , ⋯ , α n \alpha_{1},\alpha_{2},\cdots,\alpha_{n} α1,α2,⋯,αn到基 β 1 , β 2 , ⋯ , β n \beta_{1},\beta_{2},\cdots,\beta_{n} β1,β2,⋯,βn的过渡矩阵。
7.向量的内积
( α , β ) = a 1 b 1 + a 2 b 2 + ⋯ + a n b n = α T β = β T α (\alpha,\beta) = a_{1}b_{1} + a_{2}b_{2} + \cdots + a_{n}b_{n} = \alpha^{T}\beta = \beta^{T}\alpha (α,β)=a1b1+a2b2+⋯+anbn=αTβ=βTα
8.Schmidt 正交化
若 α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs线性无关,则可构造 β 1 , β 2 , ⋯ , β s \beta_{1},\beta_{2},\cdots,\beta_{s} β1,β2,⋯,βs使其两两正交,且 β i \beta_{i} βi仅是 α 1 , α 2 , ⋯ , α i \alpha_{1},\alpha_{2},\cdots,\alpha_{i} α1,α2,⋯,αi的线性组合 ( i = 1 , 2 , ⋯ , n ) (i= 1,2,\cdots,n) (i=1,2,⋯,n),再把 β i \beta_{i} βi单位化,记 γ i = β i ∣ β i ∣ \gamma_{i} =\frac{\beta_{i}}{\left| \beta_{i}\right|} γi=∣βi∣βi,则 γ 1 , γ 2 , ⋯ , γ i \gamma_{1},\gamma_{2},\cdots,\gamma_{i} γ1,γ2,⋯,γi是规范正交向量组。其中
β 1 = α 1 \beta_{1} = \alpha_{1} β1=α1, β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 \beta_{2} = \alpha_{2} -\frac{(\alpha_{2},\beta_{1})}{(\beta_{1},\beta_{1})}\beta_{1} β2=α2−(β1,β1)(α2,β1)β1 , β 3 = α 3 − ( α 3 , β 1 ) ( β 1 , β 1 ) β 1 − ( α 3 , β 2 ) ( β 2 , β 2 ) β 2 \beta_{3} =\alpha_{3} - \frac{(\alpha_{3},\beta_{1})}{(\beta_{1},\beta_{1})}\beta_{1} -\frac{(\alpha_{3},\beta_{2})}{(\beta_{2},\beta_{2})}\beta_{2} β3=α3−(β1,β1)(α3,β1)β1−(β2,β2)(α3,β2)β2 ,
…
β s = α s − ( α s , β 1 ) ( β 1 , β 1 ) β 1 − ( α s , β 2 ) ( β 2 , β 2 ) β 2 − ⋯ − ( α s , β s − 1 ) ( β s − 1 , β s − 1 ) β s − 1 \beta_{s} = \alpha_{s} - \frac{(\alpha_{s},\beta_{1})}{(\beta_{1},\beta_{1})}\beta_{1} - \frac{(\alpha_{s},\beta_{2})}{(\beta_{2},\beta_{2})}\beta_{2} - \cdots - \frac{(\alpha_{s},\beta_{s - 1})}{(\beta_{s - 1},\beta_{s - 1})}\beta_{s - 1} βs=αs−(β1,β1)(αs,β1)β1−(β2,β2)(αs,β2)β2−⋯−(βs−1,βs−1)(αs,βs−1)βs−1
9.正交基及规范正交基
向量空间一组基中的向量如果两两正交,就称为正交基;若正交基中每个向量都是单位向量,就称其为规范正交基。
线性方程组
1.克莱姆法则
线性方程组 { a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = b n \begin{cases} a_{11}x_{1} + a_{12}x_{2} + \cdots +a_{1n}x_{n} = b_{1} \\ a_{21}x_{1} + a_{22}x_{2} + \cdots + a_{2n}x_{n} =b_{2} \\ \quad\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots \\ a_{n1}x_{1} + a_{n2}x_{2} + \cdots + a_{{nn}}x_{n} = b_{n} \\ \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯⋯⋯⋯⋯⋯⋯an1x1+an2x2+⋯+annxn=bn,如果系数行列式 D = ∣ A ∣ ≠ 0 D = \left| A \right| \neq 0 D=∣A∣=0,则方程组有唯一解, x 1 = D 1 D , x 2 = D 2 D , ⋯ , x n = D n D x_{1} = \frac{D_{1}}{D},x_{2} = \frac{D_{2}}{D},\cdots,x_{n} =\frac{D_{n}}{D} x1=DD1,x2=DD2,⋯,xn=DDn,其中 D j D_{j} Dj是把 D D D中第 j j j列元素换成方程组右端的常数列所得的行列式。
2. n n n阶矩阵 A A A可逆 ⇔ A x = 0 \Leftrightarrow Ax = 0 ⇔Ax=0只有零解。 ⇔ ∀ b , A x = b \Leftrightarrow\forall b,Ax = b ⇔∀b,Ax=b总有唯一解,一般地, r ( A m × n ) = n ⇔ A x = 0 r(A_{m \times n}) = n \Leftrightarrow Ax= 0 r(Am×n)=n⇔Ax=0只有零解。
3.非奇次线性方程组有解的充分必要条件,线性方程组解的性质和解的结构
(1) 设 A A A为 m × n m \times n m×n矩阵,若 r ( A m × n ) = m r(A_{m \times n}) = m r(Am×n)=m,则对 A x = b Ax =b Ax=b而言必有 r ( A ) = r ( A ⋮ b ) = m r(A) = r(A \vdots b) = m r(A)=r(A⋮b)=m,从而 A x = b Ax = b Ax=b有解。
(2) 设 x 1 , x 2 , ⋯ x s x_{1},x_{2},\cdots x_{s} x1,x2,⋯xs为 A x = b Ax = b Ax=b的解,则 k 1 x 1 + k 2 x 2 ⋯ + k s x s k_{1}x_{1} + k_{2}x_{2}\cdots + k_{s}x_{s} k1x1+k2x2⋯+ksxs当 k 1 + k 2 + ⋯ + k s = 1 k_{1} + k_{2} + \cdots + k_{s} = 1 k1+k2+⋯+ks=1时仍为 A x = b Ax =b Ax=b的解;但当 k 1 + k 2 + ⋯ + k s = 0 k_{1} + k_{2} + \cdots + k_{s} = 0 k1+k2+⋯+ks=0时,则为 A x = 0 Ax =0 Ax=0的解。特别 x 1 + x 2 2 \frac{x_{1} + x_{2}}{2} 2x1+x2为 A x = b Ax = b Ax=b的解; 2 x 3 − ( x 1 + x 2 ) 2x_{3} - (x_{1} +x_{2}) 2x3−(x1+x2)为 A x = 0 Ax = 0 Ax=0的解。
(3) 非齐次线性方程组 A x = b {Ax} = b Ax=b无解 ⇔ r ( A ) + 1 = r ( A ‾ ) ⇔ b \Leftrightarrow r(A) + 1 =r(\overline{A}) \Leftrightarrow b ⇔r(A)+1=r(A)⇔b不能由 A A A的列向量 α 1 , α 2 , ⋯ , α n \alpha_{1},\alpha_{2},\cdots,\alpha_{n} α1,α2,⋯,αn线性表示。
4.奇次线性方程组的基础解系和通解,解空间,非奇次线性方程组的通解
(1) 齐次方程组 A x = 0 {Ax} = 0 Ax=0恒有解(必有零解)。当有非零解时,由于解向量的任意线性组合仍是该齐次方程组的解向量,因此 A x = 0 {Ax}= 0 Ax=0的全体解向量构成一个向量空间,称为该方程组的解空间,解空间的维数是 n − r ( A ) n - r(A) n−r(A),解空间的一组基称为齐次方程组的基础解系。
(2) η 1 , η 2 , ⋯ , η t \eta_{1},\eta_{2},\cdots,\eta_{t} η1,η2,⋯,ηt是 A x = 0 {Ax} = 0 Ax=0的基础解系,即:
-
η 1 , η 2 , ⋯ , η t \eta_{1},\eta_{2},\cdots,\eta_{t} η1,η2,⋯,ηt是 A x = 0 {Ax} = 0 Ax=0的解;
-
η 1 , η 2 , ⋯ , η t \eta_{1},\eta_{2},\cdots,\eta_{t} η1,η2,⋯,ηt线性无关;
-
A x = 0 {Ax} = 0 Ax=0的任一解都可以由 η 1 , η 2 , ⋯ , η t \eta_{1},\eta_{2},\cdots,\eta_{t} η1,η2,⋯,ηt线性表出.
k 1 η 1 + k 2 η 2 + ⋯ + k t η t k_{1}\eta_{1} + k_{2}\eta_{2} + \cdots + k_{t}\eta_{t} k1η1+k2η2+⋯+ktηt是 A x = 0 {Ax} = 0 Ax=0的通解,其中 k 1 , k 2 , ⋯ , k t k_{1},k_{2},\cdots,k_{t} k1,k2,⋯,kt是任意常数。
矩阵的特征值和特征向量
1.矩阵的特征值和特征向量的概念及性质
(1) 设 λ \lambda λ是 A A A的一个特征值,则 k A , a A + b E , A 2 , A m , f ( A ) , A T , A − 1 , A ∗ {kA},{aA} + {bE},A^{2},A^{m},f(A),A^{T},A^{- 1},A^{*} kA,aA+bE,A2,Am,f(A),AT,A−1,A∗有一个特征值分别为
k λ , a λ + b , λ 2 , λ m , f ( λ ) , λ , λ − 1 , ∣ A ∣ λ , {kλ},{aλ} + b,\lambda^{2},\lambda^{m},f(\lambda),\lambda,\lambda^{- 1},\frac{|A|}{\lambda}, kλ,aλ+b,λ2,λm,f(λ),λ,λ−1,λ∣A∣,且对应特征向量相同( A T A^{T} AT 例外)。
(2)若 λ 1 , λ 2 , ⋯ , λ n \lambda_{1},\lambda_{2},\cdots,\lambda_{n} λ1,λ2,⋯,λn为 A A A的 n n n个特征值,则 ∑ i = 1 n λ i = ∑ i = 1 n a i i , ∏ i = 1 n λ i = ∣ A ∣ \sum_{i= 1}^{n}\lambda_{i} = \sum_{i = 1}^{n}a_{{ii}},\prod_{i = 1}^{n}\lambda_{i}= |A| ∑i=1nλi=∑i=1naii,∏i=1nλi=∣A∣ ,从而 ∣ A ∣ ≠ 0 ⇔ A |A| \neq 0 \Leftrightarrow A ∣A∣=0⇔A没有特征值。
(3)设 λ 1 , λ 2 , ⋯ , λ s \lambda_{1},\lambda_{2},\cdots,\lambda_{s} λ1,λ2,⋯,λs为 A A A的 s s s个特征值,对应特征向量为 α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs,
若: α = k 1 α 1 + k 2 α 2 + ⋯ + k s α s \alpha = k_{1}\alpha_{1} + k_{2}\alpha_{2} + \cdots + k_{s}\alpha_{s} α=k1α1+k2α2+⋯+ksαs ,
则: A n α = k 1 A n α 1 + k 2 A n α 2 + ⋯ + k s A n α s = k 1 λ 1 n α 1 + k 2 λ 2 n α 2 + ⋯ k s λ s n α s A^{n}\alpha = k_{1}A^{n}\alpha_{1} + k_{2}A^{n}\alpha_{2} + \cdots +k_{s}A^{n}\alpha_{s} = k_{1}\lambda_{1}^{n}\alpha_{1} +k_{2}\lambda_{2}^{n}\alpha_{2} + \cdots k_{s}\lambda_{s}^{n}\alpha_{s} Anα=k1Anα1+k2Anα2+⋯+ksAnαs=k1λ1nα1+k2λ2nα2+⋯ksλsnαs 。
2.相似变换、相似矩阵的概念及性质
(1) 若 A ∼ B A \sim B A∼B,则
-
A T ∼ B T , A − 1 ∼ B − 1 , , A ∗ ∼ B ∗ A^{T} \sim B^{T},A^{- 1} \sim B^{- 1},,A^{*} \sim B^{*} AT∼BT,A−1∼B−1,,A∗∼B∗
-
∣ A ∣ = ∣ B ∣ , ∑ i = 1 n A i i = ∑ i = 1 n b i i , r ( A ) = r ( B ) |A| = |B|,\sum_{i = 1}^{n}A_{{ii}} = \sum_{i =1}^{n}b_{{ii}},r(A) = r(B) ∣A∣=∣B∣,∑i=1nAii=∑i=1nbii,r(A)=r(B)
-
∣ λ E − A ∣ = ∣ λ E − B ∣ |\lambda E - A| = |\lambda E - B| ∣λE−A∣=∣λE−B∣,对 ∀ λ \forall\lambda ∀λ成立
3.矩阵可相似对角化的充分必要条件
(1)设 A A A为 n n n阶方阵,则 A A A可对角化 ⇔ \Leftrightarrow ⇔对每个 k i k_{i} ki重根特征值 λ i \lambda_{i} λi,有 n − r ( λ i E − A ) = k i n-r(\lambda_{i}E - A) = k_{i} n−r(λiE−A)=ki
(2) 设 A A A可对角化,则由 P − 1 A P = Λ , P^{- 1}{AP} = \Lambda, P−1AP=Λ,有 A = P Λ P − 1 A = {PΛ}P^{-1} A=PΛP−1,从而 A n = P Λ n P − 1 A^{n} = P\Lambda^{n}P^{- 1} An=PΛnP−1
(3) 重要结论
-
若 A ∼ B , C ∼ D A \sim B,C \sim D A∼B,C∼D,则 [ A O O C ] ∼ [ B O O D ] \begin{bmatrix} A & O \\ O & C \\\end{bmatrix} \sim \begin{bmatrix} B & O \\ O & D \\\end{bmatrix} [AOOC]∼[BOOD].
-
若 A ∼ B A \sim B A∼B,则 f ( A ) ∼ f ( B ) , ∣ f ( A ) ∣ ∼ ∣ f ( B ) ∣ f(A) \sim f(B),\left| f(A) \right| \sim \left| f(B)\right| f(A)∼f(B),∣f(A)∣∼∣f(B)∣,其中 f ( A ) f(A) f(A)为关于 n n n阶方阵 A A A的多项式。
-
若 A A A为可对角化矩阵,则其非零特征值的个数(重根重复计算)=秩( A A A)
4.实对称矩阵的特征值、特征向量及相似对角阵
(1)相似矩阵:设 A , B A,B A,B为两个 n n n阶方阵,如果存在一个可逆矩阵 P P P,使得 B = P − 1 A P B =P^{- 1}{AP} B=P−1AP成立,则称矩阵 A A A与 B B B相似,记为 A ∼ B A \sim B A∼B。
(2)相似矩阵的性质:如果 A ∼ B A \sim B A∼B则有:
-
A T ∼ B T A^{T} \sim B^{T} AT∼BT
-
A − 1 ∼ B − 1 A^{- 1} \sim B^{- 1} A−1∼B−1 (若 A A A, B B B均可逆)
-
A k ∼ B k A^{k} \sim B^{k} Ak∼Bk ( k k k为正整数)
-
∣ λ E − A ∣ = ∣ λ E − B ∣ \left| {λE} - A \right| = \left| {λE} - B \right| ∣λE−A∣=∣λE−B∣,从而 A , B A,B A,B
有相同的特征值 -
∣ A ∣ = ∣ B ∣ \left| A \right| = \left| B \right| ∣A∣=∣B∣,从而 A , B A,B A,B同时可逆或者不可逆
-
秩 ( A ) = \left( A \right) = (A)=秩 ( B ) , ∣ λ E − A ∣ = ∣ λ E − B ∣ \left( B \right),\left| {λE} - A \right| =\left| {λE} - B \right| (B),∣λE−A∣=∣λE−B∣, A , B A,B A,B不一定相似
二次型
1. n \mathbf{n} n个变量 x 1 , x 2 , ⋯ , x n \mathbf{x}_{\mathbf{1}}\mathbf{,}\mathbf{x}_{\mathbf{2}}\mathbf{,\cdots,}\mathbf{x}_{\mathbf{n}} x1,x2,⋯,xn的二次齐次函数
f ( x 1 , x 2 , ⋯ , x n ) = ∑ i = 1 n ∑ j = 1 n a i j x i y j f(x_{1},x_{2},\cdots,x_{n}) = \sum_{i = 1}^{n}{\sum_{j =1}^{n}{a_{{ij}}x_{i}y_{j}}} f(x1,x2,⋯,xn)=∑i=1n∑j=1naijxiyj,其中 a i j = a j i ( i , j = 1 , 2 , ⋯ , n ) a_{{ij}} = a_{{ji}}(i,j =1,2,\cdots,n) aij=aji(i,j=1,2,⋯,n),称为 n n n元二次型,简称二次型. 若令 x = [ x 1 x 1 ⋮ x n ] , A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a n 1 a n 2 ⋯ a n n ] x = \ \begin{bmatrix}x_{1} \\ x_{1} \\ \vdots \\ x_{n} \\ \end{bmatrix},A = \begin{bmatrix} a_{11}& a_{12}& \cdots & a_{1n} \\ a_{21}& a_{22}& \cdots & a_{2n} \\ \cdots &\cdots &\cdots &\cdots \\ a_{n1}& a_{n2} & \cdots & a_{{nn}} \\\end{bmatrix} x= x1x1⋮xn ,A= a11a21⋯an1a12a22⋯an2⋯⋯⋯⋯a1na2n⋯ann ,这二次型 f f f可改写成矩阵向量形式 f = x T A x f =x^{T}{Ax} f=xTAx。其中 A A A称为二次型矩阵,因为 a i j = a j i ( i , j = 1 , 2 , ⋯ , n ) a_{{ij}} =a_{{ji}}(i,j =1,2,\cdots,n) aij=aji(i,j=1,2,⋯,n),所以二次型矩阵均为对称矩阵,且二次型与对称矩阵一一对应,并把矩阵 A A A的秩称为二次型的秩。
2.惯性定理,二次型的标准形和规范形
(1) 惯性定理
对于任一二次型,不论选取怎样的合同变换使它化为仅含平方项的标准型,其正负惯性指数与所选变换无关,这就是所谓的惯性定理。
(2) 标准形
二次型 f = ( x 1 , x 2 , ⋯ , x n ) = x T A x f = \left( x_{1},x_{2},\cdots,x_{n} \right) =x^{T}{Ax} f=(x1,x2,⋯,xn)=xTAx经过合同变换 x = C y x = {Cy} x=Cy化为 f = x T A x = y T C T A C f = x^{T}{Ax} =y^{T}C^{T}{AC} f=xTAx=yTCTAC
y = ∑ i = 1 r d i y i 2 y = \sum_{i = 1}^{r}{d_{i}y_{i}^{2}} y=∑i=1rdiyi2称为 f ( r ≤ n ) f(r \leq n) f(r≤n)的标准形。在一般的数域内,二次型的标准形不是唯一的,与所作的合同变换有关,但系数不为零的平方项的个数由 r ( A ) r(A) r(A)唯一确定。
(3) 规范形
任一实二次型 f f f都可经过合同变换化为规范形 f = z 1 2 + z 2 2 + ⋯ z p 2 − z p + 1 2 − ⋯ − z r 2 f = z_{1}^{2} + z_{2}^{2} + \cdots z_{p}^{2} - z_{p + 1}^{2} - \cdots -z_{r}^{2} f=z12+z22+⋯zp2−zp+12−⋯−zr2,其中 r r r为 A A A的秩, p p p为正惯性指数, r − p r -p r−p为负惯性指数,且规范型唯一。
3.用正交变换和配方法化二次型为标准形,二次型及其矩阵的正定性
设 A A A正定 ⇒ k A ( k > 0 ) , A T , A − 1 , A ∗ \Rightarrow {kA}(k > 0),A^{T},A^{- 1},A^{*} ⇒kA(k>0),AT,A−1,A∗正定; ∣ A ∣ > 0 |A| >0 ∣A∣>0, A A A可逆; a i i > 0 a_{{ii}} > 0 aii>0,且 ∣ A i i ∣ > 0 |A_{{ii}}| > 0 ∣Aii∣>0
A A A, B B B正定 ⇒ A + B \Rightarrow A +B ⇒A+B正定,但 A B {AB} AB, B A {BA} BA不一定正定
A A A正定 ⇔ f ( x ) = x T A x > 0 , ∀ x ≠ 0 \Leftrightarrow f(x) = x^{T}{Ax} > 0,\forall x \neq 0 ⇔f(x)=xTAx>0,∀x=0
⇔ A \Leftrightarrow A ⇔A的各阶顺序主子式全大于零
⇔ A \Leftrightarrow A ⇔A的所有特征值大于零
⇔ A \Leftrightarrow A ⇔A的正惯性指数为 n n n
⇔ \Leftrightarrow ⇔存在可逆阵 P P P使 A = P T P A = P^{T}P A=PTP
⇔ \Leftrightarrow ⇔存在正交矩阵 Q Q Q,使 Q T A Q = Q − 1 A Q = ( λ 1 ⋱ λ n ) , Q^{T}{AQ} = Q^{- 1}{AQ} =\begin{pmatrix} \lambda_{1} & & \\ \begin{matrix} & \\ & \\ \end{matrix} &\ddots & \\ & & \lambda_{n} \\ \end{pmatrix}, QTAQ=Q−1AQ= λ1⋱λn ,
其中 λ i > 0 , i = 1 , 2 , ⋯ , n . \lambda_{i} > 0,i = 1,2,\cdots,n. λi>0,i=1,2,⋯,n.正定 ⇒ k A ( k > 0 ) , A T , A − 1 , A ∗ \Rightarrow {kA}(k >0),A^{T},A^{- 1},A^{*} ⇒kA(k>0),AT,A−1,A∗正定; ∣ A ∣ > 0 , A |A| > 0,A ∣A∣>0,A可逆; a i i > 0 a_{{ii}} >0 aii>0,且 ∣ A i i ∣ > 0 |A_{{ii}}| > 0 ∣Aii∣>0 。
总体框架
运算性质
参考文章
机器学习的线性代数基础概念 · 机器学习数学基础 (itdiffer.com)
机器学习中的线性代数 - 知乎 (zhihu.com)
线性代数基本知识-思维导图_线性代数思维导图_Arrow的博客-CSDN博客
推荐阅读
【机器学习的数学基础】(一)线性代数(Linear Algebra)(上)_linear algebra for everyone csdn_二进制人工智能的博客-CSDN博客
【机器学习的数学基础】(二)线性代数(Linear Algebra)(中)_二进制人工智能的博客-CSDN博客
【机器学习的数学基础】(三)线性代数(Linear Algebra)(下)_ordered basis线代_二进制人工智能的博客-CSDN博客
考研线性代数最全知识点梳理思维导图 - 知乎 (zhihu.com)
LQLab: Coding Learning Writing — LQLab
本文由博客一文多发平台 OpenWrite 发布!
相关文章:

线性代数 | 机器学习数学基础
前言 线性代数(linear algebra)是关于向量空间和线性映射的一个数学分支。它包括对线、面和子空间的研究,同时也涉及到所有的向量空间的一般性质。 本文主要介绍机器学习中所用到的线性代数核心基础概念,供读者学习阶段查漏补缺…...
Nios初体验之——Hello world!
文章目录 前言一、系统设计1、系统模块框图2、系统涉及到的模块1、时钟2、nios2_qsys3、片内存储(onchip_rom、onchip_ram)4、串行通信(jtag_uart)5、System ID(sysid_qsys) 二、硬件设计1、创建Qsys2、重命…...

[Linux]理解文件系统!动静态库详细制作使用!(缓冲区、inode、软硬链接、动静态库)
hello,大家好,这里是bang___bang_,今天来谈谈的文件系统知识,包含有缓冲区、inode、软硬链接、动静态库。本篇旨在分享记录知识,如有需要,希望能有所帮助。 目录 1️⃣缓冲区 🍙缓冲区的意义 …...
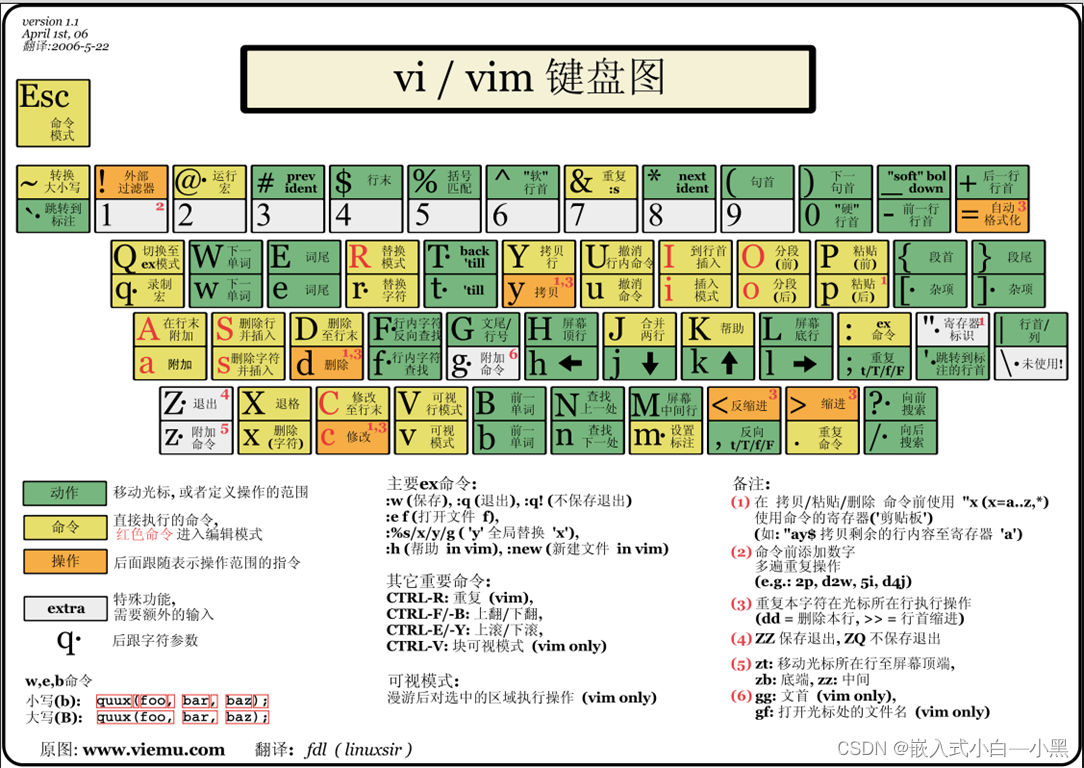
【Linux操作系统】Vim:提升你的编辑效率
Vim是一款功能强大的文本编辑器,它具有高度可定制性和灵活性,可以帮助程序员和文本编辑者提高编辑效率。本文将介绍Vim的基本使用方法、常用功能和一些实用技巧。 文章目录 1. Vim的基本使用方法:2. 常用功能:2.1 文件操作&#…...
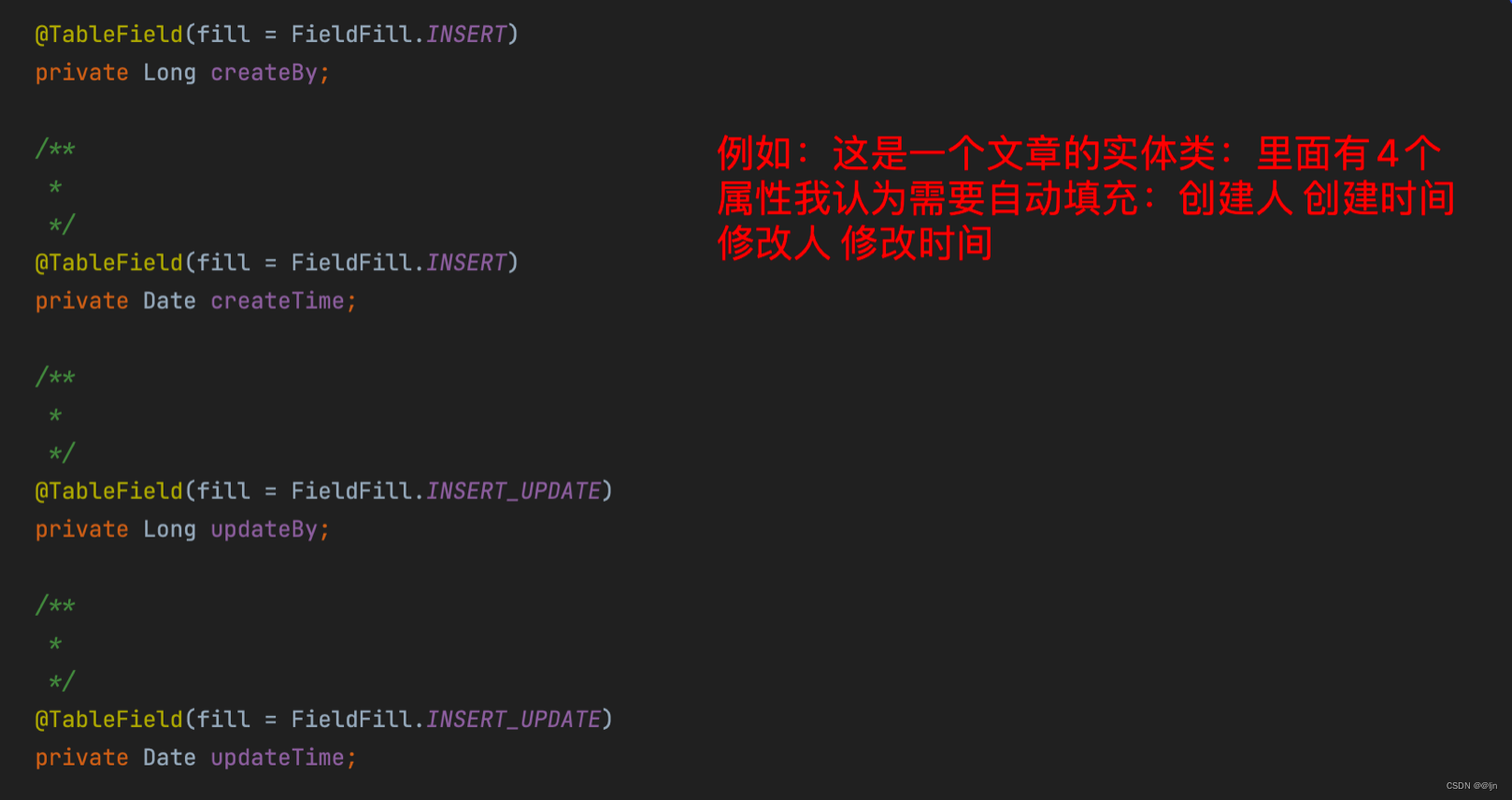
Mybatis-plus 的自动填充策略
当在项目中需要对某些实体类中的公共的属性进行自动填充时,可以使用Mybatis-plus中的自动填充功能。 (1)我们可以在实体类中把要自动填充的类属性加上指定的注解TableField(填写在上面方法时进行填充的枚举类型填充策略ÿ…...
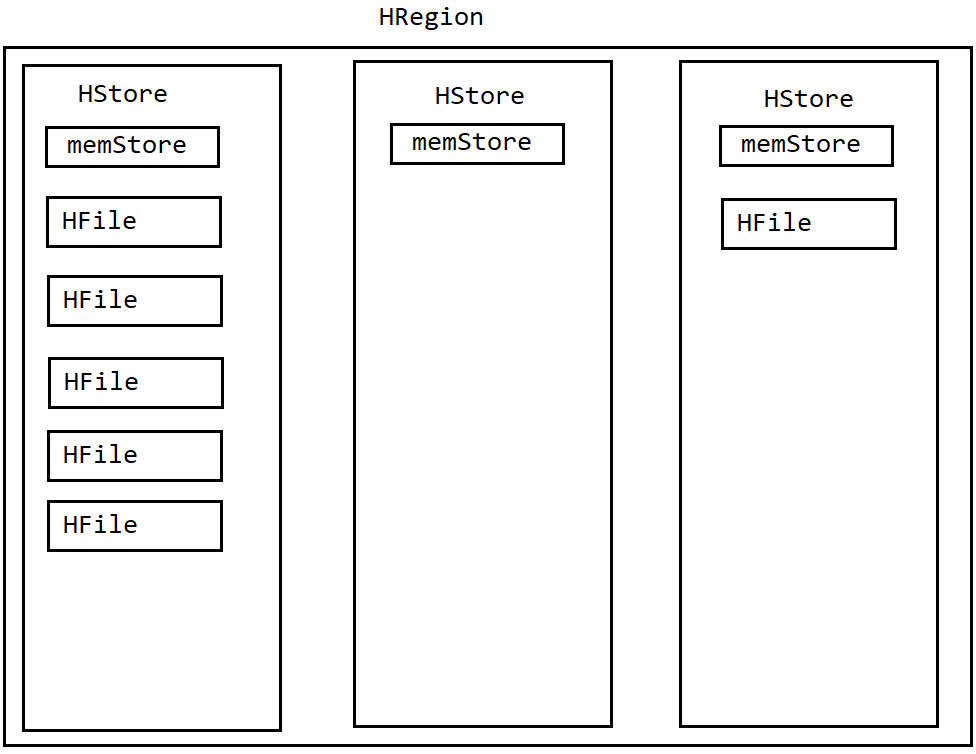
大数据课程G2——Hbase的基本架构
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握Hbase的基本架构; ⚪ 掌握Hbase的读写流程; ⚪ 掌握Hbase的设计与优化; 一、基本架构 1. HRegion 1. 在HBase中,会将一个表从行键方向上进行切分,切分成1个或者多个HRegion。 …...
微信小程序wx.getlocation接口权限申请总结
先附上申请通过截图 插播内容:可代开通,保证通过。wx.getLocation接口(获取当前的地址位置) qq: 308205428 如何申请 当申请微信小程序的wx.getLocation接口权限时,你可以…...

简单游戏截图_可控截取内容1
一个需求 我需要在场景中截取不同层级的截图(如只截模型或只截UI或只截外部相加看到的画面 或全都截或和Shader配合呈现人眼夜视仪热成像的画面切换) 将截图排到列表中,在场景UI中展示出来 如何做 相机要能够看到不同的画面 将当前帧画面存储下来 将存储的画面展示出…...
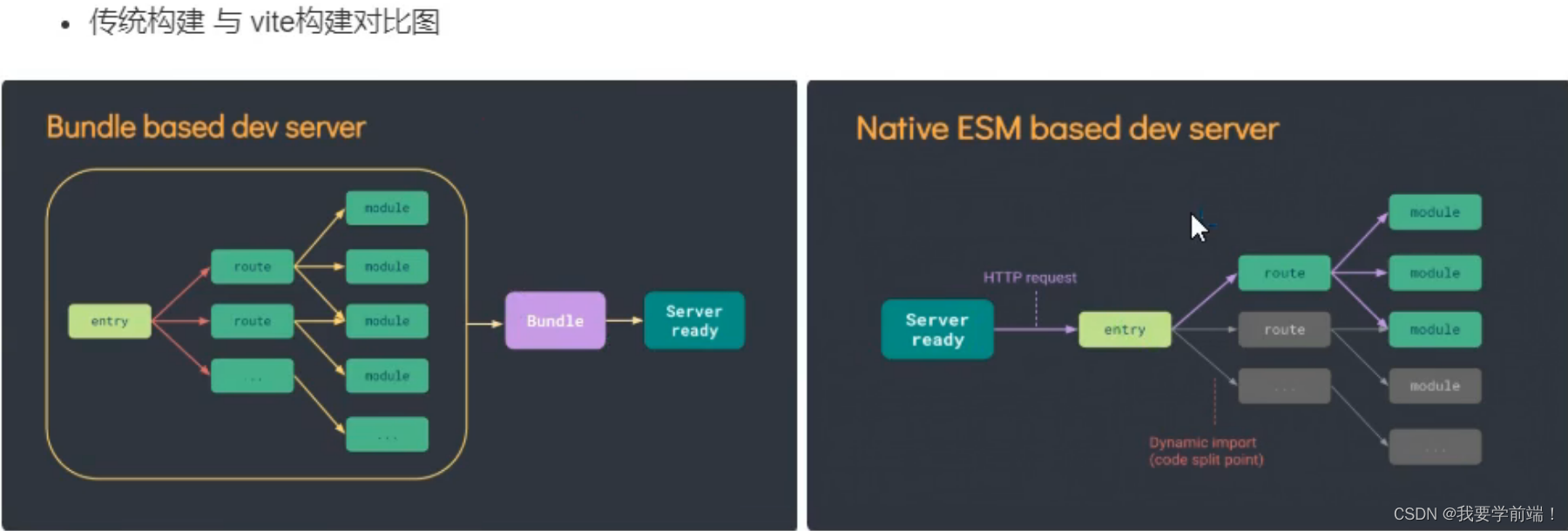
Vue3_02 创建Vue3.0工程
1.使用 vue-cli 创建 ## 查看 vue/cli 版本,确保 vue/cli 版本在4.5.0以上 vue -V 或 vue --version## 安装或升级你的 vue/cli npm install -g vue/cli## 创建 vue create vue_test## 启动 cd vue-test npm run serve 2.使用 vite 创建 什么是vite?——新一代…...

Arduino ESP 8266 ESPAsyncWebServer AsyncCallbackJsonWebHandler
Arduino-ESP 8266 踩坑(一) ESPAsyncWebServer AsyncCallbackJsonWebHandler 在使用 ESPAsyncWebServer 时 由于我想用 asyncWebServer 通过 application/json POST 请求拿数据, 就翻看了 ESPAsyncWebServer 的 git 文档, 他是这样说的 : //JSON body handling with ArduinoJ…...
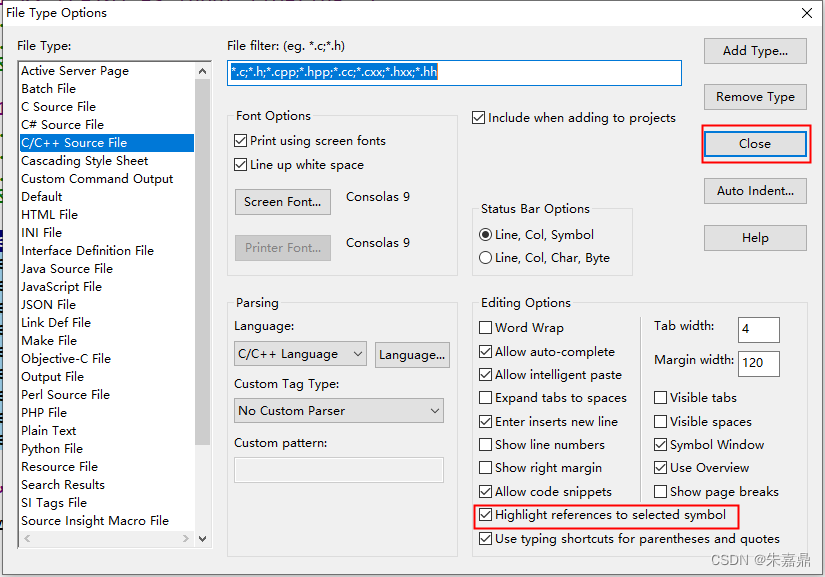
Source Insight_突出显示对选定字符的引用
1、突出显示对选定字符的引用 在Source Insight中,当我们选中一个函数或者变量的时候,关于它的所有引用地方都高亮显示,想要实现效果如下。 2、配置方法 (1)点击"Options"→“File Type options...” (2)勾选“Highlight referenc…...

高等数学上册 第五章 定积分 知识点总结
定积分 定积分的性质: ( 1 ) ∫ a b [ α f ( x ) β g ( x ) ] d x α ∫ a b f ( x ) d x β ∫ a b g ( x ) d x ( 2 )设 a < c < b ,则 ∫ a b f ( x ) d x ∫ a c f ( x ) d x ∫ c b f ( …...

【无标题】uniapp引入萤石云 真机无法运行 踩坑集合
Uniapp 接入萤石云 踩坑 1.先用了 UIKit Javascript 就是在 pc端 那套流程 npm install ezuikit-jsimport EZUIKit from ezuikit-js;这套流程貌似只适用于pc端,我在接入uniapp的时候没看官网 以为都是一套流程,然后就在uniapp中也来了这一套࿰…...

python函数
目录 函数基本语法 函数定义 函数调用 形式参数和实际参数 None类型 None主要作用 函数的说明文档 语法 变量的作用域 变量分类 global关键字 不加global关键字 加global关键字 函数的多返回值 多返回值写法 函数的四种传参方式 位置参数 关键字参数 缺省参…...

【Linux】进程间通信——system V共享内存
目录 写在前面的话 System V共享内存原理 System V共享内存的建立 代码实现System V共享内存 创建共享内存shmget() ftok() 删除共享内存shmctl() 挂接共享内存shmat() 取消挂接共享内存shmdt() 整体通信流程的实现 写在前面的话 上一章我们讲了进程间通信的第一种方式…...
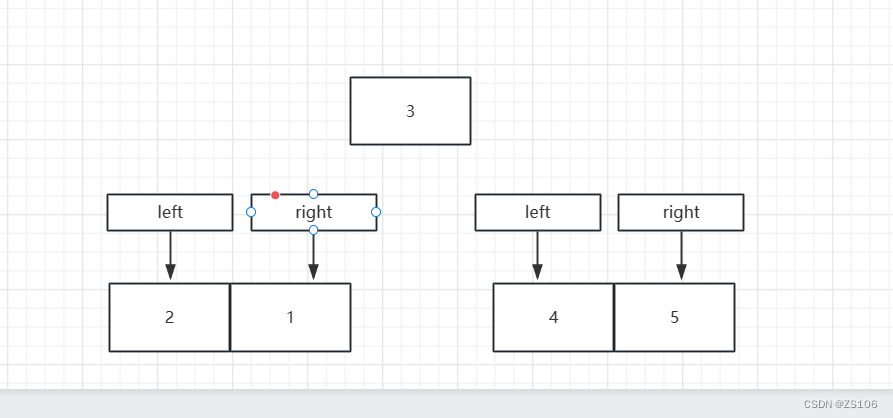
【数据结构】快速排序
快速排序是一种高效的排序算法,其基本思想是分治法。它将一个大问题分解成若干个小问题进行解决,最后将这些解合并得到最终结果。 快速排序的主要思路如下: 选择一个基准元素:从待排序的数组中选择一个元素作为基准(…...

人机融合智能中的事实与价值
在人机融合智能中,事实和价值分别扮演着不同的角色和功能。 事实是客观存在的真实描述,可以通过数据、观测和验证等方式获取。在人机融合智能中,人工智能通过处理和分析大量的数据来提供客观事实的支持。例如,在搜索引擎中&#x…...

JVM | 从类加载到JVM内存结构
引言 我在上篇文章:JVM | 基于类加载的一次完全实践 中为你讲解如何请“建筑工人”来做一些定制化的工作。但是,大型的Java应用程序时,材料(类)何止数万,我们直接堆放在工地上(JVM)…...
Golang之路---04 并发编程——WaitGroup
WaitGroup 为了保证 main goroutine 在所有的 goroutine 都执行完毕后再退出,前面使用了 time.Sleep 这种简单的方式。 由于写的 demo 都是比较简单的, sleep 个 1 秒,我们主观上认为是够用的。 但在实际开发中,开发人员是无法…...

React(4)
1.属性(props)初始 状态state都是组件内部写的,也就是A组件内的state就只能A组件里面用,其他组件复用不了。因此属性props就可以。 比如一个导航栏,首页有,购物车有,我的有,他们三个…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
