高等数学上册 第五章 定积分 知识点总结
定积分
定积分的性质: ( 1 ) ∫ a b [ α f ( x ) + β g ( x ) ] d x = α ∫ a b f ( x ) d x + β ∫ a b g ( x ) d x ( 2 )设 a < c < b ,则 ∫ a b f ( x ) d x = ∫ a c f ( x ) d x + ∫ c b f ( x ) d x ( 3 )在 [ a , b ] 上 f ( x ) ≡ 1 ,则 ∫ a b f ( x ) d x = b − a ( 4 )在 [ a , b ] 上 f ( x ) ≥ 0 ,则 ∫ a b f ( x ) d x ≥ 0 ( 5 )设 m 和 M 分别在 f ( x ) 在 [ a , b ] 上的最小值和最大值, 则 m ( b − a ) ≤ ∫ a b f ( x ) d x ≤ M ( b − a ) ( 6 )定积分中值定理: ∫ a b f ( x ) d x = f ( ξ ) ( b − a ) ( a ≤ ξ ≤ b ) 积分上限的函数及其导数: 积分上限的函数 Φ ( x ) = ∫ a x f ( t ) d t 其导数为 f ( x ) 牛顿 − 莱布尼茨公式(微积分基本公式): ∫ a b f ( x ) d x = F ( b ) − F ( a ) 如下等式所示,牛顿莱布尼茨公式沟通了微分学与积分学之间的联系 ∫ a b f ( x ) d x = f ( ξ ) ( b − a ) ⏟ 定积分中值定理 = F ′ ( ξ ) ( b − a ) = F ( b ) − F ( a ) ⏟ 微分中值定理 ⏟ 牛顿 − 莱布尼茨公式 定积分的性质:\\ (1)\int_a^b[\alpha f(x)+\beta g(x)]dx=\alpha\int_a^bf(x)dx+\beta\int_a^bg(x)dx \\ (2)设a<c<b,则\int_a^bf(x)dx=\int_a^cf(x)dx+\int_c^bf(x)dx \\ (3)在[a,b]上f(x)\equiv1,则\int_a^bf(x)dx=b-a \\ (4)在[a,b]上f(x)\ge0,则\int_a^bf(x)dx\ge0 \\ (5)设m和M分别在f(x)在[a,b]上的最小值和最大值,\\ 则m(b-a)\le\int_a^bf(x)dx\le M(b-a) \\ (6)定积分中值定理:\int_a^bf(x)dx=f(\xi)(b-a)(a\le\xi\le b)\\ \,\\\,\\ 积分上限的函数及其导数: \\ 积分上限的函数\Phi(x)=\int_a^xf(t)dt其导数为f(x) \\ \,\\\,\\ 牛顿-莱布尼茨公式(微积分基本公式):\\ \int_a^bf(x)dx=F(b)-F(a) \\ 如下等式所示,牛顿莱布尼茨公式沟通了微分学与积分学之间的联系 \\ \begin{matrix}\underbrace{\begin{matrix}\underbrace{\int_a^bf(x)dx=f(\xi)(b-a)} \\ 定积分中值定理\end{matrix} =\begin{matrix}\underbrace{F'(\xi)(b-a)=F(b)-F(a)} \\ 微分中值定理\end{matrix} } \\ 牛顿-莱布尼茨公式\end{matrix} 定积分的性质:(1)∫ab[αf(x)+βg(x)]dx=α∫abf(x)dx+β∫abg(x)dx(2)设a<c<b,则∫abf(x)dx=∫acf(x)dx+∫cbf(x)dx(3)在[a,b]上f(x)≡1,则∫abf(x)dx=b−a(4)在[a,b]上f(x)≥0,则∫abf(x)dx≥0(5)设m和M分别在f(x)在[a,b]上的最小值和最大值,则m(b−a)≤∫abf(x)dx≤M(b−a)(6)定积分中值定理:∫abf(x)dx=f(ξ)(b−a)(a≤ξ≤b)积分上限的函数及其导数:积分上限的函数Φ(x)=∫axf(t)dt其导数为f(x)牛顿−莱布尼茨公式(微积分基本公式):∫abf(x)dx=F(b)−F(a)如下等式所示,牛顿莱布尼茨公式沟通了微分学与积分学之间的联系 ∫abf(x)dx=f(ξ)(b−a)定积分中值定理= F′(ξ)(b−a)=F(b)−F(a)微分中值定理牛顿−莱布尼茨公式
例题
( 1 )计算导数: d d x ∫ sin x cos x cos ( π t 2 ) d t 原式 = d d x [ ∫ 0 cos x cos ( π t 2 ) d t − ∫ 0 sin x cos ( π t 2 ) d t ] = − sin x cos ( π cos 2 x ) − cos x cos ( π sin 2 x ) ( 2 )求由参数表达式 x = ∫ 0 t sin u d u , y = ∫ 0 t cos u d u 所确定的函数对 x 的导数 d y d x d y d x = d y d t / d x d t = cos t sin t = cot t ( 3 ) d d x ∫ 0 x 2 1 + t 2 d t = 2 x 1 + x 4 ( 4 )证明 f ( x ) = ∫ 1 x 1 + t 3 d t 在 [ − 1 , + ∞ ) 上单调增,并求 ( f − 1 ) ′ ( 0 ) 首先,显然 f ( x ) 在 [ − 1 , + ∞ ) ,且 f ′ ( x ) = 1 + x 3 ≥ 0 ,因此单调增 那如何求其反函数在 0 这点上的导数呢,首先求原函数即 1 + x 3 的不定积分不好求 但我们可以从目标出发,如下: ( f − 1 ) ′ ( 0 ) = 1 f ′ ( x 0 ) ,这里的 x 0 满足 f ( x 0 ) = 0 如果要让积分为 0 ,令积分上限 = 积分下限即可,求得 x 0 = 1 f ′ ( 1 ) 好求啊,即 1 + 1 3 = 2 ,因此最终结果为 1 2 (1)计算导数:\frac{d}{dx}\int_{\sin x}^{\cos x}\cos(\pi t^2)dt \\ 原式=\frac{d}{dx}[\int_{0}^{\cos x}\cos(\pi t^2)dt-\int_{0}^{\sin x}\cos(\pi t^2)dt] \\ =-\sin x\cos(\pi \cos ^2x)-\cos x\cos(\pi \sin ^2x) \\ \,\\ (2)求由参数表达式x=\int_0^t\sin udu,y=\int_0^t\cos udu所确定的函数对x的导数\frac{dy}{dx} \\ \frac{dy}{dx}=\frac{dy}{dt}/\frac{dx}{dt}=\frac{\cos t}{\sin t}=\cot t \\ \,\\ (3)\frac{d}{dx}\int_{0}^{x^2}\sqrt{1+t^2}dt=2x\sqrt{1+x^4} \\ \,\\ (4)证明f(x)=\int_1^x\sqrt{1+t^3}dt在[-1,+\infty)上单调增,并求(f^{-1})'(0) \\ 首先,显然f(x)在[-1,+\infty),且f'(x)=\sqrt{1+x^3}\ge0,因此单调增 \\ 那如何求其反函数在0这点上的导数呢,首先求原函数即\sqrt{1+x^3}的不定积分不好求 \\ 但我们可以从目标出发,如下: \\ (f^{-1})'(0)=\frac{1}{f'(x_0)},这里的x_0满足f(x_0)=0 \\ 如果要让积分为0,令积分上限=积分下限即可,求得x_0=1 \\ f'(1)好求啊,即\sqrt{1+1^3}=\sqrt{2},因此最终结果为\frac{1}{\sqrt2} (1)计算导数:dxd∫sinxcosxcos(πt2)dt原式=dxd[∫0cosxcos(πt2)dt−∫0sinxcos(πt2)dt]=−sinxcos(πcos2x)−cosxcos(πsin2x)(2)求由参数表达式x=∫0tsinudu,y=∫0tcosudu所确定的函数对x的导数dxdydxdy=dtdy/dtdx=sintcost=cott(3)dxd∫0x21+t2dt=2x1+x4(4)证明f(x)=∫1x1+t3dt在[−1,+∞)上单调增,并求(f−1)′(0)首先,显然f(x)在[−1,+∞),且f′(x)=1+x3≥0,因此单调增那如何求其反函数在0这点上的导数呢,首先求原函数即1+x3的不定积分不好求但我们可以从目标出发,如下:(f−1)′(0)=f′(x0)1,这里的x0满足f(x0)=0如果要让积分为0,令积分上限=积分下限即可,求得x0=1f′(1)好求啊,即1+13=2,因此最终结果为21
相关文章:

高等数学上册 第五章 定积分 知识点总结
定积分 定积分的性质: ( 1 ) ∫ a b [ α f ( x ) β g ( x ) ] d x α ∫ a b f ( x ) d x β ∫ a b g ( x ) d x ( 2 )设 a < c < b ,则 ∫ a b f ( x ) d x ∫ a c f ( x ) d x ∫ c b f ( …...

【无标题】uniapp引入萤石云 真机无法运行 踩坑集合
Uniapp 接入萤石云 踩坑 1.先用了 UIKit Javascript 就是在 pc端 那套流程 npm install ezuikit-jsimport EZUIKit from ezuikit-js;这套流程貌似只适用于pc端,我在接入uniapp的时候没看官网 以为都是一套流程,然后就在uniapp中也来了这一套࿰…...

python函数
目录 函数基本语法 函数定义 函数调用 形式参数和实际参数 None类型 None主要作用 函数的说明文档 语法 变量的作用域 变量分类 global关键字 不加global关键字 加global关键字 函数的多返回值 多返回值写法 函数的四种传参方式 位置参数 关键字参数 缺省参…...

【Linux】进程间通信——system V共享内存
目录 写在前面的话 System V共享内存原理 System V共享内存的建立 代码实现System V共享内存 创建共享内存shmget() ftok() 删除共享内存shmctl() 挂接共享内存shmat() 取消挂接共享内存shmdt() 整体通信流程的实现 写在前面的话 上一章我们讲了进程间通信的第一种方式…...
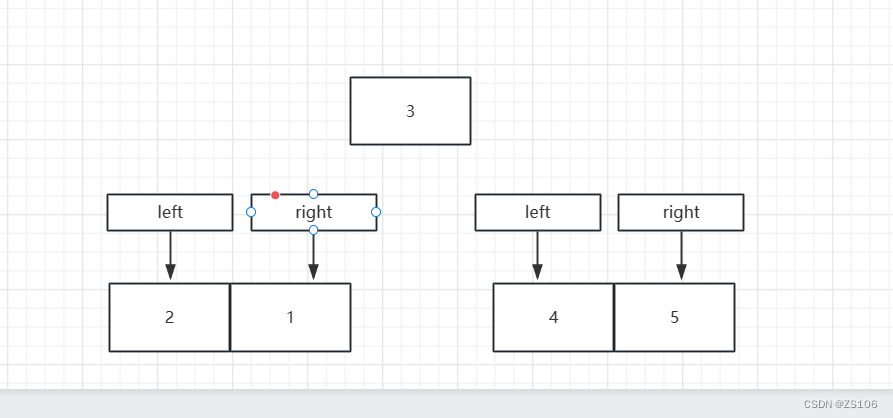
【数据结构】快速排序
快速排序是一种高效的排序算法,其基本思想是分治法。它将一个大问题分解成若干个小问题进行解决,最后将这些解合并得到最终结果。 快速排序的主要思路如下: 选择一个基准元素:从待排序的数组中选择一个元素作为基准(…...

人机融合智能中的事实与价值
在人机融合智能中,事实和价值分别扮演着不同的角色和功能。 事实是客观存在的真实描述,可以通过数据、观测和验证等方式获取。在人机融合智能中,人工智能通过处理和分析大量的数据来提供客观事实的支持。例如,在搜索引擎中&#x…...

JVM | 从类加载到JVM内存结构
引言 我在上篇文章:JVM | 基于类加载的一次完全实践 中为你讲解如何请“建筑工人”来做一些定制化的工作。但是,大型的Java应用程序时,材料(类)何止数万,我们直接堆放在工地上(JVM)…...
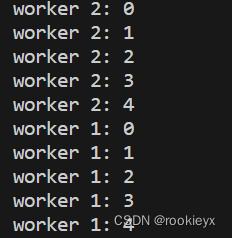
Golang之路---04 并发编程——WaitGroup
WaitGroup 为了保证 main goroutine 在所有的 goroutine 都执行完毕后再退出,前面使用了 time.Sleep 这种简单的方式。 由于写的 demo 都是比较简单的, sleep 个 1 秒,我们主观上认为是够用的。 但在实际开发中,开发人员是无法…...

React(4)
1.属性(props)初始 状态state都是组件内部写的,也就是A组件内的state就只能A组件里面用,其他组件复用不了。因此属性props就可以。 比如一个导航栏,首页有,购物车有,我的有,他们三个…...
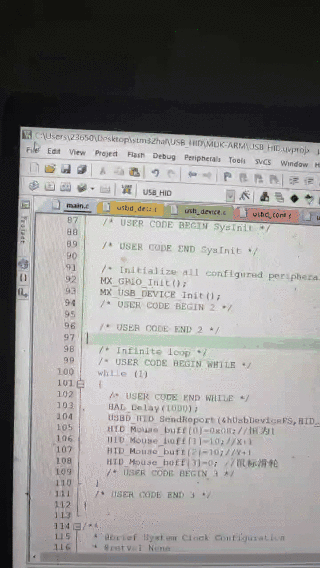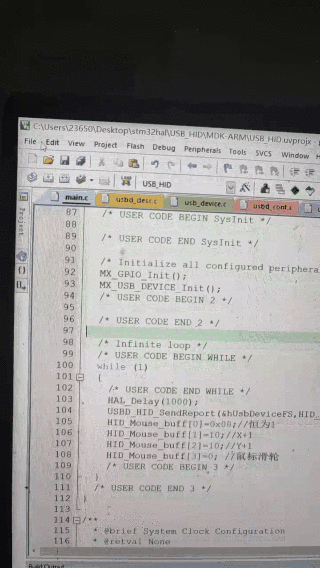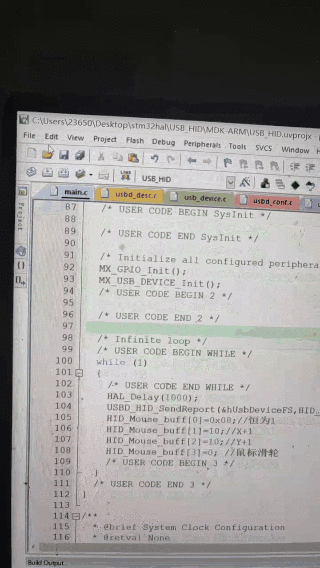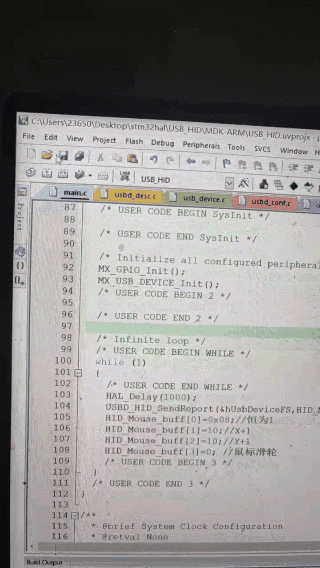
STM32 CubeMX USB_(HID 鼠标和键盘)
STM32 CubeMX STM32 CubeMX USB_HID(HID 鼠标和键盘) STM32 CubeMX前言 《鼠标小节》一、STM32 CubeMX 设置USB时钟设置USB使能UBS功能选择 二、代码部分添加代码鼠标发送给PC的数据解析实验效果 《键盘小节》STM32 CubeMX 设置(同上…...
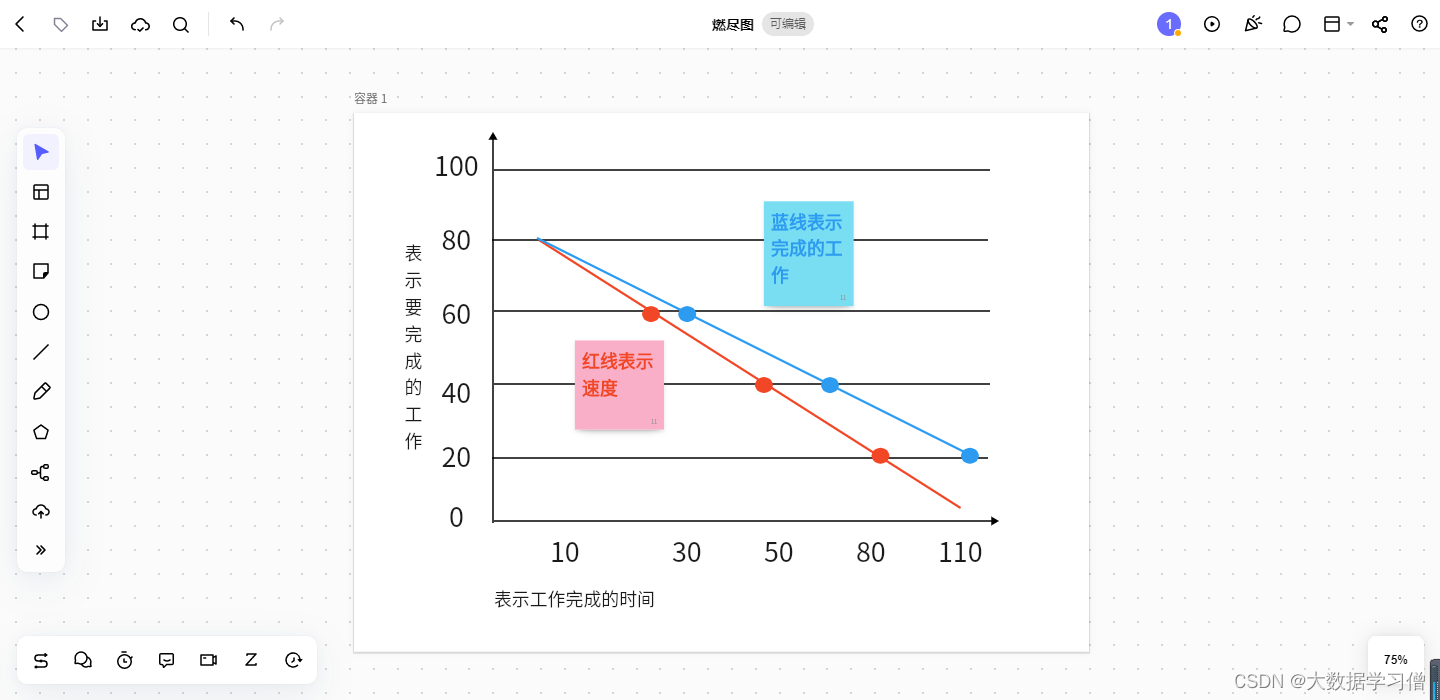
[PM]敏捷开发之Scrum总结
在项目管理中,不少企业和项目团队也发现传统的项目管理模式已不能很好地适应今天的项目环境的要求。因此,敏捷项目管理应运而生,本文将为大家介绍Scrum敏捷项目管理以及应用方法。 什么是Scrum敏捷项目管理 敏捷项目管理作为新兴的项目管理模…...

大数据Flink(五十七):Yarn集群环境(生产推荐)
文章目录 Yarn集群环境(生产推荐) 一、准备工作...
web集群学习:源码安装nginx配置启动服务脚本
1、源码安装nginx,并提供服务脚本。 1、源码安装会有一些软件依赖 (1)检查并安装 Nginx 基础依赖包 pcre-devel 、openssl-devel # rpm -qa | egrep pcre-devel | openssl-devel(2)安装 Nginx 所需的 pcre 库 正则支…...

LNMP
lNmp安装: 一、LNMP LNMP架构是目前成熟的企业网站应用模式之一,指的是协同工作的一整套系统和相关软件, 能够提供动态Web站点服务及其应用开发环境。LNMP是一个缩写词,具体包括Linux操作系统、nginx网站服务器、MySQL数据库服务…...

Python网络爬虫在信息采集中的应用及教程
Python网络爬虫在信息采集中的应用与法律警告 摘要 随着互联网的发展,我们每天都面临着海量的信息。这些信息蕴含着无尽的价值,而要从中获取有用的数据,网络爬虫就成了我们的得力助手。Python作为一门简单而又强大的编程语言,被…...

云主机测试Flink磁盘满问题解决
问题描述: 使用云主机测试Flink时,根目录满了。 经排查发现运行Flink任务后根目录空间一直在减少,最后定位持续增加的目录是/tmp目录 解决方法: 修改Flink配置使用一个相对较大的磁盘目录做为Flink运行时目录 # Override the…...

iOS开发-NSOperationQueue实现上传图片队列
iOS开发-NSOperationQueue实现上传图片队列 在开发中,遇到发帖需要上传图片,需要上传队列,这时候用到了NSOperationQueue 一、NSOperation与NSOperationQueue 什么NSOperation NSOperation为控制任务状态、优先级、依赖关系以及任务管理提…...

通过 CCIP 构建跨链应用(5 个案例)
Chainlink 的跨链互操作性协议(CCIP)是一种新的通用跨链通信协议,为智能合约开发人员提供了以最小化信任的方式在区块链网络之间传输数据和通证的能力。 目前,部署在多个区块链上的应用程序面临着资产、流动性和用户的碎片化问题…...

基于 yolov8 的人体姿态评估
写在前面 工作中遇到,简单整理博文内容为使用预训练模型的一个预测 Demo测试图片来源与网络,如有侵权请告知理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停…...

计算机视觉(六)图像分类
文章目录 常见的CNNAlexnet1乘1的卷积 VGG网络Googlenet(Inception V1、V2、V3)全局平均池化总结 Resnet、ResnextResNet残差网络ResNeXt网络 应用案例VGGResnet 常见的CNN Alexnet DNN深度学习革命的开始 沿着窗口进行归一化。 1乘1的卷积 VGG网络…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
