【C语言每日一题】——猜名次
【C语言每日一题】——猜名次😎
- 前言🙌
- 猜名次🙌
- 解题思路分享:😍
- 解题源码分享:😍
- 总结撒花💞

😎博客昵称:博客小梦
😊最喜欢的座右铭:全神贯注的上吧!!!
😊作者简介:一名热爱C/C++,算法等技术、喜爱运动、热爱K歌、敢于追梦的小博主!
😘博主小留言:哈喽!😄各位CSDN的uu们,我是你的博客好友小梦,希望我的文章可以给您带来一定的帮助,话不多说,文章推上!欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
前言🙌
哈喽各位友友们😊,我今天又学到了很多有趣的知识,现在迫不及待的想和大家分享一下!😘我仅已此文,和大家分享【C语言每日一题】——猜名次~ 将现实中的生活问题转化为代码讲述,非常有意思的一到题目~ 都是精华内容,可不要错过哟!!!😍😍😍
猜名次🙌
猜名次
题目描述:5位运动员参加了10米台跳水比赛,有人让他们预测比赛结果:
A选手说:B第二,我第三;
B选手说:我第二,E第四;
C选手说:我第一,D第二;
D选手说:C最后,我第三;
E选手说:我第四,A第一;
比赛结束后,每位选手都说对了一半,请编程确定比赛的名次。
解题思路分享:😍
- 这是一道和十分有意思的题目。考虑到一共五个人,直接模拟推理有些太难,可以利用遍历所有可能性来解决。
- 将每个人从第1到第5来一遍,则一共会产生5^5种可能性,这个只需要一个5层循环即可搞定。
- 多看几遍五个人描述的话语和题目所给的提示。并用代码写出相应的 if ()中的判断语句 。
- 但是这样会导致一些不期望出现的结果出现,但是会出现两个人或者更多的人名次相同的情况,例如两个第1,三个第2这样的,所以即使满足了条件,也要查看一下五个人的名次是否重复。 所以在if的判断条件中将这些进行一个把控,将重复的情况进行一个筛选控制即可。
解题源码分享:😍
#include<stdio.h>int main(){int a = 0, b = 0, c = 0, d = 0, e = 0;for (int i = 1; i < 5; i++){a = i;for (int j = 1; j <= 5; j++){b = j;for (int k = 1; k <= 5; k++){c = k;for (int l = 1; l <= 5; l++){d = l;for (int m = 1; m <= 5; m++){e = m;if ((b == 2 || a == 3) &&( b == 2 || e == 4) && (c == 1 || d == 2 )&&(c == 5 || d == 3 )&&( e == 4 || a == 1) && (a != b) && (a != c)&& (a != d) && (a != e )&&( b != c) &&( b != d ) && (b != e) && (c!= d)&& (c != e )&& (d != e)){printf("a = %d,b = %d,c = %d. d = %d,e = %d\n",a,b,c,d,e);}}}}}}return 0;}程序输出结果验证: 😊
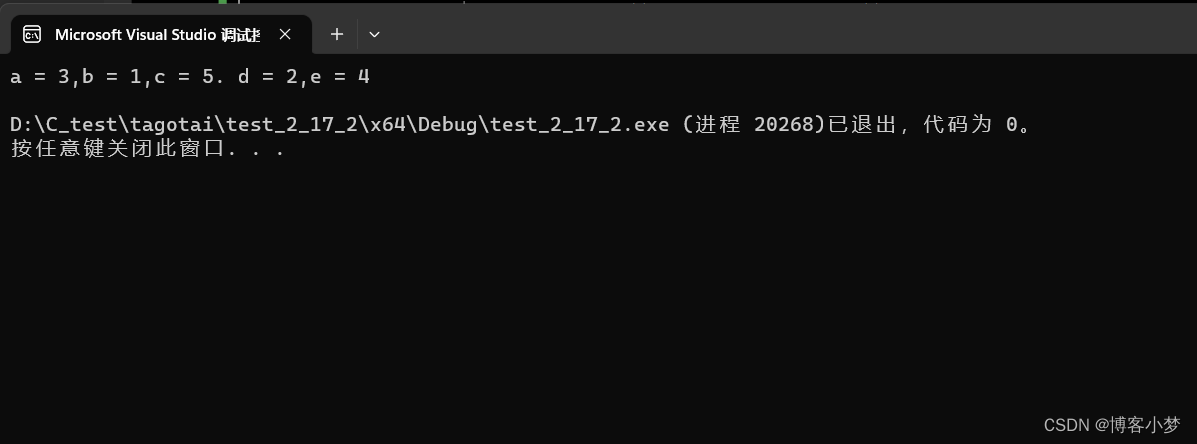 然后我通过程序运行的结果和题目内容对比后,是符合题目要求的答案。 😍
然后我通过程序运行的结果和题目内容对比后,是符合题目要求的答案。 😍
总结撒花💞
本篇文章旨在分享C语言详解【C语言每日一题】——猜名次。希望大家通过阅读此文有所收获!但是我觉得我实现的这个算法的效率有点低,要用到五层循环,各位聪明的uu们有没有更高效的解题算法呢?有的话可以私信笨笨的小梦😊,教教俺!!!😘如果我写的有什么不好之处,请在文章下方给出你宝贵的意见😊。如果觉得我写的好的话请点个赞赞和关注哦~😘😘😘
相关文章:

【C语言每日一题】——猜名次
【C语言每日一题】——猜名次😎前言🙌猜名次🙌解题思路分享:😍解题源码分享:😍总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右铭:全神…...

Agilent E4982A、Keysight E4982A、LCR 表,1 MHz 至 3 GHz
Agilent E4982A、Keysight E4982A、HP E4982A LCR 表,1 MHz 至 3 GHz 产品概览 KEYSIGHT E4982A(安捷伦) Keysight E4982A LCR 表为需要高频(1 MHz 至 3 GHz)阻抗测试的无源元件制造行业提供一流的性能,…...

SAP 系统的配置传输
在SAP项目的实施过程中,经常会遇到关于配置传输的问题。即我们在某个client下面做系统配置,配好了之后再传到其他系统之中。 配置传输分为两种情况:同服务器配置传输,异服务器配置传输。同服务器配置传输: 在DEV配置cl…...
)
华为OD机试 - 喊七(Python)
喊七 题目 喊 7,是一个传统的聚会游戏, N 个人围成一圈,按顺时针从1 - 7编号, 编号为1的人从1开始喊数, 下一个人喊得数字是上一个人喊得数字+1, 但是当将要喊出数字7的倍数或者含有7的话, 不能喊出,而是要喊过。 假定N个人都没有失误。 当喊道数字k时, 可以统计每…...
Docker下快速搭建RabbitMQ单例及集群
引子生命在于折腾,为上数据实时化用到了消息传送的内容,当时也和总公司人员商量选型,kafka不能区分分公司就暂定用了RbtMQ刚好个人也在研究容器及分布式部署相关内容就在docker上实践单机 docker(要想快 先看问题 避免踩坑&#x…...

python代码写开心消消乐
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放,树高千尺,落叶归根人生不易,人间真情 目录 一.python是什么 二.游戏代码效果呈现 三.主代...
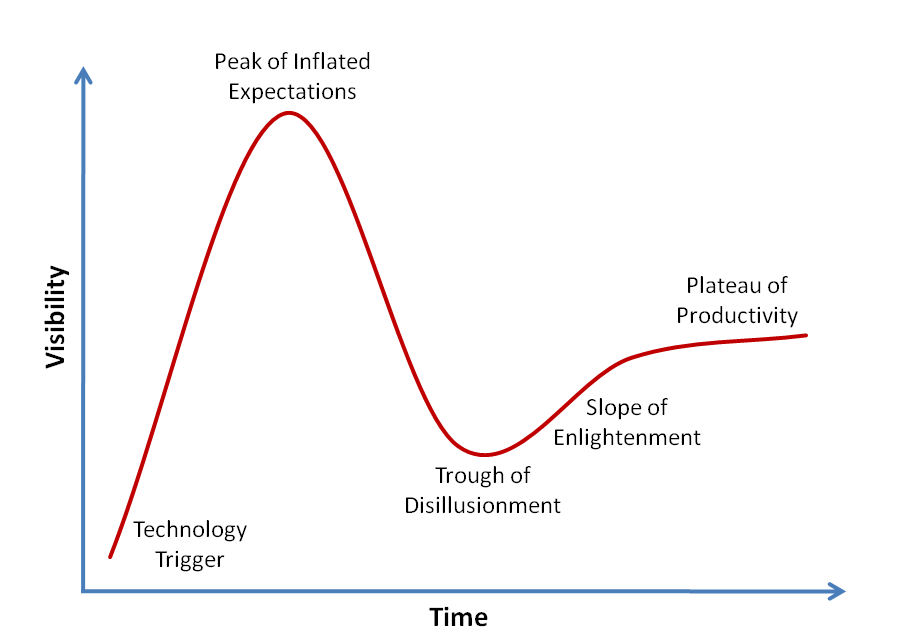
【郭东白架构课 模块一:生存法则】09|法则四:为什么要顺应技术的生命周期?
你好,我是郭东白。今天我们来讲架构师的第四条生存法则,那就是尊重技术的生命周期。 人类的各种活动都要遵循事物的客观生命周期。不论是农业社会种田打渔,还是资本社会投资创业,行动太早或太晚,都会颗粒无收。技术也…...
Linux之进程控制
一.进程创建 1.1 fork函数 我们创建进程的方式有./xxx和fork()两种 在linux中fork函数时非常重要的函数,它从已存在进程中创建一个新进程。新进程为子进程,而原进程为父进程。 #include <unistd.h> pid_t fork(void); 返回值:自进程…...

SpringBoot社区版专业版带你配置热部署
💟💟前言 友友们大家好,我是你们的小王同学😗😗 今天给大家打来的是 SpringBoot社区版专业版带你配置热部署 希望能给大家带来有用的知识 觉得小王写的不错的话麻烦动动小手 点赞👍 收藏⭐ 评论…...

影响AFE采样精度的因素有哪些?
**AFE(Analog Front End)**是模拟前端电路的缩写,它是模拟信号传感器和数字信号处理器之间的连接点。AFE采样精度是指模拟信号被数字化后的准确度,对于很多电子设备来说,这是一个至关重要的性能指标。本文将介绍影响AF…...

mysqlbackup备份报error:redo log was overwritten
问题原因 备份时redo log被覆盖 解决方案 方法1:增加innodb_log_file_size、innodb_log_files_in_group大小,需要重启数据库 vi my.cnf innodb_log_file_size 2G innodb_log_files_in_group 4 方法2: 动态配置redo log archive,不需要重启…...

Android支持库
# 支持库 注意:Android 9.0(API 级别 28)发布后,新版支持库 AndroidX 也随之诞生,它属于 Jetpack。除了现有的支持库,AndroidX 库还包含最新的 Jetpack 组件。 您可以继续使用此支持库以往的工件(这里指的是版本 27 及更早版本,且已打包为 android.support.*)在 Googl…...
Vue:filters过滤器
日期、时间格式化是Vue前端项目中较为常遇到的一个需求点,此处,围绕Vue的过滤器来介绍如何更为优雅的解决此类需求。 过滤器filters使用注意点 Vue允许开发者自定义过滤器,可以实现一些常见的文本格式化等需求。 使用时要注意的点在于&#…...
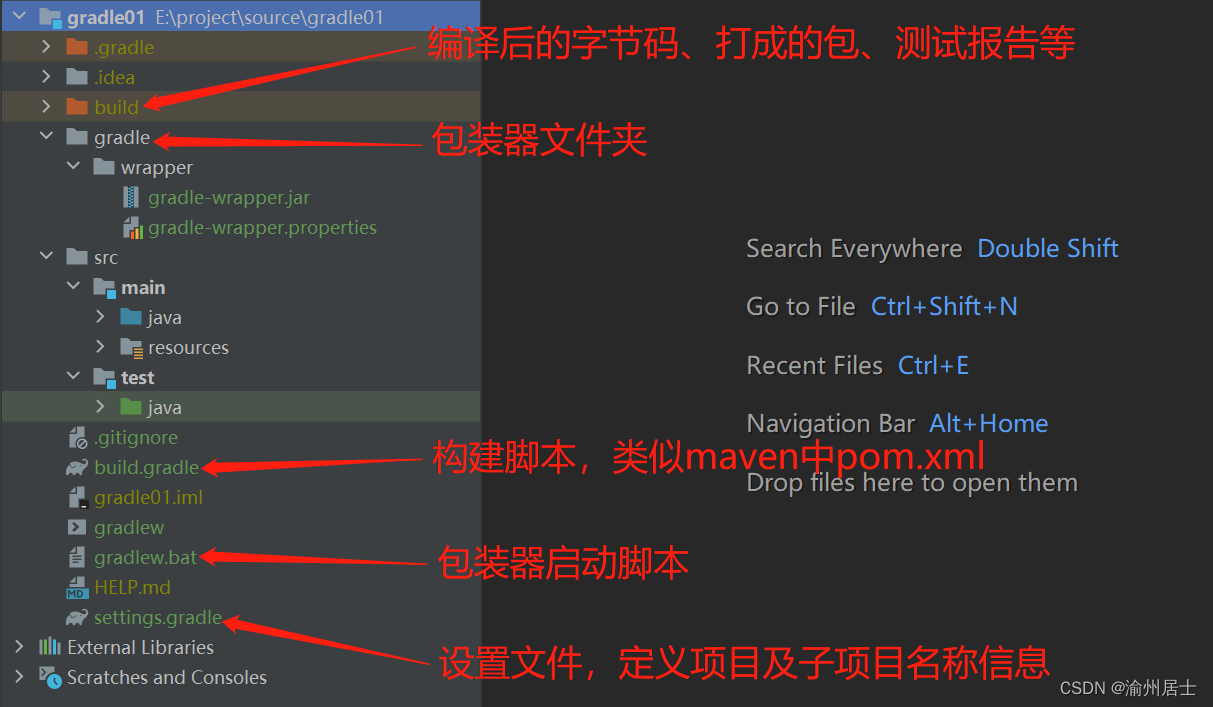
Windows环境下安装和配置Gradle
1. 概述 Gradle是Google公司基于JVM开发的一款项目构建工具,支持Maven,JCenter多种第三方仓库,支持传递性依赖管理,使用更加简洁和支持多种语言的build脚步文件,更多详情可以参阅Gradle官网 2. 下载 由于Gradle与S…...

数据结构时间空间复杂度笔记
🕺作者: 迷茫的启明星 本篇内容:数据结构时间空间复杂度笔记 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇家人们,码字不易,你的👍点赞🙌收藏❤…...
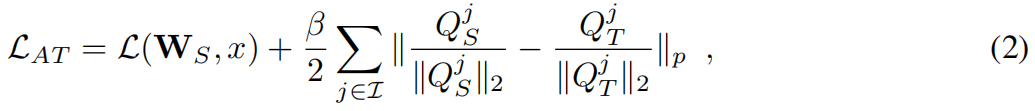
基于注意力的知识蒸馏Attention Transfer原理与代码解析
paper:Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfercode:https://github.com/megvii-research/mdistiller/blob/master/mdistiller/distillers/AT.py背景一个流行的假设是存…...

利尔达在北交所上市:总市值突破29亿元,叶文光为董事长
2月17日,利尔达科技集团股份有限公司(下称“利尔达”,BJ:832149)在北京证券交易所上市。本次上市,利尔达的发行价格为5.00元/股,发行数量为1980万股,发行市盈率为12.29倍,募资总额为…...
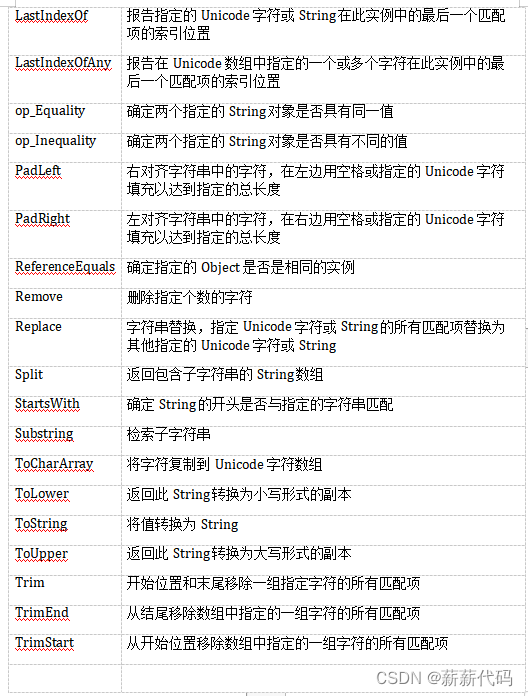
C#操作字符串方法 [万余字总结 · 详细]
C#操作字符串方法总结C#常用字符串函数大全C#常用字符串操作方法C#操作字符串方法总结C#常用字符串函数大全 Compare 比较字符串的内容,考虑文化背景(场所),确定某些字符是否相等 CompareOrdinal 与Compare一样,但不考虑文化背景 Format 格…...

极兔一面:10亿级ES海量搜索狂飙10倍,该怎么办?
背景说明: ES高性能全文索引,如果不会用,或者没有用过,在面试中,会非常吃亏。 所以ES的实操和底层原理,大家要好好准备。 另外,ES调优是一个非常、非常核心的面试知识点,大家要非…...
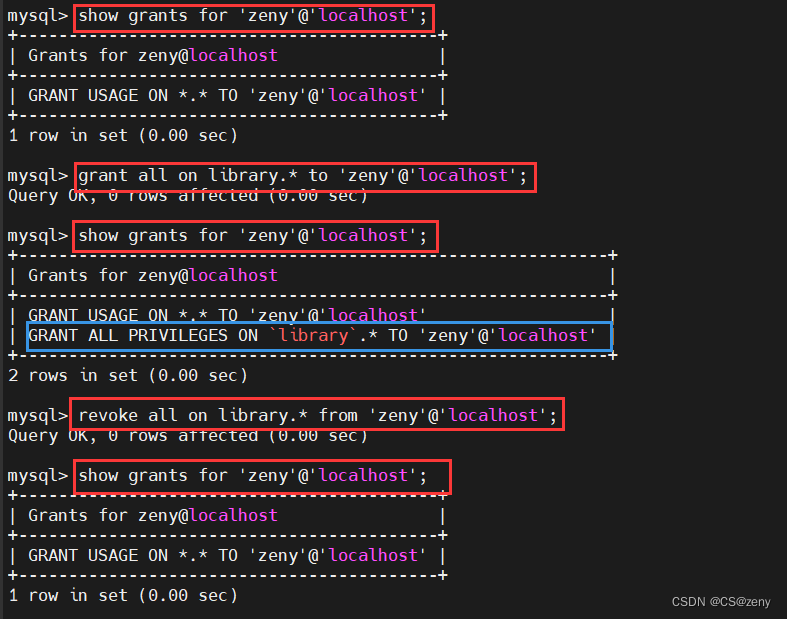
【Mysql基础 —— SQL语句(一)】
文章目录概述使用启动/停止mysql服务连接mysql客户端数据模型SQLSQL语句分类DDL数据库操作表操作查询创建数据类型修改删除DML添加数据修改数据删除数据DQL基础查询条件查询聚合函数分组查询排序查询分页查询执行顺序DCL管理用户权限控制概述 数据库(Database&#…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

