LeetCode·每日一题·1223.掷骰子模拟·记忆化搜索
作者:小迅
链接:https://leetcode.cn/problems/dice-roll-simulation/solutions/2103471/ji-yi-hua-sou-suo-zhu-shi-chao-ji-xiang-xlfcs/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
题目

示例
思路
题意 -> 给定一个字符串规定相同类型的骰子连续出现的最大值,返回投掷 n 次后能出现的 骰数 的不同序列个数
题目说是 骰子模拟,那么直接按照题目意思进行模拟呢?
想一想,掷了一个骰子(设值为 x)后,会发生什么情况?
既然题目有 rollMax 的限制,那么分类讨论:
如果和上一个骰子值相同,那么 x 的连续出现次数不能超过 rollMax[x];
如果不同,那么可以重置连续出现次数为 1。
关键词提取:「上一个骰子值」 和 「连续出现次数」
那么在回溯中就需要知道(为了方便后面转成递推,定义成剩余):
剩余掷骰子的次数,用 i 表示;
上一个骰子值,用 last 表示;
last 的剩余连续出现次数,用 left 表示。
这样就确定了递归的参数,递归的返回值就是骰子序列个数。
要递归到哪里去呢?我们可以用回溯中的经典技巧「枚举选哪个」:
如果选的骰子值和上一个相同,且 left>0,那么递归到 (i−1,last,left−1);
如果不同,设为 j,那么递归到 (i−1,j,rollMax[j]−1)。
枚举 j=0,1,2,3,4,5,把递归后的结果相加,就是当前 (i,last,left) 的答案。
递归到 n=0 时结束,返回 1,表示找到了一个合法骰子序列
整个回溯过程是有大量重复递归调用的。由于递归函数没有副作用,无论多少次调用 dfs(i,last,left) 算出来的结果都是一样的,因此可以用记忆化搜索来优化:
如果一个状态(递归入参)是第一次遇到,那么可以在返回前,把状态及其结果记到一个 cache 数组(或者哈希表)中;
如果一个状态不是第一次遇到,那么直接返回 cache 中保存的结果。
cache[n][x][y] - n 表示 当前剩余投掷次数, x 表示上一次投掷骰子值, y表示 上一次投掷骰子值 剩余的出现次数;
为啥可以到达记忆化效果,因为当前投掷结果的有效性只和上一次的投掷结果相关,「先掷 1 后掷 3」和「先掷 2 后掷 3」,都会递归到 dfs(n−2,3,rollMax[3]−1)。
如何转动态规划 :
可以去掉递归中的「递」,只保留「归」的部分,即自底向上计算。
做法:
dfs 改成 f 数组;
递归改成循环(每个参数都对应一层循环);
递归边界改成 f 数组的初始值。
代码注释超级详细
代码
const long MOD = 1e9 + 7;int dfs(int i, int last, int *rollMax, int left, int (*cache)[6][15])
{if (i == 0) return 1;int *c = (int *)&(cache[i][last][left]);if (*c >= 0) return *c;//如果之前算过就不需要重新计算long res = 0;for (int j = 0; j < 6; ++j)if (j != last) res += dfs(i - 1, j, rollMax, rollMax[j] - 1, cache);else if (left) res += dfs(i - 1, j, rollMax, left - 1, cache);return *c = res % MOD;
}int dieSimulator(int n, int* rollMax, int rollMaxSize){int cache[n][6][15];//记忆化数组memset(cache, -1, sizeof(cache)); // -1 表示没有访问过long ans = 0;for (int j = 0; j < 6; ++j)//枚举初始状态0-6ans += dfs(n - 1, j, rollMax, rollMax[j] - 1, cache);return ans % MOD;
}作者:小迅
链接:https://leetcode.cn/problems/dice-roll-simulation/solutions/2103471/ji-yi-hua-sou-suo-zhu-shi-chao-ji-xiang-xlfcs/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。class Solution {const long MOD = 1e9 + 7;
public:int dieSimulator(int n, vector<int> &rollMax) {int m = rollMax.size(), f[n][m][15];for (int j = 0; j < m; ++j)for (int k = 0; k < rollMax[j]; ++k)f[0][j][k] = 1;for (int i = 1; i < n; ++i)for (int last = 0; last < m; ++last)for (int left = 0; left < rollMax[last]; ++left) {long res = 0;for (int j = 0; j < m; ++j)if (j != last) res += f[i - 1][j][rollMax[j] - 1];else if (left) res += f[i - 1][j][left - 1];f[i][last][left] = res % MOD;}long ans = 0;for (int j = 0; j < m; ++j)ans += f[n - 1][j][rollMax[j] - 1];return ans % MOD;}
};
相关文章:

LeetCode·每日一题·1223.掷骰子模拟·记忆化搜索
作者:小迅链接:https://leetcode.cn/problems/dice-roll-simulation/solutions/2103471/ji-yi-hua-sou-suo-zhu-shi-chao-ji-xiang-xlfcs/来源:力扣(LeetCode)著作权归作者所有。商业转载请联系作者获得授权࿰…...

【GPLT 二阶题目集】L2-043 龙龙送外卖
参考地址:AcWing 4474. 龙龙送外卖(杂题选讲) 作者:yxc 感谢y总! 龙龙是“饱了呀”外卖软件的注册骑手,负责送帕特小区的外卖。帕特小区的构造非常特别,都是双向道路且没有构成环 —— 你可以…...
Maven:基础知识
Maven概念图生命周期目录工程创建测试常用命令COMPILATION ERROR : 不再支持目标选项 5。请使用 7 或更高版本。问题解决pom.xml文件properties配置示例scope配置详解概念图 依赖管理构建项目Maven 的底层核心实现项目的构建和管理必须通过插件完成,但插件本身并不包…...
Web 框架 Flask 快速入门(一)flask基础与模板
前言 课程地址:Python Web 框架 Flask 快速入门 文章目录前言🌴 Flask基础和模板🌷 一个简单的flask程序🌼 模板的使用🌴 Flask基础和模板 1、web框架的作用 避免重复造轮子,app程序不必关心于服务器的沟…...
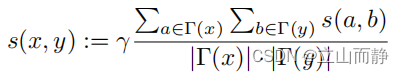
1CN/Jaccard/PA/AA/RA/Katz/PageRank/SimRank
common neighbors(CN) 公共邻居的数量。 Jaccard 用于比较有限样本集之间的相似性与差异性。Jaccard系数值越大,样本相似度越高。 preferential attachment(PA) 节点倾向于连接到节点度较高的节点上,&…...
YOLOv5-Backbone模块实现
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍦 参考文章地址: 365天深度学习训练营-第P8周:YOLOv5-Backbone模块实现🍖 作者:K同学啊一、前期准备1.设置GPUimport torch from torch impor…...
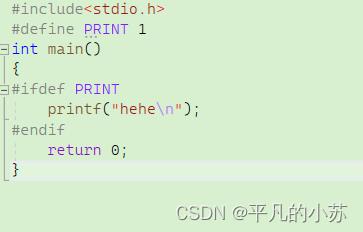
【C语言】程序环境和预处理
🌇个人主页:平凡的小苏 📚学习格言:别人可以拷贝我的模式,但不能拷贝我不断往前的激情 🛸C语言专栏:https://blog.csdn.net/vhhhbb/category_12174730.html 小苏希望大家能从这篇文章中收获到许…...
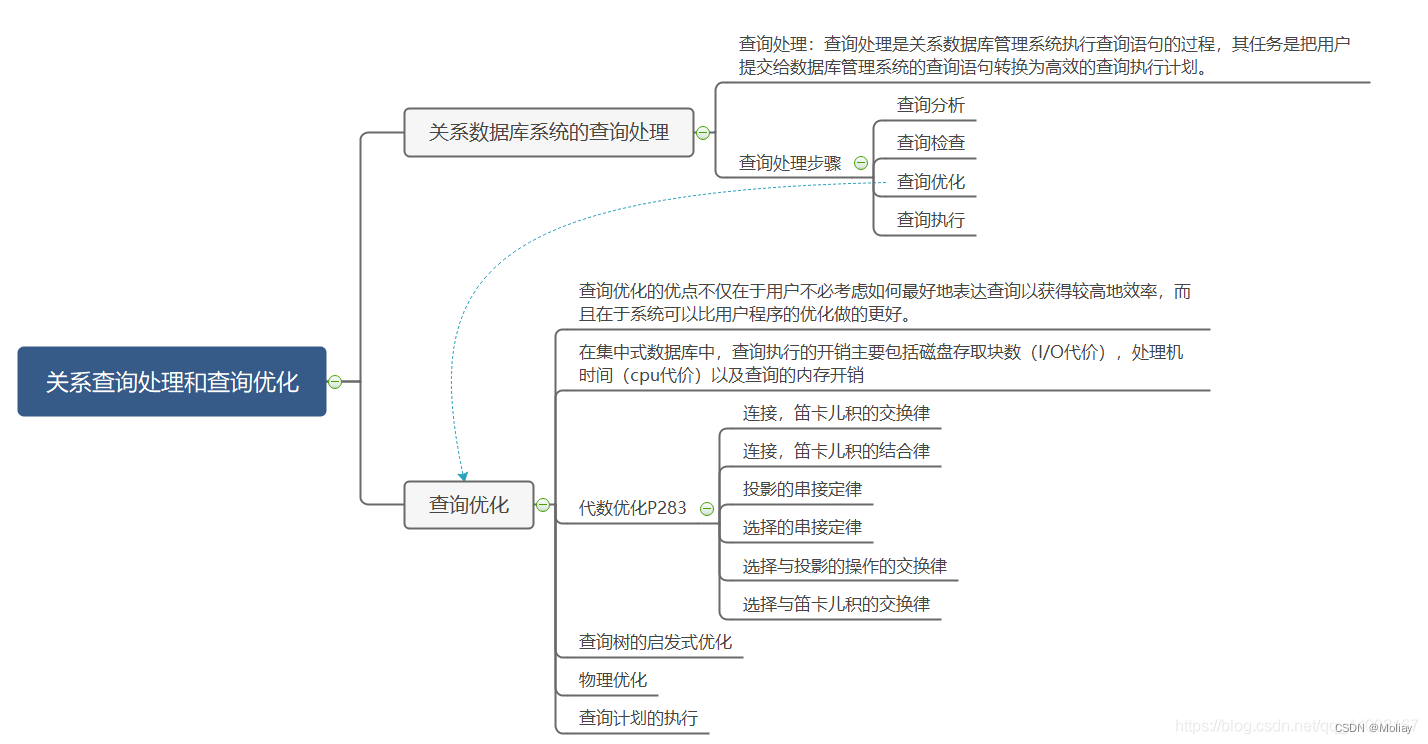
9.关系查询处理和查询优化
其他章节索引 梳理 名词解释 代数优化:是指关系代数表达式的优化,也即按照一定规则,通过对关系代数表达式进行等价变换,改变代数表达式中操作的次序和组合,使查询更高效物理优化:是指存取路径和底层操作算…...

计算机组成原理(三)
5.掌握定点数的表示和应用(主要是无符号数和有符号数的表示、机器数的定点表示、数的机器码表示); 定点数:小数点位置固定不变。 定点小数:小数点固定在数值位与符号位之间; 定点整数:小…...

C. Least Prefix Sum codeforces每日一题
🚀前言 🚀 大家好啊,这里是幸麟 🧩 一名普通的大学牲,最近在学习算法 🧩每日一题的话难度的话是根据博主水平来找的 🧩所以可能难度比较低,以后会慢慢提高难度的 🧩此题标…...
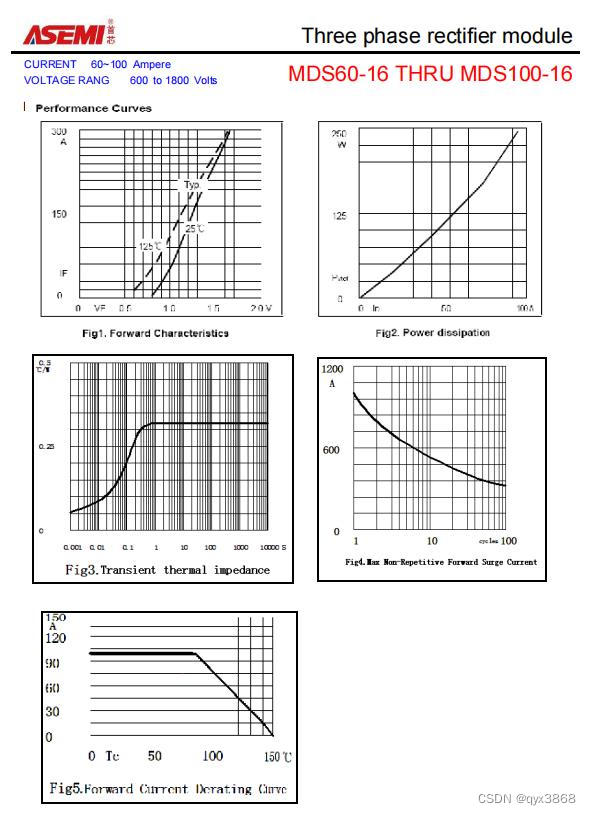
ASEMI三相整流模块MDS100-16图片,MDS100-16尺寸
编辑-Z ASEMI三相整流模块MDS100-16参数: 型号:MDS100-16 最大重复峰值反向电压(VRRM):1600V 最大RMS电桥输入电压(VRMS):1700V 最大平均正向整流输出电流(IF&#…...

【第37天】斐波那契数列与爬楼梯 | 迭代的鼻祖,递推与记忆化
本文已收录于专栏🌸《Java入门一百例》🌸学习指引序、专栏前言一、递推与记忆化二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析5.原题链接三、【例题1】1、题目描述2.解题思路3、模板代码4、代码解析5、原题链接三、推荐专栏四、课后习题序…...
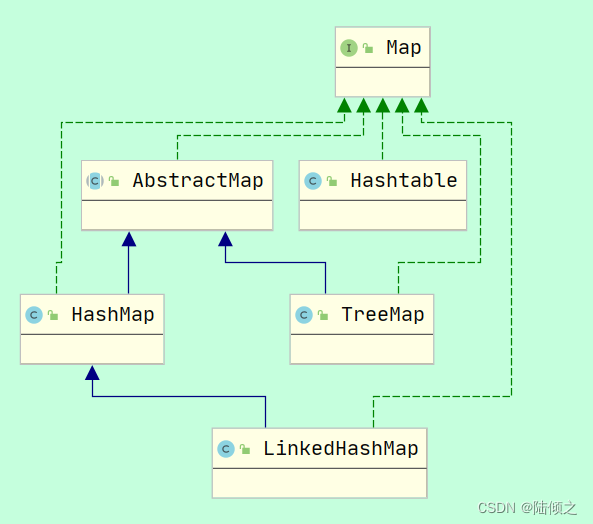
Map集合
Map集合 Map接口的简介 Map用于保存具有映射关系的数据,Map里保存着两组数据:key和value,它们都可以使任何引用类型的数据,但key不能重复。所以通过指定的key就可以取出对应的value。 Map 没有继承 Collection 接口,…...
PyQt5编程扩展 3.2 资源文件的使用
目录 本例运行效果: 设计Qt窗体 建立项目 放一个Group Box 放三个Label 放一个Horizontal Slider 放两个Line Edit 层次结构 布局 放一个Group Box 放两个Label 放两个Line Edit 放一个Push Button 层次结构 布局 放一个frame 层次结构 布局 窗体…...

Linux系统之文件共享目录设置方法
Linux系统之文件共享目录设置方法一、本次实践目的二、检查本地系统环境1.检查系统版本2.检查系统内核三、创建相关用户及用户组1.创建共享目录2.创建测试用户账号3.创建用户组4.设置用户的属组5.查看admin和IT用户组成员6.查看所有用户信息四、共享目录权限设置1.设置/data/so…...
上海亚商投顾:三大指数均涨超1% 芯片板块集体大涨
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。市场情绪三大指数今日低开高走,午后集体涨超1%,创业板指盘中涨超1.7%。芯片板块集体大涨,…...

Harbor私有仓库部署与管理
目录 前言 一、Harbor概述 二、Harbor 的特性 三、Harbor的构成 四、Harbor构建Docker私有仓库 1、环境配置 2、案例需求 3、部署Harbor服务 3.1、部署docker compose服务 3.2 下载或上传Harbor安装程序 3.3、启动Harbor 3.4、查看Harbor启动镜像 4、物理机访问se…...

互联网架构之 “高可用” 详解
一、什么是高可用 高可用HA(High Availability)是分布式系统架构设计中必须考虑的因素之一,它通常是指,通过设计减少系统不能提供服务的时间。 假设系统一直能够提供服务,我们说系统的可用性是100%。 如果系统每运行…...
分布式高级篇4 —— 商城业务(2)
一、订单服务1、订单基本概念2、订单基本构成3、订单状态4、订单流程5、配置拦截器拦截订单请求6、订单确认页模型抽取7、订单确认页vo封装8、Feign 远程调用请求头丢失问题\*\*\*\*\* 惨痛教训9、Feign 异步调用请求头丢失问题10、查看库存状态11、模拟计算运费12、接口幂等性…...

二分查找基本原理
二分查找基本原理1.二分查找1.1 基本概念1.2 二分查找查找步骤1.2.1 中间索引不能整除,取整数作为中间索引1.2.2 索引不能整除,整数1作为中间索引1.3 二分查找大O记法表示2. 二分查找代码实现1.二分查找 1.1 基本概念 二分法(折半查找)是一…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
