贝叶斯学习
贝叶斯
- 贝叶斯学习的背景
- 贝叶斯定理
- 举例
- 概览
- 选择假设— MAP
- MAP举例
- 选择假设 — 极大似然 ML
- ML 举例: 抛硬币问题
- 极大似然 & 最小二乘
- Naïve Bayesian Classifier (朴素贝叶斯分类器)
- 举例1:词义消歧 (Word Sense Disambiguation)
- 举例 2: 垃圾邮件过滤
- 从垃圾邮件过滤中学到的经验
- MDL (最小描述长度,Minimum Description Length)
- MDL解释(基于信息理论)
- MDL 和 MAP
- 对MDL的另一个解释
- 总结
贝叶斯学习的背景
- 发现两件事情之间的关系 (因果分析, 先决条件 &结论) • 在我们的日常生活中,医生的疾病诊断可以被认为是一个贝叶斯学习过程
- A → B A \rightarrow B A→B
- e.g. 肺炎 → \rightarrow → 肺癌?
- 很难直接判断
- 反向思考
- e.g. 有多少肺癌患者曾经得过肺炎?

- e.g. 有多少肺癌患者曾经得过肺炎?
贝叶斯定理

P ( h ∣ D ) = P ( D ∣ h ) P ( h ) P ( D ) P(h|D) = \frac{P(D|h)P(h)}{P(D)} P(h∣D)=P(D)P(D∣h)P(h)
举例: 某项化验测试结果与癌症诊断
- P(h|D) = h的后验概率(posterior probability)
P(h|D) : 已知测试结果=‘+’, 那么得了这种癌症的概率- P(h) = h的先验概率(prior probability)
P(h) : 得这种癌症的概率- P(D)=D的先验概率
P(D):测试结果 = ‘+’的概率- P(D|h) = 给定 h 情况下 D 的概率
P(D|h):已知一个人得了这种癌症,那么测试结果为‘+’的概率
- P(h)
- 假设: 互相排斥的
- H假设空间: 完全详尽 ∑ P ( h i ) = 1 \sum P(h_i)=1 ∑P(hi)=1
- P(D)
- D:所有可能数据中的一个采样集合
- 与h相互独立
- 在比较不同假设时可以忽略
- P(D|h) (似然度 likelihood)
-
- log likelihood log(P(D|h)
举例
- 化验测试结果: +,患有某种癌症?
P ( c a n c e r ∣ + ) = ? P(cancer|+)=? P(cancer∣+)=?
我们已知:
- 正确的阳性样本: 98% (患有该癌症, 测试结果为 +)
- 正确的阴性样本: 97% (未患该癌症, 测试结果为 -)
- 在整个人群中,只有0.008 的人患这种癌症
P ( c a n c e r ∣ + ) = P ( + ∣ c a n c e r ) P ( c a n c e r ) / P ( + ) = 0.98 ∗ 0.008 / ( 0.98 ∗ 0.008 + 0.03 ∗ 0.992 ) = 0.21 P(cancer | + ) = P(+| cancer) P(cancer) / P(+) = 0.98*0.008/(0.98*0.008+0.03*0.992)= 0.21 P(cancer∣+)=P(+∣cancer)P(cancer)/P(+)=0.98∗0.008/(0.98∗0.008+0.03∗0.992)=0.21
P ( c a n c e r ) = 0.008 P(cancer) = 0.008 P(cancer)=0.008
P ( ¬ c a n c e r ) = 0.992 P(\neg cancer) = 0.992 P(¬cancer)=0.992
概览
- 贝叶斯定理
- 用先验概率来推断后验概率
- M a x A P o s t e r i o r , M A P , h M A P ,极大后验假设 Max\ A\ Posterior, MAP, h_{MAP} ,极大后验假设 Max A Posterior,MAP,hMAP,极大后验假设
- M a x i m u m L i k e l i h o o d , M L , h M L , 极大似然假设 Maximum Likelihood, ML, h_{ML}, 极大似然假设 MaximumLikelihood,ML,hML,极大似然假设
- • ML vs. LSE (最小二乘,Least Square Error)
- Naïve Bayes, NB, 朴素贝叶斯
- 独立属性/特征假设
- NB vs. MAP
- Maximum description length, MDL (最小描述长度)
- 权衡: 假设复杂度 vs. 假设带来的错误
- MDL vs. MAP
选择假设— MAP
P ( h ∣ D ) = P ( D ∣ h ) P ( h ) P ( D ) P(h|D) = \frac{P(D|h)P(h)}{P(D)} P(h∣D)=P(D)P(D∣h)P(h)
- 一般我们需要在给定训练集上最有可能的假设
- Maximum A Posteriori (MAP): (极大后验假设) hMA
h M A P = a r g m a x h ∈ H P ( h ∣ D ) P ( h ) = a r g m a x h ∈ H P ( D ∣ h ) P ( h ) P ( D ) = a r g m a x h ∈ H P ( D ∣ h ) P ( h ) \begin{align*} h_{MAP} &= \underset{h \in H}{argmax}P(h|D)P(h) \\ &= \underset{h \in H}{argmax} \frac{P(D|h)P(h)}{P(D)} \\ &= \underset{h \in H}{argmax}P(D|h)P(h) \end{align*} hMAP=h∈HargmaxP(h∣D)P(h)=h∈HargmaxP(D)P(D∣h)P(h)=h∈HargmaxP(D∣h)P(h)
MAP举例
-
实验室测试结果: +,患有某种特定癌症?
-
当我们已知:
- 正确的阳性: 98% (患癌, 检测结果 +)
- 正确的阴性: 97% (不患癌, 检测结果 -)
- 在整个人群中,只有 0.008 患有癌症
a r g m a x h ∈ H P ( D ∣ h ) P ( h ) \underset{h \in H}{argmax}P(D|h)P(h) h∈HargmaxP(D∣h)P(h)
P ( + ∣ c a n c e r ) P ( c a n c e r ) = 0.0078 , P ( + ∣ ¬ c a n c e r ) P ( ¬ c a n c e r ) = 0.0298 P(+|cancer)P(cancer) =0.0078, P(+|\neg cancer)P(\neg cancer) = 0.0298 P(+∣cancer)P(cancer)=0.0078,P(+∣¬cancer)P(¬cancer)=0.0298
h M A P = ¬ c a n c e r h_{MAP}= \neg cancer hMAP=¬cancer
P ( c a n c e r ) = 0.008 P ( ¬ c a n c e r ) = 0.992 P ( + ∣ c a n c e r ) = 0.98 P ( − ∣ c a n c e r ) = 0.02 P ( + ∣ ¬ c a n c e r ) = 0.03 P ( − ∣ ¬ c a n c e r ) = 0.97 \begin{align*} P(cancer) = 0.008 \ \ \ \ &P(\neg cancer)=0.992 \\ P(+|cancer) = 0.98 \ \ \ \ &P(-|cancer) = 0.02 \\ P(+|\neg cancer) = 0.03 \ \ \ \ &P(-|\neg cancer) = 0.97 \\ \end{align*} P(cancer)=0.008 P(+∣cancer)=0.98 P(+∣¬cancer)=0.03 P(¬cancer)=0.992P(−∣cancer)=0.02P(−∣¬cancer)=0.97选择假设 — 极大似然 ML
h M A P = a r g m a x h ∈ H P ( D ∣ h ) P ( h ) h_{MAP} = \underset {h \in H}{argmax}P(D|h)P(h) hMAP=h∈HargmaxP(D∣h)P(h)

如果知道P(h),聪明的人总是能最大限度地从经验中学习 -
如果我们完全不知道假设的概率分布,或者我们知道所有的假设发生的概率相同,那么MAP 等价于 Maximum Likelihood (hML 极大似然假设)
h M L = a r g m a x h i i n H P ( D ∣ h i ) h_{ML} = \underset{h_i in H}{argmax}P(D|h_i) hML=hiinHargmaxP(D∣hi)
ML 举例: 抛硬币问题
- 2 个硬币: P1(H) = p,P2(H) = q
- 抛1号硬币的概率是 a
- 但是 a, p, q 未知的
- 观察到一些产生序列:
- 2HHHT,1HTHT, 2HHHT, 2HTTH
- 估计 a, p, q 最有可能的值
- “简单” 估计: ML (maximum likelihood,极大似然)
- 抛一个(p,1-p)硬币 m 次,得到k 次 H 和 m-k 次 T
l o g L ( D ∣ p ) = l o g P ( D ∣ p ) = l o g ( p k ( 1 − p ) m − k ) = k l o g p + ( m − k ) l o g ( 1 − p ) \begin{align*} logL(D|p) &= logP(D|p) \\ &=log(p^k(1-p)^{m-k} )\\ &=klogp+(m-k)log(1-p) \\ \end{align*} logL(D∣p)=logP(D∣p)=log(pk(1−p)m−k)=klogp+(m−k)log(1−p)- 求最大值,对 p 求导令导数为 0: d ( l o g L ( D ∣ p ) ) d p = k p − m − k 1 − p = 0 \frac{d(logL(D|p))}{dp} = \frac{k}{p} - \frac{m-k}{1-p} = 0 dpd(logL(D∣p))=pk−1−pm−k=0
- 求解 p,得到: p = k / m p=k/m p=k/m
• 估计 a, p, q 最有可能的值
a = 1/4, p = 2/4, q = 8/12
极大似然 & 最小二乘

- 训练数据: < x i , d i > <x_i,d_i> <xi,di>
- d i = f ( x i ) + e i d_i = f(x_i) + e_i di=f(xi)+ei
- di : 独立的样本.
- f(xi): 没有噪声的目标函数值
- ei: 噪声,独立随机变量,正态分布 N ( 0 , σ 2 ) N(0, σ^2) N(0,σ2)
- → \rightarrow → di : 正态分布 N ( f ( x i ) , σ 2 ) N(f(x_i),\sigma ^2) N(f(xi),σ2)


- 独立随机变量,正态分布噪声 N ( 0 , σ 2 ) , h M L = h L S E N(0, \sigma^2), h_{ML} =h_{LSE} N(0,σ2),hML=hLSE
Naïve Bayesian Classifier (朴素贝叶斯分类器)
- 假设目标函数 f : X → V X \rightarrow V X→V,其中每个样本 x = (a1, a2, …, an). 那么最有可能的 f(x) 的值是:
v M A P = a r g m a x v j ∈ V P ( x ∣ v j ) P ( v j ) v_{MAP} = \underset {v_j \in V}{argmax}P(x|v_j)P(v_j) vMAP=vj∈VargmaxP(x∣vj)P(vj) - 朴素贝叶斯假设:
P ( x ∣ v j ) = P ( a 1 , a 2 . . . a n ∣ v j ) = ∏ i P ( a i ∣ v j ) P(x|v_j)=P(a_1,a_2...a_n|v_j)=\prod_iP(a_i|v_j) P(x∣vj)=P(a1,a2...an∣vj)=i∏P(ai∣vj)
每个属性 a 1 , a 2 . . . a n 独立 每个属性a_1,a_2...a_n独立 每个属性a1,a2...an独立 - 朴素贝叶斯分类器:
v N B = P v j ∈ V ( v j ) ∏ i P ( a i ∣ v j ) = a r g m a x v j ∈ V { l o g P ( v j ) + ∑ i l o g P ( a i ∣ v j ) } \begin{align*} v_{NB} &= \underset{v_j \in V}P(v_j)\prod_iP(a_i|v_j) \\ &=\underset{v_j \in V}{argmax}\{logP(v_j) + \sum_ilogP(a_i|v_j)\} \\ \end{align*} vNB=vj∈VP(vj)i∏P(ai∣vj)=vj∈Vargmax{logP(vj)+i∑logP(ai∣vj)}
如果满足属性之间的独立性,那么 v M A P = v N B v_{MAP} = v_{NB} vMAP=vNB
举例1:词义消歧 (Word Sense Disambiguation)
- e.g. fly =? bank = ?
- 对于单词 w,使用上下文 c 进行词义消歧
- e.g. A fly flies into the kitchen while he fry the chicken. (他在炸鸡时一只苍蝇飞进了厨房)
- 上下文 c: 在词 w 周围的一组词wi(即:特征 / 属性)
- si: 词 w 的第 ith 个含义(即:输出标签)
- 朴素贝叶斯假设: P ( c ∣ s k ) = ∏ w i ∈ c P ( w i ∣ s k ) P(c|s_k)=\prod_{w_i \in c}P(w_i|s_k) P(c∣sk)=wi∈c∏P(wi∣sk)
- 朴素贝叶斯选择: s = a r g m a x s k { l o g P ( s k ) + ∑ w i ∈ c l o g P ( w i ∣ s k ) } s=\underset{s_k}{argmax}\{logP(s_k) + \sum_{w_i \in c}logP(w_i|s_k)\} s=skargmax{logP(sk)+wi∈c∑logP(wi∣sk)}
其中: P ( s k ) = C ( s k ) C ( w ) P ( w i ∣ s k ) = C ( w i , s k ) C ( s k ) P(s_k) = \frac{C(s_k)}{C(w)}\ \ \ \ \ P(w_i|s_k) = \frac{C(w_i,s_k)}{C(s_k)} P(sk)=C(w)C(sk) P(wi∣sk)=C(sk)C(wi,sk)
举例 2: 垃圾邮件过滤

- 垃圾邮件量: 900亿/天,80% 来自 <200 发送者
- 第四季度主要垃圾邮件来源 (数据来自 Sophos)
- 美国 (21.3% 垃圾信息来源,较28.4%有所下降)
- 俄罗斯 (8.3%, 较 4.4% 有上升)
- 中国 (4.2%, 较 4.9% 有下降)
- 巴西 (4.0%, 较 3.7% 有上升)
垃圾邮件过滤问题中人们学到的经验:
- 不要武断地忽略任何信息
- E.g. 邮件头信息
- 不同的代价: 假阳性 v.s. 假阴性
- 一个非常好的参考报告: http://www.paulgraham.com/better.html
从垃圾邮件过滤中学到的经验
(根据报告:)
早期关于贝叶斯垃圾邮件过滤的论文有两篇,于1998年发表在同一个会议

1) 作者是 Pantel 和 Lin; 2) Microsoft 研究院的一个小组
Pantel 和 Lin的过滤方法效果更好
但它只能捕捉92%的垃圾邮件,且有1.16% 假阳性错误
文章作者实现了一个贝叶斯垃圾邮件过滤器
它 能捕捉 99.5%的垃圾邮件 且 假阳性错误低于0.03%
Subject*FREE 0.9999
Subject*free 0.9782,
free 0.6546
free!! 0.9999
- 5 处不同
- 他们训练过滤器的数据非常少:
- 160 垃圾邮件和466非垃圾邮件
2.最重要的一个不同可能是他们忽略了邮件头
3.Pantel 和 Lin 对词进行了stemming (词干化) —— 做法有些草率了
4.计算概率的方式不同。他们使用了全部的词,但作者只用了最显著的15个词
5.他们没有对假阳性做偏置。而作者考虑了:对非垃圾邮件中出现的词频翻倍
- 160 垃圾邮件和466非垃圾邮件
MDL (最小描述长度,Minimum Description Length)
- 奥卡姆剃刀:
- 偏向于最短的假设
- MDL:
- 偏向假设 h 使得最小化: h M D L = a r g m i n h ∈ H { L C 1 ( h ) + L C 2 ( D ∣ h ) } h_{MDL}=\underset{h \in H}{argmin}\{L_{C_1}(h) + L_{C_2}(D|h)\} hMDL=h∈Hargmin{LC1(h)+LC2(D∣h)}
其中 L C ( x ) L_C(x) LC(x)是 x在编码C下的 描述长度
- 偏向假设 h 使得最小化: h M D L = a r g m i n h ∈ H { L C 1 ( h ) + L C 2 ( D ∣ h ) } h_{MDL}=\underset{h \in H}{argmin}\{L_{C_1}(h) + L_{C_2}(D|h)\} hMDL=h∈Hargmin{LC1(h)+LC2(D∣h)}
MDL解释(基于信息理论)
- 为随机发送的信息所设计的编码
- 遇到消息 i 的概率是 pi
- 所需的最短编码(最小期望传输位数)是什么?
- 为可能性较大的消息赋予较短的编码

- 为可能性较大的消息赋予较短的编码
- 最优编码对消息i 的编码长度为 -log2 p 比特 [Shannon & Weaver 1949]

MDL 和 MAP
-log2 p (h): 假设空间H最优编码下,h 的长度
-log2 p (D|h): 最优编码下,给定h 时D 的描述长度

对MDL的另一个解释
h M D L = a r g m i n h ∈ H { L C 1 ( h ) + L C 2 ( D ∣ h ) } h_{MDL} = \underset {h \in H}{argmin}\{L_{C_1}(h) + L_{C_2}(D|h)\} hMDL=h∈Hargmin{LC1(h)+LC2(D∣h)}
-
h的长度 和 给定h编码数据的代价
- 假设实例的序列以及编码规则对发送者和接收者来说都是已知的
- 没有分类错误: 除h外不需要传输额外的信息
- 如果 h 错误分类了某些样本,则需要传输:
-
- **哪个实例出错了? **
– 最多 log2m (m: 实例的个数)
- **哪个实例出错了? **
-
- **正确的分类结果是什么? **
– 最多 log2k (k: 类别的个数)
- **正确的分类结果是什么? **
-
-
权衡: 假设的复杂程度 vs. 由假设造成的错误数
- 更偏好 一个短的且错误更少的假设
而不是一个长的但完美分类训练数据的假设

- 更偏好 一个短的且错误更少的假设
总结
- 贝叶斯定理
- 用先验概率来推断后验概率
- M a x A P o s t e r i o r , M A P , h M A P ,极大后验假设 Max\ A\ Posterior, MAP, h_{MAP} ,极大后验假设 Max A Posterior,MAP,hMAP,极大后验假设
- M a x i m u m L i k e l i h o o d , M L , h M L , 极大似然假设 Maximum Likelihood, ML, h_{ML}, 极大似然假设 MaximumLikelihood,ML,hML,极大似然假设
- • ML vs. LSE (最小二乘,Least Square Error)
- Naïve Bayes, NB, 朴素贝叶斯
- 独立属性/特征假设
- NB vs. MAP
- Maximum description length, MDL (最小描述长度)
- 权衡: 假设复杂度 vs. 假设带来的错误
- MDL vs. MAP
相关文章:

贝叶斯学习
贝叶斯 贝叶斯学习的背景贝叶斯定理举例 概览选择假设— MAPMAP举例 选择假设 — 极大似然 MLML 举例: 抛硬币问题 极大似然 & 最小二乘Nave Bayesian Classifier (朴素贝叶斯分类器)举例1:词义消歧 (Word Sense Disambiguation)举例 2: 垃圾邮件过滤 从垃圾邮件…...

Java并发系列之六:CountDownLatch
CountDownLatch作为开发中最常用的组件,今天我们来聊聊它的作用以及内部构造。 首先尝试用一句话对CountDownLatch进行概括: CountDownLatch基于AQS,它实现了闩锁,在开发中可以将其用作任务计数器。 若想要较为系统地去理解这些特性ÿ…...

24数据结构-图的基本概念与存储结构
目录 第六章 图6.1 图的基本概念知识回顾 6.2 图的储存结构(邻接矩阵法)1. 数组表示法(1) 有向图,无向图的邻接矩阵 2. 定义邻接矩阵的结构3. 定义图的结构4. 构造图G5. 特点 第六章 图 6.1 图的基本概念 图是一种非线性结构 图的特点&am…...
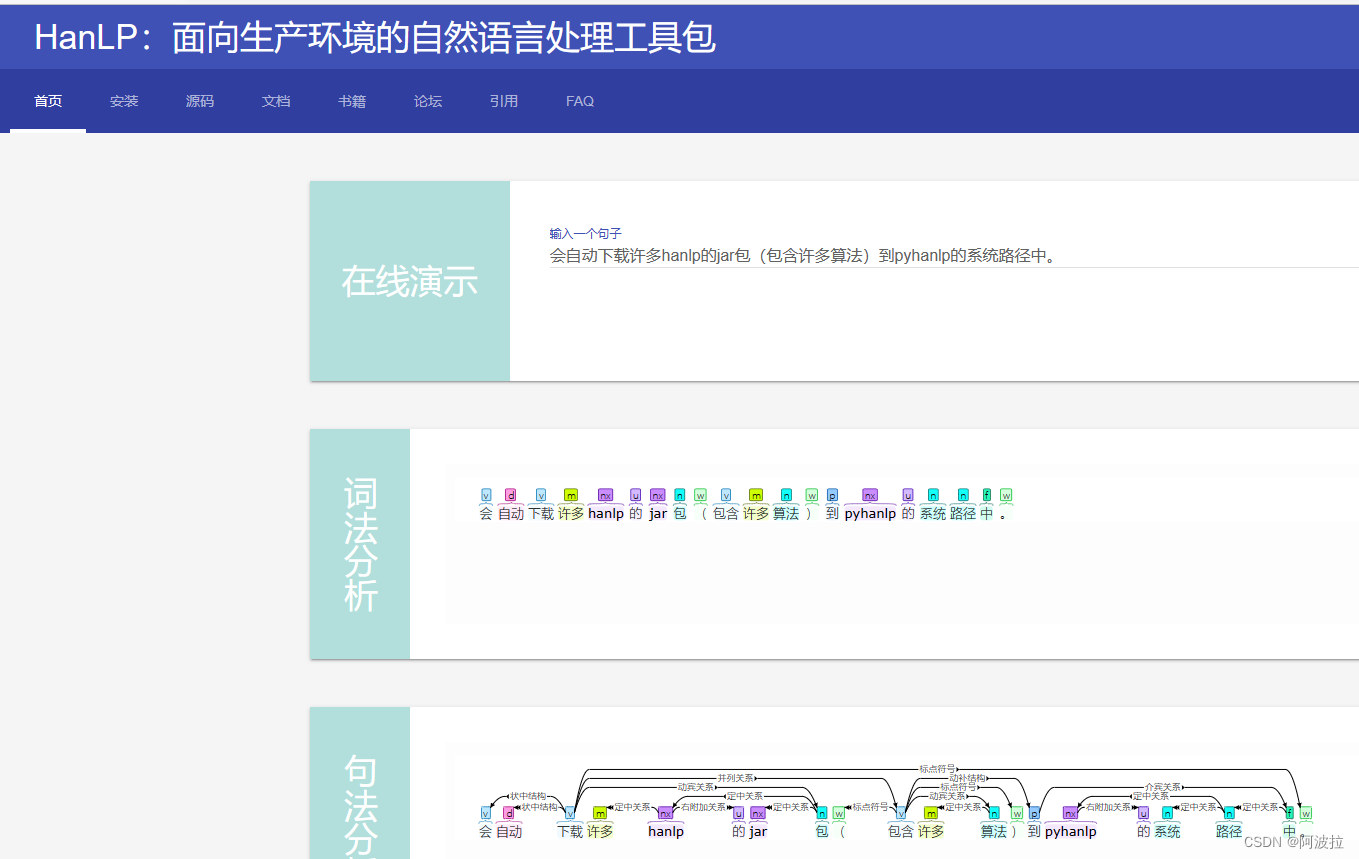
自然语言处理学习笔记(三)————HanLP安装与使用
目录 1.HanLP安装 2.HanLP使用 (1)预下载 (2)测试 (3)命令行 (4)测试样例 3.pyhanlp可视化 4. HanLP词性表 1.HanLP安装 HanLP的 Python接口由 pyhanlp包提供,其安装…...
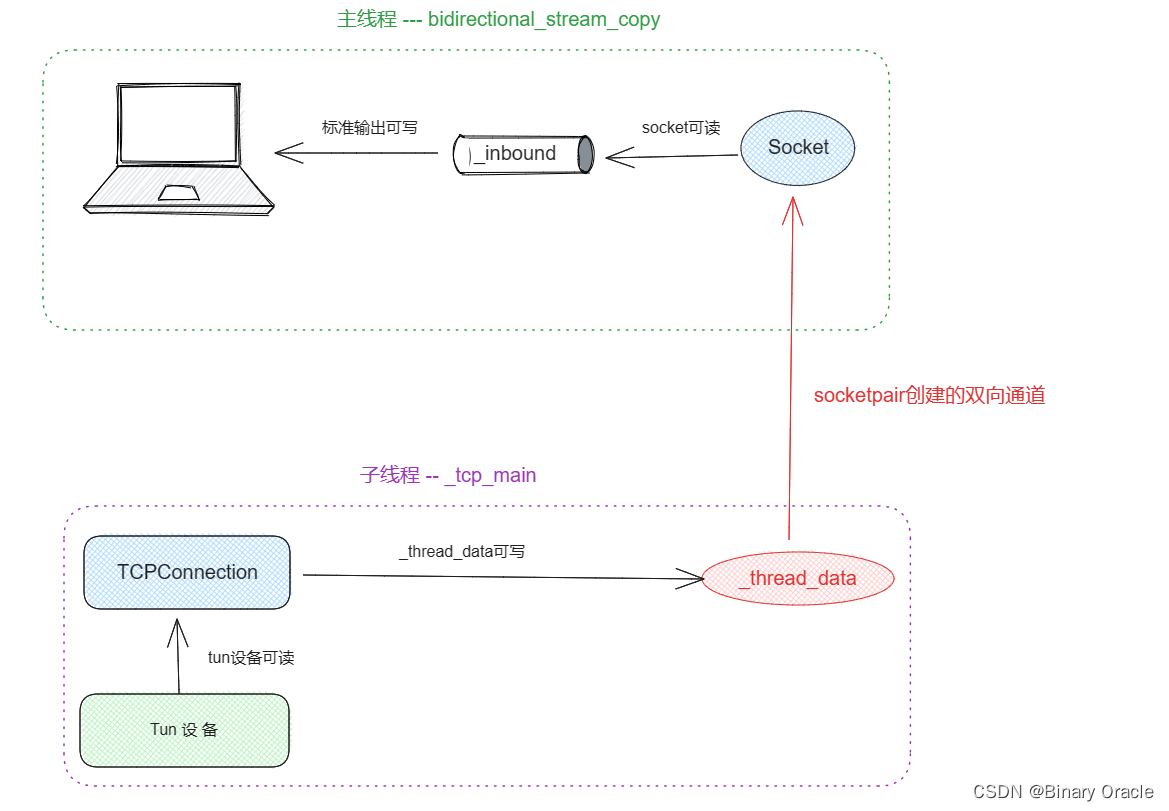
CS 144 Lab Five -- the network interface
CS 144 Lab Five -- the network interface TCP报文的数据传输方式地址解析协议 ARPARP攻击科普 Network Interface 具体实现测试tcp_ip_ethernet.ccTCPOverIPv4OverEthernetAdapterTCPOverIPv4OverEthernetSpongeSocket通信过程 对应课程视频: 【计算机网络】 斯坦福大学CS144…...

Mecha
一、Mecha Mecha 是一个开源的多云 Kubernetes 管理平台,旨在简化和统一在多个云提供商上运行 Kubernetes 集群的管理和操作。它是由阿里巴巴集团开发和维护的项目。 Mecha 的主要目标是提供一个统一的界面和工具,使用户能够更轻松地在不同的云提供商上…...

Apache RocketMQ之集成RocketMQ_MQTT 安装部署协议
Apache RocketMQ 安装说明 安装步骤 参考快速开始 https://rocketmq.apache.org/zh/docs/quickStart/01quickstart 安装可视化rocketmq_dashboard下载地址 https://rocketmq.apache.org/zh/docs/4.x/deployment/03Dashboard/ 安装rocketmq_mqtt https://rocketmq.apache.o…...

Oracle多行数据合并为一行数据,并将列数据转为字段名
Oracle多行数据合并为一行数据 实现查询效果原数据 方式一:MAX()数据效果SQL 方式二:LISTAGG()数据效果 方式三:WM_CONCAT()数据效果 实现查询效果 原数据 FZPROJECTVALUE1电脑$16001手机$121导管$12电脑$22手机$22 方式一:MAX…...
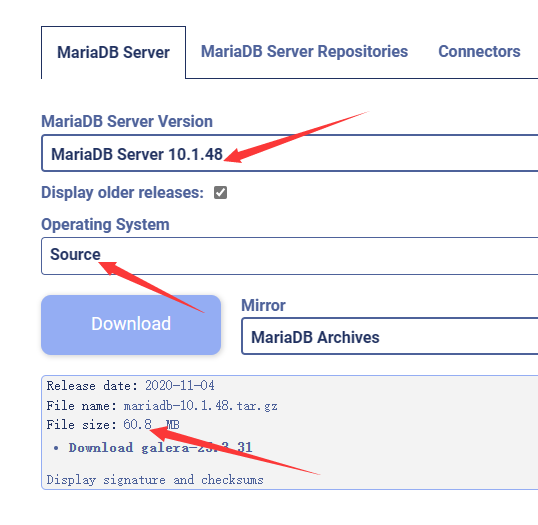
MySQL5.7 与 MariaDB10.1 审计插件兼容性验证
这是一篇关于发现 MariaDB 审计插件导致 MySQL 发生 crash 后,展开适配验证并进行故障处理的文章。 作者:官永强 爱可生DBA 团队成员,擅长 MySQL 运维方面的技能。热爱学习新知识,亦是个爱打游戏的宅男。 本文来源:原创…...

PyTorch Lightning教程五:Debug调试
如果遇到了这样一个问题,当一次训练模型花了好几天,结果突然在验证或测试的时候崩掉了,这个时候其实是很奔溃的,主要还是由于没有提前知道哪些时候会出现什么问题,本节会引入Lightning的Debug方案 1.fast_dev_run参数 …...

末流211无科研保研经验分享
文章目录 个人背景夏令营哈工大威海西工大光电北航软院北邮计算机中科大科学岛 预推免东南软件北航计算机 写在最后心路历程寄语 个人背景 院校:末流211专业背景:计算机科学与技术排名:夏令营7 / 126,预推免3 / 126英语ÿ…...

日期选择器多选换行
<el-form-item label"日期选择"><div class"multi-date-picker"><div class"date-item"><span class"dateIcon"><el-icon><Calendar /></el-icon></span><span class"dateIt…...
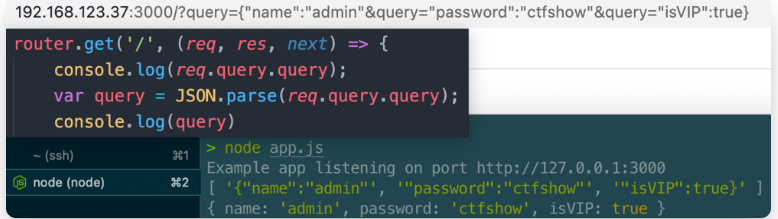
NodeJS原型链污染ctfshow_nodejs
文章目录 NodeJS原型链污染&ctfshow_nodejs前言0x01.原型与原型链0x02.prototype和__proto__分别是什么?0x03.原型链继承不同对象的原型链* 0x04.原型链污染原理0x05.merge()导致原型链污染0x06.ejs模板引擎RCEejs模板引擎另一处rce 0x07.jade模板引擎RCE【ctfs…...

18. SpringBoot 如何在 POM 中引入本地 JAR 包
❤️ 个人主页:水滴技术 🌸 订阅专栏:成功解决 BUG 合集 🚀 支持水滴:点赞👍 收藏⭐ 留言💬 Spring Boot 是一种基于 Spring 框架的轻量级应用程序开发框架,它提供了快速开发应用程…...
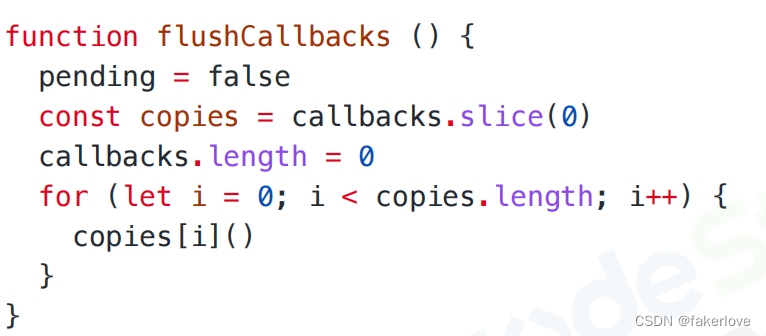
vue2-$nextTick有什么作用?
1、$nextTick是什么? 官方定义:在下次DOM更新循环结束之后执行延迟回调。在修改数据之后立即使用这个方法,获取更新后的DOM。 解释:Vue在更新DOM时是异步执行的,当数据发生变化时,Vue将开启一个异步更新的队…...
python自动收集粘贴板
win10的粘贴板可以用“winV”查看: 每次复制都相当于入栈一个字符串,粘贴相当于获取栈顶。 但是系统自带的这个粘贴板貌似不能一键导出,所以我写了个python代码完成这个功能: import pyperclip import timetmp while True:txt…...
Vue3_语法糖—— <script setup>以及unplugin-auto-import自动引入插件
<script setup>import { ref , onMounted} from vue;let obj ref({a: 1,b: 2,}); let changeObj ()>{console.log(obj)obj.value.c 3 //ref写法}onMounted(()>{console.log(obj)})</script> 里面的代码会被编译成组件 setup() 函数的内容。 相当于 <…...

2023-08-06力扣做过了的题
链接: 剑指 Offer 30. 包含min函数的栈 题意: 如题 解: 初级算法里做过的题 优化是存储和min的差值使得只需要n的栈和一个int min 实际代码: #include<bits/stdc.h> using namespace std; class MinStack { public:…...

进程间通信之管道
文章目录 一、管道1. 匿名管道2. 命名管道 进程具有独立性,因此进程间通信的前提是两个进程能看到同一份资源 一、管道 对于进程打开的内存文件,操作系统是以引用计数的方式创建的 file 结构体,如果让两个进程与同一个 file 结构体关联&…...
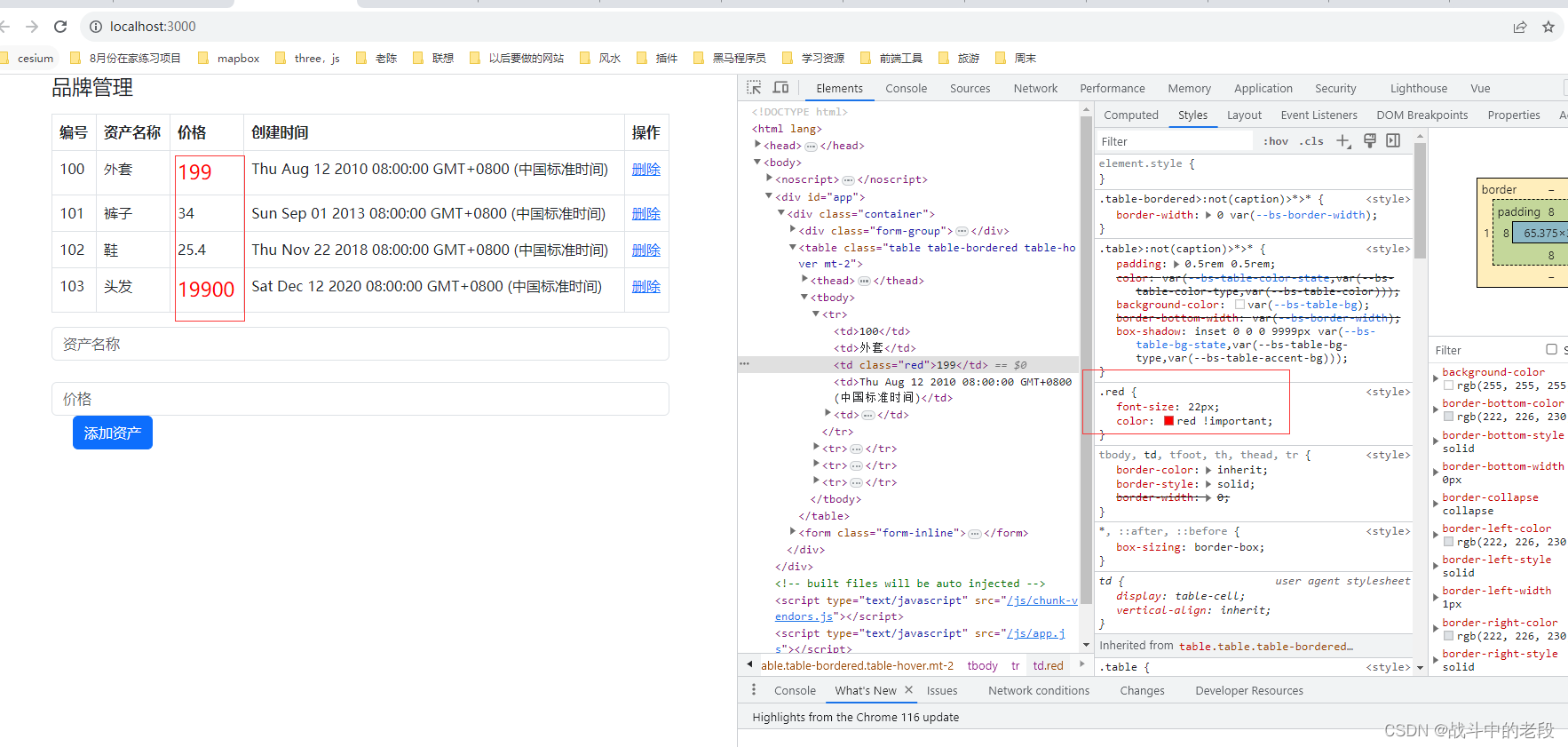
f12 CSS网页调试_css样式被划了黑线怎么办
我的问题是这样的 class加上去了,但是样式不生效,此时可能是样式被其他样式覆盖了, 解决方案就是 给颜色后边添加一个!important...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
