线性规划和单纯形法-原理篇
文章目录
- 引言
- 线性规划标准型
- 问题特点
- 单纯形法
引言
很多运筹学的教材都是从线性规划开始的,我平时做算法策略的落地应用时也研发了一部分基于线性规划的技术方案。可以说,如果搞不懂线性规划,很难成为一名优秀的运筹优化算法工程师。
但是我在体系化学习时,却先在其他地方转了一大圈,才来到这里。
主要原因是,这线性规划的原理着实有点难,之前看了很多遍,总有种好像懂了但又没完全懂的挫败感。痛定思痛下终于决定,还是从最简单的无约束问题开始,然后逐渐过渡到有约束问题,以及现在的线性规划问题。
针对无约束优化问题,我细分为一维问题和多维问题,并分别学习了适合解决一维问题的黄金分割法、切线法和进退法等,以及用于解决多维问题的坐标轮转法、最速下降法和拟牛顿法等;针对约束优化问题,相继学习了拉格朗日乘子法和罚函数法。
线性规划问题本质上是一类特殊的约束优化问题,这类优化问题在实际场景中十分常见,同时由于问题的特殊性,也给问题的高效求解带来了新思路。
前面提到过,线性规划对我来说挺难的,只用一篇文章是很难讲清楚。所以打算分成上下两篇:本篇着重讲明白算法原理,下一篇着重研究实践应用。
必须要预警的是,后续内容很枯燥,因为夹杂着非常多的证明和推理过程。我愿意花大量时间在这上面,是希望不仅能知其然,还能知其所以然。不想看细节过程的,可以更多关注整体的逻辑框架:线性规划问题相比一般约束问题的特殊性在哪里–>该特殊性使得线性规划问题具有哪些特点–>基于这些特点,所设计的算法(单纯形法)是如何实现高效求解的。
线性规划标准型
线性规划的标准型矩阵形式为
m i n f ( x ) = c T x s.t. A x = b x ≥ 0 min \quad f(\pmb x)=\pmb c^T\pmb x \\ \text{s.t.} \quad \pmb A\pmb x=\pmb b \\ \quad \quad \ \pmb x ≥ 0 minf(x)=cTxs.t.Ax=b x≥0
也可以写成分量形式
m i n f ( x ) = ∑ j = 1 n c j x j s.t. ∑ j = 1 n a i j x j = b i , i = 1 , 2 , . . . , m x j ≥ 0 , j = 1 , 2 , . . . , n min \quad f(x)=\sum_{j=1}^nc_jx_j \\ \text{s.t.} \quad \sum_{j=1}^na_{ij}x_j=b_i, \quad i=1,2,...,m \\ \quad x_j ≥0 ,\quad j=1,2,...,n\\ minf(x)=j=1∑ncjxjs.t.j=1∑naijxj=bi,i=1,2,...,mxj≥0,j=1,2,...,n
从定义上可以看出,相比一般的约束优化问题,线性规划问题在目标函数、约束条件和变量范围方面都增加了限制:(1)目标函数为线性加和的表达式;(2)约束条件只有线性等式;(3)优化变量大于等于0。
问题特点
增加了上述限制后的线性规划问题,具有哪些特点呢?
先说结论:问题的可行域为凸集–>最优解在凸集的顶点上–>顶点和基本可行解一一对应。
接下来逐个详细说明(证明)。
(1)可行域为凸集。
既然提到凸集,就需要先定义清楚凸集的含义:设 S ∈ R n S \in R^n S∈Rn是 n n n维欧式空间中的一个点集,若对于 x 1 ∈ S , x 2 ∈ S , x 1 ≠ x 2 x_1\in S, x_2 \in S,x_1≠x_2 x1∈S,x2∈S,x1=x2,以及任意 λ ∈ [ 0 , 1 ] \lambda\in [0, 1] λ∈[0,1],必有
λ x 1 + ( 1 − λ ) x 2 ∈ S \lambda x_1+(1-\lambda)x_2 \in S λx1+(1−λ)x2∈S
则称 S S S为凸集。
以下是凸集和非凸集的实例

对于线性规划问题,根据标准型约束的定义
A x 1 = b , x 1 ≥ 0 A x 2 = b , x 2 ≥ 0 \pmb A\pmb x_1=\pmb b, \pmb x_1 ≥ 0\\ \pmb A\pmb x_2=\pmb b, \pmb x_2 ≥ 0 Ax1=b,x1≥0Ax2=b,x2≥0
那么,针对任意 λ ∈ [ 0 , 1 ] \lambda\in[0, 1] λ∈[0,1],假设新变量 x = λ x 1 + ( 1 − λ ) x 2 \pmb x=\lambda \pmb x_1+(1-\lambda)\pmb x_2 x=λx1+(1−λ)x2,可做如下推导
A [ λ x 1 + ( 1 − λ ) x 2 ] = λ A x 1 + ( 1 − λ ) A x 2 = λ b + ( 1 − λ ) b = b \pmb A[\lambda \pmb x_1+(1-\lambda)\pmb x_2]=\lambda \pmb A\pmb x_1+(1-\lambda)\pmb A\pmb x_2=\lambda \pmb b + (1-\lambda) \pmb b=\pmb b A[λx1+(1−λ)x2]=λAx1+(1−λ)Ax2=λb+(1−λ)b=b
即等式约束成立。
由于 x 1 , x 2 , λ ≥ 0 \pmb x_1,\pmb x_2,\lambda≥0 x1,x2,λ≥0,下式显然也成立
λ x 1 + ( 1 − λ ) x 2 ≥ 0 \lambda \pmb x_1+(1-\lambda)\pmb x_2≥0 λx1+(1−λ)x2≥0
即 x \pmb x x大于等于0亦成立。
所以 x \pmb x x也在可行域内。根据凸集定义,线性规划问题的可行域就是个凸集。
可行域是凸集,有什么好处呢——看下一条结论。
(2)最优值一定在凸集的某个顶点上达到。
顶点这个词在物理世界很容易理解,但为了后续推导,还是需要用数学语言描述清楚这一概念:针对可行域内的 x \pmb x x,如果不存在 λ , x 1 ∈ S , x 2 ∈ S , x 1 ≠ x 2 \lambda,\pmb x_1\in S,\pmb x_2 \in S,\pmb x_1≠\pmb x_2 λ,x1∈S,x2∈S,x1=x2,使得
x = λ x 1 + ( 1 − λ ) x 2 \pmb x=\lambda \pmb x_1+ (1-\lambda)\pmb x_2 x=λx1+(1−λ)x2
则这个 x \pmb x x为凸集上的顶点。
要证明以上结论,此处使用反证法。
假设凸集的顶点为 x 1 , x 2 , . . . , x k \pmb x_1,\pmb x_2,...,\pmb x_k x1,x2,...,xk,最优解为 x ∗ \pmb x^\ast x∗。因为 x ∗ \pmb x^\ast x∗在可行域的凸集范围内,所以它可以由顶点表示为
x ∗ = ∑ i = 1 k λ i x i \pmb x^\ast=\sum_{i=1}^k\lambda_i\pmb x_i x∗=i=1∑kλixi
式中, λ i ≥ 0 \lambda_i≥0 λi≥0, ∑ i = 1 k λ i = 1 \sum_{i=1}^k\lambda_i=1 ∑i=1kλi=1。 x \pmb x x能被顶点通过线性组合的方式表示,很容易想象,但证明起来有些难,这里就不深入了,有兴趣的可以参考:多面集的表示定理。
上式两边同时左乘 c T \pmb c^T cT
c T x ∗ = ∑ i = 1 k λ i c T x i \pmb c^T\pmb x^\ast=\sum_{i=1}^k\lambda_i\pmb c^T\pmb x_i cTx∗=i=1∑kλicTxi
设 c T x s = min 1 ≤ i ≤ k c T x i \pmb c^T \pmb x_s= \mathop{\text{min}} \limits_{1≤i≤k} \pmb c^T \pmb x_i cTxs=1≤i≤kmincTxi,上式可以做如下推导
c T x ∗ = ∑ i = 1 k λ i c T x i ≥ ∑ i = 1 k λ i c T x s = c T x s ∑ i = 1 k λ i = c T x s \pmb c^T\pmb x^\ast=\sum_{i=1}^k\lambda_i\pmb c^T\pmb x_i≥\sum_{i=1}^k\lambda_i\pmb c^T\pmb x_s=\pmb c^T\pmb x_s\sum_{i=1}^k\lambda_i=\pmb c^T\pmb x_s cTx∗=i=1∑kλicTxi≥i=1∑kλicTxs=cTxsi=1∑kλi=cTxs
但由于 x ∗ \pmb x^\ast x∗是最优解,并且不在顶点上,所以
c T x ∗ < c T x s \pmb c^T\pmb x^\ast < \pmb c^T\pmb x_s cTx∗<cTxs
上述两式互相矛盾,所以假设不成立,即最优解必定在某个顶点上取到。
这个结论的最大优点在于,把决策空间从一个非常大的可行域空间收缩到了可行域的顶点上,而顶点的数量在大部分情况下是比较有限的,这就极大降低了问题求解的复杂度。
这里其实我还有个小疑惑,就是从证明过程来看,好像并不需要目标函数是线性的,是否说明即使目标函数是非线性表达式,最优解依然在顶点上取到?该疑惑目前暂未搞清楚,如有大佬,望不吝赐教。
(3)可行域凸集的顶点和基本可行解一一对应。
已经知道最优解在顶点上了,那顶点的数学表达式是怎样的呢?上述结论告诉我们,顶点就是基本可行解。
接下来,先看一下基本可行解的定义。
A \pmb A A是 m × n m\times n m×n的约束矩阵,可以从中取到一个非奇异方阵 B \pmb B B,然后把剩下列组成一个子阵 N \pmb N N,它们对应的 x \pmb x x分别表示为基变量 x B \pmb x_B xB和非基变量 x N \pmb x_N xN。等式约束可以表示为
B x b + N x N = b \pmb B\pmb x_b+\pmb N\pmb x_N=\pmb b Bxb+NxN=b
令 x N = 0 \pmb x_N=\pmb 0 xN=0,可以求出 x b = B − 1 b \pmb x_b=\pmb B^{-1}\pmb b xb=B−1b,组合 x b \pmb x_b xb和 x N \pmb x_N xN
x = ( B − 1 b , 0 ) T \pmb x=(\pmb B^{-1}\pmb b, 0)^T x=(B−1b,0)T
如果 B − 1 b ≥ 0 \pmb B^{-1}\pmb b≥0 B−1b≥0,则 x \pmb x x被称为基本可行解。
B \pmb B B的维度是 m × m m\times m m×m,理论上至多可以从任意 n n n列中随机选取 m m m列,所以 B \pmb B B的数量上限是 C n m C_n^m Cnm,即基本可行解的数量上限为 C n m C_n^m Cnm个。
上述结论需要分两步进行论证:(1)基本可行解都是顶点;(2)顶点都是基本可行解。
针对第一步,继续使用反证法。
假设某个基本可行解不是顶点,即存在可行解 x 1 , x 2 \pmb x_1,\pmb x_2 x1,x2和 λ ∈ [ 0 , 1 ] \lambda\in[0,1] λ∈[0,1],使得基本可行解 x \pmb x x可以表示为
x = λ x 1 + ( 1 − λ ) x 2 \pmb x=\lambda \pmb x_1+ (1-\lambda)\pmb x_2 x=λx1+(1−λ)x2
将 x \pmb x x写成基变量 x B \pmb x_B xB和非基变量 x N \pmb x_N xN两部分
x B = λ x 1 B + ( 1 − λ ) x 2 B \pmb x_B=\lambda \pmb x_{1B}+ (1-\lambda)\pmb x_{2B} xB=λx1B+(1−λ)x2B
x N = λ x 1 N + ( 1 − λ ) x 2 N \pmb x_N=\lambda \pmb x_{1N}+ (1-\lambda)\pmb x_{2N} xN=λx1N+(1−λ)x2N
x N \pmb x_N xN等式中,因为 x N = 0 , λ > 0 , 1 − λ > 0 , x 1 N ≥ 0 , x 2 N ≥ 0 \pmb x_N=0,\lambda>0,1-\lambda>0,\pmb x_{1N}≥0,\pmb x_{2N}≥0 xN=0,λ>0,1−λ>0,x1N≥0,x2N≥0,故
x N = x 1 N = x 2 N = 0 \pmb x_N=\pmb x_{1N}=\pmb x_{2N}=0 xN=x1N=x2N=0
所以 x 1 \pmb x_1 x1和 x 2 \pmb x_2 x2都是基本可行解,即
B x 1 B = b \pmb B\pmb x_{1B}=\pmb b Bx1B=b
B x 2 B = b \pmb B\pmb x_{2B}=\pmb b Bx2B=b
由于 B \pmb B B为非奇异方阵,所以 B x = b \pmb B\pmb x=\pmb b Bx=b有唯一解,所以
x B = x 1 B = x 2 B \pmb x_B=\pmb x_{1B}=\pmb x_{2B} xB=x1B=x2B
即 x 1 , x 2 \pmb x_1,\pmb x_2 x1,x2就是基本可行解 x \pmb x x,与基本假设不符,所以基本可行解必为可行解的顶点。
针对第二步,还是使用反证法。
假设 x \pmb x x是可行域的顶点,还是先拆解为非零项 x B \pmb x_B xB和零项 x N \pmb x_N xN
B x B = b \pmb B\pmb x_B=\pmb b BxB=b
但由于不是基本可行解,所以对应 B \pmb B B应该是线性相关的,即存在一组非0向量 w \pmb w w,使得
B w = 0 \pmb B\pmb w=\pmb 0 Bw=0
上式乘以系数 δ \delta δ,然后和上上式分别做加法和减法,得到
B ( x B + δ w ) = b B ( x B − δ w ) = b \pmb B(\pmb x_B+\delta \pmb w)=\pmb b\\ \pmb B(\pmb x_B-\delta \pmb w)=\pmb b B(xB+δw)=bB(xB−δw)=b
先令 x B 1 = x B + δ w , x B 2 = x B − δ w \pmb x_B^1=\pmb x_B+\delta \pmb w,\pmb x_B^2=\pmb x_B-\delta \pmb w xB1=xB+δw,xB2=xB−δw,再令 x 1 = ( x B 1 , 0 ) , x 2 = ( x B 2 , 0 ) \pmb x_1=(\pmb x_B^1, \pmb 0),\pmb x_2=(\pmb x_B^2, \pmb 0) x1=(xB1,0),x2=(xB2,0),首先可得
x = 1 2 x 1 + 1 2 x 2 \pmb x=\frac{1}{2}\pmb x_1+\frac{1}{2}\pmb x_2 x=21x1+21x2
同时只要 δ \delta δ足够小
x ± δ w > = 0 \pmb x\pm\delta \pmb w >=\pmb 0 x±δw>=0
即 x 1 \pmb x_1 x1和 x 2 \pmb x_2 x2都是可行解,这说明 x \pmb x x不能是顶点,两者矛盾,所以顶点也必定都是基本可行解。
有了该结论后,理论上,只要算出所有基本可行解的目标函数值,并返回最小值,即得到了最优解。但基本可行解的数量上限是 C n m C_n^m Cnm个,如果 n n n的数量比较大,用遍历的方式寻找最小值貌似就有些吃不消了。
此时大名鼎鼎的单纯形法就该登场了。
单纯形法
同样先给结论,单纯形法最厉害的地方在于:任意给定一个基本可行解后,通过简单的计算评估后,便可以告诉我们,该解是否还有改进空间,如果有,朝着哪个方向改进最好。这样的话,便不再需要去遍历所有基本可行解,所以能极大提升问题求解的效率。
假设已经得到一个基本可行解
x 0 = [ x B , 0 ] = [ B − 1 b , 0 ] \pmb x_0=[\pmb x_B,\pmb 0]=[\pmb B^{-1}\pmb b,\pmb 0] x0=[xB,0]=[B−1b,0]
对应的目标函数值为
f 0 = c B T B − 1 b f_0=\pmb c_B^T\pmb B^{-1}\pmb b f0=cBTB−1b
先把 x 0 \pmb x_0 x0写成基本可行解的通用表达式 [ x B , x N ] [\pmb x_B,\pmb x_N] [xB,xN],代入等式约束
B x B + N x N = b \pmb B\pmb x_B+\pmb N\pmb x_N=\pmb b BxB+NxN=b
移项, x B \pmb x_B xB可以表示为
x B = B − 1 b − B − 1 N x N \pmb x_B=\pmb B^{-1}\pmb b-\pmb B^{-1}\pmb N\pmb x_N xB=B−1b−B−1NxN
通用表达式结合上式后,再代入目标函数表达式
f = c B T ( B − 1 b − B − 1 N x N ) + c N T x N f=\pmb c_B^T(\pmb B^{-1}\pmb b-\pmb B^{-1}\pmb N\pmb x_N)+\pmb c_N^T\pmb x_N f=cBT(B−1b−B−1NxN)+cNTxN
重组一下
f = c B T B − 1 b − ( c B T B − 1 N − c N T ) x N f=\pmb c_B^T\pmb B^{-1}\pmb b-(\pmb c_B^T\pmb B^{-1}\pmb N-\pmb c_N^T)\pmb x_N f=cBTB−1b−(cBTB−1N−cNT)xN
上式可以描述为
f = f 0 − ∑ j ∈ R ( z j − c j ) x j f=f_0-\sum_{j\in R}(z_j-c_j)x_j f=f0−j∈R∑(zj−cj)xj
其中, R R R是非基变量集合, z = c B T B − 1 N \pmb z=\pmb c_B^T\pmb B^{-1}\pmb N z=cBTB−1N。
在当前的 x 0 \pmb x_0 x0中,由于 x j = 0 x_j=0 xj=0,即 f f f的后一项为0;所以目标函数能继续降低的基本条件是:至少存在一个 j j j,使得 z j − c j > 0 z_j-c_j>0 zj−cj>0,同时 x j x_j xj也能够从0增加为正数。
z j − c j z_j-c_j zj−cj是参数不是变量,是否存在大于0的 j j j,是无法改变的;但是 x j x_j xj的值理论上是可以优化的,当然该值也不能随意增大,其需要满足的约束是
x B = B − 1 b − B − 1 N x N ≥ 0 \pmb x_B=\pmb B^{-1}\pmb b-\pmb B^{-1}\pmb N\pmb x_N≥0 xB=B−1b−B−1NxN≥0
假设 x k ∈ x N x_k\in \pmb x_N xk∈xN,将从0变为正数(专业术语叫入基),为了保证基本可行解的要求, x B \pmb x_B xB中需要有一个值变为0(专业术语叫出基)
x B = [ x B 1 x B 2 ⋅ ⋅ ⋅ x B m ] = [ b ˉ 1 b ˉ 2 ⋅ ⋅ ⋅ b ˉ m ] − [ y 1 k y 2 k ⋅ ⋅ ⋅ y m k ] x k ≥ 0 \pmb x_B=\left [ \begin{matrix} x_{B1} \\ x_{B2} \\ ··· \\ x_{Bm} \\ \end{matrix} \right ]= \left [ \begin{matrix} \bar b_1 \\ \bar b_2 \\ ··· \\ \bar b_m \\ \end{matrix} \right ]- \left [ \begin{matrix} y_{1k} \\ y_{2k} \\ ··· \\ y_{mk} \\ \end{matrix} \right ]x_k≥0 xB= xB1xB2⋅⋅⋅xBm = bˉ1bˉ2⋅⋅⋅bˉm − y1ky2k⋅⋅⋅ymk xk≥0
其中, b ˉ = B − 1 b \pmb {\bar b}=\pmb B^{-1}\pmb b bˉ=B−1b, y k = B − 1 N k \pmb y_k=\pmb B^{-1}\pmb N_k yk=B−1Nk。为了保证 x B ≥ 0 \pmb x_B≥0 xB≥0, x k x_k xk的最优值是
x k = m i n { b ˉ 1 y 1 k , b ˉ 2 y 2 k , . . . , b ˉ m y m k } x_k=min\{\frac{\bar b_1}{y_{1k}},\frac{\bar b_2}{y_{2k}},...,\frac{\bar b_m}{y_{mk}}\} xk=min{y1kbˉ1,y2kbˉ2,...,ymkbˉm}
基于以上逻辑,我们可以描述为:如果存在 k k k,使得 z k − c k > 0 z_k-c_k>0 zk−ck>0,此时令 x k = m i n b ˉ i y i k x_k=min{\frac{\bar b_i}{y_{ik}}} xk=minyikbˉi,可以使得目标函数值得到最大程度的降低。
这里还有一些特殊情况需要单独考虑:
(1) 所有 z i − c i ≤ 0 z_i-c_i≤0 zi−ci≤0,即 f ≤ f 0 f≤f_0 f≤f0,此时当前基本可行解就是最优解。
(2) x k = m i n b ˉ i y i k x_k=min{\frac{\bar b_i}{y_{ik}}} xk=minyikbˉi中, b ˉ i \bar b_i bˉi是原基本可行解的分量,所以其值≥0是毋庸置疑的;但是 y i k y_{ik} yik的大小是不确定的,如果其部分值≤0,结合 x k ≥ 0 x_k≥0 xk≥0的自身约束,原有流程还能继续进行;但如果全部≤0,流程就无法再继续进行了,事实上,即使 x k x_k xk取无穷大, x B = b ˉ − y k x k ≥ 0 \pmb x_B=\pmb {\bar b}-\pmb y_kx_k≥0 xB=bˉ−ykxk≥0的约束依然能够满足, f f f将变为无穷小,所以此时原问题无下界,不存在最小值。
综上,单纯形法的基本步骤可以概述为:
(1) 将所给的线性规划问题化为标准型;
(2) 找出一个初始基本可行解。
(3) 检验 z i − c i z_i-c_i zi−ci和 b ˉ i y i k \frac{\bar b_i}{y_{ik}} yikbˉi,判断当前解的状态:最优解或不存在最优解,则退出;否则继续。
(4) 找到最佳 k k k,更新 x B \pmb x_B xB,得到一个新的基本可行解,转至(3)。
好了,总算是搞明白求解线性规划问题的算法原理了。
相关文章:

线性规划和单纯形法-原理篇
文章目录 引言线性规划标准型问题特点单纯形法 引言 很多运筹学的教材都是从线性规划开始的,我平时做算法策略的落地应用时也研发了一部分基于线性规划的技术方案。可以说,如果搞不懂线性规划,很难成为一名优秀的运筹优化算法工程师。 但是…...

FBX SDK开发快速上手指南
一段时间以来,我一直想制作一个 FBX Exporter 将 FBX 文件转换为我自己的格式。 整个过程不是很顺利,主要是FBX的官方文档不是很清楚。 另外,由于 FBX 格式被许多应用程序使用,而不仅仅是游戏引擎,因此提供的示例代码没…...

探讨|使用或不使用机器学习
动动发财的小手,点个赞吧! 机器学习擅长解决某些复杂问题,通常涉及特征和结果之间的困难关系,这些关系不能轻易地硬编码为启发式或 if-else 语句。然而,在决定 ML 是否是当前给定问题的良好解决方案时,有一…...
Git笔记--Ubuntu上传本地项目到github
目录 1--基本配置 2--本地上传 1--基本配置 ① 创建ssh-key cd ~/.sshssh-keygen -t rsa -C "邮箱地址"② 查看并关联ssh-key gedit id_rsa.pub 复制内容,在 GitHub 中依次点击 Settings -> SSH and GPG keys -> New SSH key,将 id…...

基于Go编写一个可视化Navicat本地密码解析器
前提 开发小组在测试环境基于docker构建和迁移一个MySQL8.x实例,过程中大意没有记录对应的用户密码,然后发现某开发同事本地Navicat记录了根用户,于是搜索是否能够反解析Navicat中的密码掩码(这里可以基本断定Navicat对密码是采用…...

Maven【入门笔记】
Maven 解决版本依赖的问题 https://www.liaoxuefeng.com/wiki/1252599548343744/1309301146648610 如果没有项目管理工具,在开发项目的时候,我们需要手动管理依赖包,需要管理依赖包的版本、去找到并下载依赖包、还有依赖包所依赖的包 等等。…...
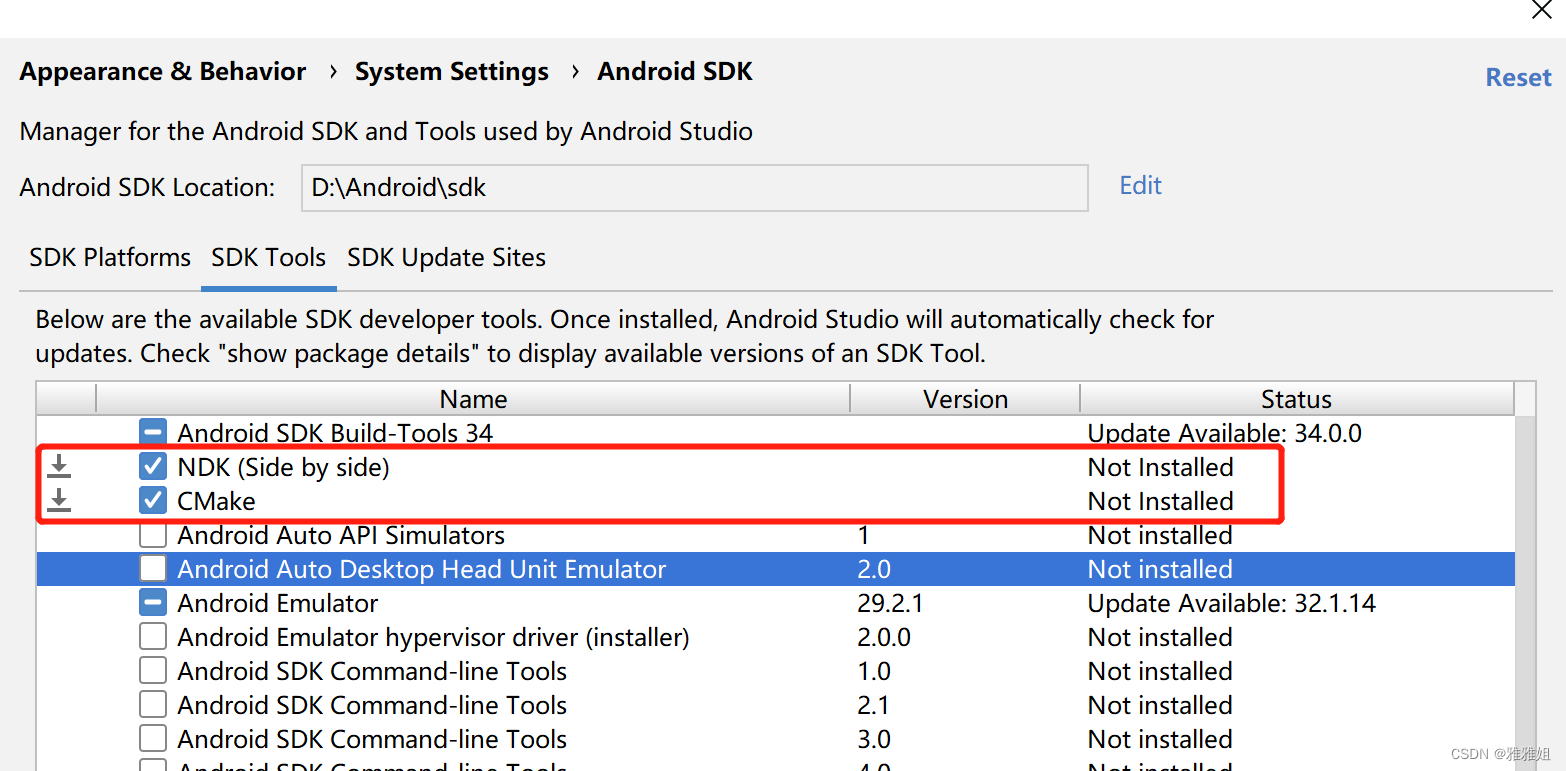
Android Studio中使用cmake开发JNI实战
JNI学习大纲 一、JNI编程入门 二、Android Studio中使用cmake开发JNI实战 第一章节我们介绍了JNI的开发步骤,那这一章节我们就开始在Android Studio中实战一下吧,Lets Start。 1. Android Studio中安装CMake插件 AS中菜单栏选择Tools>SDK Manager在…...
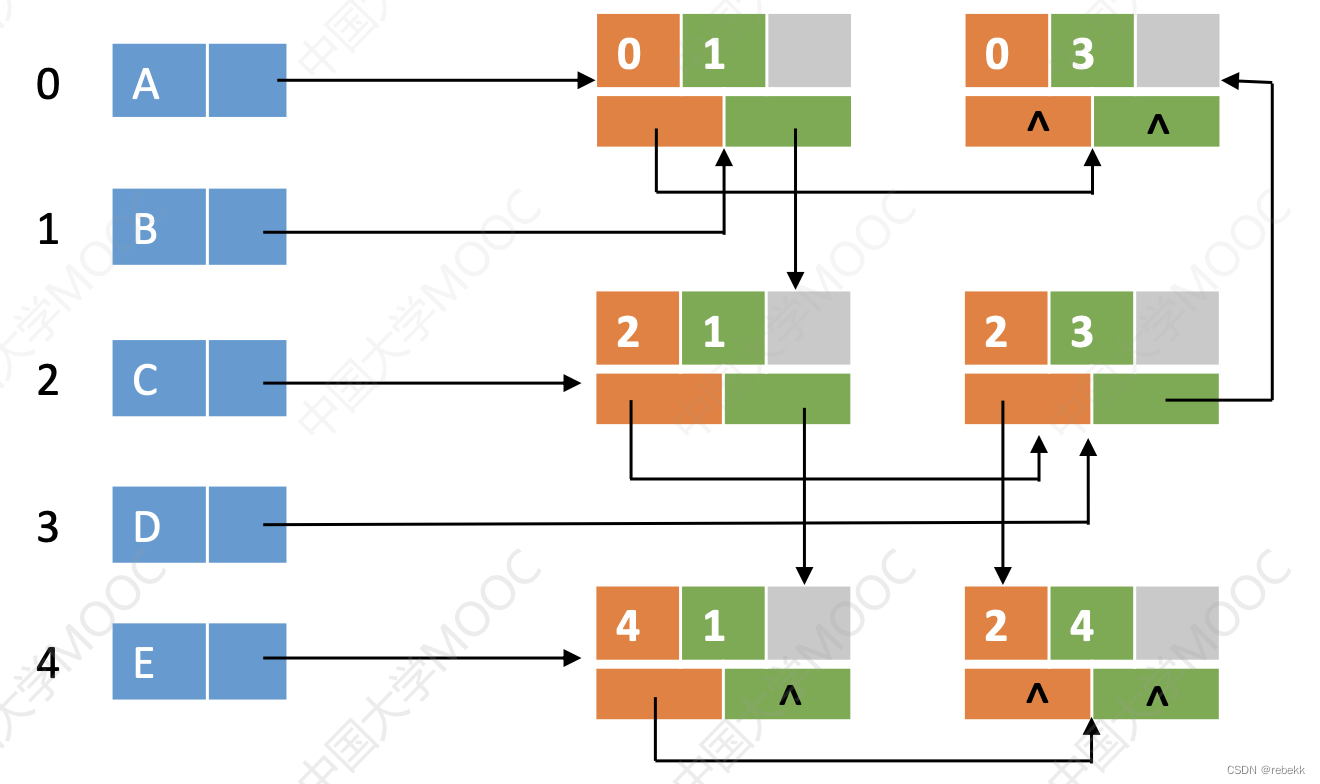
第七章 图论
第七章 图论 一、数据结构定义 图的邻接矩阵存储法#define MaxVertexNum 100 // 节点数目的最大值// 无边权,只用0或1表示边是否存在 bool graph[MaxVertexNum][MaxVertexNum];// 有边权 int graph[MaxVertexNum][MaxVertexNum];图的邻接表存储法 把所有节点存储为…...
)
IEEE SystemVerilog Chapter13 : Tasks and functions (subroutines)
13.2 Overview 任务和函数提供了从描述中的几个不同位置执行通用过程的能力。它们还提供了一种将大型过程分解为小型过程的方法,以便更容易地阅读和调试源代码描述。本小节讨论了任务和函数之间的区别,描述了如何定义和调用任务和函数,并给出…...
day39反转字符串总结
反转字符串原理其实就是交换位置,以中间为分隔点; 基本套路:遍历前一般字符,互换位置; for循环模板 void reverseString(char* s, int sSize){char temp;for (int i 0, j sSize - 1; i < sSize/2; i, j--) {temp…...
使用Socket实现TCP版的回显服务器
文章目录 1. Socket简介2. ServerSocket3. Socket4. 服务器端代码5. 客户端代码 1. Socket简介 Socket(Java套接字)是Java编程语言提供的一组类和接口,用于实现网络通信。它基于Socket编程接口,提供了一种简单而强大的方式来实现…...
【Nacos篇】Nacos基本操作及配置
官方文档:https://nacos.io/zh-cn/docs/v2/ecology/use-nacos-with-spring-cloud.html 前置条件:SpringCloud脚手架 单机模式下的Nacos控制台: <dependencies><!-- Registry 注册中心相关 --><dependency><groupId>…...
Dockerfile构建Tomcat镜像
准备apache包和jdk并解压 [rootlocalhost tomcat]# ll 总用量 196728 -rw-r--r--. 1 root root 9690027 7月 17 2020 apache-tomcat-8.5.40.tar.gz -rw-r--r--. 1 root root 674 8月 2 20:19 Dockerfile -rw-r--r--. 1 root root 191753373 7月 17 2020 jdk-8u191-…...

k8s的介绍
简介 Kubernetes,简称K8s,是用8代替名字中间的8个字符“ubernete”而成的缩写。是一个开源的,用于管理云平台中多个主机上的容器化的应用, K8s的目标是让部署容器化的应用简单并且高效,K8s提供了应用部署,规划,更新,维护的一种机制。 K8s是Google开源的一个容器编排引…...

mysql sql语句 需要使用like 场景,解决方案
mysql 多重like 解决方案 方案一、使用like 方案二、使用REGEXP 正则匹配 方案三、使用group_concat多重模糊匹配 方案一、使用like 查询user包含小李并且小王的相关数据 SELECT * FROM user WHERE name LIKE %小王% or name like %小王% 方案二、使用REGEXP 正则匹配 查询use…...
通过C语言设计的贪吃蛇游戏(控制台终端)
一、项目介绍 当前通过控制台终端实现一个贪吃蛇小游戏,实现游戏的绘制、更新、控制等功能。 二、实现效果 三、完整代码 下面贴出的代码在Windows系统上编译运行,需要使用conio.h头文件中的getch()函数来获取键盘输入,用于控制蛇的移动。…...
c++实现Qt信号和槽机制
文章目录 简介信号槽信号与槽的连接 特点观察者模式定义观察者模式结构图 实现简单的信号和槽 简介 信号槽机制与Windows下消息机制类似,消息机制是基于回调函数,Qt中用信号与槽来代替函数指针,使程序更安全简洁。 信号和槽机制是 Qt 的核心…...
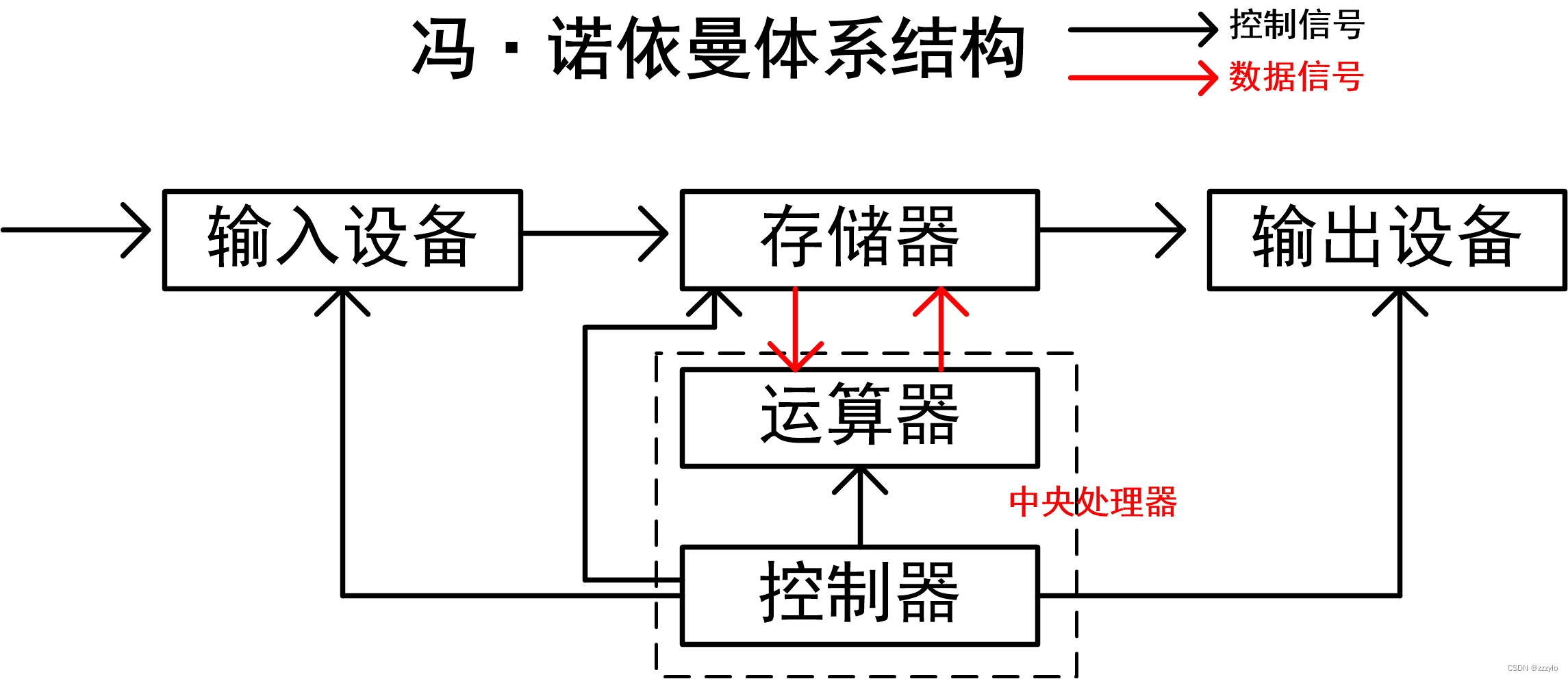
【Linux】五、进程
一、冯诺依曼体系结构 存储器:指的是内存; 输入设备:键盘、摄像头、话筒,磁盘,网卡; 输出设备:显示器、音响、磁盘、网卡; 中央处理器(CPU):运算器…...
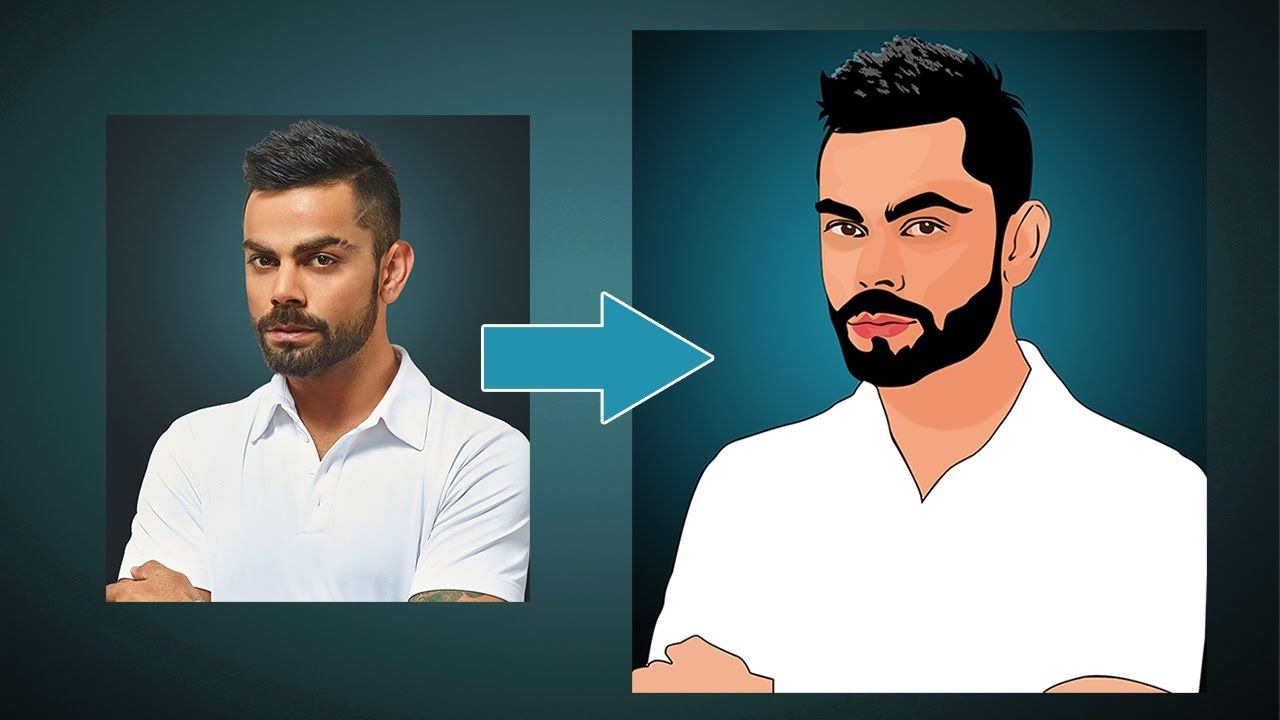
使用 OpenCV 和 Python 卡通化图像-附源码
介绍 在本文中,我们将构建一个有趣的应用程序,它将卡通化提供给它的图像。为了构建这个卡通化器应用程序,我们将使用 python 和 OpenCV。这是机器学习令人兴奋的应用之一。在构建此应用程序时,我们还将了解如何使用 easygui、Tkinter 等库。在这里,您必须选择图像,然后应…...

GitLab不同角色对应的权限
Owner(拥有者): 拥有者是项目或组的创建者,拥有最高级别的权限。他们可以添加、删除项目成员,修改项目设置,管理访问权限,并进行项目转让。在组级别,他们还可以添加或删除子组和项目…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
