LeetCode 42. 接雨水(动态规划 / 单调栈)
题目:
链接:LeetCode 42. 接雨水
难度:困难
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
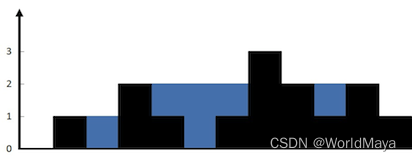
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
- n == height.length
- 1 <= n <= 2 * 104
- 0 <= height[i] <= 105
方法一:
动态规划:
按列求每一列能存的雨水时,应该求这一列左右最高的墙,其中较矮的墙与这一列高度的差值(>0)为当前列能存的雨水量。对于求左右最高的墙,我们可以用动态规划的方法做:
首先用两个数组,max_left [i] 代表第 i 列左边最高的墙的高度,max_right[i] 代表第 i 列右边最高的墙的高度。(一定要注意下,第 i 列左(右)边最高的墙,是不包括自身的)
对于 max_left我们其实可以这样求。
max_left [i] = Max(max_left [i-1],height[i-1])。它前边的墙的左边的最高高度和它前边的墙的高度选一个较大的,就是当前列左边最高的墙了。
对于 max_right我们可以这样求。
max_right[i] = Max(max_right[i+1],height[i+1]) 。它后边的墙的右边的最高高度和它后边的墙的高度选一个较大的,就是当前列右边最高的墙了。
得到了左右最高墙的结果,我们再用前面提到的方法按列求雨水量即可。
代码一:
class Solution {
public:int trap(vector<int>& height) {int n = height.size();int maxleft[n], maxright[n];maxleft[0] = 0, maxright[n - 1] = 0;for(int i = 1; i < n; i++){maxleft[i] = max(maxleft[i - 1], height[i - 1]);}for(int i = n - 2; i >= 0; i--){maxright[i] = max(maxright[i + 1], height[i + 1]);}int sum = 0;for(int i = 1; i < n - 1; i++){int num = min(maxleft[i], maxright[i]) - height[i];if(num > 0) sum += num;}return sum;}
};
时间复杂度O(N)。
空间复杂度O(N)。
方法二:
单调栈:
除了计算并存储每个位置两边的最大高度以外,也可以用单调栈计算能接的雨水总量。
维护一个单调栈,单调栈存储的是下标,满足从栈底到栈顶的下标对应的数组 height 中的元素递减。
从左到右遍历数组,遍历到下标 iii 时,如果栈内至少有两个元素,记栈顶元素为 top,top 的下面一个元素是 left,则一定有 height[left] ≥ height[top]。如果 height[i] > height[top],则得到一个可以接雨水的区域,该区域的宽度是 i−left−1,高度是 min(height[left], height[i]) − height[top],根据宽度和高度即可计算得到该区域能接的雨水量。
为了得到 left,需要将 top 出栈。在对 top 计算能接的雨水量之后,left 变成新的 top,重复上述操作,直到栈变为空,或者栈顶下标对应的 height 中的元素大于或等于 height[i]。
在对下标 i 处计算能接的雨水量之后,将 i 入栈,继续遍历后面的下标,计算能接的雨水量。遍历结束之后即可得到能接的雨水总量。
代码二:
class Solution {
public:int trap(vector<int>& height) {int n = height.size();stack<int> s; // 单调栈int sum = 0;for(int i = 0; i < n; i++){while(!s.empty() && height[i] > height[s.top()]) {int bottom = height[s.top()];s.pop();int left, left_i;if(s.empty()) {left = 0;left_i = 0;}else {left = height[s.top()];left_i = s.top();}int wallHeight = min(left, height[i]);int num = (wallHeight - bottom) * (i - left_i - 1);if(num > 0) sum += num;}s.emplace(i);}return sum;}
};
时间复杂度O(N),N是数组 height 长度,每个元素只会入栈和出栈一次。
空间复杂度O(N),栈空间最多为N。
相关文章:

LeetCode 42. 接雨水(动态规划 / 单调栈)
题目: 链接:LeetCode 42. 接雨水 难度:困难 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2…...

顺序表、链表刷题指南(力扣OJ)
目录 前言 题目一:删除有序数组中的重复项 思路: 题解: 题目二:合并两个有序数组 思路: 分析: 题解: 题目三:反转链表 思路: 分析: 题解: 题目四&…...

Lambda表达式总结
Lambda作为Java8的新特性,本篇文章主要想总结一下常用的一下用法和api 1.接口内默认方法实现 public interface Formula {double calculate(int a);// 默认方法default double sqrt(int a) {return Math.sqrt(a);} }public static void main(String[] args) {Form…...

岛屿的最大面积
给你一个大小为 m x n 的二进制矩阵 grid 。 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。 岛屿的面积是岛上值为 1 …...
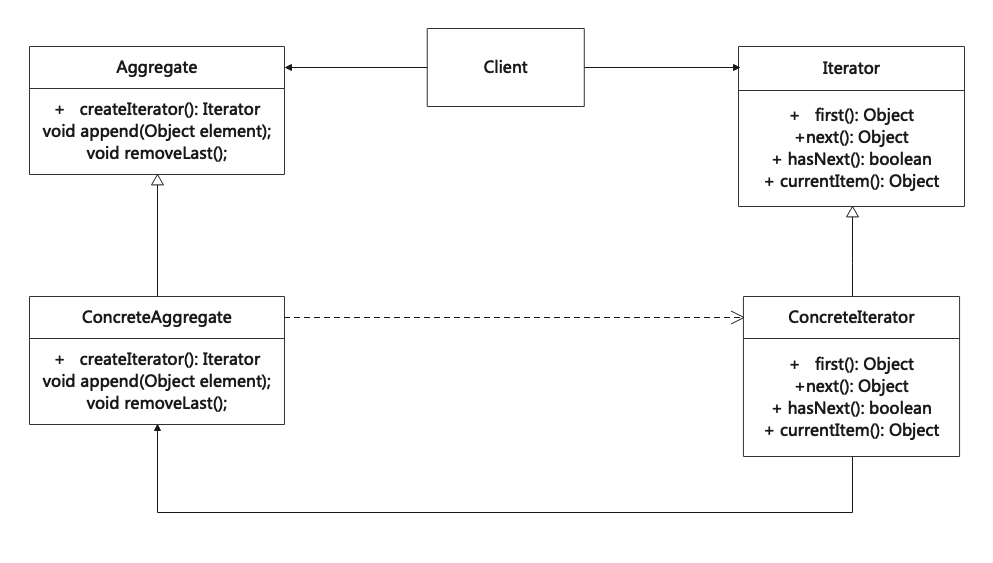
迭代器模式(Iterator)
迭代器模式是一种行为设计模式,可以在不暴露底层实现(列表、栈或树等)的情况下,遍历一个聚合对象中所有的元素。 Iterator is a behavior design pattern that can traverse all elements of an aggregate object without exposing the internal imple…...
Goland搭建远程Linux开发
Windows和Linux都需要先构建好go环境,启用ssh服务。 打开Windows上的Goland,建立项目。 点击添加配置,选择go构建 点击运行于,选择ssh 填上Linux机器的IP地址和用户名 输入密码 没有问题 为了不让每次运行程序和调试程序都生…...

react中PureComponent的理解与使用
一、作用 它是一个纯组件,会做一个数据的浅比较,当props和state没改变的时候,不会render重新渲染, 改变后才会render重新渲染,提高性能。 二、使用 三、注意 它不能和shouldComponentUpdate生命周期同时使用。因为它…...

洛谷——P5714 【深基3.例7】肥胖问题
文章目录 题目题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 样例 #2样例输入 #2样例输出 #2 提示 AC代码 题目 题目描述 BMI 指数是国际上常用的衡量人体胖瘦程度的一个标准,其算法是 m h 2 \dfrac{m}{h^2} h2m,其中 m m m 是指体重&am…...

Mac隐藏和显示文件
由于之前没有使用过Mac本,所以很多地方都不太清楚,在下载git项目的时候,发现没有.git文件, 一开始还以为下载错了,但是git命令是可以看到远端分支以及当前分支的,之后在一次解压文件的时候发现,…...

软件工程中应用的几种图辨析
【软件工程】软件工程中应用的几种图辨析:系统流程图、数据流图、数据字典、实体联系图、状态转换图、层次方框图、Warnier图、IPO图、层次图、HIPO图、结构图、程序流程图、盒图、PAD图、判定表_眩晕李的博客-CSDN博客 软件工程——实体关系图 状态转换图 数据流…...
下载离线版的VS Visual Studio 并下载指定的版本
一、先下载引导程序 下载地址VS VisualStudio官网 在这个页面翻到最下面 在这里下载需要的版本 下载引导程序 二、下载离线安装包 写一个批处理文件(vs.bat) 命令格式如下 <vs引导程序exe> --layout <离线安装包下载的路径> --add <功能…...
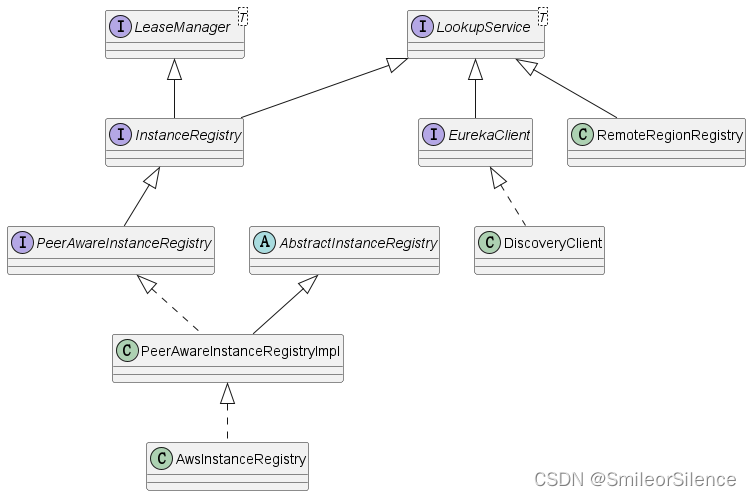
Eureka 学习笔记5:InstanceRegistry
版本 awsVersion ‘1.11.277’ LeaseManager 接口管理实例的租约信息,提供以下功能: 注册实例取消注册实例实例续约剔除过期实例 public interface LeaseManager<T> {/** 注册实例并续约*/void register(T r, int leaseDuration, boolean isRep…...
System Verilog——虚方法的使用
1、使用虚方法目的 通过在父类里定义虚方法(task or function),可以在当父类句柄调用一个方法时候,前提是若是这个句柄指向了子类对象,则调用的方法为子类的方法而不是父类的方法。 1.1、实例理解:将子类句柄赋值成父类句柄 mod…...

线性规划和单纯形法-原理篇
文章目录 引言线性规划标准型问题特点单纯形法 引言 很多运筹学的教材都是从线性规划开始的,我平时做算法策略的落地应用时也研发了一部分基于线性规划的技术方案。可以说,如果搞不懂线性规划,很难成为一名优秀的运筹优化算法工程师。 但是…...

FBX SDK开发快速上手指南
一段时间以来,我一直想制作一个 FBX Exporter 将 FBX 文件转换为我自己的格式。 整个过程不是很顺利,主要是FBX的官方文档不是很清楚。 另外,由于 FBX 格式被许多应用程序使用,而不仅仅是游戏引擎,因此提供的示例代码没…...

探讨|使用或不使用机器学习
动动发财的小手,点个赞吧! 机器学习擅长解决某些复杂问题,通常涉及特征和结果之间的困难关系,这些关系不能轻易地硬编码为启发式或 if-else 语句。然而,在决定 ML 是否是当前给定问题的良好解决方案时,有一…...
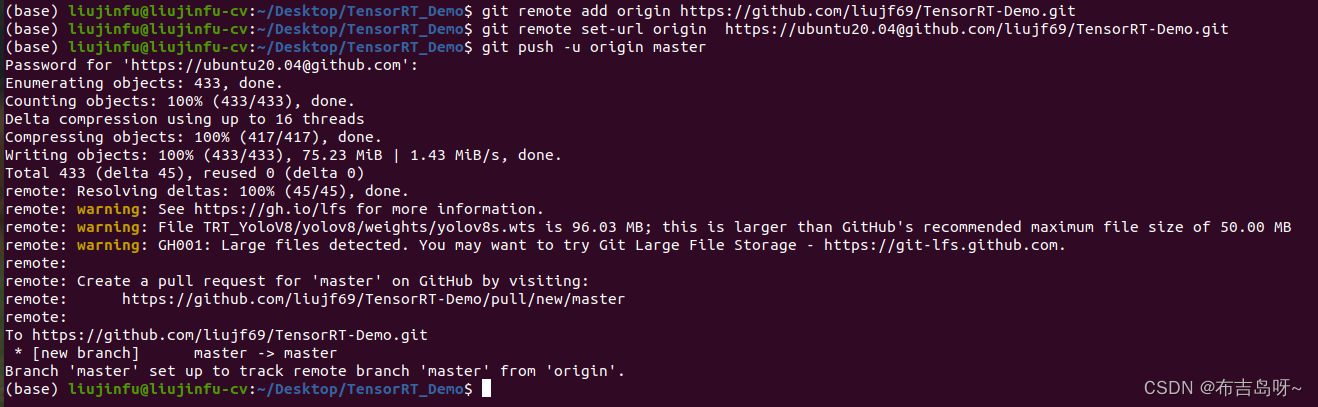
Git笔记--Ubuntu上传本地项目到github
目录 1--基本配置 2--本地上传 1--基本配置 ① 创建ssh-key cd ~/.sshssh-keygen -t rsa -C "邮箱地址"② 查看并关联ssh-key gedit id_rsa.pub 复制内容,在 GitHub 中依次点击 Settings -> SSH and GPG keys -> New SSH key,将 id…...

基于Go编写一个可视化Navicat本地密码解析器
前提 开发小组在测试环境基于docker构建和迁移一个MySQL8.x实例,过程中大意没有记录对应的用户密码,然后发现某开发同事本地Navicat记录了根用户,于是搜索是否能够反解析Navicat中的密码掩码(这里可以基本断定Navicat对密码是采用…...

Maven【入门笔记】
Maven 解决版本依赖的问题 https://www.liaoxuefeng.com/wiki/1252599548343744/1309301146648610 如果没有项目管理工具,在开发项目的时候,我们需要手动管理依赖包,需要管理依赖包的版本、去找到并下载依赖包、还有依赖包所依赖的包 等等。…...
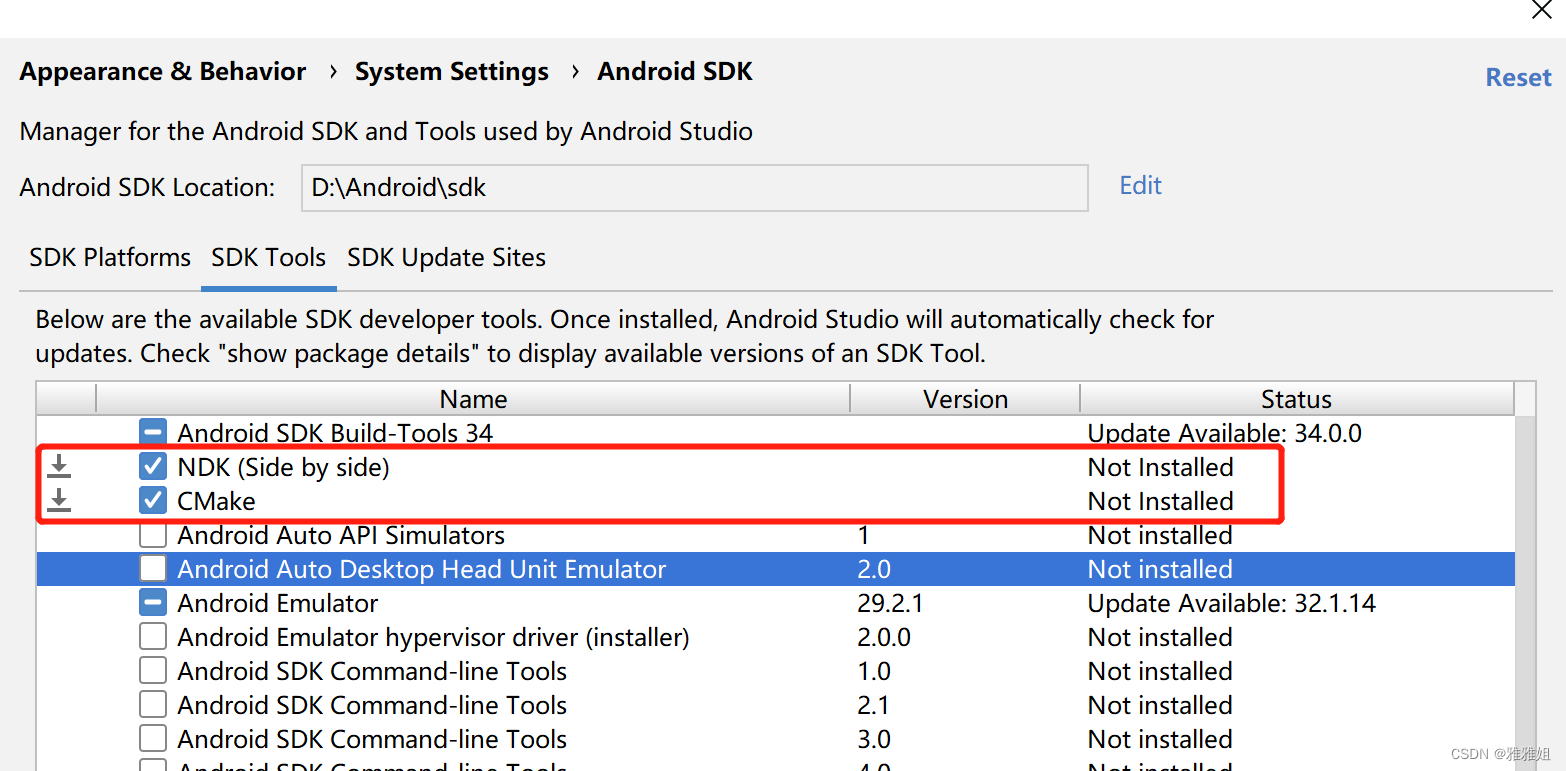
Android Studio中使用cmake开发JNI实战
JNI学习大纲 一、JNI编程入门 二、Android Studio中使用cmake开发JNI实战 第一章节我们介绍了JNI的开发步骤,那这一章节我们就开始在Android Studio中实战一下吧,Lets Start。 1. Android Studio中安装CMake插件 AS中菜单栏选择Tools>SDK Manager在…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
