【数模】奇异值分解SVD和图形处理
- 介绍奇异值分解在图形压缩中的运用,并将简单介绍下Matlab对于图形和视频的处理
一、奇异值分解介绍
1.1 基本概念
- 奇异值分解(Singular Value Decomposition,以下简称SVD)是线性代数中一种重要的矩阵分解:
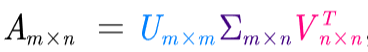
- U和V都是正交矩阵
- ∑是奇异值矩阵(和A的大小相同,其主对角元素是从大到小排列的,这些对角元素称为奇异值,其他位置元素为0)

1.2 求∑的步骤
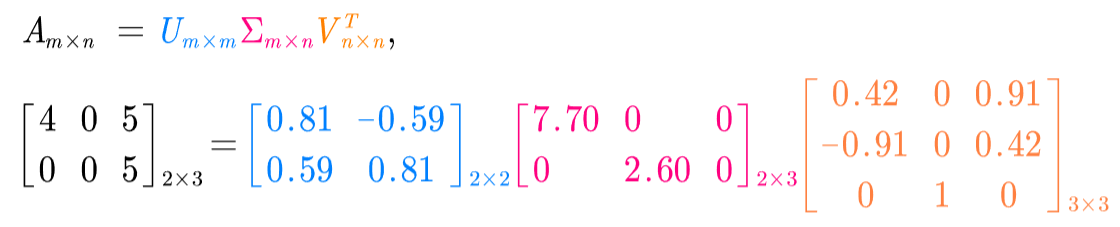
1.2.1 U的计算

1.2.2 V的计算

1.2.3 ∑的计算

1.3 利用SVD对数据进行"降维"
- 举例:

- 此处的“降维”:更准确而言是使得矩阵的秩减小,矩阵大小并未改变。
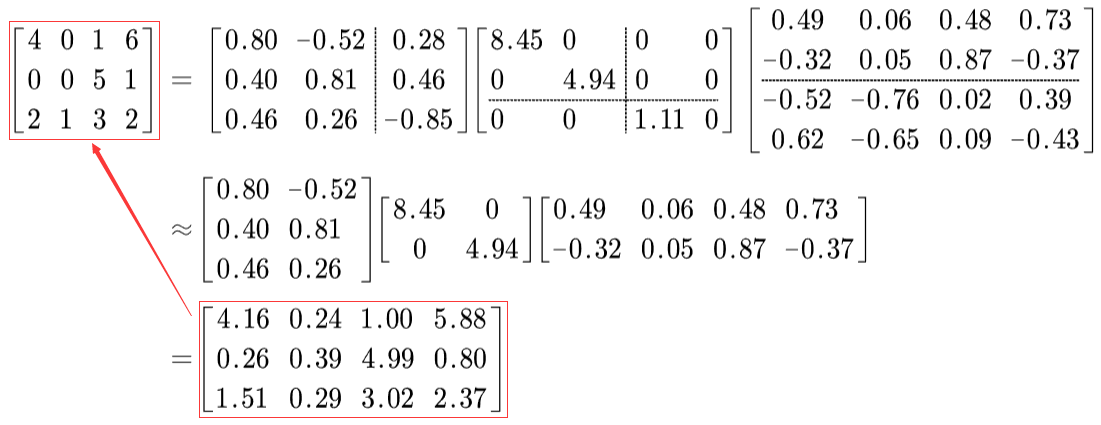
- 保留原矩阵的特征比例
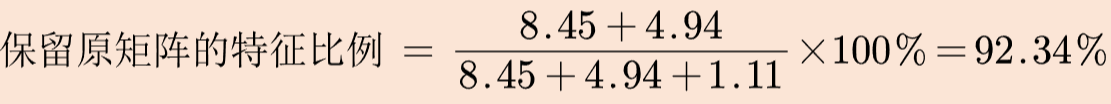
二、Matlab对奇异值分解
- 矩阵压缩
2.1 Matlab自带分解:[U,S,V] = svd(A)

% PPT_example.m文件
A = [4 0 1 6;0 0 5 1;2 1 3 2] % A : 3*4
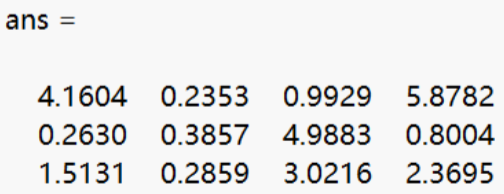
[U,S,V] = svd(A)
% 注意:U*S*(V的转置) == A
% U:3*3 S:3*4 V : 4*4
U*S*V' - A
% 因为浮点数计算的缘故,所以会有非常微小的偏差
% 1.0e-14 * 0.2665 = 0.000000000000002665
U(:,1:2)*S(1:2,1:2)*V(:,1:2)'
U(:,1:3)*S(1:3,1:3)*V(:,1:3)' % 就是A
2.2 自定义的mysvd函数
- 取自清风老师自定义的,不同于Matlab自带的:使用奇异值分解将矩阵A压缩到指定的特征比例
% mysvd.m文件
function [compress_A] = mysvd(A, ratio)
% 输入变量% A:要压缩的m*n维的矩阵% ratio:(至少)要保留原矩阵的特征比例(100%表示不压缩)
% 输出变量% compress_A:压缩后的矩阵

三、Matlab图形的处理
- 图片压缩
3.1 RGB模式
- RGB色彩(三原色):R代表Red(红色),G代表Green(绿色),B代表Blue(蓝色)。
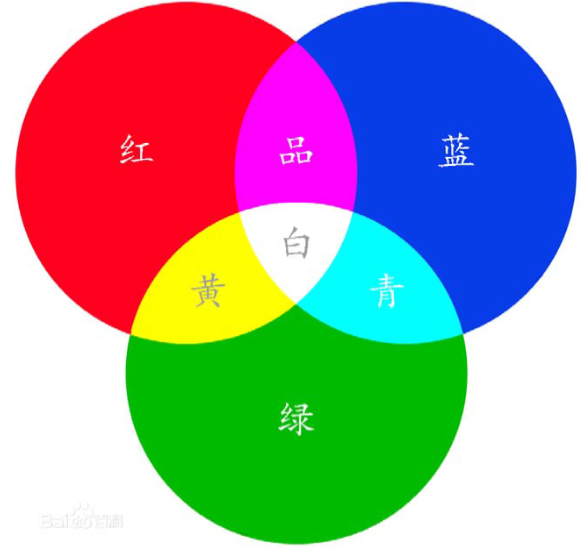
- 计算机定义颜色时R、G、 B三种成分的取值范围是0‐255,0表示没有刺激量,255表示刺激量达最大值。
- R、G、B均为255时就合成了白光,R、G、B均为0时就形成了黑色。
- 灰色图片:R、G、B三原色完全相同;否则称为彩色图片。
3.2 图片压缩的函数
- 函数作用:利用SVD函数对图形进行压缩
- 输入变量
- photo_address:要压缩的图片存放的位置(建议输入完整的路径)
- save_address:将压缩后的图片保存的位置(建议输入完整的路径)
- ratio:要保留原矩阵的特征比例(100%表示不压缩)
- greycompress: 如果该值等于1,则会彩色的原图片转换为灰色图片后再压缩;默认值为0,表示不进行转换
- 输出变量:无(不需要输出,因为函数运行过程中已经将图片保存了)
% photo_compress.m文件
function []= photo_compress(photo_address, save_address,
ratio, greycompress)
3.3 SVD压缩后的效果


四、视频分离为图片
4.1 video2photo.m代码文件
- Matlab对视频的要求较高,有的原视频属性详细情况不带帧数,可以采用转化器转个视频格式(如迅捷视频转换器),否则可能会报如下错误:
- 错误使用 VideoReader/init (line 619)
- 无法确定所需的编解码器
- video中的对象讲解
%% 读取视频
video_file='迅捷视频转换器转换后的新闻联播.mp4';
video=VideoReader(video_file);
frame_number = video.NumberOfFrames; %视频的总帧数%% 分离图片
for i=1:30:frame_number % 这里演示的是每30帧数保存一次(如果每一帧都全部保存的话所要花费的时间很长)image_name=strcat('C:\Users\hc_lzp\Desktop\数学建模视频录制\第13讲.奇异值分解\代码和例题数据\将视频转成图片\图片\image_',num2str(i),'.jpg');Photo=read(video,i); %读出所在帧的图片对象imwrite(Photo,image_name); %将图片保存到指定的位置
end
4.2 分离效果
4.3 批量处理文件夹内的所有图片

folder_name = 'C:\Users\hc_lzp\Desktop\数学建模视频录制\第13讲.奇异值分解\代码和例题数据\压缩文件夹内的所有图片\葫芦娃七兄弟';
dirOutput=dir(fullfile(folder_name, '*.jpg'));
files={dirOutput.name};
n = length(files);
ratio = 0.9;
for i = 1:nphotoname = files(i);name = photoname{1};photo_address = fullfile(folder_name, name);disp(photo_address)save_address = fullfile(folder_name, strcat('compress_',name));photo_compress(photo_address, save_address, ratio)
end
五、SVD的评价和应用
5.1 SVD(奇异值分解)评价
- 优点:简化数据,去除噪声点,对数据降维(减少秩);
- 缺点:数据的转换可能难以理解;
- 适用于数据类型:数值型。
- 通过SVD对数据的处理,可对原始数据进行精简,实际上是去除了噪声和冗余信息,以此达到了优化数据的目的。
5.2 SVD的另外两个重要应用
- 潜在语义索引:最早的SVD应用之一就是信息检索,称利用SVD的方法为潜在语义检索(LSI)或隐形语义分析(LSA)
- 有兴趣可以去阅读吴军老师的《数学之美》。
- 推荐系统:SVD的另一个应用就是推荐系统,较为先进的推荐系统先利用SVD从数据中构建一个主题空间,然后再在该空间下计算相似度,以此提高推荐的效果。
相关文章:

【数模】奇异值分解SVD和图形处理
介绍奇异值分解在图形压缩中的运用,并将简单介绍下Matlab对于图形和视频的处理 一、奇异值分解介绍 1.1 基本概念 奇异值分解(Singular Value Decomposition,以下简称SVD)是线性代数中一种重要的矩阵分解: U和V都是正交矩阵∑是奇异值矩阵&…...
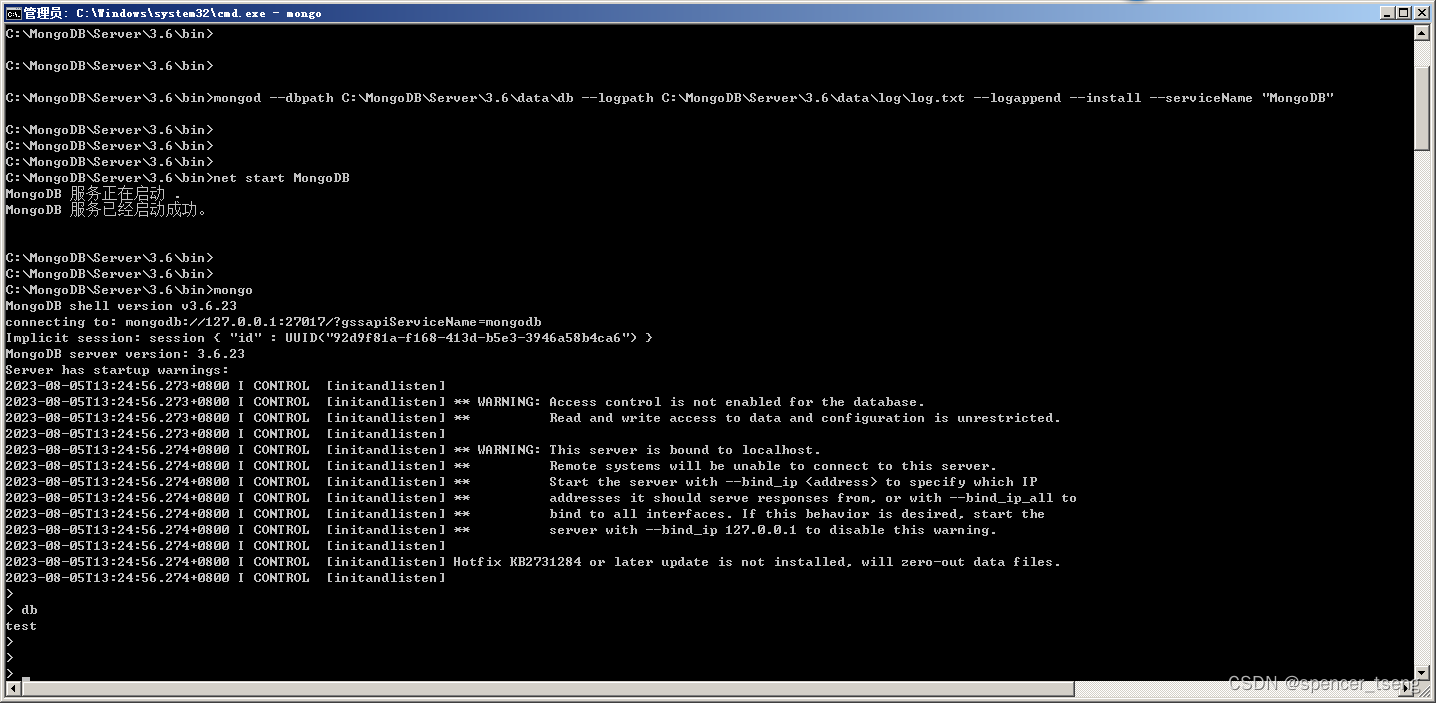
mongodb-win32-x86_64-2008plus-ssl-3.6.23-signed.msi
Microsoft Windows [版本 6.1.7601] 版权所有 (c) 2009 Microsoft Corporation。保留所有权利。C:\Users\Administrator>cd C:\MongoDB\Server\3.6\binC:\MongoDB\Server\3.6\bin> C:\MongoDB\Server\3.6\bin> C:\MongoDB\Server\3.6\bin>mongod --dbpath C:\Mongo…...

华为Euler系统忘记密码之密码重置
目录 1. 进入GRUB引导菜单编辑模式2. 指定系统在启动时使用/bin/sh作为初始化进程3. 修改密码3.1 重新挂载文件系统,使文件系统可写3.2 修改密码3.3 重新标记文件的安全上下文 4. 开机输入修改的密码正常登录 1. 进入GRUB引导菜单编辑模式 启动openEuler࿰…...

Java-多线程-深入理解ConcurrentHashMap
目录 什么是ConcurrentHashMap?为什么有ConcurrentHashMap?和HashMap区别示例代码对比 JDK7和JDK8中ConcurrentHashMap整体架构的区别JDK7中JDK8中 ConcurrentHashMap的基本功能在性能方面的优化使用到的技术-CAS概念说明比较并交换的过程如下࿱…...
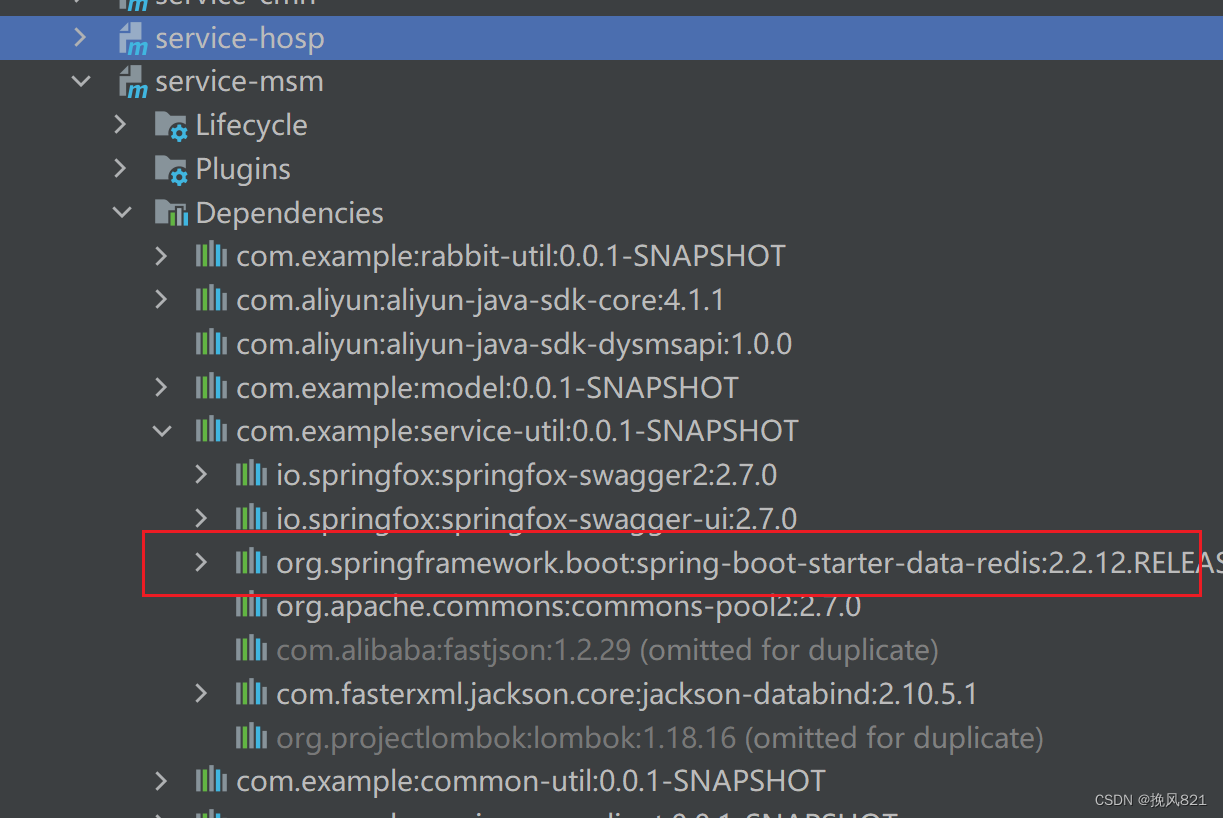
没有配置redis但是报错连接redis失败
问题 没有配置redis但是报错连接redis失败 检查maven配置是否引入了redis依赖(可能是传递依赖,最好检查引进来的公共工程 解决办法 只需要在该工程application.yml文件中配置一下 redis就好,或者移除redis依赖 spring:redis:password: hos…...

剑指 Offer 04. 二维数组中的查找
力扣 在一个 n * m 的二维数组中,每一行都按照从左到右 非递减 的顺序排序,每一列都按照从上到下 非递减 的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。 示例: 现有矩阵 matrix…...

【工作中问题解决实践 九】Spring中事务传播的问题排查
最近在工作中遇到了两个关于事务操作的问题,顺便就着这两个问题又回顾了一遍Spring的事务相关的操作,想着一次性把这个问题研究明白了,后续使用事务的时候也能踏实点,让事务发挥真实的作用 什么是事务?什么是事务管理…...

【导出Word】如何使用Java+Freemarker模板引擎,根据XML模板文件生成Word文档(只含文本内容的模板)
这篇文章,主要介绍如何使用JavaFreemarker模板引擎,根据XML模板文件生成Word文档。 目录 一、导出Word文档 1.1、基础知识 1.2、制作模板文件 1.3、代码实现 (1)引入依赖 (2)创建Freemarker工具类 &…...
Devart dbForge Studio for MySQL Crack
Devart dbForge Studio for MySQL Crack dbForge Studio for MySQL是一个用于MySQL和MariaDB数据库开发、管理和管理的通用GUI工具。IDE允许您通过直观的界面创建和执行查询、开发和调试存储例程、自动化数据库对象管理、分析表数据。MySQL客户端提供了数据和模式比较和同步工具…...

C++、Java、JavaScript和python几个语句的对比介绍
C、Java、JavaScript和python几个语句的对比介绍 C、Java、JavaScript和python语言的for语句 C、Java和JavaScript的for语句的语法类似如下: for (初始条件; 循环条件; 循环后操作) { // 循环体代码 } 初始条件是在进入循环之前执行的语句,初始化循环…...

第20节 R语言医学分析:某保险医疗事故赔偿因素分析
文章目录 某保险医疗事故赔偿因素分析源码源文件下载某保险医疗事故赔偿因素分析 我们分析数据集“诉讼”的第一个方法是确定样本数量、变量类型、缩放/编码约定(如果有)用于验证数据清理。 接下来,数据集看起来很干净,没有缺失值,并且对于分类变量,将编码约定替换为实际…...

【雕爷学编程】MicroPython动手做(28)——物联网之Yeelight 4
知识点:什么是掌控板? 掌控板是一块普及STEAM创客教育、人工智能教育、机器人编程教育的开源智能硬件。它集成ESP-32高性能双核芯片,支持WiFi和蓝牙双模通信,可作为物联网节点,实现物联网应用。同时掌控板上集成了OLED…...

解决K8S集群设置污点后,污点不生效,下发应用的问题
问题:在集群中部署了三个daemonset,一开始加了容忍Toleration,后边去掉Toleration后,还是一直往边缘节点上部署应用,非常离谱 解决:删掉Toleration后,需要把annotations一起删掉,因为…...

使用$test$plusargs提高RTL验收速度
文章目录 0 前言1 语法介绍2 示例3 多种情况的testbench怎么写 0 前言 这段时间在整合一个小ip,因为要验证每个feature是否可行,需要用testbench C语言的方式进行仿真验证,由于每种feature不仅要在C语言中修改寄存器配置,还要再…...
MySQL~mysql基础应用相关题
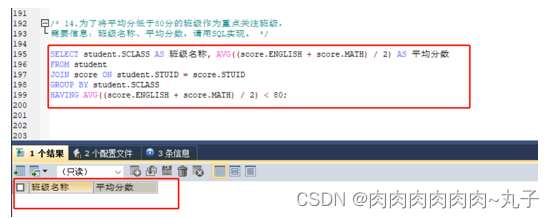
整卷阅览: 想要获取试卷原版请点击以下链接下载: https://download.csdn.net/download/qq_53142796/88168133https://download.csdn.net/download/qq_53142796/88168133 解题过程: 数据库:studentdb 数据库表如下: …...

Redis | 哨兵模式
Redis | 哨兵模式 1. 简介 Redis Sentinel(哨兵)是Redis提供的一种高可用性解决方案。它是一个独立的进程,用于监控和管理Redis主从模式的节点,并在主节点故障时自动进行故障转移。哨兵模式可以确保Redis集群的高可用性和数据一…...
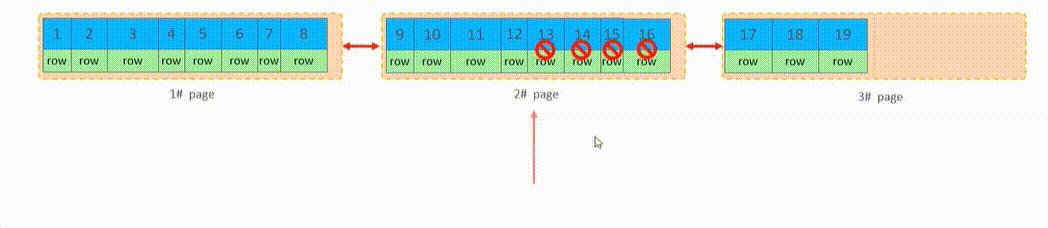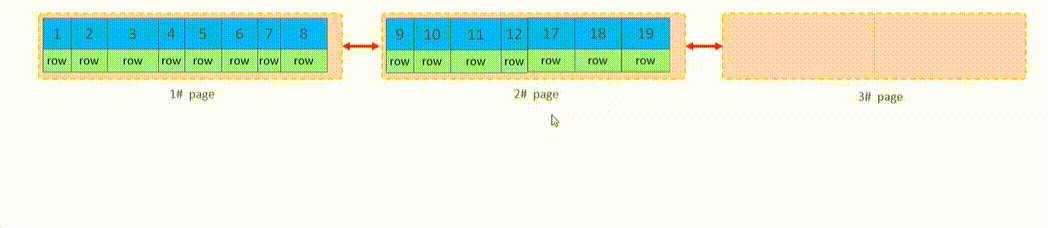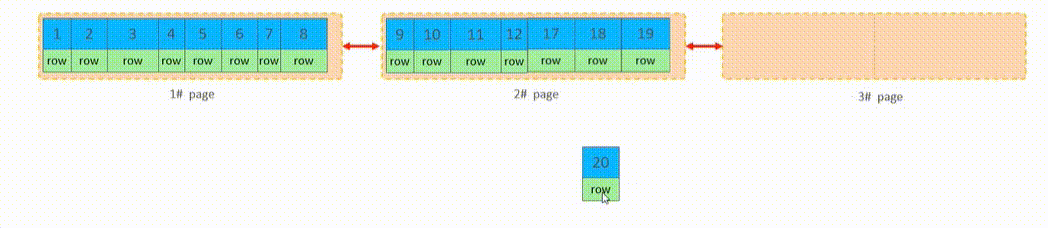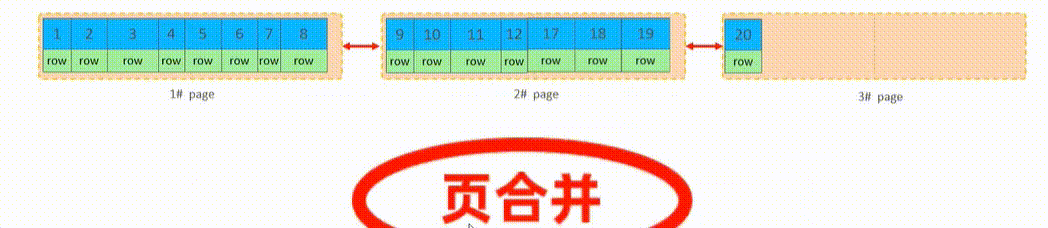
MySQL语句性能分析与优化
目录 SQL性能分析 SQL执行频率 SQL慢查询日志 Profile Explain SQL优化 插入数据的优化 主键优化 Order By优化 Group By优化 Limit 优化 Count 优化 Update 优化 多表连接查询优化 SQL性能分析 通过SQL性能分析来做SQL的优化,主要是优化SQL的查询语…...

SpringBoot实现数据库读写分离
SpringBoot实现数据库读写分离 参考博客https://blog.csdn.net/qq_31708899/article/details/121577253 实现原理:翻看AbstractRoutingDataSource源码我们可以看到其中的targetDataSource可以维护一组目标数据源(采用map数据结构),并且做了路由key与目标…...
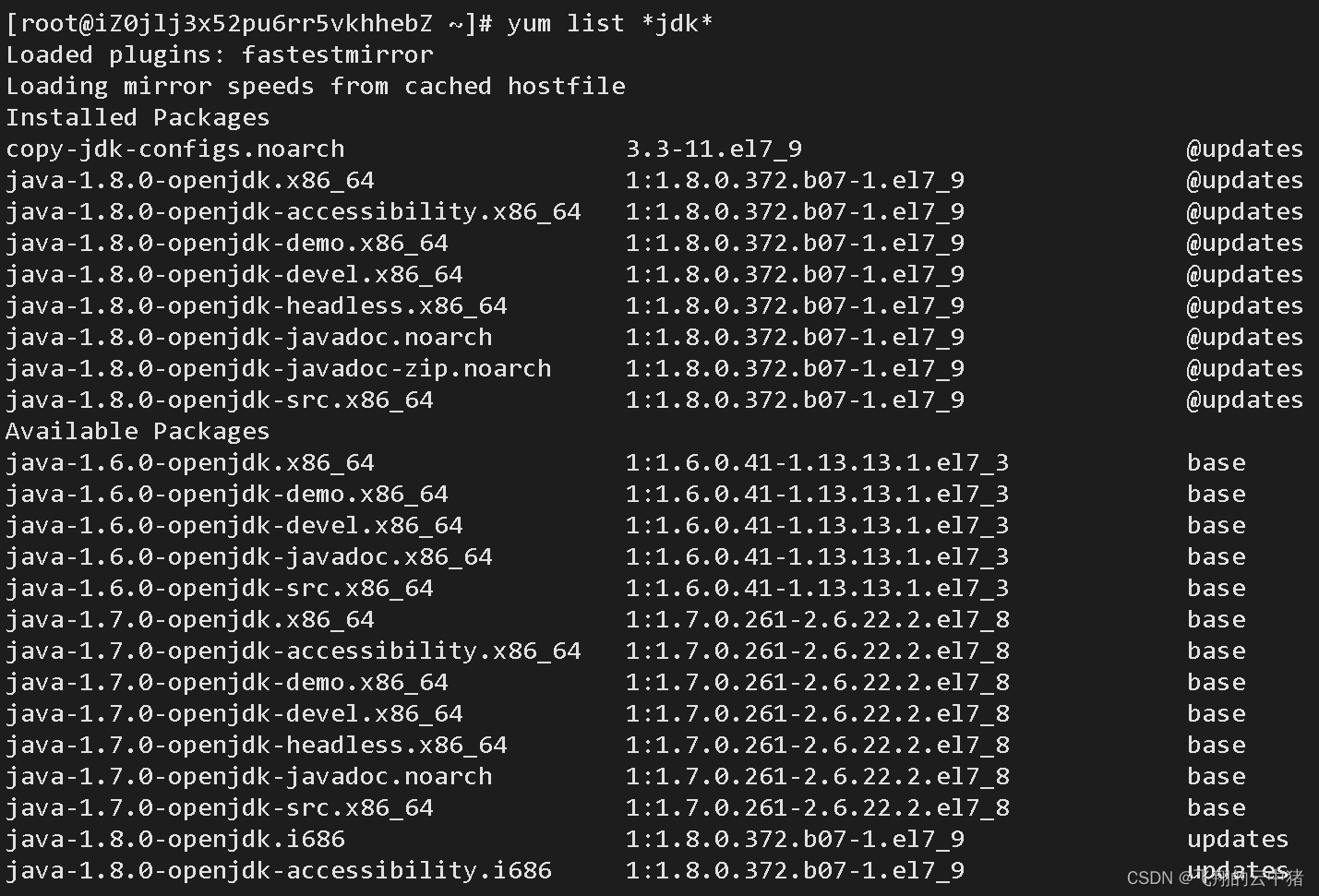
Linux(四)--包软件管理器与Linux上环境部署示例
一.包软件管理器【yum和apt】 1.先来学习使用yum命令。yum:RPM包软件管理器,用于自动化安装配置Linux软件,并可以自动解决依赖问题。通过yum命令我们可以轻松实现软件的下载,查找,卸载与更新等管理软件的操作。 最常用…...
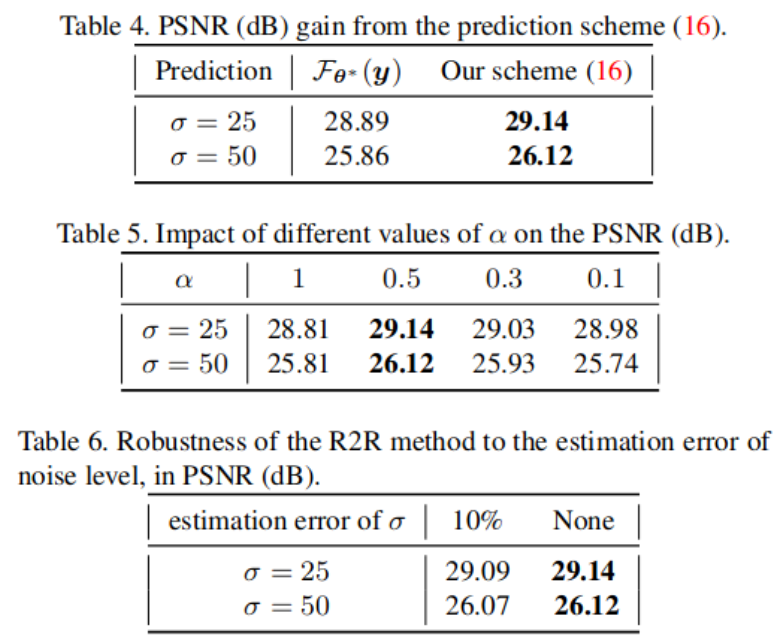
自监督去噪:Recorrupted-to-Recorrupted原理分析与总结
文章目录 1. 方法原理1.1 相关研究1.2 研究思路1.3 小结 2. 实验结果3. 总结 文章地址: https://ieeexplore.ieee.org/document/9577798/footnotes#footnotes 参考博客: https://github.com/PangTongyao/Recorrupted-to-Recorrupted-Unsupervised-Deep-Learning-for-Image-Den…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...
